Maths Olympiad Previous Year Paper -2 | Mathematics Olympiad for Class 9 PDF Download
| Table of contents |

|
| Logical Reasoning |

|
| Mathematical Reasoning |

|
| Everyday Mathematics |

|
| Achievers Section |

|
Note: The questions provided in this document are similar to the questions that were asked in the actual Olympiad exam. So, we recommend you study these for your Olympiad preparation
Logical Reasoning
Q1: Select a figure from the options which will continue the same series as established by the Problem Figures.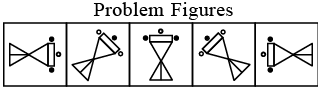 (a)
(a) 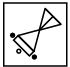
(b) 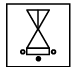
(c) 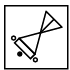
(d) 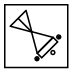
 View Answer
View Answer 
Ans: (c)
In each step, the figure rotates 45° anti-clockwise.
Also, shaded circles becomes unshaded and unshaded circle becomes shaded.
Q2: If ‘A’ is represented as ‘+’, ‘B’ as ‘–’, ‘C’ as ‘×’ and ‘D’ as ‘÷’, what is the result of 15A30D6C20B18?
(a) 99
(b) 115
(c) 104
(d) 97
 View Answer
View Answer 
Ans: (d)
- First, replace the letters with their corresponding operations: 15 + 30 ÷ 6 × 20 - 18.
- Next, follow the order of operations (BODMAS/BIDMAS): Start with division and multiplication from left to right.
- Calculate 30 ÷ 6 = 5, then 5 × 20 = 100.
- Now, the expression is 15 + 100 - 18, which equals 97.
Q3: There is a specific connection between the numbers on both sides of the ::. Determine the relationship of the provided pair and find the unknown number.
11 : 144 :: 14 : ?
(a) 225
(b) 169
(c) 196
(d) 256
 View Answer
View Answer 
Ans: (a)
- The relationship between the numbers is that the second number is the square of the first number plus a certain value.
- For the pair 11 : 144, we see that 11 squared is 121, and 121 plus 23 equals 144.
- Applying the same logic to 14, we calculate 14 squared, which is 196.
- Thus, the missing number is 14 squared minus 23, which gives us 225.
Q4: If the lengths of two diagonals of a rhombus are 18 cm and 24 cm, find the length of each side of the rhombus.
(a) 5 cm
(b) 10 cm
(c) 15 cm
(d) 25 cm
 View Answer
View Answer 
Ans: (c)
Length of each side of a rhombus = 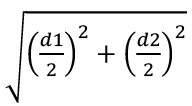
Length of each side of a rhombus = 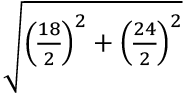
Length of each side of a rhombus = 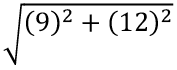
Length of each side of a rhombus = 15 cm
Q5: If the distance between the centres of two distant circles is 5 cm and the radius of the two circles are 6 cm and 3 cm, find the type of circles.
(a) Non-overlapping
(b) Touching externally
(c) Touching internally
(d) Intersecting
 View Answer
View Answer 
Ans: (d)
R + r > d > R - r
6 + 3 > 5 > 6 - 3
9 > 5 > 3
This condition is satisfying so the circles are intersecting.
Q6: In a cyclic quadrilateral PQRS, PS = PQ, RS = RQ and ∠PSQ = 2∠QSR. Find ∠QSR.
(a) 20º
(b) 40º
(c) 30º
(d) 50º
 View Answer
View Answer 
Ans: (c)
In a cyclic quadrilateral, opposite angles are supplementary.
Q7: Find the number of common tangents when the distance between the centres of the two circles is 7 cm and the radii are 5 cm and 2 cm.
(a) 1
(b) 3
(c) 2
(d) 4
 View Answer
View Answer 
Ans: (b)
d = 7, R = 5, and r = 2
d = R + r
Circles are touching externally. Number of common tangents is 3
Q8: The chords DE and FG of a circle are produced to meet at H. If HE = 6 cm, ED = 9 cm, and HG = 5 cm, then find the length of GF (in cm).
(a) 9
(b) 11
(c) 13
(d) 15
 View Answer
View Answer 
Ans: (c)
We have HE × HD = HG × HF
⇒ 6 × (HE + ED) = 5 × HF
⇒ 6 × (6 + 9) = 5 × HF
⇒ HF = 18 cm
∴ GF = HF - HG = 18 - 5 = 13 cm
Q9: Find the angle subtended by a chord, which makes 120° at the centre, in the minor segment.
(a) 140º
(b) 135º
(c) 120º
(d) 110º
 View Answer
View Answer 
Ans: (c)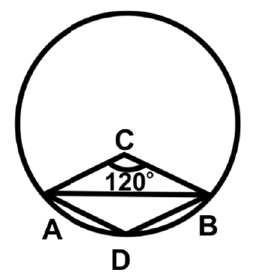
∠ ADB = 1/2 × (Reflex ∠ACB)
1/2 × 240° = 120°
Q10: In the given figure, ‘C’ is the centre of the circle and ∠PQR = 55°. Find reflex ∠PCR.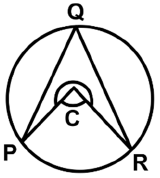 (a) 250º
(a) 250º
(b) 230º
(c) 200º
(d) 290º
 View Answer
View Answer 
Ans: (a)
Given, ∠PQR = 55°.
An angle subtended by an arc at the centre of the circle is double the angle subtended by the same arc at any point on the remaining part of the circle.
∠PCR = 2(∠PQR) =110°
Reflex ∠PCR = 360° - 110° = 250°
Q11: A word and number arrangement machine, when provided with a line of words and numbers, rearranges them according to a specific rule in each step. Below is an example of the input and the steps of rearrangement.
Input: 48 class shine 26 bell 56 edit
Step I: 26 48 class shine bell 56 edit
Step II: 26 48 56 class shine bell edit
Step III: 26 48 56 bell class shine edit
Step IV: 26 48 56 bell class edit shine
Step IV is the final step of the given arrangement. Based on the rule applied in the above steps, what will be the last step for the following input?
Input: 61 place time 32 cat 76 july
(a) Step IV
(b) Step VI
(c) Step V
(d) Step III
 View Answer
View Answer 
Ans: (a)
- The machine rearranges the input by first sorting the numbers in ascending order, followed by the words in alphabetical order.
- For the input "61 place time 32 cat 76 july", the first step will sort the numbers: 32, 61, 76.
- Then, it will arrange the words: "cat", "july", "place", "time".
- Following the same pattern as the previous example, the last step will be Step IV, which is the final arrangement of numbers and words.
Q12: The length of the sides of a triangular mat is 5 cm, 12 cm, and 13 cm. What is the cost of sewing it at the rate of 9 cents per cm2?
(a) $2. 00
(b) $2.16
(c) $2.48
(d) $2.70
 View Answer
View Answer 
Ans: (d)
Semi perimeter of triangle s = 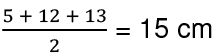
By Heron’s formula: The area of the triangle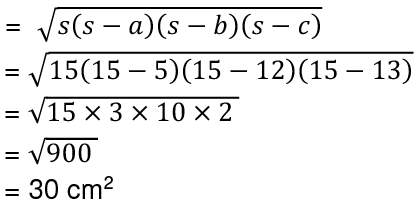 Cost of painting = 30 x 9 = 270 cents = $2.70
Cost of painting = 30 x 9 = 270 cents = $2.70
Q13: Paul tore a piece of cloth which is in the shape of a rhombus of side 100m equally. and gave it to her two brothers. If the line of tearing is 160 m, what area of the cloth did each brother get?
(a) 4840 m2
(b) 4800 m2
(c) 1400 m2
(d). 3600 m2
 View Answer
View Answer 
Ans: (d)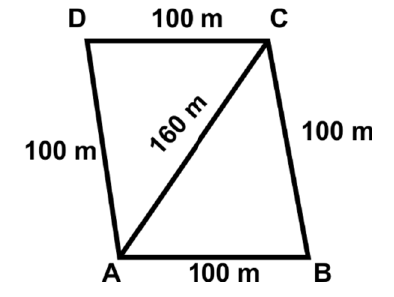
The line of division is along the diagonal of the rhombus-shaped field.
So, each son gets an equal area.
By Heron's formula: Area of triangle is 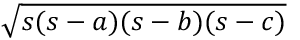
Given: a = 100 m, b = 100 m, and c =160 m
Area of ΔMBC = 
Q14: In a ∆PQR, G is the centroid. What is the ratio of the area of ∆PGR to the area of ∆PQR?
(a) 1 : 2
(b) 1 : 3
(c) 1 : 4
(d) 1 : 6
 View Answer
View Answer 
Ans: (b)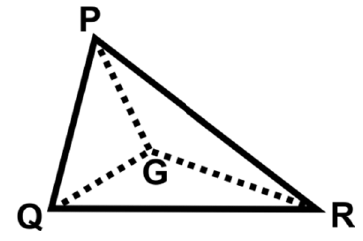 area of ∆PGQ = area of ∆QGR = area of ∆PGR
area of ∆PGQ = area of ∆QGR = area of ∆PGR
Q15: As shown in the figure, the area of the parallelogram LMQO is 48 cm2 and LM // ON. Find the areas of ΔLQM, ΔLPM and ΔLNM.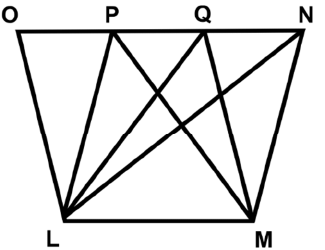 (a) 8 cm2
(a) 8 cm2
(b) 12 cm2
(c) 10 cm2
(d) 24 cm2
 View Answer
View Answer 
Ans: (d)
Given LM // NO and the area of the parallelogram, LMQO is 48cm2
ΔLQM, ΔLPM and ΔLNM and parallelogram LMQO are on the same base and between the same parallels
Area of ΔLQM = Area of ΔLPM = Area of ΔLNM
= 1/2 × Area of parallelogram LMQO
= 1/2 × 48 = 24 cm2
Mathematical Reasoning
Q16: If the diagonals of a quadrilateral intersect each other at right angles, what type of quadrilateral is it?
(a) Parallelogram
(b) Rectangle
(c) Rhombus
(d) Square
 View Answer
View Answer 
Ans: (c)
- When the diagonals of a quadrilateral bisect each other at right angles, it indicates a special property.
- This property is characteristic of a rhombus, which has diagonals that not only bisect each other but also intersect at 90 degrees.
- While a parallelogram has bisecting diagonals, they do not necessarily meet at right angles.
- A rectangle has equal angles but does not guarantee that the diagonals intersect at right angles.
Q17: Determine the value of k that makes x = –1 and y = –1 a solution of the linear equation 9kx + 12ky = 63.
(a) 6
(b) –3
(c) 2
(d) –7
 View Answer
View Answer 
Ans: (b)
- To find the value of k, substitute x = –1 and y = –1 into the equation: 9k(-1) + 12k(-1) = 63.
- This simplifies to -9k - 12k = 63, which combines to -21k = 63.
- Now, divide both sides by -21 to isolate k: k = 63 / -21.
- This results in k = -3, which is the correct answer.
Q18: If x - (1/x) = √7, what is the value of x2 + (1/x2)?
(a) 7
(b) -7
(c) 9
(d) -9
 View Answer
View Answer 
Ans: (c)
- To solve for x2 + (1/x2), we start with the equation x - (1/x) = √7.
- We can square both sides: (x - (1/x))2 = (√7)2, which gives us x2 - 2 + (1/x2) = 7.
- This simplifies to x2 + (1/x2) = 7 + 2 = 9.
- Thus, the value of x2 + (1/x2) is 9.
Q19: If 3 + 2√5 / 3 - 5√5 = (p + q√5), what is the value of 11(p + q)?
(a) 31
(b) –41
(c) –31
(d) –40
 View Answer
View Answer 
Ans: (b)
- To solve the equation, we first simplify the expression 3 + 2√5 / 3 - 5√5.
- By multiplying the numerator and denominator by the conjugate of the denominator, we can eliminate the square root in the denominator.
- This results in a form where we can identify p and q, which are the coefficients of the rational and irrational parts respectively.
- After finding p and q, we calculate 11(p + q) and find that it equals –41.
Q20: The pillars of a temple are cylindrical in shape. If each pillar has a circular base of radius 20 cm and height 10 m, then how much concrete mixture would be required to build 14 such pillars?
(a) 17 m3
(b) 15.6 m3
(c) 17.6 m3
(d) None of these
 View Answer
View Answer 
Ans: (c)
- To find the volume of one cylindrical pillar, we use the formula: Volume = π × radius2 × height.
- The radius is 20 cm, which is 0.2 m (since 100 cm = 1 m). The height is 10 m.
- Calculating the volume of one pillar: Volume = π × (0.2)2 × 10 = π × 0.04 × 10 = 0.4π m3.
- Now, for 14 pillars, the total volume is 14 × 0.4π m3 ≈ 17.6 m3 (using π ≈ 3.14).
Q21: A quadrilateral cannot be constructed if __________.
(a) Its two diagonals and three sides are given.
(b) Its three sides and two included angles are given.
(c) Its two adjacent sides and two angles are given.
(d) Length of its four sides and a diagonal are given.
 View Answer
View Answer 
Ans: (c)
- To construct a quadrilateral, certain conditions must be met.
- When you have two adjacent sides and two angles, it is not enough to determine a unique quadrilateral.
- This is because the angles can lead to different shapes, making it impossible to construct a single quadrilateral.
- In contrast, the other options provide sufficient information to create a quadrilateral.
Q22: What is the length of the longest stick that can be put in a box of dimensions 12 m x 8 m x 9 m?
(a) 17 m
(b) 15 m
(c) 12 m
(d) 18 m
 View Answer
View Answer 
Ans: (a)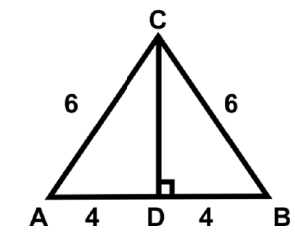 Dimensions of a room = 12 m × 8 m × 9 m
Dimensions of a room = 12 m × 8 m × 9 m
Length of the diagonal = 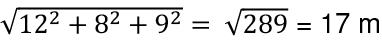
Q23: For which value of p is the polynomial (2x4 + 3x3 + 2px2 + 3x + 6) divisible by x + 2?
(a) 1
(b) 2
(c) 3
(d) –1
 View Answer
View Answer 
Ans: (d)
- To determine the value of p for which the polynomial is divisible by x + 2, we can use the Remainder Theorem.
- According to this theorem, if a polynomial f(x) is divisible by (x - a), then f(a) = 0.
- Here, we substitute x = -2 into the polynomial: f(-2) = 2(-2)4 + 3(-2)3 + 2p(-2)2 + 3(-2) + 6.
- Calculating this gives us: 32 - 24 + 8p - 6 + 6 = 0, which simplifies to 8p + 8 = 0.
- Solving for p, we find p = -1, confirming that the correct answer is (d).
Q24: Which of the following numbers cannot be divided evenly by 11?
(a) 135795
(b) 841763
(c) 359194
(d) 600952
 View Answer
View Answer 
Ans: (b)
- The rule for divisibility by 11 states that you subtract the sum of the digits in odd positions from the sum of the digits in even positions.
- For 841763, the sums are: odd positions (8 + 1 + 6) = 15 and even positions (4 + 7 + 3) = 14. The difference is 1, which is not divisible by 11.
- In contrast, the other numbers can be divided evenly by 11 based on this rule.
- Thus, 841763 is the only number that does not meet the divisibility condition.
Q25: The radius of a cylinder is 7 cm, and its height is 1 cm more than twice its radius. Find the curved surface area of the cylinder.
(a) 680 cm2
(b) 620 cm2
(c) 640 cm2
(d) 660 cm2
 View Answer
View Answer 
Ans: (d)
Curved surface area of a cylinder = 2πrh
h = 7 × 2 + 1 = 15 cm
r = 7 cm
Curved surface area of a cylinder = 660 cm2
Q26: If a = 15/18 and b = 28/36, what is the value of a + b / a - b?
(a) 5/27
(b) 29
(c) 41
(d) 17/72
 View Answer
View Answer 
Ans: (b)
- First, simplify the fractions: a = 15/18 simplifies to 5/6 and b = 28/36 simplifies to 7/9.
- Next, calculate a + b: 5/6 + 7/9. To add these, find a common denominator, which is 18. This gives us (15/18 + 14/18) = 29/18.
- Now, calculate a - b: 5/6 - 7/9. Using the same common denominator, we get (15/18 - 14/18) = 1/18.
- Finally, divide the results: (29/18) / (1/18) = 29, since dividing by a fraction is the same as multiplying by its reciprocal.
Q27: If the coordinates of two points P and Q are (–3, 4) and (–4, 5) respectively, what is the result of the abscissa of P minus the abscissa of Q?
(a) –5
(b) 1
(c) –1
(d) –2
 View Answer
View Answer 
Ans: (b)
- To find the abscissa of point P, we look at its coordinates, which are (–3, 4). The abscissa is the first number, so for P, it is –3.
- For point Q, with coordinates (–4, 5), the abscissa is –4.
- Now, we calculate the difference: abscissa of P (–3) minus abscissa of Q (–4).
- This gives us: –3 - (–4) = –3 + 4 = 1.
Q28: If a pie chart shows the distribution of individuals from various cities out of a total of 2500, and the central angle for the segment representing Patna city is 72°, what is the number of individuals from Patna city?
(a) 500
(b) 720
(c) 550
(d) 700
 View Answer
View Answer 
Ans: (a)
- To find the number of persons from Patna city, we use the formula: (Central Angle / 360) * Total Persons.
- Here, the central angle is 72° and the total number of persons is 2500.
- Calculating: (72 / 360) * 2500 = (1/5) * 2500 = 500.
- Thus, the number of persons from Patna city is 500.
Q29: The perimeter of a triangle is 64 cm. Find the area of the triangle, if two of its sides are 16 cm and 22 cm.
(a) 16√15 cm2
(b) 32√30 cm2
(c) 16√30 cm2
(d) 32√15 cm2
 View Answer
View Answer 
Ans: (b)
- To find the area of the triangle, we first need to determine the length of the third side. Since the perimeter is 64 cm, the third side is 64 - (16 + 22) = 26 cm.
- Next, we can use Heron's formula to calculate the area. First, we find the semi-perimeter, which is (16 + 22 + 26) / 2 = 32 cm.
- Now, applying Heron's formula: Area = √[s(s-a)(s-b)(s-c)], where s is the semi-perimeter and a, b, c are the sides of the triangle.
- Substituting the values: Area = √[32(32-16)(32-22)(32-26)] = √[32 * 16 * 10 * 6] = 32√30 cm2.
Q30: A tablet of medicine is in the shape of a sphere with a diameter of 3.5 mm. What is the volume of medicine (in mm³) required to fill the tablet?
(a) 25.54
(b) 19.21
(c) 22.46
(d) 20.42
 View Answer
View Answer 
Ans: (c)
- To find the volume of a sphere, we use the formula: V = (4/3)πr3.
- The radius (r) is half of the diameter, so r = 3.5 mm / 2 = 1.75 mm.
- Now, substituting the radius into the formula: V = (4/3)π(1.75)3.
- Calculating this gives approximately 22.46 mm3, which is the volume of the tablet.
Q31: Which of the following is not one of Euclid’s axioms?
(a) The whole is greater than the part.
(b) Things which are double of the same things are equal to one another.
(c) Things which are halves of the same things are equal to one another.
(d) If two things are equal, then their sum is equal to 1/3 of the one thing.
 View Answer
View Answer 
Ans: (d)
- Euclid’s axioms are fundamental truths in geometry.
- The statement in option (d) is incorrect because it does not reflect a basic principle of equality.
- In contrast, options (a), (b), and (c) are all valid axioms that describe relationships between parts and wholes.
- Thus, option (d) is the only one that does not belong to Euclid’s axioms.
Q32: If (5/7) - 4X x (7/5) - 7 = (7/5) 9, what is the value of x?
(a) 5
(b) 6
(c) 3
(d) 4
 View Answer
View Answer 
Ans: (d)
- To solve the equation, we first simplify the left side: (5/7) - 4X * (7/5) - 7.
- Next, we can rewrite the equation as (5/7) - 4X * (7/5) = (7/5) 9 + 7.
- After simplifying, we isolate x and find that x equals 4.
- Thus, the correct answer is 4, which is option (d).
Q33: Mahesh sold a chair with an 18% profit. If he had sold it for ₹172 more, he would have made a 22% profit. What is the C.P. of the chair?
(a) ₹4300
(b) ₹2400
(c) ₹3600
(d) ₹2800
 View Answer
View Answer 
Ans: (a)
- Let the C.P. of the chair be x.
- With an 18% profit, the selling price (S.P.) is 1.18x.
- If sold for ₹172 more, the S.P. becomes 1.18x + 172, which gives a 22% profit, so it equals 1.22x.
- Setting the two expressions for S.P. equal: 1.18x + 172 = 1.22x.
- Solving this gives x = ₹4300, which is the C.P. of the chair.
Q34: What will be the curved surface area of a hemisphere whose total surface area is 630 cm2?
(a) 210 cm2
(b) 500 cm2
(c) 450 cm2
(d) 420 cm2
 View Answer
View Answer 
Ans: (d)
We know that:
Curved surface area = 2πr2 sq. units
Total surface area = 3πr2 sq. units
Curved surface area =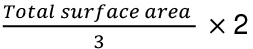
Curved surface area = 420 cm2
Q35: If 10 cubic metres of clay is uniformly spread on a land of area 100 acres, what is the rise in the level of the ground?
(a) 0.001 m
(b) 0.01 m
(c) 0.11 m
(d) 0.1 m
 View Answer
View Answer 
Ans: (a)
Volume of clay = 10m3
Area of land = 100 acres
= 100 × 100 m2 = 10000 m2
Rise in the level of ground = 10/10000 = 0.001 m
Everyday Mathematics
Q36: A small village, with a population of 5000, requires 75 litres of water per head per day. The village has got an overhead tank of measurement 40 m × 25 m × 15 m. For how many days will the water of this tank last?
(a) 30
(b) 32
(c) 40
(d) 45
 View Answer
View Answer 
Ans: (c)
- First, calculate the total volume of the tank: 40 m × 25 m × 15 m = 15,000 m³.
- Convert the volume to litres: 15,000 m³ = 15,000,000 litres (since 1 m³ = 1,000 litres).
- Next, find the daily water requirement for the village: 5000 people × 75 litres = 375,000 litres per day.
- Finally, divide the total water in the tank by the daily requirement: 15,000,000 litres ÷ 375,000 litres/day = 40 days.
Q37: The yearly earnings of Mr. Raj amount to ₹ 500000. If his salary grows at a rate of 20% each year, what will his salary be after 3 years?
(a) ₹ 785000
(b) ₹ 972500
(c) ₹ 765000
(d) ₹ 864000
 View Answer
View Answer 
Ans: (d)
- To find Mr. Raj's salary after 3 years with a 20% annual increase, we can use the formula for compound interest: Final Amount = Principal × (1 + Rate)Time.
- Here, the Principal is ₹ 500000, the Rate is 20% (or 0.20), and the Time is 3 years.
- Calculating it: Final Amount = 500000 × (1 + 0.20)3 = 500000 × (1.20)3 = 500000 × 1.728 = ₹ 864000.
- Thus, after 3 years, Mr. Raj's salary will be ₹ 864000.
Q38: In a park, there is a slide with a triangular side wall that has been painted. The lengths of the sides of the wall are 18 m, 12 m, and 10 m. What is the area that has been painted?
(a) 40√2 m2
(b) 25√3 m2
(c) 15√2 m2
(d) 30√3 m2
 View Answer
View Answer 
Ans: (a)
- To find the area of the triangular wall, we can use Heron's formula. First, we calculate the semi-perimeter (s) of the triangle: s = (18 + 12 + 10) / 2 = 20 m.
- Next, we apply Heron's formula: Area = √[s(s-a)(s-b)(s-c)], where a, b, and c are the sides of the triangle.
- Substituting the values: Area = √[20(20-18)(20-12)(20-10)] = √[20 * 2 * 8 * 10] = √[3200] = 40√2 m2.
- Thus, the area that has been painted is 40√2 m2.
Q39: Manish is 7 years younger than his brother Sumit. After 6 years, Manish’s age will be 7 years more than half the age of Sumit. What is Sumit's current age?
(a) 18 years
(b) 27 years
(c) 22 years
(d) 15 years
 View Answer
View Answer 
Ans: (c)
- Let Sumit's current age be represented as S.
- Then, Manish's current age is S - 7.
- In 6 years, Manish will be (S - 7 + 6) = S - 1 years old.
- At that time, Sumit will be (S + 6) years old.
- The equation states that Manish's age will be 7 years more than half of Sumit's age: S - 1 = 0.5(S + 6) + 7.
- Solving this gives S = 22, which means Sumit's present age is 22 years.
Q40: A can finish a task in 15 days, while B can complete it in 12 days. If B works alone for 8 days and then stops, how many days will A need to finish the leftover work?
(a) 9 days
(b) 7 days
(c) 6 days
(d) 5 days
 View Answer
View Answer 
Ans: (d)
- First, calculate how much work B does in 8 days. B completes 1/12 of the work in a day, so in 8 days, B finishes 8/12 or 2/3 of the work.
- This means 1/3 of the work is still left. A can complete 1/15 of the work in a day.
- To find out how many days A needs to finish the remaining 1/3 of the work, divide 1/3 by 1/15, which equals 5 days.
- Thus, A will take 5 days to complete the remaining work.
Q41: Points A and B are 90 km apart on a highway. A car departs from A at a speed of *x* km/h, while another car leaves from B at a speed of *y* km/h simultaneously. If both cars travel in the same direction, they meet after 9 hours. What is the linear equation that represents this scenario?
(a) x + y = 20
(b) 2x + y = 9
(c) 3x + 4y = 20
(d) None of these
 View Answer
View Answer 
Ans: (d)
- The distance between A and B is 90 km.
- Both cars travel for 9 hours before meeting.
- If they are moving in the same direction, the distance covered by the car from A plus the distance covered by the car from B must equal 90 km.
- The equation can be set up as: 9x - 9y = 90, which simplifies to x - y = 10. This does not match any of the provided options, hence the answer is None of these.
Q42: A P.T. teacher aims to organize the largest possible group of 6000 students in a field, ensuring that the number of rows matches the number of columns. Determine the number of rows if 71 students remain unarranged.
(a) 70
(b) 77
(c) 60
(d) None of these
 View Answer
View Answer 
Ans: (b)
- To find the number of rows, we first calculate how many students can be arranged in a square formation. This means we need to find the largest perfect square less than or equal to 6000.
- The largest perfect square less than 6000 is 5929, which is 77 squared (77 x 77 = 5929).
- Since 71 students are left out, we subtract 71 from 6000, giving us 5929, which confirms that 77 rows and 77 columns can be formed.
- Thus, the number of rows is 77, as it matches the number of columns.
Q43: How much water needs to be added to a tank that holds 45 litres of milk priced at ₹4 per litre in order to lower the cost of the milk to ₹3 per litre?
(a) 8 litres
(b) 10 litres
(c) 12 litres
(d) 15 litres
 View Answer
View Answer 
Ans: (d)
- To find out how much water to add, we first calculate the total cost of the milk: 45 litres x ₹4 = ₹180.
- Next, we want the new cost per litre to be ₹3. If we add 'x' litres of water, the total volume becomes (45 + x) litres.
- We set up the equation: ₹180 / (45 + x) = ₹3.
- Solving this gives us x = 15 litres. Therefore, we need to add 15 litres of water to achieve the desired cost.
Q44: Two pipes A and B can fill a cistern in 9 hours and 12 hours respectively. If both the pipes are opened alternately for 1 hour, starting from A, then how much time will the cistern take to be filled?
(a) 10(1/2) hours
(b) 10(1/4) hours
(c) 10(2/3) hours
(d) 10(1/3) hours
 View Answer
View Answer 
Ans: (b)
- Pipe A fills the cistern in 9 hours, so it fills 1/9 of the cistern in 1 hour.
- Pipe B fills the cistern in 12 hours, so it fills 1/12 of the cistern in 1 hour.
- When both pipes are used alternately for 1 hour each, in 2 hours, they fill 1/9 + 1/12 of the cistern.
- Calculating this gives a total of 5/36 of the cistern filled in 2 hours.
- To fill the entire cistern, it will take 10(1/4) hours when both pipes are used alternately.
Q45: In a class of 60 students, 21 students enjoy singing, 17 students enjoy dancing, and the remaining students participate in other activities. If a student is chosen at random, what is the probability that the student will prefer other activities?
(a) 14/30
(b) 19/30
(c) 17/30
(d) 11/30
 View Answer
View Answer 
Ans: (d)
- First, calculate the total number of students who like singing and dancing: 21 + 17 = 38.
- Next, find the number of students who like other activities: 60 - 38 = 22.
- The probability of selecting a student who likes other activities is the number of students who like other activities divided by the total number of students: 22/60.
- Simplifying 22/60 gives us 11/30, which is the correct answer.
Achievers Section
Q46: Answer the following questions and choose the correct option.
(i) Given that p + q + r = 6 and pq + qr + rp = 5, determine the value of p3 + q3 + r3 - 3pqr.
(ii) If x + y = 5 and xy = 6, calculate the value of x3 + y3.
(a) 284
(b) 126
(c) 252
(d) 100
 View Answer
View Answer 
Ans: (b)
- To solve for p3 + q3 + r3 - 3pqr, we can use the identity: p3 + q3 + r3 - 3pqr = (p + q + r)((p + q + r)2 - 3(pq + qr + rp)).
- Substituting the values: p + q + r = 6 and pq + qr + rp = 5, we get: 6(6² - 3*5) = 6(36 - 15) = 6*21 = 126.
- Thus, the value of p3 + q3 + r3 - 3pqr is 126.
- Therefore, the correct answer is option (b) 126.
Q47: Rachel conducted an experiment in which she collected all the containers in the lab of the same size (cone-shaped). She found that the inner measures of the containers are of radius 3 cm and height 7 cm. If the number of containers in the lab is 100, then calculate approximately, how much will be the volume of all the containers.
(a) 6000 cm3
(b) 6600 cm3
(c) 6400 cm3
(d) 13200 cm3
 View Answer
View Answer 
Ans: (b)
Volume all the containers = Volume of one container × Number of containers
Volume all the containers = 1/3 πr2h × 100
Volume all the containers = 6600 cm3
Q48: The two adjacent sides of a rectangle PQRS are the halves of the diagonals of the rhombus PMNR, respectively. If PQ = 4 cm and QR = 3 cm, then find the ratio of the perimeter of the rectangle and the rhombus.
(a) 14 : 13
(b) 13 : 20
(c) 7 : 10
(d) 7 : 11
 View Answer
View Answer 
Ans: (c)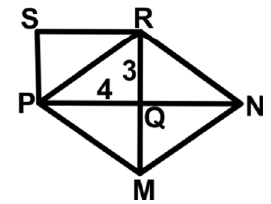 From the figure, PR = 5 cm [Pythagoras theorem]
From the figure, PR = 5 cm [Pythagoras theorem]
Perimeter of the rectangle = 7 + 7 = 14 cm
Perimeter of the rhombus = 4 × 5 = 20 cm
Ratio of their perimeters = 14 : 20
= 7 : 10
Q49: Ren is given two coordinates namely A (5, -2) and B (3, 2). She is informed that A is the vertex of a square and B is the midpoint of one of the diagonals. The area of the square is:
(a) 40
(b) 20
(c) 60
(d) 70
 View Answer
View Answer 
Ans: (a)
Let the endpoint of the diagonal be (x, y)
x = 1 and y = 6
Length of diagonal = 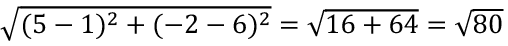
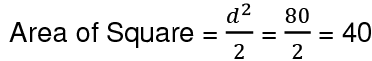
Q50: As shown in the figure, Given L (4, 6) and M (0, 3) respectively. Find the area of quadrilateral LMOP (in sq. units).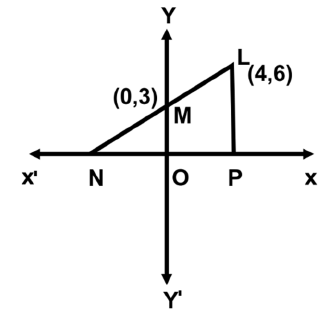
(a) 20
(b) 16
(c) 18
(d) 24
 View Answer
View Answer 
Ans: (c)
Let ON = x units
In ΔMNO ~ ΔLNP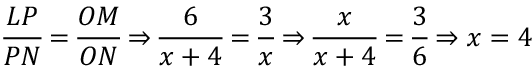
N is (-4,0)
Area of trapezium. LMOP = 1/2 (OM + LP) · OP = 1/2 (3 + 6) · 4 = 18 sq units
|
25 videos|117 docs|45 tests
|
FAQs on Maths Olympiad Previous Year Paper -2 - Mathematics Olympiad for Class 9
| 1. What topics are covered in the Class 9 Maths Olympiad exam? |  |
| 2. How can I prepare effectively for the Class 9 Maths Olympiad? |  |
| 3. What is the format of the Class 9 Maths Olympiad exam? |  |
| 4. Where can I find previous year papers for Class 9 Maths Olympiad? |  |
| 5. What are the benefits of participating in the Maths Olympiad for Class 9 students? |  |















