Mathematics Exam > Mathematics Notes > Mathematics for Competitive Exams > Matrices and Determinants- 2
Matrices and Determinants- 2 | Mathematics for Competitive Exams PDF Download
| Table of contents |

|
| Properties on Matrices |

|
| Properties on Determinants |

|
| Properties on Inverse of a Matrix |

|
| Rank of a Matrix |

|
| Properties on Trace |

|
Properties on Matrices
- A + B = B + A [Commutative]
- (A + B) + C = A + (B + C) [Associativity]
- A + O = A = O + A [Existence of Identity]
- -A + A = O = A + (-A) [Existence of Inverse]
- A + B = A + C ⇒ B = C ⇒ B + A = C + A ⇒ B = C [Cancellation law]
- The equation A + X = O has a unique solution in the set of all A (m × n) matrices
- k(A + B) = kA + kB [k be any scalar]
- (p + q)A = pA + qA [p, q are two scalars]
- (pq)A = p(qA)
- (-K)A = -(KA) = K(-A)
- 1A = A, (-1)A = -A
- -(A + B) = -A - B
- If the product AB exists, then it is not necessary that BA Product also exist.
- A(BC) = (AB)C [Associativity]
- A(B + C) = AB + AC [distributive]
- The equation AB = 0 does not necessarily imply that at least one of matrices A and B must be a zero matrix.
- If AB = 0, then it does not necessarily imply that BA = 0
- AII = A = InA
- A2 - B2 = (A - B)(A + B) is true only if matrices A and B commute
- The product of two triangular matrices is itself triangular.
- If a diagonal matrix is commutative with every matrix of the same order then it is necessary a scalar matrix.
- If AB = A and BA = B then A and B are idempotent
- If B is an idempotent matrix, then A = I - B is also idempotent and that AB = BA = 0
- A is involuntary iff (I + A)(I - A) = 0
- tr(kA) = k.tr(A)
- tr(A + B) = tr(A) + tr(B)
- tr(AB) = tr(BA)
- (AT)T = A
- (A + B)T = AT + BT
- (AB)T = BT AT
- Let
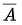 denote the Complex conjugate of A then
denote the Complex conjugate of A then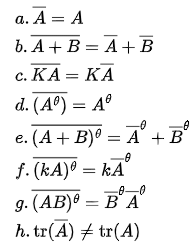
- A is a skew-symmetric then is diagonal elements are all zero
- The diagonal elements of a skew-symmetric matrix all are zero
- Every diagonal element of Hermitian matrix must be real
- The diagonal elements of skew-Hermitian matrix must be purely imaginary numbers or zero
- For any non-zero real k if A is symmetric (skew-symmetric) then kA is also symmetric (skew-symmetric)
- If A is Hermitian Matrix then iA is skew Hermitian
- If A is a skew-Hermitian matrix, iA is Hermitian
- (AB)T = BTAT
- For real matrices A, B and C
a. ATA = 0 iff A = 0
b. AB = 0 iff ATAB = 0
c. AB = AC iff ATAB = ATAC - (AB)T = ATBT iff AB = BA
- If A and B be diagonal matrices then AB is also diagonal and that AB = BA
- Let A be square real matrix then
a. A + AT is symmetric, even if A is not symmetric
b. AB is not necessarily symmetric if A and B are
c. ATBA is symmetric if B is symmetric but that the converse need not be true - Let A be a square real matrix
a. A - AT is skew-symmetric
b. A can be decomposed into the sum of a symmetric and a skew-symmetric matrix
Properties on Determinants
- The sum of the products of the elements of any row or column with the corresponding cofactors of the matrix is equal to the value of the determinant.
- The sum of the products of the elements of any row and the cofactors of some other row is zero.
- Let ( A = (aij) be square matrix of order n , and let Cij be the cofactor of aij then
- The determinant of a triangular matrix is the product of its diagonal elements
- For any two square matrices of the same order, |AB| = |A||B|
- The value of the determinant of a diagonal matrix is equal to the product of the elements lying along its principal diagonal
- The value of the determinant of a unit matrix is always equal to 1
- The value of the determinant of a triangular matrix (Upper or lower) is equal to the product of the elements lying along its principal diagonal
- The value of a determinant does not change when rows and columns are interchanged. |A| = |AT|
- If any two rows (or two columns) of a determinant are interchanged, the value of the determinant is multiplied by -1
- If all the elements of one row (or one column) of a determinant are multiplied by the same number k, the value of the row determinant is k times the value of the determinant.
- If A be an n-rowed square matrix, and k be any scalar, then |kA| = kn|A|
- If two rows (or two columns) of a determinant are identical, the value of the determinant is zero
- The value of the determinant of a skew-symmetric odd order is always zero
- If in a determinant each element in any row or column consists of the sum of two terms, then the determinant can be expressed as the sum of two determinants of the same order
- If to the element of a row (or column) of a determinant is added M times the corresponding elements of another row (or column), the value of the determinant thus obtained is equal to the value of the original determinant
- Let A be a square matrix then
a. |AT| = |A|
b. |A| = |A|
c. |Aθ| = |A|
Properties on Inverse of a Matrix
- (Adj A)A = A(Adj A) = |A|In
- Every invertible matrix possess a unique inverse
- (AB)-1 = B-1A-1
- (AT)-1 = (A-1)T
- (A-1)θ = (Aθ)-1
- adj . 0 = 0
- adj . In = In
- adj AT = (adj A)T
- If A is a symmetric matrix, then adj A is also symmetric
- If A is symmetric then A-1 is also symmetric
- The adjoint of a diagonal matrix of order 3 is a diagonal matrix
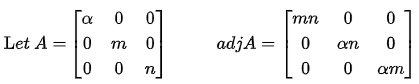
det(A-1) = (det A)-1
- If B is non-singular, then matrices A and B-1AB have the same det A & B of A
- If matrices A and B commute, then A-1 and B-1 also commute
- If A, B, C are three matrices conformable for multiplication then (ABC)-1 = C-1B-1A-1
- If a matrix A is non-singular, then AB = AC ⇒ B = C, where B and C are square matrices of the same order as A
- If the product of two non-zero square matrices is a zero matrix, then both of them must be singular.
- If |A| = 0, then |adj A| = 0
- adj(AB) = adj B · adj A
- If A · B be n-rowed orthogonal matrices AB and BA are also orthogonal matrices
- If A, B be n-rowed unitary matrices, AB and BA are also unitary
Rank of a Matrix
- The rank of a matrix A is r if it possess the following two properties
a. There is at least one square sub matrix of A of order r whose determinant is not equal to zero
b. And all the matrix A Counting any square sub matrix of order r+1, then the determinant of every square sub matrix of A of order r+1 should be zero. - The rank of matrix is the order of any highest order non-vanishing minor of the matrix.
- The rank of every non-singular matrix of order n is n.
- The rank of a square matrix A of order n less than n iff A is singular i.e. |A| = 0
- The rank of every non-zero matrix is ≥ 1
- The rank of a matrix is ≤ r, if all (r+1)-rowed minors of the matrix vanish
- The rank of a matrix is ≥ r, if there exists r-rowed minor of the matrix which is not equal to zero
- The rank of a matrix in Echelon form is equal to the number of non-zero rows of the matrix.
- The rank of the transpose of a matrix is same as that of original matrix.
- The rank of matrix every element of which is unity is 1
- A is a non-zero column and B a non-zero row matrix then rank(AB) = 1
- Rank of a matrix is ≥ the rank of every sub matrix
- Rank of skew-symmetric matrix cannot be rank 1
- Let A be an m x n matrix.
a. 0 ≤ rank(A) ≤ min{m,n}
b. rank(A) = 0 ⇔ A = 0
c. rank(Iₙ) = n
d. rank(kA) = k.rank(A) if k ≠ 0 - Let A be an m x n matrix and let Ax = 0 for some x ≠ 0 ⇔ rank(A) ≤ n - 1
- The rank of diagonal matrix equals the number of non-zero diagonal elements it possess but is not true for triangular matrix.
- Every m x n matrix A of rank r can be written as A = B Cᵀ, where B(m x r) and C(m x r) both have rank r
rank(A + B) ≤ rank(A) + rank(B). - rank(A + B) ≤ rank(A) + rank(B)
- rank(A - B) ≥ |rank(A) - rank(B)|
- rank(AB) ≤ min(rank(A), rank(B))
- rank(AB) ≠ rank(BA)
- Let A₁ be a sub matrix of A then rank(A₁) ≤ rank(A)
- rank(AᵀAB) = rank(AB) = rank(ABBᵀ) for any conformable matrices A and B.
- rank(A) = rank(Aᵀ) = rank(AAᵀ) = rank(AᵀA)
- Let A be an m × n matrix, and let B(m × n) and C(m × n) be non-singular
a. rank(BA) = rank(A)
b. rank(AC) = rank(A)
c. rank(BAC) = rank(A) - For conformable matrices A, B, C
a. rank(BA) = rank(BᵀBA)
b. rank(AC) = rank(ACCᵀ)
c. rank(BA) = rank(A)
d. rank(AC) = rank(A)
Properties on Trace
- Let A and B be square matrices of the same order, and let k and m be positive scalars, then
a. tr(A + B) = tr(A) + tr(B)
b. tr(kA) = ktr(A)
c. tr(kA + mB) = ktr(A) + mtr(B)
d. tr(AT) = tr(A)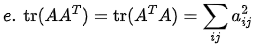
- For any real matrix A, tr(ATA) ≥ 0, with tr(ATA) = 0 iff A = 0
- Let A and B be m x n matrices, then tr(ATB) = tr(BAT) = tr(ABT) = tr(BTA)
- tr(ABC) = tr(CAB) = tr(BCA) but tr(ABC) = tr(ACB) is not true
- A real square matrix A is normal if ATA = AAT
a. Every symmetric matrix is normal.
b. Every orthogonal matrix is normal
c. Let A be a normal 2 x 2 matrix then A is either symmetric or has the form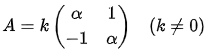
- AP is symmetric when A is symmetric.
- Consider an n×n triangular matrix A. Then all the positive integral power of A are also triangular.
- For two real matrices A and B of the same order then Inner product is defined as ⟨A,B⟩=∑i,j aijbij=tr ATB
a. ⟨A,B⟩=⟨B,A⟩
b. ⟨A,B+C⟩=⟨A,B⟩+⟨A,C⟩
c. ⟨kA,B⟩=k⟨A,B⟩
d. ⟨A,A⟩≥0 with ⟨A,A⟩=0⇔A=0 - For a real matrix A, the Norm of a matrix is defined as
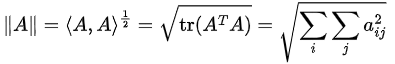 a. ‖kA‖=|k|.‖A‖b. ‖A‖≥0, with ‖A‖=0 iff A=0
a. ‖kA‖=|k|.‖A‖b. ‖A‖≥0, with ‖A‖=0 iff A=0
c. ‖A+B‖≤‖A‖+‖B‖ (triangular inequality) - Let A and B are square matrix of same of order. AB = I if BA = I
- Let A be an orthogonal matrix of order n
a. A is non-singular
b. AT = A-1
c. AT is orthogonal
d. AB is orthogonal when B is orthogonal - If A is orthogonal, |A| = ±1
- If A is non-singular, |A-1| = |A|-1
- Let
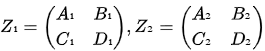 then
then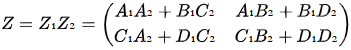
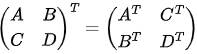
If A and D are square, not necessarily of the same order,
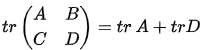
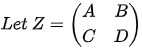 where A and D are square matrices, not necessarily of the same order.
where A and D are square matrices, not necessarily of the same order.
a. If Z is symmetric then A and D are symmetric.
b. If Z is diagonal then A and D are diagonal.
c. If Z is upper triangular then A and D are upper triangular.
d. All the above three statements are necessary but not sufficient.
The document Matrices and Determinants- 2 | Mathematics for Competitive Exams is a part of the Mathematics Course Mathematics for Competitive Exams.
All you need of Mathematics at this link: Mathematics
|
98 videos|34 docs|32 tests
|
FAQs on Matrices and Determinants- 2 - Mathematics for Competitive Exams
| 1. What are the key properties of matrices? |  |
Ans.The key properties of matrices include closure under addition and multiplication, the existence of additive and multiplicative identities, the associative and distributive properties, and the existence of inverses for square matrices. Additionally, the transpose of a matrix has properties like \((A^T)^T = A\) and \((AB)^T = B^T A^T\).
| 2. How do determinants behave under matrix operations? |  |
Ans.Determinants have several important properties: the determinant of a product of matrices is the product of their determinants, \(\text{det}(AB) = \text{det}(A) \cdot \text{det}(B)\); the determinant of a transpose is equal to the determinant of the original matrix, \(\text{det}(A^T) = \text{det}(A)\); and swapping two rows of a matrix multiplies the determinant by \(-1\).
| 3. When is a matrix invertible based on its determinant? |  |
Ans.A matrix is invertible (also known as non-singular) if and only if its determinant is non-zero. If the determinant is zero, the matrix is singular and does not have an inverse.
| 4. What are the properties of the inverse of a matrix? |  |
Ans.Properties of the inverse of a matrix include: \((A^{-1})^{-1} = A\); \((AB)^{-1} = B^{-1}A^{-1}\); and if \(A\) is an invertible matrix, then \(A^T\) is also invertible, and \((A^T)^{-1} = (A^{-1})^T\).
| 5. Can you explain the relationship between the determinant and the inverse of a matrix? |  |
Ans.The relationship is that for an invertible matrix \(A\), the determinant of the inverse is the reciprocal of the determinant of the matrix, expressed as \(\text{det}(A^{-1}) = \frac{1}{\text{det}(A)}\). This means that if the determinant of \(A\) is zero, \(A\) has no inverse.
Related Searches



















