Matrix-Match Type Questions: Vector Algebra and Three Dimensional Geometry - 2 | JEE Advanced | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download
DIRECTIONS (Q. 7-9) : Each question has matching lists. The codes for the lists have choices (a), (b), (c) and (d) out of which ONLY ONE is correct.
Q. 7. Match List I with List II and select the correct answer using the code given below the lists :
List I List II
P. Volume of parallelepiped determined by vectors 1. 100
Then the volume of the parallelepiped determined by vectors
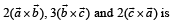
Q. Volume of parallelepiped determined by vectors 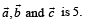 2. 30
2. 30
Then the volume of the parallelepiped determined by vectors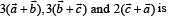
R. Area of a triangle with adjacent sides determined by vectors 3. 24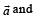
 Then the area of the triangle with adjacent sides
Then the area of the triangle with adjacent sides
determined by vectors 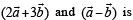
S. Area of a parallelogram with adjacent sides determined by vectors 4. 60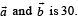 Then the area of the parallelogram with adjacent sides
Then the area of the parallelogram with adjacent sides
determined by vectors 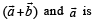

Ans. (c)
Solution. 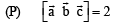
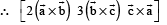
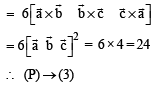
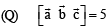
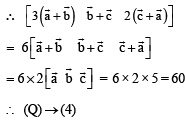
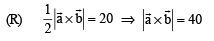
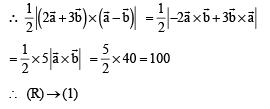
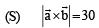
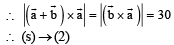
Q. 8. Consider the lines 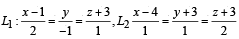 and the planes P1 : 7x + y + 2z = 3, P2 = 3x + 5y – 6z = 4. Let ax + by + cz = d be the equation of the plane passing through the point of intersection of lines L1 and L2, and perpendicular to planes P1 and P2.
and the planes P1 : 7x + y + 2z = 3, P2 = 3x + 5y – 6z = 4. Let ax + by + cz = d be the equation of the plane passing through the point of intersection of lines L1 and L2, and perpendicular to planes P1 and P2.
Match List I with List II and select the correct answer using the code given below the lists :

Ans. (a)
Solution. Any point on L1 is (2λ + 1, – λ, λ – 3) and that on L2 is (μ + 4, μ – 3, 2μ –3)
For point of intersection of L1 and L2 2λ + 1 = μ + 4, – λ = μ – 3, λ – 3 = 2μ – 3 ⇒ λ = 2, μ = 1
∴ Intersection point of L1 and L2 is (5, –2, – 1)
∵ ax + by + cz = d is perpendicular to p1 & p2
∴ 7a + b + 2c = 0 and 3a + 5b – 6c = 0
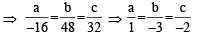
∴ Equation of plane is x – 3y – 2z = d
As it passes through (5, –2, –1)
∴ 5 + 6 + 2 = d = 13
∴ a = 1, b = –3, c = –2, d = 13
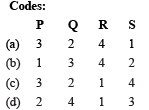
or (P) → (3) (Q) → (2) (R) → (4) (S) → (1)
Q. 9. Match List I with List II and select the correct answer using the code given below the lists :
List - I List - II
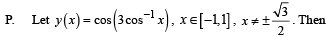 1. 1
1. 1
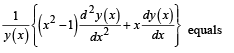
Q. Let A1, A2, ..., An (n > 2) be the vertices of a regular 2. 2
polygon of n sides with its centre at the origin. Let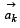
be the position vector of the point Ak, k = 1, 2, ....., n.
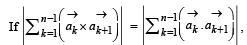
then the minimum value of n is
R. If the normal from the point P(h, 1) on the ellipse 3. 8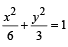 is perpendicular to the line x + y = 8, then the
is perpendicular to the line x + y = 8, then the
value of h is
S. Number of positive solutions satisfying the equation 4. 9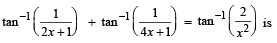

Ans. (a)
Solution.
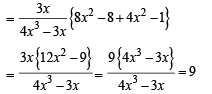
Q(3) ... A1, A2, A3, ... An are the vertices of a regular 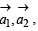
 are their position vectors.
are their position vectors.
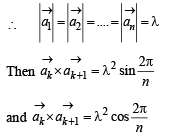
Hence given equation reduces to
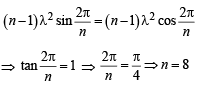
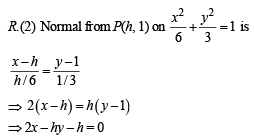
It is perpendicular to x + y = 8
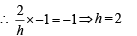
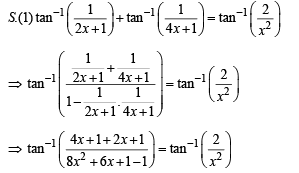
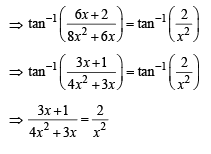
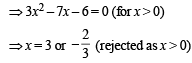
∴ Only one +ve solution is there
Hence (a) is the correct option.
DIRECTIONS (Q. 10-11) : Each question contains statements given in two columns, which have to be matched. The statements in Column-I are labelled A, B, C and D, while the statements in Column-II are labelled p, q, r, s and t. Any given statement in Column-I can have correct matching with ONE OR MORE statement(s) in Column-II. The appropriate bubbles corresponding to the answers to these questions have to be darkened as illustrated in the following example :
If the correct matches are A-p, s and t; B-q and r; C-p and q; and D-s then the correct darkening of bubbles will look like the given.

Q. 10. Match the following :
Column I Column II
(A) In R2, if the magnitude of the projection vector of the vector (p) 1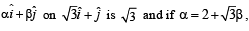 then possible value
then possible value
of |α| is/are
(B) Let a and b be real numbers such that the function (q) 2
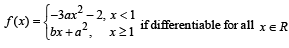
Then possible value of a is (are)
(C) Let ω ≠ 1 be a complex cube root of unity. (r) 3
If 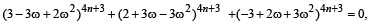
then possible value (s) of n is (are)
(D) Let the harmonic mean of two positive real numbers a and b be 4. (s) 4
If q is a positive real number such that a, 5, q, b is an arithmetic
progression, then the value(s) of | q – a | is (are)
Ans. (A) → q; (B) → p, q; (C) → p, q, s, t; (D) → q, t
Solution.
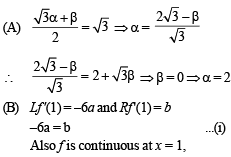
∴–3a – 2 = b + a2
⇒ a2 – 3a + 2 = 0 (using (i))
⇒ a = 1, 2
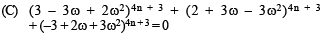
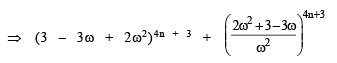
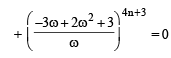
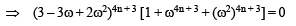
⇒ 4n + 3 should be an integer other than multiple of 3.
∴ n = 1, 2, 4, 5
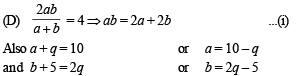
Putting values of a and b in eqn(i)
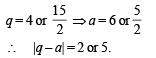
Q. 11. Match the following :
Column I Column II
(A) In a triangle DXYZ, let a, b, and c be the lengths (p) 1
of the sides opposite to the angles X, Y and Z,
respectively. If 2(a2 – b2) = c2 and 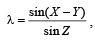
, then possible values of n for which cos(nπλ) = 0 is (are)
(B) In a triangle DXYZ, let a, b and c be the lengths of the (q) 2
sides opposite to the angles X, Y, and Z respectively. If
1 + cos 2X – 2cos 2Y = 2 sin X sin Y, then possible value
(s) of a/b is (are)
(C) In R2, let 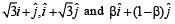 be the position (r) 3
be the position (r) 3
vectors of X , Y and Z with respect to the origin O,
respectively. If the distance of Z from the bisector of the
acute angle of 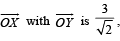 then possible
then possible
value(s) of |β| is (are)
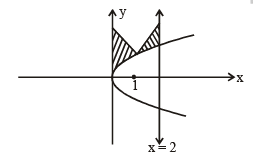
(D) Suppose that F(a) denotes the area of the region bounded (s) 5
by x = 0, x = 2, y2 = 4x and y =| αx- 1 | + | αx- 2 | +αx ,
where a∈ {0, 1} . Then the value(s) of 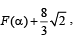 , when
, when
a = 0 and a = 1, is (are)
(t) 6
Ans. (A)→p, r, s; (B) → p; (C) → p, q; (D)→s, t
Solution. (A) 2(a2 – b2) = c2
⇒ 2(sin2x – sin2y) = sin2z
⇒ 2sin(x + y) sin(x – y) = sin2z
⇒ 2sin(x – y) = sin z (∵sin(x + y) = sin z)
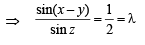
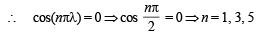
(B) 1 + cos2X – 2cos2Y = 2sinXsinY
⇒ 2cos2X – 2cos2Y = 2sinXsinY
⇒ 1 – sin2X – 1 + 2sin2Y = sinXsinY
⇒ sin2X + sinXsinY – 2sin2Y = 0
⇒ (sinX – sinY) (sinX + 2sinY) = 0
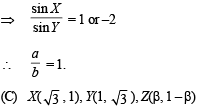
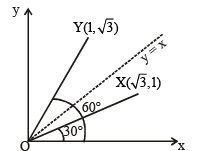
By symmetry, acute angle bisector of ÐXOY is y = x.
∴ Distance of Z from bisector
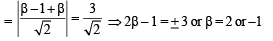
∴ |β| = 1, 2 (D)
For α = 0, y = 3
For α = 1, y = |x – 1| + |x – 2| + x
Case I
F(aα) is the area bounded by x = 0, x = 2, y2 = 4x and y = 3
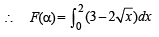
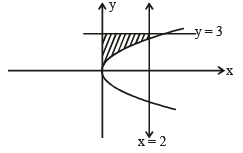

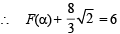
Case II
F(α) is the area bounded by x = 0, x = 2, y2 = 4x and y = |x – 1| + |x – 2| + x
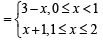
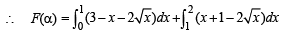
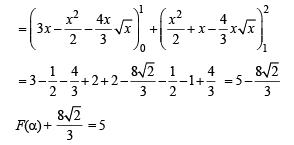
|
347 docs|185 tests
|
|
347 docs|185 tests
|

|
Explore Courses for JEE exam
|

|

















