Matrix-Match Type Questions: Vector Algebra and Three Dimensional Geometry - 1 | JEE Advanced | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download
DIRECTIONS (Q. 1-6) : Each question contains statements given in two columns, which have to be matched. The statements in Column-I are labelled A, B, C and D, while the statements in Column-II are labelled p, q, r, s and t. Any given statement in Column-I can have correct matching with ONE OR MORE statement(s) in Column-II. The appropriate bubbles corresponding to the answers to these questions have to be darkened as illustrated in the following example :
If the correct matches are A-p, s and t; B-q and r; C-p and q; and D-s then the correct darkening of bubbles will look like the given.

Q. 1. Match the following :
(A) Two rays x + y = |a| and ax – y = 1 intersects each other in the (p) 2
first quadrant in the interval a ∈ (a0, ∞), the value of a0 is
(B) Point (α , β , γ) lies on the plane x + y + z = 2. (q) 4/3
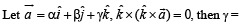
(C) 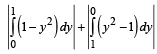 (r)
(r) 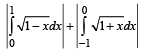
(D) If sinA sinB sinC + cosA cosB = 1, then the value of sinC = (s) 1
Ans. (A) → s; (B) → p; (C) → r, q; (D) → s
Solution. (A) On solving the given equations x + y = |a| and ax – y = 1, we get
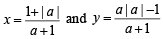
∴ Rays intersect each other in I quad.
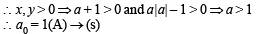
(B) (α, β, γ) lies on the plane x + y + z = 2
⇒ α + β + γ = 2
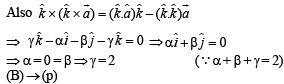
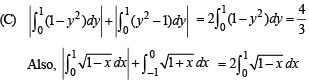
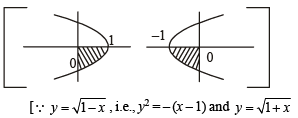
i.e., y2 = (x + 1) represent same area under the given limits]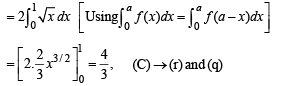
(D) Given : sin A sin B sin C + cos A cos B = 1
But sin A sin B sin C + cos A cos B < sin A sin B + cos
A cos B = cos (A – B)
⇒ cos (A – B) > 1 ⇒ cos (A – B) =1
⇒ A – B = 0 ⇒ A = B
∴ Given relation becomes sin2A sin C + cos2 A = 1
⇒ sin C = 1,
(D) → (s)
Q. 2. Consider the following linear equations ax + by + cz = 0; bx + cy + az = 0; cx + ay + bz = 0
Match the conditions/expressions in Column I with statements in Column II and indicate your answer by darkening the appropriate bubbles in the 4 × 4 matrix given in the ORS.
Column I Column II
(A) a + b + c ≠ 0 and a2 + b2 + c2 = ab + bc + ca (p) the equations represent planes meeting only at asingle point
(B) a + b + c = 0 and a2 + b2 + c2 ≠ ab + bc + ca (q) the equations represent the line x = y = z.
(C) a + b + c ≠ 0 and a2 + b2 + c2 ≠ ab + bc + ca (r) the equations represent identical planes.
(D) a + b + c = 0 and a2 + b2 + c2 = ab + bc + ca (s) the equations represent the whole of the three dimensional space.
Ans. (A) → r; (B) → q; (C) → p; (D) → s
Solution. Here we have, the determinant of the coefficient matrix of given equation, as
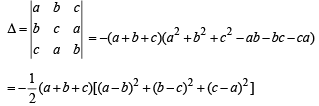
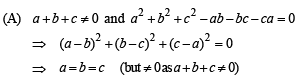
This equation represent identical planes.
(B) a +b +c = 0 and a2 + b2+ c2 - ab - bc - ca ≠ 0
⇒ Δ = 0 and a, b, c are not all equal.
∴ All equations are not identical but have infinite many solutions.
∴ ax + by = (a+ b)z (using a+b+c = 0) and bx + cy = (b+ c)z
⇒ (b2 - ac) y = (b2- ac)z ⇒ y = z
⇒ ax + by + cy= 0 ⇒ ax = ay ⇒ x = y
⇒ x = y = z
∴ The equations represent the line x = y = z
(C) a + b + c ≠ 0 and a2 + b2+ c2 - ab - bc - ca ≠ 0
⇒ Δ ≠ 0 ⇒ Equations have only trivial solution i.e., x = y = z = 0
∴ the equations represents the three planes meeting at a single point namely origin.
(D) a +b +c= 0 and a2 + b2+ c2 - ab - bc - ca = 0
⇒ a = b = c and Δ = 0 ⇒ a = b = c = 0
⇒ All equations are satisfied by all x, y, and z.
⇒ The equations represent the whole of the three dimensional space (all points in 3–D)
Q. 3. Match the statements / expressions given in Column-I with the values given in Column-II.
Column-I Column-II
(A) Root(s) of the equation 2 sin2 θ + sin2 2θ = 2 (p) π/6
(B) Points of discontinuity of the unction 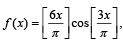 (q) π/4
(q) π/4
f where [y] denotes the largest integer less than or equal to y
(C) Volume of the parallelopiped with its edges represented by (r) π/3
the vectors 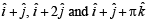
(D) Angle between vector 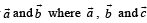 are unit vectors (s) π/2
are unit vectors (s) π/2
satisfying 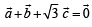
(t) π
Ans. A → q,s; B → p,r,s, t; C → t; D→ r
Solution.
(A) The given equation is
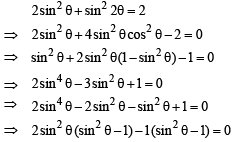
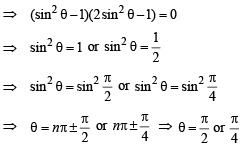
(B) We know that [x] is discontinuous at all integral values, therefore 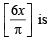 discontinuous at
discontinuous at 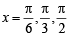 and π. Also cos
and π. Also cos 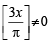 for any of these values of x.
for any of these values of x.
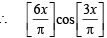 is discontinuous at
is discontinuous at 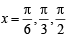 and π.
and π.
(C) We know that th e volume of a par allelopipe with coterminus edges as 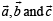 is given by
is given by 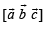
∴ The required volume is 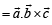
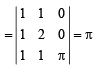
(where θ is the angle between 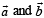 )
)
Q. 4. Match the statements/expressions given in Column-I with the values given in Column-II.
Column-I Column-II
(A) The number of solutions of the equation (p) 1

(B) Value(s) of k for which the planes k x + 4y + z = 0, (q) 2
4x + k y + 2z = 0 and 2x + 2y + z = 0 intersect in a straight line
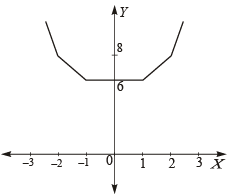
(C) Value(s) of k for which | x – 1 | + | x – 2 | + | x + 1 | (r) 3
| + | x + 2 | = 4k has integer solution(s)
(D) If y' = y + 1 and y (0) = 1, then value(s) of y (1n 2) (s) 4
(t) 5
Ans. A → p;B → q, s;C → q, r, s, t;D→ r
Solution. (A) For the solution of 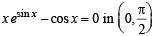
Let us consider two functions
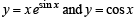
The range of 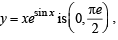 also it is an increasing function on
also it is an increasing function on  Their graph are as shown in the figure below :
Their graph are as shown in the figure below :
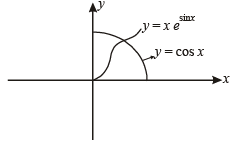
Clearly the two curves meet only at one point, therefore the given equation has only one solution in 
(B) Three given planes are
kx + 4 y +z = 0
4x + ky + 2z = 0
2x + 2 y +z = 0
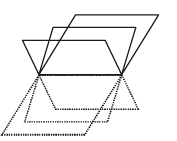
Clearly all the planes pass through (0,0,0).
∴ Their line of intersection also pass through (0, 0, 0) Let a, b, c, be the direction ratios of required line, then we should have
ka + 4b +c = 0
4a + kb + 2c = 0
2a + 2b +c = 0
For the required line to exist the above system of equations in a, b, c, should have non trivial solution i.e.
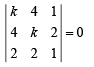
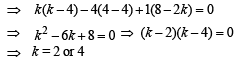
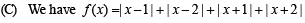
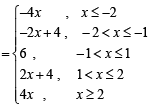
The graph of the above function is as given below
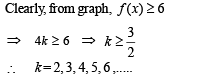
(D) Given that

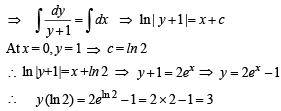
Q. 5. Match the statement in Column-1 with the values in Column -II
Column – I Column – II
(A) A line from the origin meets the lines 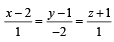 (p) – 4
(p) – 4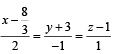 and at P and Q respectively..
and at P and Q respectively..
If length PQ = d, then d2 is
(B) The values of x satisfying (q) 0

(C) Non-zero vectors  (r) 4
(r) 4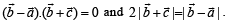
 , then the possible values of μ are
, then the possible values of μ are
(D) Let f be the function on [–π, π] given by f (0) = 9 (s) 5
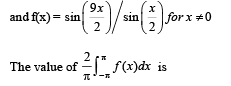
Ans. (A) → t; (B) → p, r; (C) → q, s; (D) → r
Solution. Let the line through origin be 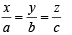 — (1)
— (1)
then as it intersects
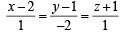 —(2)
—(2)
and 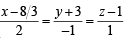 —(3)
—(3)
at P and Q, shortest distance of (1) with (2) and (3) should be zero.
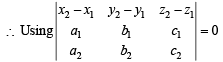
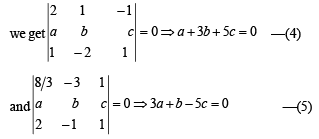
Solving (4) and (5), we get
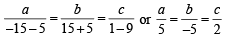
Hence equation (1) becomes 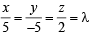
For some value of 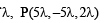
which lies on (2) also
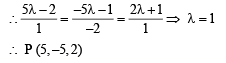
Also for some value of 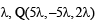
which lies on (3) also
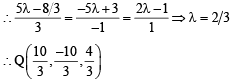
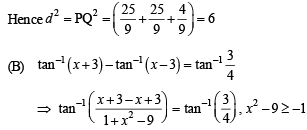

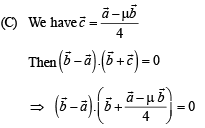
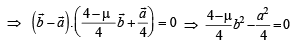
From (1) and (2), we get
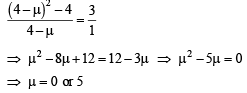
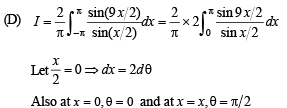
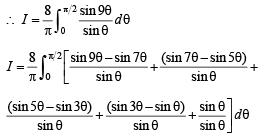
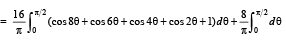
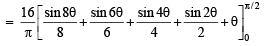
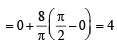
Q. 6. Match the statements given in Column-I with the values given in Column-II.
Column-I Column-II
(A) 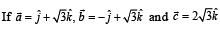 form (p) π/6
form (p) π/6
a triangle, then the internal angle of the triangle
between 
(B) 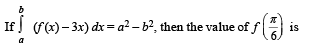 (q) 2π/3
(q) 2π/3
(C) The value of 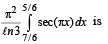 (r) π/3
(r) π/3
(D) The maximum value of 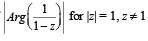 (s) π
(s) π
is given by
(t) π/2
Ans. A→q, B→p, C→s, D→t
Solution. 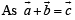
∴ The figure is as shown.
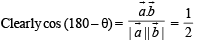
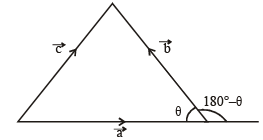
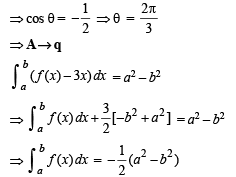
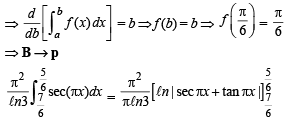
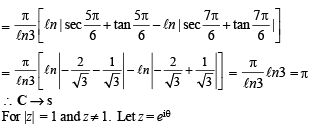
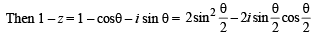
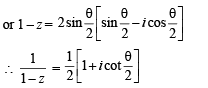
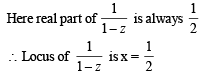
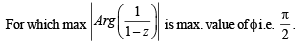
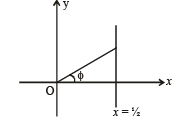
Clearly max.  but will not be attained.
but will not be attained.
∴ D → t.
|
347 docs|185 tests
|
|
347 docs|185 tests
|

|
Explore Courses for JEE exam
|

|

















