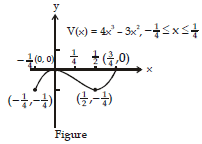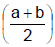Maxima and Minima of a Function | Mathematics (Maths) for JEE Main & Advanced PDF Download
MAXIMA AND MINIMA
A. Classification of Maxima & Minima
A function f(x) is said to have a local maximum at x = a if f(a) is greater than every other value assumed by f(x) in the immediate neighbourhood of x = a . Symbolically
⇒ x = a gives local maxima for a sufficiently small positive h .
Similarly, a function f(x) is said to have a local minimum value at x = b if f(b) is least than every other value assumed by f(x) in the immediate neighbourhood at x = b . Symbolically if
⇒ x = b gives local minima for a sufficiently small positive h .
Note that :
(i) The local maximum & minimum values of a function are also known as relative maxima or relative minima as these are the greatest & least values of the function relative to some neighbourhood of the point in question .
(ii) The term 'extremum' or 'turning point' is used both for local maximum or minimum values.
(iii) A local maximum (minimum) value of a function may not be the greatest (least) value in a finite interval.
(iv) A function can have several local maximum & minimum values & a local minimum value may even be greater than a local maximum value.
B. Fermat's Theorem
If f(x) has a local maximum or minimum at x = c and if f ' (c) exists, then f ' (c) = 0 .
(i) The set of values of x for which f ' (x) = 0 are often called as stationary points. The rate of change of function is zero at a stationary point.
(ii) In case f ' (c) does not exist, f(c) may be a maximum or a minimum.
C. The First Derivative Test
Suppose that c is a critical number of a continuous function f.
(a) If f' changes from positive to negative at c, then f has a local maximum at c.
(b) If f' changes from negative to positive at c, then f has a local minimum at c.
(c) If f' does not change sign at c (for example, if f' is positive on both sides of c or negative on both sides), then f has no local maximum or minimum at c.
In part (a), since the sign of f'(x) change from positive to negative at c, f is increasing to the left of c and decreasing to the right of c. It follows that f has local maximum at c.
It is easy to remember the First Derivative Test by visualizing the following diagrams.
Sufficient conditions for an extremum
If x0 is a critical point of the function f(x) and the inequalities f'(x0 - h) > 0, f'(x0 + h) < 0 are satisfied for an arbitrary, sufficiently small h > 0, then the function f(x) possesses a maximum at the point x0; now if f'(x0 + h) < 0, f'(x0 + h) > 0, then the function f(x) possesses a minimum at the point x0. If the signs of f'(x0 + h) and f'(x0 + h) are the same, then the function f(x) does not possess an extremum at the point x0.
Ex.1 Test the function y = (x - 2)2/3 (2x + 1) for extremum.
Sol. We find y' =
The critical points are x = 1 (the derivative is zero) and x = 2 (the derivative does not exist). The inequalities y'(1 - h) > 0, y'(1 + h) < 0, y'(2 - h) < 0, y' (2 + h) > 0 hold at a sufficiently small h > 0. Consequently, at the point x = 1 the function possesses a maximum ymax = 3 and at the point x = 2 it possesses a minimum ymin = 0.
Ex.2 Let f(x) = . Then find the value of `a' for which f(x) has local minimum at x=2.
Sol. We have f(x) =
f(x) has local minima at x = 2. Since, f(x) = 2x - 3 for x
2 (is strictly increasing)
a2 – 9a – 10 ≥ 0 ⇒ (a + 1) (a – 10) ≥ 0 ⇒ a ≤ –1 or a ≥ 10
Ex.3 Find the local maximum and minimum values of the function
Sol. To find the critical number of g, we differentiate : g'(x) = 1 + 2 cos x
So g'(x) = 0 when cos x =
The solutions of this equation are 2π/3 and 4π/3.
Because g is differentiable everywhere, the only critical numbers are 2π/3 and 4π/3 and so we analyze g in the following table.
Because g'(x) changes from positive to negative at 2π/3, the First Derivative Test tells us that there is a local maximum at 2π/3 and the local maximum value is
Likewise, g'(x) changes from negative to positive at 4π/3 and so
Ex.4 Find the values of a for which all roots of the equation 3x4 + 4x3 - 12x2 + a = 0 are real and distinct.
Sol. Consider the function f(x) = 3x4 + 4x3 - 12x2 + a.
Then f'(x) = 12(x3 + x2 - 2x) = 12x (x - 1) (x + 2).
From the sign scheme for f'(x), we can see that the shape of the curve will be as shown alongside.
For four real and distinct roots, the two minima must lie below the X-axis and the maxima must lie above the x-axis.
Thus, we have f(–2) < 0 i.e. 48 – 32 – 48 + a < 0 ...(i) i.e. a < 32
and f(1) < 0 i.e. 3 + 4 – 12 + a < 0 ...
(ii) i.e. a < 5
and f(0) > 0 i.e. a > 0 ...(iii)
Taking intersection of inequalities (1), (2) and (3) we have a ∈ (0, 5).
Ex.5 If f(x) = x3 + 3(a - 7) x2 + 3(a2 - 9) x - 1. If f(x) attains maxima at some positive value of x, then find the possible values of a.
Sol. We have f(x) = x3 + 3 (a - 7)x2 + 3(a2 - 9) x - 1 and f '(x) = 3x2 + 6(a - 7) x + 3 (a2 - 9)
which shows that there are two critical points (real or imaginary). According to the given condition, there is one real critical point (maxima), then the other critical point must also be real (minima).
Also, we have f(-∞) = -∞ and f(∞) = ∞
From the above facts, the graph of the curve y = f(x) can be drawn as shown alongside. Thus, if maxima occurs at some +ve value of x, then the minima must also occur at some +ve value of x(see fig.).
Thus, the roots of equation f '(x) = 0 are +ve and distinct, which is possible if discriminant > 0
i.e. (a – 7)2 > a2 – 9 i.e. –14 a + 58 > 0
i.e. a < 29/7 ...(1)
and product of the roots > 0
i.e. a2 – 9 > 0
i.e. a < –3 or a > 3 ...(2)
and sum of the roots > 0
i.e. a – 7 <0 i.e. a < 7 ...(3)
Drawing the number line for inequalities (1), (2), (3) and taking intersection, gives
Ex.6 For what real values of a and b are all the extrema of the function; f(x) = a2x3 - 0.5 a x2 - 2x - b, is positive and the minimum is at the point x0 = 1/3.
Sol. For extrema, f'(x) = 0 ⇒
a2 – a – 6 = 0 ⇒ a = –2, 3
So their arises two cases as :
Case I : at a = 3, if function attains minimum and is positive,
Case II : at a = -2, if function attains minimum and is positive,
Ex.7 For what values of `a' the point of local minima of f(x) = x3 - 3ax2 + 3(a2 - 1)x + 1 is less than 4 and point of local maxima is greater than -2.
Sol. f'(x) = 3(x2 - 2ax + a2 - 1)
Clearly roots of the equation f'(x) = 0 must be distinct and lie in the interval (-2, 4)
D > 0 ⇒ a ∈ R ...(1)
f'(–2) > 2 ⇒ a2 + 4a + 3 > 0 ⇒ a < –3 or a > –1 ...(2)
f'(4) > 0 ⇒ a2 – 8a + 15 > 0 ⇒ a > 5 or a < 3 ...(3)
From (1), (2) and (3) - 1 < a < 3
Alternate : f'(x) = 3(x - (a - 1)) (x - (a + 1))
clearly - 2 < a + 1 < 4 and -2 < a - 1 < 4 ⇒ -1 < a < 3
D. Extremum at End-points
A point (c, f(c)) is called an endpoint of the graph of the function f if there exists an interval (a, b) containing c such that the domain of f contains every number of the interval (a, c) and no number of the interval (c, b), or vice versa.
If (c, f(c)) is an endpoint of the graph of f such that f(c) is the maximum or minimum value of in some interval containing c, then f(c) is called an endpoint extremum of f. Note the difference between this definition and that of a relative extremum, in which it is assumed that some open interval containing c is contained in the domain of the function.
Consider f(x) = . Clearly, f(-2) = 0 and f(2) = 0 are endpoint extrema of f. Also, f(0) = 2 is a (relative) maximum value of f.
E. Second-Derivative Test For Extremum
Let c be a critical point of f in an open interval (a, b); that is, assume a < c < b and f'(c) = 0. Assume also that the second derivative f'' exists in (a, b). Then we have the following :
(a) If f'' is negative in (a, b), f has a relative maximum at c.
(b) If f'' is positive in (a, b), f has a relative minimum at c.
The two cases are illustrated in Figure
Proof. Consider case (a), f'' < 0 in (a, b). The function f' is strictly decreasing in (a, b). But f'(c) = 0, so f' changes its sign from positive to negative at c, as shown in Figure (a). Hence, f has a relative maximum at c. The proof in case (b) is entirely analogous.
If f'' is continuous at c, and if f''(c) 0, there will be a neighbourhood of c in which f'' has the same sign as f''(c). Therefore, if f'(c) = 0, the function f has a relative maximum at c if f''(c) is negative, and a relative minimum if f''(c) is positive. This test suffices for many examples that occur in practice.
Ex.8 Find all possible values of ' a ' for which the cubic f (x) = x3 + a x + 2 is non monotonic and has exactly one real root .
Sol. Note that
(i) for 3 real and distinct roots we have or f (x1) . f (x2) < 0 ⇒ f (x) is non monotonic in this case
(ii) for exactly one real root and monotonic the graph will be as shown. Here f ' (x)
0
(iii) for exactly one real root and non monotonic the graph will be as shown. Here f (x1) . f (x2) > 0
Now f (x) = x3 + a x + 2 ⇒ f ' (x) = 3 x2 + a
if a
0 , f (x) is always increasing .
Now let a < 0 f ' (x) = 0 ⇒ x =
f '' (x) = 6 x ; f '' > 0 ⇒ minima and f '' < 0 ⇒ maxima
for exactly one real root and non monotonic (case iii)
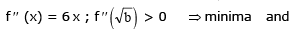
for exactly one real root and non monotonic (case iii)
Note that
(i) for a = - 3 , f (x) = x3 - 3 x + 2 = (x + 2) (x - 1)2 i.e. f (x) has two coincident roots .
(ii) for a < - 3 , f (x) has 3 real and distinct roots
(iii) for a
0 , f (x) is exactly real root and is always monotonic increasing find (x2 - x1)2 from (1) and get V as a function of y
Ex.9 Let 'p' & 'q' be real numbers . Prove that the cubic y = x3 + p x + q has three distinct real roots, if 4 p3 + 27 q2 < 0 .
Sol.
Let f (x) = x3 + p x + q ⇒ f'(x) = 3 x2 + p
If p > 0 ⇒ no root ( f (x) is monotonic)
3 distinct real roots f (x) must have exactly one maxima & minima .
Ex.10 Suppose f(x) is real valued polynomial function of degree 6 satisfying the following conditions ;
(a) f has minimum value at x = 0 and 2
(b) f has maximum value at x = 1
(c) for all x, = 2 .
Sol.
⇒ f(x) have co-efficient of x3, x2, x or constant term zero in order that the limit may exist.
Hence f(x) = ax6 + bx5 + cx4 ⇒ f'(x) = x3 (6 ax2 + 5 bx + 8)
f'(1) = 0 and f'(2) = 0 gives 6a + 5b + 8 = 0 and 24 a + 10 b + 8 = 0
F. GLOBAL MAXIMUM AND MINIMUM
Definition A function f has an absolute maximum (or global maximum) at c if f (c) ≥ f(x) for all x in D, where D is the domain of f. The number f(c) is called the maximum value of f on D. Similarly, f has an absolute minimum at c if f(c) ≤ f(x) for all x in D and the number f(c) is called the mini mum value of f on D. The maximum and minimum values of f are called the extreme values of f
Figure shows the graph of a function f with absolute maximum at d and absolute minimum at a. Note that (d, f(d)) is the highest point on the graph and (a, f(a)) is the lowest point.
The Extreme Value Theorem - Application Of Derivatives, Class 12, Maths
The Extreme Value Theorem
If f is continuous on a closed interval [a, b], then f attains an absolute maximum value f(c) and an absolute minimum value of f(d) at some numbers c and d in [a, b].
The Extreme Value Theorem is illustrated in Figure 1. Note that an extreme value can be attained at more than one point. Although the Extreme Value Theorem is intuitively very plausible, it is difficult to prove and so we omit the proof.
Conditions of Extreme Value Theorem
Figure 2, 3 show that a function need not possess extreme values if either hypothesis (continuity or closed interval) is omitted from the Extreme Value Theorem. The function f whose graph is shown in Figure 2 is defined on the closed interval [0, 2] but has no maximum value. (Notice that the range of f is [0, 3). The function takes on values arbitrarily close to 3, but never actually attains the value 3.) This does not contradict the extreme value theorem.
The function f shown in Figure 3 is continuous on the open interval (0, 2) but has neither a maximum nor a minimum value. The range of g is (1, ∝). The function takes on arbitrarily large values.] This does not contradict the Extreme Value Theorem because the interval (0, 2) is not closed.
In each case, explain why the given function does not contradict the extreme value theorem.
a. The function f has no maximum. It takes on all values arbitrarily close to 2, but it never reaches the value 2. The extreme value theorem is not violated because f is not continuous on [0, 2].
b. Although the functional values of g(x) become arbitrarily small as x approaches 0, it never reaches the value 0, so g has no minimum. The function g is continuous on the interval (0, 2], but the extreme value theorem is not violated because the interval is not closed.
Procedure for Finding the Extrema of a Continuous Function
Suppose a continuous function f is differentiable at all except a finite number of values of x in its domain, the closed interval
1. Find all x in a < x < b that satisfy the equation f'(x) = 0 or at which f'(x) does not exist; let x = r, x = s, x = t, .... be such x. The numbers r, s, t, . . . are often called critical points of f.
2. Evaluate f at each critical point; that is, find f(r), f(s), f(t),........
3. Evaluate f(a) and f(b).
4. The largest of the numbers computed in Step 2 and Step 3 is the maximum of f(x) for a £ x £ b, and the smallest number is the minimum.
Ex.11 Let f(x) = 2x3 - 9x2 + 12x + 6. discuss the global maxima and global minima of f(x) in (1, 3).
Sol.
f(x) = 2x3 – 9x2 + 12x + 6 ⇒ f'(x) = 6x2 – 18x + 12 ⇒ f'(x) = 6 (x – 1) (x – 2)
let f'(x) = 0 ⇒ x = 1, 2. ∴ f(1) = 11 and f(2) = 10 ...(i)
let us consider the open interval (1, 3). Clearly x = 2 is the only point in (1, 3) and f(2)=10 [from (i)
Thus, x = 2 is the point of global minima in (1, 3) and global maxima does not exist in (1, 3).
Ex.12 Let w(x) = 4x2 - 3x2 on - < x <
. Discuss the extrema of w.
Sol. w(x) has a maximum at x = 0 and a minimum at x = 1/2 , and these two values are in the given interval.
Ex.13 The greatest value of the function f(x) = in the interval [- 1, 1] is
Sol. f'(x) = 2.3x . l n 3 [ 3.32x - 4.3 x + 2 ]
Hence f (x) is greatest when x = 1 & f (1) = 24
Ex.14 Let f (x) = ax2 - 4ax + b (a > 0) be defined in Suppose the average of the maximum value and the minimum value of the function is 14, and the difference between the maximum value and minimum value is 18. Find the value of a2 + b2.
Sol.
f (x) = ax2 – 4ax + b (a > 0) ⇒ f ' (x) = 2ax – 4a = 0
at x = 2 also, f ' (x) = 2a(x – 2) ⇒ for x ∈ (1, 2) f is
Hence minimum occurs as x = 2
f (2) = 4a – 8a + b
f(2) = b – 4a
maximum will occur at f (5) and
M – m = 9a = 18 ⇒ a = 2 also M+m/2 = 14 ⇒ M + m = 28 = 2b + a ⇒ b = 13
Hence a = 2 and b = 13
a2 + b2 = 4 + 169 = 173
Ex.15 If f(x)= and f(x) = 0 has both non-negative roots, then prove that
Sol. Given that f(x) = (x - a) (x - b) -
Sum of the root of the equation f(x) = 0, will be positive ⇒ (a + b) > 0
The product of the roots of the equation will be greater than and equal to zero
Now f(x) will be minimum, when f'(x) = 0 ⇒ x =a+b/2
Ex.16 If x > 0, let f(x) = 5 x2 + A x -5 , where A is a positive constant . Find the smallest A such that for all x > 0 .
Sol.
f ' (x) = 10 x - 5 A x -6 and f '' (x) = 10 + 30 A x -7 > 0 i.e. f ' (x) = 0 gives a minima
Since A > 0 ⇒ we get only one minima and no maxima . Hence smallest value of f(x) will be at
Ex.17 Find the sum of the local maximum and local minimum values of the function f (x) =
Sol.
⇒ (t – 3t2)y = 3 – t , 3yt2 – (1 + y)t + 3 = 0
t > 0 ⇒ D ≥ 0 ; Sum of roots > 0 ; Product of roots >
hence (1 + y)2 – 36y ≥ 0;
⇒ y2 – 34y – 1 ≥ 0 ⇒ (y – 17)2 ≥ 288
⇒ (y – 17 – 12√2 )(y – 17 + 12√2 ) ≥ 0
⇒ [y – (17 + 12√2 )] [y – (17 – 12√2 )] ≥ 0
Hence ymax = 17 – 12√2 , ymin = 17 + 12√2 ⇒ ymax + ymin = 34 which is rational
Ex.18 For a certain curve = 6x - 4 and y has a local maximum value 5 when x = 1 . Find the equation and the global maximum and minimum values of y, given that
Sol.
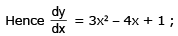
Integrating again, y = x3 - 2x2 + x + B ; y]x = 1 ⇒ B = 5.
Thus y = x3 - 2x2 + x + 5.
given x = 1/3 and z = 1 f(1/3) =139/27; f(1) = 5
also f(0) = 5 ; f(2) = 7 . Hence GMV = 7 ; gmv = 5
Ex.19 Find the least and the greatest value of f(x, y) = x2 + y2 - xy where x and y are connected by the relation x2 + 4y2 = 4.
Sol.
Here x2 + 4y2 = 4
⇒
⇒ Let x = 2 cos θ, y = sinθ
Hence, f(x, y) = x2 + y2 – xy = 4 cos2θ + sin2θ –2 sinθ cosθ = 2 (1 + cos 2θ) + 1/2 (1 - cos 2θ) - sin2θ
“Since we know a sinθ + b cosθ lies between
Thus, greatest value of f(x, y) =
and least value of f(x, y)
G. Geometrical Problems
Working Rule
1. When possible , draw a figure to illustrate the problem & label those parts that are important in the problem . Constants & variables should be clearly distinguished.
2. Write an equation for the quantity that is to be maximized or minimized . If this quantity is denoted by `y' , it must be expressed in terms of a single independent variable x . This may require some algebraic manipulations.
3. If y = f (x) is a quantity to be maximum or minimum, find those values of x for which f '(x) = 0 or f'(x) does not exist.
4. Test each value of x to determine whether it provides a maximum or minimum or neither. The usual tests are:
(a) If d²y/dx² is positive when dy/dx = 0 ⇒ y is minimum.
If d²y/dx² is negative when dy/dx = 0 ⇒ y is maximum.
If d²y/dx² = 0 when dy/dx = 0, the test fails.
(b) ⇒ a maximum occurs at x = x0.
But if dy/dx changes sign from negative to zero to positive as x advances through xo there is a minimum. If dy/dx does not change sign, neither a maximum nor a minimum.
5. If the function y = f (x) is defined for only a limited range of values then examine x = a & x = b for possible extreme values.
Useful Formulae Of Mensuration
- Volume of a cuboid = lbh .
- Surface area of a cuboid = 2 (lb + bh + hl) .
- Volume of a prism = area of the base x height .
- Lateral surface of a prism = perimeter of the base x height .
- Total surface of a prism = lateral surface + 2 area of the base (Note that lateral surfaces of a prism are all rectangles) .
- Volume of a pyramid = 1/3 area of the base x height .
- Curved surface of a pyramid = 1/2 (perimeter of the base) x slant height .
- (Note that slant surfaces of a pyramid are triangles) .
- Volume of a cone = 1/3πr2h
- Curved surface of a cylinder = 2 πrh .
- Total surface of a cylinder = 2πrh + 2πr2
- Volume of a sphere = 4/3πr3
- Surface area of a sphere = 4πr2
- Area of a circular sector = 1/2r2 θ, when θ is in radians.
Ex.20 A trapezium ABCD is inscribed into a semicircle of radius l so that the base AD of the trapezium is a diameter and the vertices B & C lie on the circumference . Find the base angle q of the trapezium ABCD which has the greatest perimeter .
Sol. Hint : P = AB + BC + CD + DA = (AB + CD) + BC + DA
CD = AB = 2 l cos θ ; AD = 2 l and
x = AB cos θ ⇒ BC = 2 l - 2 x = 2 l - 2 AB cosθ = 2 l - 4 l cos2θ
Hence P = 4 l + 4 l cosθ - 4 l cos2 θ
Ex.21 A bus contractor agrees to run special buses for the employees of ABC Co. Ltd . He agrees to run the buses if atleast 200 persons travel by his buses . The fare per person is to be Rs. 10/- per day if 200 travel and will be decreased for everybody by 2 praise per person over 200 that travels . How many passengers will give the contractor maximum daily revenue ?
Sol. Let number of passengers be x, which will yield maximum profit
⇒ f'(x) = 0 ⇒ x = 350 ; f(x)]max = 2450
Ex.22 Find the radius of the smallest circular disk large enough to cover every isosceles triangle of a given perimeter L.
Sol.
Ex.23 Through a point A on the circumference of a circle of radius r, two straight lines are drawn enclosing an angle f . If the straight lines meet the circle again at B & C, find the maximum area of triangle ABC .
Sol.
A = 2r2 sin ø sin ø sin (θ +ø) = r2 sinø [ cosø- cos (2θ +ø) ]
Ans. : r2 sin ø (1 + cosø) sq. units
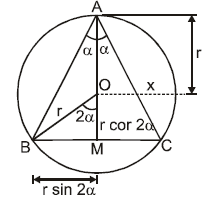
Ex.24 An isosceles triangle is inscribed in a circle of radius r . If the angle 2 α at the apex is restricted to lie between find the largest and the smallest value of the perimeter of the triangle . Give sufficient details of your reasoning .
Sol.
P = f (α) = 4 r (1 + sin α) cos α
f'(α) = 4 r [ cos2 α - (1 + sin α) cos α] = 4 r (1 - 2 sin α) (1 + sin α)
Ex.25 The plan view of a swimming pool consists of a semicircle of radius r attached to a rectangle of length '2r' and width 's' . If the surface area A of the pool is fixed, for what value of 'r' and 's' the perimeter 'P' of the pool is minimum .
Sol.
Ex.26 Find the altitude of a cone of the least volume that can be drawn around a hemisphere of radius R (the centre of the base of the cone falls on the centre of the sphere).
Sol.
Let AO = H, BO = r = radius of the base of the cone
R = radius of the hemisphere, ∠OAC = θ (θ ∈(0, π/2))
Clearly V(θ) has only one critical point namely θ = sin-1 1/√3 .Using sign scheme for V'(θ)
we get, θ = sin-1 1/√3 to be the point of maxima. Hence corresponding altitude H R/sinθ = R√3 .
Ex.27 What normal to the curve y = x2 forms the shortest chord.
Sol. Let (t, t2) be any point on the parabola y = x2
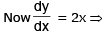
So, the slope of the normal to y = x2 at (t, t2) is (-1/2t)
The equation of the normal to y = x2 at (t, t2) is y – t2 =(-1/2t) (x-t)....(1)
Suppose equation (i) meets the curve again at B(t1, t12), then,
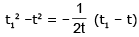
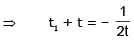
Let L be the length of the chord AB (as normal)
L = AB2 = (t – t1)2 + (t2 – t12)2 = (t – t1)2 [1 + (t + t1)2]
⇒ equation of normal AB is √2 x + 2y – 2 = 0 and √2 x – 2y + 2 = 0
Ex.28 The circle x2 + y2 = 1 cuts the x-axis at P and Q. Another circle with centre at Q and variable radius intersects the first circle at R above the x-axis and the line segment PQ at S. Find the maximum area of the triangle QSR.
Sol. The centre of the circle x2 + y2 = 1 ....(i) is (0, 0) and radius OP=1=OQ so, co-ordinates of Q are (1, 0)
Let the radius of the variable circle be r. Hence, its equation is (x - 1)2 = (y)2 = r2 ...(ii)
Hence, area is maximum at
H. Maximum and Minimum for Discrete Valued Functions
Ex.29 Find the largest term in the sequence an =
Sol.
⇒ f(x) strictly increases in (0, √10 ) strictly decreases in ( 10 , ∝)
⇒ f(x) has greatest value at x = √10
Hence, the given sequence has greatest value at n = 3 or n = 4.
Now, we have a3 = 3/19 and a4 = 4/26. Hence, a3 = 3/19. is the largest term of the given sequence.
I. Concavity and Point of Inflection
The graph of the function y = f(x) is said to be concave down on the interval (a, b) if it lies below the tangent drawn at any point of that interval (Fig. 1).
The graph of the function y = f(x) is said to be concave up on the interval (a, b) if it lies above the tangent drawn at any point of that interval (Fig. 2).
The sufficient condition for the concavity of the graph of a function.
If f''(x) < 0 on the open interval (a, b) then the graph of the function is concave down on that interval; now if f''(x) > 0, then on the open interval (a, b) the graph of the function is concave up.
The point (x0; f(x0)) of the graph of the function separating its concave down part from the concave up part is called a point of inflection (Fig. 3).
If x0 is the abscissa of the inflection point of the graph of the function y = f(x), then the second derivative is equal to zero or does not exist. The points at which f''(x) = 0 or f''(x) does not exist are called critical points of the 2nd kind.
If x0 is a critical point of the 2nd kind and the inequalities f''(x0 - h) < 0, f''(x0 + h) > 0 (or inequalities f''(x0 - h) > 0, f''(x0 + h) < 0) hold for an arbitrary sufficiently small h > 0, then the point of the curve y = f(x) with the abscissa x0 is a point of inflection.
If f''(x0 - h) and f''(x0 + h) are of the same sign, then the point of the curve y = f(x) with the abscissa x0 is not a point of inflection.
Ex.30 Find the intervals of concavity of the graph of the function y = x5 + 5x - 6.
Sol. We have y' = 5x4 + 5, y'' = 20x3. If x < 0, then y'' < 0 and the curve is concave down ; now if x > 0, then y'' > 0 and the curve is concave up. Thus we see that the curve is concave down on the interval (-∞, 0) and concave up on the interval (0, + ∞).
Ex.31 Find the inflection points of the curve y = (x - 5)5/3 + 2.
Sol. We find
The second derivative does not vanish for any value of x and does not exist at x = 5. The value x = 5 is the abscissa of the inflection point since y'' (5 - h) < 0, y''(5 + h) > 0. Thus, (5, 2) is the inflection point. Inflection points can also occur if
fails to exist .
Cusp :
A point on a graph where the curve makes an abrupt change in direction is called a cusp. Our next example features a graph with such a point.
Find the first and second derivatives and write them in factored form.
Let f(x) = 2x5/3 + 5x2/3.
Note that the graph is concave down on both sides of x = 0 and that the slope f'(x) decreases without bound to the left of x = 0 and increases without bound to the right. This means the graph changes direction abruptly at x = 0, and we have a cusp at the origin.
Ex.32 Prove that for any two numbers x1 & x2
Sol.
Assume f(x) = ex and let x1 & x2 be two points on the curve y = ex.
Let R be another point which divides P and Q in ratio 1 : 2.
y coordinate of point R is
and y coordinate of point S is
.Since f(x) = ex is always concave up, hence point R will always be above point S
(above inequality could also be easily proved using AM and GM.)
Ex.33 If 0 < x1 < x2 < x3 < then prove that sin
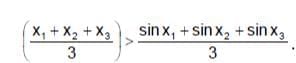 . Hence or otherwise prove that if A, B, C are angles of triangle then maximum value of sinA + sin B + sin C is
. Hence or otherwise prove that if A, B, C are angles of triangle then maximum value of sinA + sin B + sin C is
Sol.
Let point A, B, C form a triangle y coordinate of centroid G is
and y coordinate of point F is
If A + B + C = π , then
⇒ maximum value of (sin A + s in B + s in C)
|
172 videos|503 docs|154 tests
|
FAQs on Maxima and Minima of a Function - Mathematics (Maths) for JEE Main & Advanced
| 1. What is the definition of Maxima and Minima of a function? |  |
| 2. How do you find the Maxima and Minima of a function? |  |
| 3. What is the second derivative test? |  |
| 4. What is the difference between a local and a global Maxima or Minima? |  |
| 5. Can a function have multiple Maxima or Minima? |  |