Mean, median & mode | Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE) PDF Download
Mean, Median, and Mode?
Mean, median, and mode are measures of central tendency used in statistics to summarize a set of data.- Mean (x̅ or μ): The mean, or arithmetic average, is calculated by summing all the values in a dataset and dividing by the total number of values. It’s sensitive to outliers and is commonly used when the data is symmetrically distributed.
- Median (M): The median is the middle value when the dataset is arranged in ascending or descending order. If there’s an even number of values, it’s the average of the two middle values. The median is robust to outliers and is often used when the data is skewed.
- Mode (Z): The mode is the value that occurs most frequently in the dataset. Unlike the mean and median, the mode can be applied to both numerical and categorical data. It’s useful for identifying the most common value in a dataset.
What is Mean?
Mean is the sum of all the values in the data set divided by the number of values in the data set. It is also called the Arithmetic Average. Mean is denoted as x̅ and is read as x bar.The formula to calculate the mean is:
 Formula of Mean
Formula of MeanMean Symbol
The symbol used to represent the mean, or arithmetic average, of a dataset is typically the Greek letter “μ” (mu) when referring to the population mean, and “x̄” (x-bar) when referring to the sample mean.
- Population Mean: μ (mu)
- Sample Mean: x̄ (x-bar)
These symbols are commonly used in statistical notation to represent the average value of a set of data points.
Mean Formula
The formula to calculate the mean is:
If x1, x2, x3,……, xn are the values of a data set then the mean is calculated as:
x̅ = (x1 + x2 + x3 + . . . + xn) / n
Solved Example: Find the mean of data sets 10, 30, 40, 20, and 50.
Solution:
Mean of the data 10, 30, 40, 20, 50 is
Mean = (sum of all values) / (number of values)
Mean = (10 + 30 + 40 + 20+ 50) / 5 = 30
What is Median?
A Median is a middle value for sorted data. The sorting of the data can be done either in ascending order or descending order. A median divides the data into two equal halves.The formula to calculate the median of the number of terms if the number of terms is even is shown in the image below:
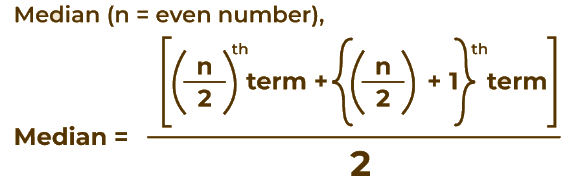 Median Formula for Even Terms
Median Formula for Even TermsThe formula to calculate the median of the number of terms if the number of terms is odd is shown in the image below:
 Median Formula for Odd Terms
Median Formula for Odd Terms
Median Symbol
The letter “M” is commonly used to represent the median of a dataset, whether it’s for a population or a sample. This notation simplifies the representation of statistical concepts and calculations, making it easier to understand and apply in various contexts. Therefore, in Indian statistical practice, “M” is widely accepted and understood as the symbol for the median.
Median Formula
The formula for the median is:
If the number of values (n value) in the data set is odd then the formula to calculate the median is:
If the number of values (n value) in the data set is even then the formula to calculate the median is:
Solved Example: Find the median of given data set 30, 40, 10, 20, and 50.
Solution:
Median of the data 30, 40, 10, 20, 50 is,
Step 1: Order the given data in ascending order as:
10, 20, 30, 40, 50
Step 2: Check n (number of terms of data set) is even or odd and find the median of the data with respective ‘n’ value.
Step 3: Here, n = 5 (odd)
Median = [(n + 1)/2]th term
Median = [(5 + 1)/2]th term
= 30
What is Mode?
A mode is the most frequent value or item of the data set. A data set can generally have one or more than one mode value. If the data set has one mode then it is called “Uni-modal”. Similarly, If the data set contains 2 modes then it is called “Bimodal” and if the data set contains 3 modes then it is known as “Trimodal”. If the data set consists of more than one mode then it is known as “multi-modal”(can be bimodal or trimodal). There is no mode for a data set if every number appears only once.The formula to calculate the mode is shown in the image below:
 Formula of Median
Formula of MedianSymbol of ModeIn statistical notation, the symbol “Z” is commonly used to represent the mode of a dataset. It indicates the value or values that occur most frequently within the dataset. This symbol is widely utilised in statistical discourse to signify the mode, enhancing clarity and precision in statistical discussions and analyses.
Mode Formula
Solved Example: Find the mode of the given data set 1, 2, 2, 2, 3, 3, 4, 5.
Solution:
Given set is {1, 2, 2, 2, 3, 3, 4, 5}
As the above data set is arranged in ascending order.By observing the above data set we can say that,
Mode = 2
As, it has highest frequency (3)
Relation between Mean Median Mode
For any group of data, the relation between the three central tendencies mean, median, and mode is shown in the image below: Mode = 3 Median – 2 Mean
Mode = 3 Median – 2 MeanMean, Median and Mode: Another name for this relationship is an empirical relationship. When we know the other two measures for a given set of data, this is used to find one of the measures. The LHS and RHS can be switched to rewrite this relationship in various ways.
What is Range?
In a given data set the difference between the largest value and the smallest value of the data set is called the range of data set. For example, if height(in cm) of 10 students in a class are given in ascending order, 160, 161, 167, 169, 170, 172, 174, 175, 177, and 181 respectively. Then range of data set is (181 – 160) = 21 cm.Range of Data
Range is the difference between the highest value and the lowest value. It is a way to understand how the numbers are spread in a data set. The range of any data set is easily calculated by using the formula given in the image below: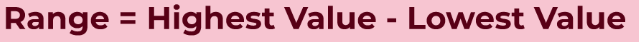
Range Formula
The formula to find the Range is:
Solved Example: Find the range of the given data set 12, 19, 6, 2, 15, 4.
Solution:
Given set is {12, 19, 6, 2, 15, 4}
Here,
Lowest Value = 2
Highest Value = 19Range = 19 − 2 = 17
Difference Between Mean and Median
The key differences between mean and median are listed in the following table: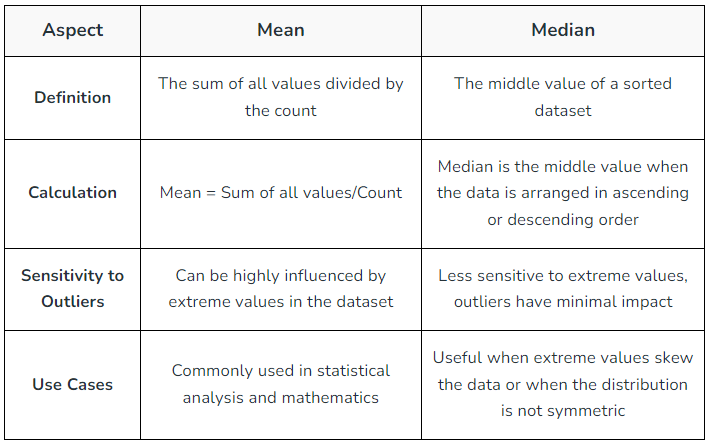
Differences between Mean, Median and Mode
Mean, median, and mode are measures of central tendency in statistics.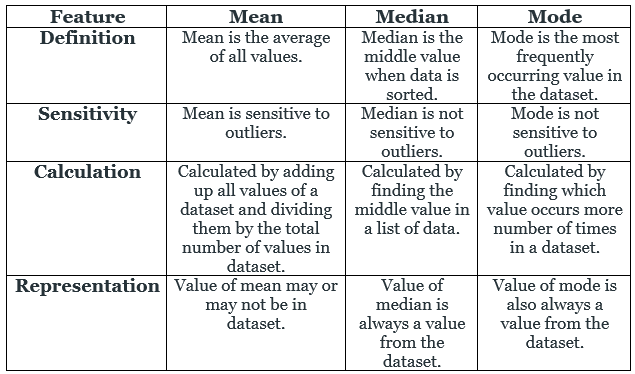
Difference Between Mean and Average
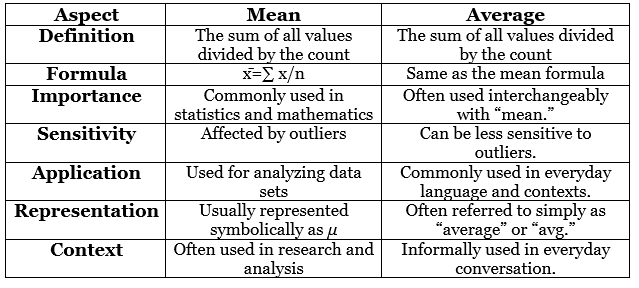
The terms “mean” and “average” are frequently used in mathematics and statistics, often interchangeably. However, they possess subtle distinctions in their meanings and applications.
Mean, in statistical terms, represents the arithmetic average of a dataset. It is calculated by summing up all the values in the dataset and dividing the sum by the total number of values. For instance, if you have the numbers 2, 4, 6, 8, and 10, the mean would be (2 + 4 + 6 + 8 + 10) / 5 = 6.
On the other hand, “Average” is a broader term that can refer to various measures of central tendency, including mean, median, and mode. In common usage, however, “average” often specifically denotes the mean. Like the mean, it involves summing up a set of values and dividing by the number of values to obtain a representative value.
Conclusion – Mean, Median, and Mode
Mean, median, and mode are essential measures of central tendency that help analyze and interpret data across various fields.Mean: Often used as the arithmetic average, it provides a quick summary of the data but is sensitive to extreme values or outliers. It is best used when the data is symmetrically distributed without extreme values.
Median: This measure represents the middle value of any dataset and is robust to outliers. It is particularly useful when dealing with skewed data distributions as it provides a better central value than the mean in such cases.
Mode: Indicating the most frequently occurring value, the mode is useful for identifying the most common value in a dataset. It can be applied to both numerical and categorical data, making it versatile for various types of analyses.
Together, these measures provide a comprehensive understanding of the central tendency in a dataset, enabling better decision-making and insights across different fields of study and applications.
Solved Numericals
Q1. Direction: Consider the following for the next two (02) items that follow.
The marks obtained by 60 students in a certain subject out of 75 are given below:
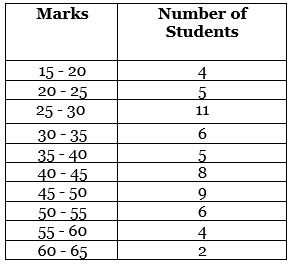
What is the mode?
Solution: Calculation:
From the table, we can see
Class with the highest frequency is 25 - 30 = modal class
Hence,
L = 25, f1 = 11, f0 = 5, f2 = 6, h = 5
Therefore,
Mode = 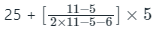
⇒ Mode = 27.73
∴ The required mode is 27.73
Q2. Direction: Consider the following for the next two (02) items that follow.
The marks obtained by 60 students in a certain subject out of 75 are given below:

What is the median?
Solution: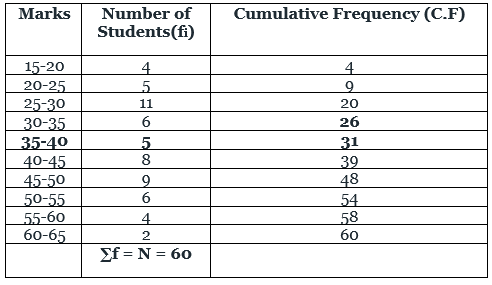
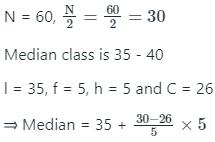
⇒ Median = 35 + 4 = 39
∴ Required median is 39.
Q3. What is the mean of the range, mode and median of the data given below?
5, 10, 3, 6, 4, 8, 9, 3, 15, 2, 9, 4, 19, 11, 4
Solution:
Given:
The given data is 5, 10, 3, 6, 4, 8, 9, 3, 15, 2, 9, 4, 19, 11, 4
Concept used:
The mode is the value that appears most frequently in a data set
At the time of finding Median
First, arrange the given data in the ascending order and then find the term
Formula used:
Mean = Sum of all the terms/Total number of terms
Median = {(n + 1)/2}th term when n is odd
Median = 1/2[(n/2)th term + {(n/2) + 1}th] term when n is even
Range = Maximum value – Minimum value
Calculation:
Arranging the given data in ascending order
2, 3, 3, 4, 4, 4, 5, 6, 8, 9, 9, 10, 11, 15, 19
Here, Most frequent data is 4 so
Mode = 4
Total terms in the given data, (n) = 15 (It is odd)
Median = {(n + 1)/2}th term when n is odd
⇒ {(15 + 1)/2}th term
⇒ (8)th term
⇒ 6
Now, Range = Maximum value – Minimum value
⇒ 19 – 2 = 17
Mean of Range, Mode and median = (Range + Mode + Median)/3
⇒ (17 + 4 + 6)/3
⇒ 27/3 = 9
∴ The mean of the Range, Mode and Median is 9
Q4. Find the mean of given data: Solution: Given:
Solution: Given: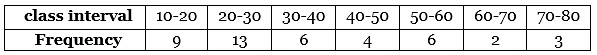
Calculation:
Now, to calculate the mean of data will have to find ∑fiXi and ∑fi as below,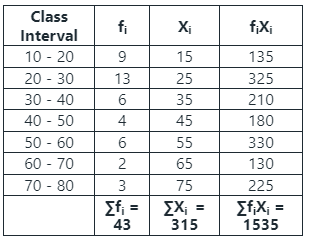 Then,
Then,
We know that, mean of grouped data is given by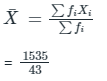
= 35.7
Hence, the mean of the grouped data is 35.7.
|
44 videos|109 docs|58 tests
|
FAQs on Mean, median & mode - Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE)
| 1. What is the mean in statistics? |  |
| 2. What is the median in statistics? |  |
| 3. What is the mode in statistics? |  |
| 4. What is the relationship between mean, median, and mode? |  |
| 5. What is the range in statistics? |  |
















