Mean & Variance of Random Variables | Applied Mathematics for Class 12 - Commerce PDF Download

Probability and Statistics: Mean of Random Variables

• Suppose you want to know or guess about your performance in the five mathematics tests. The total marks are the same for each of the tests. What can you say about your performance on the basis of the marks scored? What is your overall performance in these tests?
• You can do so by calculating the average of the marks obtained to get an idea of your overall performance. This average marks will tell you about the marks you are most close to.
• In probability and statistics, we can find out the average of a random variable. The term average is the mean or the expected value or the expectation in probability and statistics. Once we have calculated the probability distribution for a random variable, we can calculate its expected value. Mean of a random variable shows the location or the central tendency of the random variable.
• The expectation or the mean of a discrete random variable is a weighted average of all possible values of the random variable. The weights are the probabilities associated with the corresponding values. It is calculated as,
  E(X) = μ= Σ_i x_i p_i       i = 1, 2, …, n
  E(X) = x₁p₁ + x₂p₂ + … + x_np_n.

Properties of Mean of Random Variables

• If X and Y are random variables, then E(X + Y) = E(X) + E(Y).
• If X₁, X₂, … , X_n are random variables , then E(X₁ + X₂ + … + X_n) = E(X₁) + E(X₂) + … + E(X_n) = Σ_i E(X_i).
• For random variables, X and Y, E(XY) = E(X) E(Y). Here, X and Y must be independent.
• If a is any constant and X is a random variable, E[aX] = a E[X] and E[X + a] = E[X] + a.
• For any random variable, X > 0, E(X) > 0.
• E(Y) ≥ E(X) if the random variables X and Y are such that Y ≥ X.

Probability and Statistics: Variance of Random Variables

• Suppose you calculated the mean or the average marks in the five tests of mathematics. You can easily see the difference of marks in each of the tests from this average marks. This difference in marks shows the variability of the possible values of the random variable. The random variable being the marks scored in the test.
• The variance of a random variable shows the variability or the scatterings of the random variables. It shows the distance of a random variable from its mean. It is calculated as σ_x² = Var (X) = ∑_i (x_i − μ)² p(x_i) = E(X − μ)² or, Var(X) = E(X²) − [E(X)]².
• E(X²) = ∑_i x_i² p(x_i), and [E(X)]² = [∑_i x_i p(x_i)]² = μ².
• If the value of the variance is small, then the values of the random variable are close to the mean.

Properties of Variance of Random Variables

• The variance of any constant is zero i.e, V(a) = 0, where a is any constant.
• If X is a random variable, and a and b are any constants, then V(aX + b) = a² V(X).
• For any pair-wise independent random variables, X₁, X₂, … , X_n and for any constants a₁, a₂, … , a_n; V(a₁X₁ + a₂ X₂ + … +a_nX_n) = a₁² V(X₁) + a₂² V(X₂) + … + a_n² V(X_n).

Solved Example 

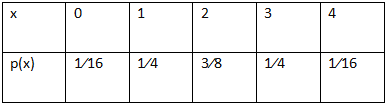
Example 1: Calculate the mean and variance for a random variable, X defined as the number of tails in four tosses of a coin. Also, draw the probability distribution.

Let T represents a tail and H, a head. X denotes the number of tails in four tosses of a coin. X takes the value 0, 1, 2, 3, 4.
P(X = 0) = 1⁄16, P(X = 1) = 4⁄16 = 1⁄4, P(X = 2) = 6⁄16 = 3⁄8, P(X = 3) = 4⁄16 = 1⁄4, P(X = 4) = 1⁄16
The probability distribution of X is
E(X) = Σ_i x_ip_i = 1 × 1⁄4 + 2 × 3⁄8 + 3 × 1⁄4 + 4 × 1⁄16 = 8⁄4 = 2.
E(X²) = 1² × ¼  + 2² × 3⁄8 + 3² × ¼ + 4² × 1⁄16 = ¼ + 3⁄2  + 9⁄4 + 1 = 5.
So, Variance of X = V(X) = E(X2) – [E(X)]² = 5 – 22 = 1.

Example 2: What is the meaning of probability in statistics?

Probability refers to the measuring of the probability that an event will happen in a Random Experiment. Probability is enumerated as a number between 0 and 1, where, loosely speaking, 0 denotes impossibility and 1 denotes certainty. The higher the likelihood of an event, the more prone it is that the event will take place.

Example 3: What is the relationship between probability and statistics?

Probability deals with forecasting the possibility of upcoming events, whereas statistics includes the analysis of the frequency of past events. Probability is mainly a theoretical branch of mathematics, which studies the results of mathematical definitions.

Example 4: What is the probability formula?

Probability Formulas equals to Probability = (Number of a Favorable outcome) / (Total number of outcomes) P = n (E) / n (S) Over here, P means the probability, E refers to the event and finally S refers to the sample space.

Example 5: What is the example of statistics?

Generally, we make use of a statistic to guess the value of a population parameter. For instance, the average height of the sampled students is a statistic. Thus, the same will be the average grade point average. In actual fact, any calculable quality of the sample will serve as an example of a statistic.