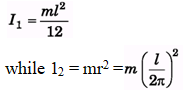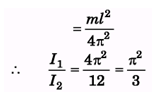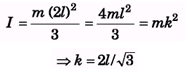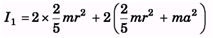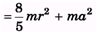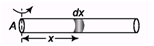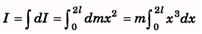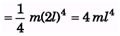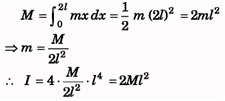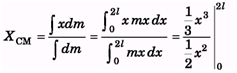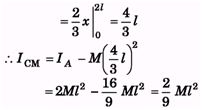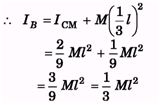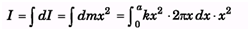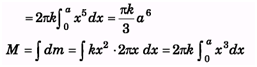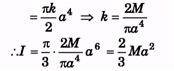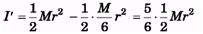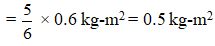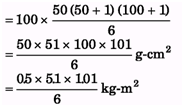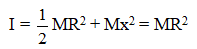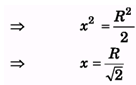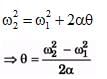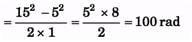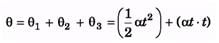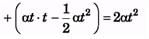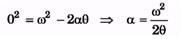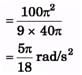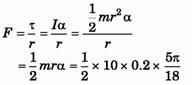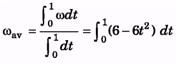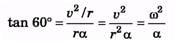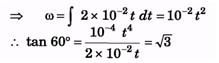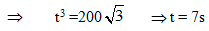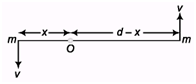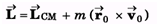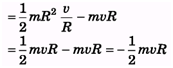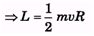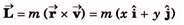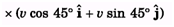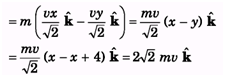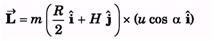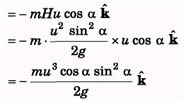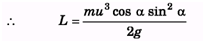DC Pandey Solutions: Mechanics of Rotational Motion | Physics Class 11 - NEET PDF Download
Introductory Exercise 9.1
Q.1. About what axis would a uniform cube have its minimum moment of inertia?
Ans. The mass distribution is at minimum separation from the diagonal passing through centre to opposite corners of the cube, so, moment of inertia is minimum about that axis.
Q.2. If I1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and I2 the moment of inertia of the ring formed by the same rod about an axis passing through the centre of mass of the ring and perpendicular to the plane of the ring. Then find the ratio 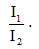
Ans.
Q.3. Find the radius of gyration of a rod of mass m and length 2l about an axis passing through one of its ends and perpendicular to its length.
Ans.
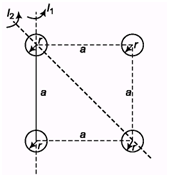
Q.4. There are four solid balls with their centres at the four corners of a
square of side a. The mass of each sphere is m and the radius is r. Find the moment of inertia of the system about (i) one of the sides of the square (ii) one of the diagonals of the square.
Ans.
(i)
(ii)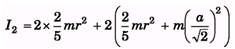
Q.5. A non-uniform rod AB has a mass M and length 2l. The mass per unit length of the rod is mx at a point of the rod distant x from A Find the moment of inertia of this rod about an axis perpendicular to the rod (a) through A (b) through the mid-point of AS.
Ans.
(a)
(b)
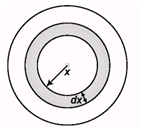
Q.6. A circular lamina of radius a and centre O has a mass per unit area of fkx2, where x is the distance from O and k is a constant. If the mass of the lamina is M, find in terms of M and a, the moment of inertia of the lamina about an axis through O and perpendicular to the lamina.
Ans.
Q.7. The uniform disc shown in the figure has a moment of inertia of 0.6 kg-m2 around the axis that passes through O and is perpendicular to the plane of the page. If a segment is cut out from the disc as shown, what is the moment of inertia of the remaining disc? 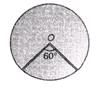
Ans.
Q.8. Particles of masses 1 g, 2 g, 3 g. ,.., 100 g are kept at the marks 1 cm, 2 cm, 3 cm, .,., 100 cm respectively on a metre scale. Find me moment of inertia of the system of particles about a perpendicular bisector of the metre scale.
Ans. I = (1 × 492 + 2 × 482 + 3 × 472 + ... + 49 × 12) + 50 × 02 + (100 × 502 + 99 × 492 + 98 × 482 +... + 51 × 1
= 100 × 502 +100 × 492 +...+ 100 × 12 = 100(12 +22 +32 +... + 502)
= 0.43 kg-m2
Q.9. (a) The radius of gyration of a uniform disc about a line perpendicular to the disc equals its radius R. Find the distance of the Sine from the centre. 10, If two circular disks of the same weight and thickness are made from metals having different densities.
(b) Which disk, if either will have the larger moment of inertia about its central axis.
Ans. (a)
(b) The disk with smaller density will have larger radius and as I = 1/2Mr2, so the disk with larger radius will have higher moment of inertia.
Introductory Exercise 9.2
Q.1. A body rotates about a fixed axis with an angular acceleration 1 rad/s2. Through that angle does it rotates during the time in which its angular velocity increases from 5 rad/s to 15 rad/s.
Ans.
Q.2. A wheel starting from rest is uniformly accelerated at 4 rad/s2 for 10 s. It is allowed to rotate uniformly for the next 10 s and is finally brought to rest in the next 10 s. Find the total angle rotated by the wheel.
Ans.
= 2 × 4 × 102 = 800rad
Q.3. A flywheel of moment of inertia 0.5 kg m2 is rotated at a speed of 10 rad/s. Because the fraction at the axis comes to rest in 10 s. Find the average torque of the friction.
Ans.
⇒τ = I α = 5 kg-m2 × 1 rad/s2 = 5 N-m
Q.4. A wheel of mass 10 kg and radius 0.2 m is rotating at an angular speed of 100 rpm when the motion is turned off. Neglecting the friction at the axis, calculate the force that must be applied tangentially to the wheel to bring it to rest in 10 rev. Assume the wheel to be a disc.
Ans.
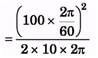
= 0.87 N
Q.5. A solid body rotates about a stationary axis according to the law q = 6t - 2t3. Here q is in radian and t in seconds. Find:
(a) the mean values of the angular velocity and angular acceleration averaged over the time interval between t = 0 and the complete stop,
(b) the angular acceleration at the moment when the body stops.
Hint If y = y(t), then mean/average value of y between t1 and t2 is 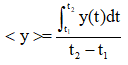
Ans.
θ = 6t – 2t3, ω = 6 – 6t2
⇒ω = 0 at t = 1 s
(a)
(b) α (1s) = -12t = -12 rad/s2
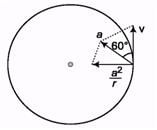
Q.6. A solid body starts rotating about a stationary axis with an angular acceleration a = (2.0 × 10-2)t rad/s2, here, t is in seconds. How soon after the beginnings of rotation will the total acceleration vector of an arbitrary point of the body form an angle θ = 60° with its velocity vector?
Ans.
dω = αdt
Introductory Exercise 9.3
Q.1. Two particles each of mass m and speed v, travel in opposite directions along parallel lines separated by a distance d. Show that the vector angular momentum of this system of particles is the same as any point taken as origin.
Ans.
L0 = mvx + mv (d - x) = mvd is a constant and is independent of x, i.e., position of O.
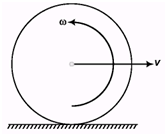
Q.2. In sample example, number 9.13 suppose the disc starts rotating anticlockwise with the same angular velocity ω = v/R, then what will be the angular momentum of the disc about the bottommost point in this new situation?
Ans.
= Iω + (- mvR)
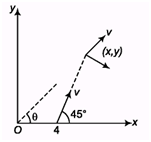
Q.3. A particle of mass m moves in xy plane along the line y = x – 4, with constant speed v. Find the angular momentum of particle about the origin at any instant of time t.
Ans.
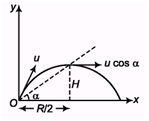
Q.4. A particle of mass m is projected from the ground with an initial speed u at an angle a. Find the magnitude of its angular momentum at the highest point of its trajectory about the point of projection.
Ans.
Q.5. If the angular momentum of a body is zero at about some point. Is it necessary that it will be zero at a different point?
Ans. It depends upon the distance, velocity and angle from the axis, which may not given zero from a different point.
Introductory Exercise 9.4
Ques 1: A thin circular ring of mass M and radius R is rotating about its axis with an angular speed ω0. Two particles each of mass m are now attached at diametrically opposite points. Find the new angular speed of the ring.
Ans:

Ques 2: If the ice at the poles melts and flows towards the equator, how will it affect the duration of day-night ?
Ans: As ice melts at pole and flows to equator, it gets distributed away from centre (as equitorial radius is greater than polar radius) such that moment of inertia about axis increases which results in decrease in angular speed (as Iω= constant), this leads in increase in time period  or duration of day and night.
or duration of day and night.
Introductory Exercise 9.5
Ques 1: In sample example 9.16, find the equation y(x)if at the initial moment the axis c of the disc was located at the point O after which it moved with a constant linear acceleration a0 (and the zero initial velocity) while the disc rotates counter clockwise with a constant angular velocity w.Ans:
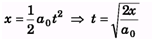
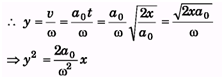
Ques 2. A uniform bar of length l stands vertically touching a wall OA. When slightly displaced, its lower end begins to slide along the floor. Obtain an expression for the angular velocity w of the bar as a function of q. Neglect friction everywhere.
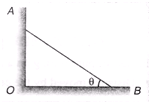
Ans:
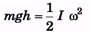
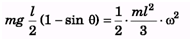
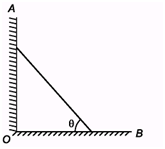
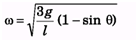
Introductory Exercise 9.6
Ques 1: A solid sphere of mass m rolls down an inclined plane a height h. Find rotational kinetic energy of the sphere. [Hint: Mechanical energy will remain conserved]Ans:
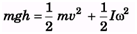
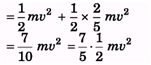
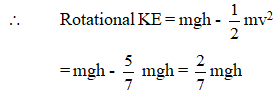
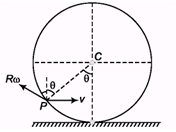
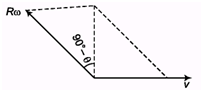
Ques 2: A ring of radius R rolls on a horizontal ground with linear speed v and angular speed ω. For what value of 8 the velocity of point P is in vertical direction, (v < R ω)
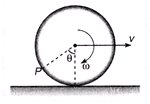
Ans;
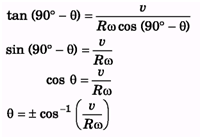
Ques 3: The topmost and bottommost velocities of a disc are v1 and v2 (< v1) in the same direction. The radius is R. Find the value of angular velocity ω.
Ans:
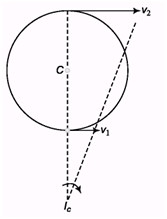
ωx = v1 and ω (x + 2R) = v2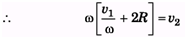
2Rω = v2 - v1
Introductory Exercise 9.7
Ques 1. A ball of mass M and radius R is released on a rough inclined plane of inclination q. Friction is not sufficient to prevent slipping. The coefficient of friction between the ball and the plane is m. Find:(a) the linear acceleration of the ball down the plane,
(b) the angular acceleration of the ball about its centre of mass.
Ans:
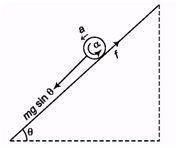
f = f2 = mN = mmg cos θ
(a) ma = mg sin θ - m mg cos θ
a = g (sin θ - m cos θ)
(b) Rf = Iα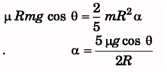
Ques 2. Work done by friction in pure rolling is always zero. Is this statement true or false?
Ans: Work done by friction is zero only in uniform pure rolling but not in accelerated pure rolling. So, the statement is false.
Ques 3. A spool is pulled by a force in vertical direction as shown in figure.
What is the direction of friction in this case? The spool does not loose contact with the ground.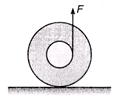
Ans: 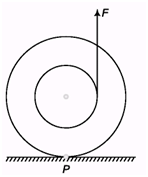
As the torque due to applied force is anti-clockwise, so the point of contact tries to slip rightwards and friction tries to prevent it and so acts leftwards.
Ques 4. A cylinder is rolling down a rough inclined plane. Its angular momentum about the point of contact remains constant. Is this statement true or false?
Ans: As during rolling down, friction acts upward which exerts a torque, thus the angular momentum of the system is not conserved. Even if we take axis of rotation at point of contact, then component of weight exerts torque, so, statement is false.
Ques 5. Two forces F1 and F2 are applied on a spool of mass M and moment of inertia I about an axis passing through its centre of mass. Find the ratio F1/F2 , so that the force of friction is zero. Given that I < 2Mr2.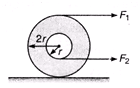
Ans: Force of friction will be zero, only when there is uniform pure rolling, i.e., there is no external unbalanced torque.
Thus, a = Rα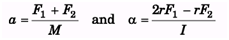
as, a = 2rα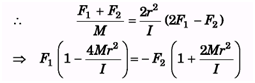
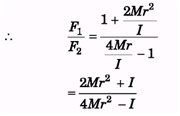
Ques 6. A disc is placed on the ground. Friction coefficient is m. What is the minimum force required to move the disc if it is applied at the topmost point?
Ans: 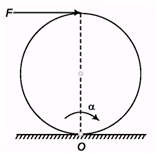
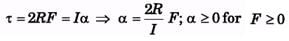
i.e., even a slightest amount of force can initiate motion of the disk.
Ques 7. When a body rolls, on a stationary ground, the acceleration of the point of contact is always zero. Is this statement true or false?
Ans: Acceleration of point of contact is zero only when there is uniform pure rolling and no slipping
Introductory Exercise 9.8
(a) cube slides before toppling?
(b) cube topples before sliding?
Ans:
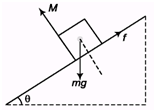
For sliding,
mg sin θ > μ mg cos θ
∴ tan θ > μ
And for toppling,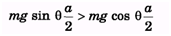
∴ tan θ > 1
(a) Cube will slide before toppling if tan θ < 1, i.e., μ < 1 and
(b) Cube will topple before sliding if tan θ > 1, i.e., μ > 1
Ques 2: A solid sphere of mass M and radius R is hit by a cue at a height h above the centre C. For what value of h the sphere will roll without slipping?
Ans: 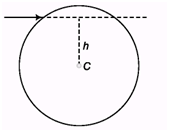
For rolling without slipping on horizontal plane, f = 0
Impulse, Im = Δp = mv Angular Impulse, Imh = ΔL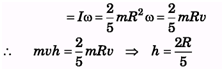
|
95 videos|367 docs|98 tests
|
FAQs on DC Pandey Solutions: Mechanics of Rotational Motion - Physics Class 11 - NEET
| 1. What are the key topics covered in DC Pandey Solutions: Mechanics of Rotational Motion JEE? |  |
| 2. How can DC Pandey Solutions help in preparing for the JEE exam? |  |
| 3. Are the solutions in DC Pandey Solutions: Mechanics of Rotational Motion JEE accurate and reliable? |  |
| 4. Can DC Pandey Solutions: Mechanics of Rotational Motion JEE be used for self-study and revision? |  |
| 5. How can DC Pandey Solutions: Mechanics of Rotational Motion JEE help in improving problem-solving skills for the JEE exam? |  |