Mensuration Class 8 Worksheet Maths Chapter 9
Multiple Choice Questions
Q1: The area of a parallelogram whose base is 9cm and altitude is 6cm
(a) 45cm2
(b) 54cm2
(c) 48cm2
(d) 84cm2
Ans: Area of parallelogram = base × altitude
= 9cm ×6cm = 54cm2
Therefore, correct option is (b)
Q2: The volume of a cube whose edge is 6a is
(a) 25a3
(b) 216a3
(c) 125a3
(d) None of these
Ans: Volume of cube = 6a3 = 216a3
Therefore, the correct option is (c)
Q3: The sum of the areas of all six faces of a cuboid is the _____ of the cuboid.
(a) Volume
(b) Surface area
(c) Area
(d) Curved surface area
Ans: Sum of the areas of all six faces of cuboid is the surface area of cuboid which is given by 2(l b + b h + h l)
Therefore, the correct option is (b)
Q4: The area of a. Rhombus is 240 cm2 and one of the diagonals is 16 cm Then other diagonal is
(a) 25cm
(b) 30cm
(c) 18cm
(d) 35cm
Ans: Area of Rhombus= 240cm2 = 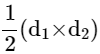
= 2×240cm2 = 16cm×d2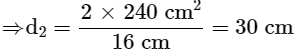
Therefore, correct option is (b)
Q5: The volume of water tank is 3m3. Its capacity in litres is
(a) 30
(b) 300
(c) 3000
(d) None of these
Ans: 1m3 = 1000litres
V = 3m3 = 3(1000) = 3000litres
Therefore, correct option is (c)
Fill in The Blanks
Q1: 10000 m2 = ________ hectare.
Ans: 1
Q2: 1 m2 = ________ cm2.
Ans: 10,000
Q3: Perimeter of a regular polygon = length of one side × ________.
Ans: number of sides
Q4: The distance around a circle is its ________.
Ans: circumference
Q5: If a wire in the shape of the square is rebent into a rectangle, then the ________ of both shapes remain same, but ________ may vary.
Ans: perimeter, their shapes
True(T) or False(F)
Q1: All the triangles that are equal in area are congruent.
Ans: False
Q2: All congruent triangles are equal in area.
Ans: True
Q3: Ratio of the circumference and the diameter of a circle is more than 3.
Ans: True
Q4: If the area of rectangle increases from 2 cm2 to 4 cm2, then perimeter will remains same.
Ans: False
Answer the following Questions
Q1: Find the area of a square, the length of the diagonal is √22m
Ans: Area of Square =  (∴d = 2√2m)
(∴d = 2√2m)
where d = diagonal length
Area of Square = 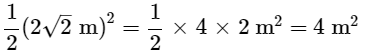
Q2: If the parallel sides of a parallelogram are 2cm apart and their sum is 12cm then find its area.
Ans: 
Opposite sides of a parallelogram are equal
∴ a + b = 12
a + a = 12
2a = 12
a = 6
Area of parallelogram = a×h = 6×2 = 12cm2
Q3: The length, breadth and height of a cuboid are 20cm, 15cm and 10cm respectively. Find its total surface area.
Ans:
L = 20cm , B = 15cm , H = 10cm
Surface area of cuboid = 2(lb + bh + hl)
= 2(20×15+15×10+10×20)cm2
= 2(300 + 150 + 200)cm2
= 2(650)cm2 = 1300cm2
Q4: Volume of Cube is 8000cm3. Find its surface area.
Ans:
V= 8000cm3
l3 = 8000cm3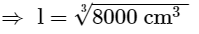
Surface Area of Cube = 6l2
= 6(20cm)2 = 2400cm2
Q5: Find the ratio of the areas of two circles whose radii is 7cm and 14cm.
Ans: r1 = 7cm
⇒ A1 = π(7)2 = 49π
r2 = 14cm
⇒ A2 = π(14)2 = 196π
A1:A2 = 49π:196π
A1:A2 = 7:28
Q6: Find the diameter of the circle whose circumference is 230m.
Ans: Circumference = 230m
2πr = 230m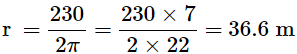
d = 2r = 2×36.6m = 73.18cm
Q7: Find the area of the figure if the upper portion is a semicircle Ans: Total area = Area of semicircle + Area of Rectangle
Ans: Total area = Area of semicircle + Area of Rectangle
Area of semicircle = 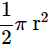
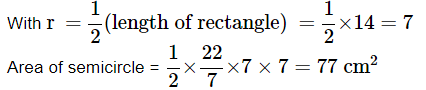
Area of rectangle = length × breadth
= 14×8 = 112cm2
Total area = (77 + 112)cm2 = 189cm2
Q8: A goat is tied to one corner of a square field of side 8mby a rope 3m long. Find the area it can graze? Also find the area the goat cannot graze.
Ans:
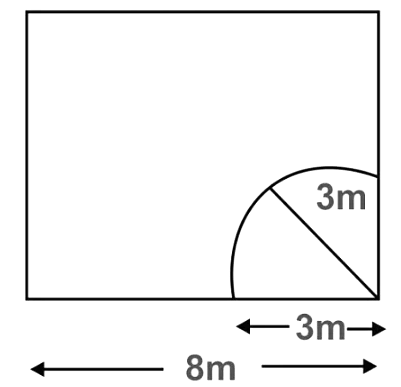
Length of side of a square = 8m
Area of square = (8m)2 = 64m2
Length of rope = 3m
= r (radius of circle)
As the goat is tied to a corner of square plot it can only graze 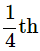 of circle of radius equal to length of of circle of radius equal to length of rope inside the plot.
of circle of radius equal to length of of circle of radius equal to length of rope inside the plot.
Area covered (or grazed) by goat = 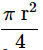
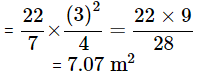
Area the goat cannot graze = Area of square – Area grazed by goat
= 64 - 7.07 = 56.93m2
Q9: If x units are added to the length of the radius of a circle, what is the number of units by which the circumference of the circle is increased?
Ans: Let the radius of the circle be ‘r’ units The circumference of the circle will be 2πr units
If the radius is increased by ‘x’ units, the new radius will be (r + x) units.
New circumference will be 2π(r + x) = 2πr + 2πx
Circumference increased by 2πx units.
Q10: Find the area of the shaded portion if diameter of circle is 16cm and ABCD is a square. Ans: Area of shaded portion = (Area of circle with radius =8cm) – (Area of square with diagonal length = 16cm)
Ans: Area of shaded portion = (Area of circle with radius =8cm) – (Area of square with diagonal length = 16cm)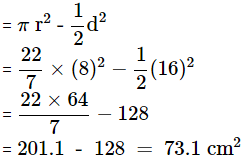
Q11: How many cm3 of juice can be poured in a cuboidal can whose dimensions are 15cm × 10cm × 25cm. How many cubical packs of 25cm3 volume can be made?
Ans: Volume of cuboid = Length × Breadth × Height
= 15cm×10cm×25cm
Volume of juice in cuboidal can = 3750cm3
Each volume of cubical packet = 25cm3
Number of such cubical packets made from the volume of juice in cuboidal can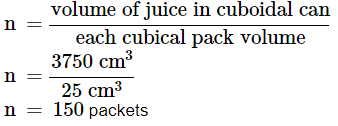
Q12: A rectangular piece of paper66 cm long and10cm broad is rolled along the length to form a cylinder. What is the radius of the base and calculate volume of cylinder?
Ans: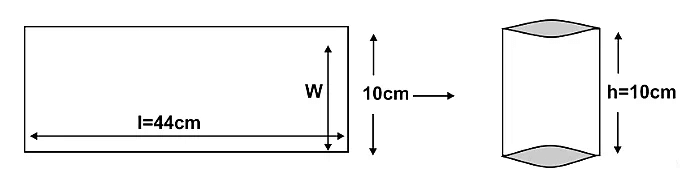
When the rectangular piece is rolled in the form of a cylinder then the length became the circumference of the base of cylinder
C = 66,
2πr = 66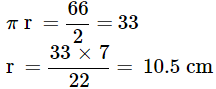
Volume of Cylinder with radius = 10.5cm and height = 10cm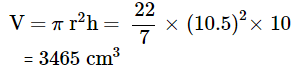
|
79 videos|408 docs|31 tests
|
FAQs on Mensuration Class 8 Worksheet Maths Chapter 9
| 1. What is mensuration? |  |
| 2. How is the area of a rectangle calculated? |  |
| 3. What is the formula for calculating the volume of a cylinder? |  |
| 4. How is the perimeter of a square calculated? |  |
| 5. How can I find the circumference of a circle? |  |


















