Mathematics Exam > Mathematics Notes > Mathematics for IIT JAM, GATE, CSIR NET, UGC NET > Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences
Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences | Mathematics for IIT JAM, GATE, CSIR NET, UGC NET PDF Download
Solution To Heat Equation by Separation of Variables and Eigenfunction and Expansion
We credit [2] for a second solution to the heat equation in a bounded domain x ∈ (0, l) for all time t > 0. If we are given initial conditions u(0, t) = u(l, t) = 0 and u(x, 0) = φ(x) then we can separate variables and write u as the product of one function of time only and one function of position only
Using the same method we used to solve the wave equation, we plug in this new function to the heat equation
and we find that both sides must equal a constant
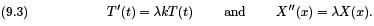
These are ordinary differential equations whose solutions are given by
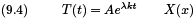
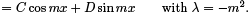
The boundary conditions imply D = 0 and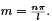 
We can find a general equation for u(x, t) by taking the in nite sum of all of the solutions
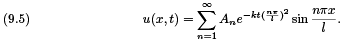
As in the case of the wave equation we can solve for the coeffcients by using our initial value function then using the same integration technique used in the solution to the wave equation.
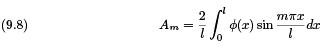
Acknowledgments. It is a pleasure to thank my mentors, Jessica Lin and Yan Zhang, for their help and guidance.
The document Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences | Mathematics for IIT JAM, GATE, CSIR NET, UGC NET is a part of the Mathematics Course Mathematics for IIT JAM, GATE, CSIR NET, UGC NET.
All you need of Mathematics at this link: Mathematics
|
556 videos|198 docs
|
FAQs on Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences - Mathematics for IIT JAM, GATE, CSIR NET, UGC NET
| 1. What is the wave equation? |  |
Ans. The wave equation is a second-order partial differential equation that describes the behavior of waves. It relates the second derivative of a function with respect to time to the second derivative of the same function with respect to position.
| 2. What is the method of separation of variables for the wave equation? | |
Ans. The method of separation of variables is a technique used to solve partial differential equations by assuming a solution that can be expressed as the product of two or more functions, each of which depends on only one variable. For the wave equation, this method involves assuming a solution of the form u(x,t) = X(x)T(t) and then substituting it into the equation to obtain two separate ordinary differential equations.
| 3. How does the method of separation of variables work for the wave equation? | |
Ans. In the method of separation of variables for the wave equation, we assume a solution of the form u(x,t) = X(x)T(t). By substituting this into the wave equation and dividing both sides by X(x)T(t), we obtain two separate ordinary differential equations: one involving only X(x) and the other involving only T(t). These equations can then be solved individually, and their solutions can be combined to obtain the general solution for u(x,t).
| 4. What are the boundary and initial conditions in the context of the wave equation? | |
Ans. In the context of the wave equation, boundary conditions refer to the conditions imposed on the solution u(x,t) at the boundaries of the domain. These conditions can specify the values of u(x,t), its derivatives, or a combination of both at the boundaries. Initial conditions, on the other hand, refer to the conditions imposed on the solution u(x,t) at a specific initial time, usually denoted as t=0. These conditions can specify the values of u(x,t), its derivatives, or a combination of both at different points in the domain at the initial time.
| 5. What are the main applications of the wave equation? | |
Ans. The wave equation has various applications in different fields. In physics, it is used to describe the behavior of waves in different mediums, such as sound waves, electromagnetic waves, and water waves. It is also used in engineering to analyze the vibrations of structures and the propagation of signals in communication systems. Additionally, the wave equation is employed in acoustics, seismology, optics, and many other areas where the study of wave phenomena is essential.
Related Exams
About this Document
|
4.68/5 Rating |
|
Nov 22, 2024 Last updated |
Document Description: Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences for Mathematics 2024 is part of Mathematics for IIT JAM, GATE, CSIR NET, UGC NET preparation.
The notes and questions for Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences have been prepared according to the Mathematics exam syllabus. Information about Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences covers topics
like and Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences Example, for Mathematics 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences.
Introduction of Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences in English is available as part of our Mathematics for IIT JAM, GATE, CSIR NET, UGC NET
for Mathematics & Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences in Hindi for Mathematics for IIT JAM, GATE, CSIR NET, UGC NET course.
Download more important topics related with notes, lectures and mock test series for Mathematics
Exam by signing up for free. Mathematics: Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences | Mathematics for IIT JAM, GATE, CSIR NET, UGC NET
Description
Full syllabus notes, lecture & questions for Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences | Mathematics for IIT JAM, GATE, CSIR NET, UGC NET - Mathematics | Plus excerises question with solution to help you revise complete syllabus for Mathematics for IIT JAM, GATE, CSIR NET, UGC NET | Best notes, free PDF download
Information about Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences
In this doc you can find the meaning of Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences defined & explained in the simplest way possible. Besides explaining types of
Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences theory, EduRev gives you an ample number of questions to practice Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences tests, examples and also practice Mathematics
tests
|
556 videos|198 docs
|
Download as PDF
|
Explore Courses for Mathematics exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
Semester Notes
,Important questions
,GATE
,video lectures
,UGC NET
,UGC NET
,study material
,Previous Year Questions with Solutions
,mock tests for examination
,GATE
,Sample Paper
,Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences | Mathematics for IIT JAM
,CSIR NET
,Summary
,Objective type Questions
,GATE
,ppt
,Free
,Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences | Mathematics for IIT JAM
,MCQs
,UGC NET
,practice quizzes
,Viva Questions
,Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences | Mathematics for IIT JAM
,Extra Questions
,CSIR NET
,shortcuts and tricks
,CSIR NET
,Exam
,past year papers
;
Additional Information about Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences for Mathematics Preparation
Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences Free PDF Download
The Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences is an invaluable resource that delves deep into the core of the Mathematics exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences now and kickstart your journey towards success in the Mathematics exam.
Importance of Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences
The importance of Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences cannot be overstated, especially for Mathematics aspirants.
This document holds the key to success in the Mathematics exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences Notes
Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences Notes on EduRev are your ultimate resource for success.
Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences Mathematics Questions
The "Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences Mathematics Questions" guide is a valuable resource for all aspiring students preparing for the
Mathematics exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences on the App
Students of Mathematics can study Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Method of Separation of Variables for Wave Equation - CSIR-NET Mathematical Sciences is prepared as per the latest Mathematics syllabus.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup