Class 9 Exam > Class 9 Notes > Mathematics (Maths) Class 9 > Mind Map: Heron's Formula
Mind Map: Heron's Formula | Mathematics (Maths) Class 9 PDF Download
The document Mind Map: Heron's Formula | Mathematics (Maths) Class 9 is a part of the Class 9 Course Mathematics (Maths) Class 9.
All you need of Class 9 at this link: Class 9
|
40 videos|471 docs|57 tests
|
FAQs on Mind Map: Heron's Formula - Mathematics (Maths) Class 9
| 1. What is Heron's Formula and how is it used to find the area of a triangle? |  |
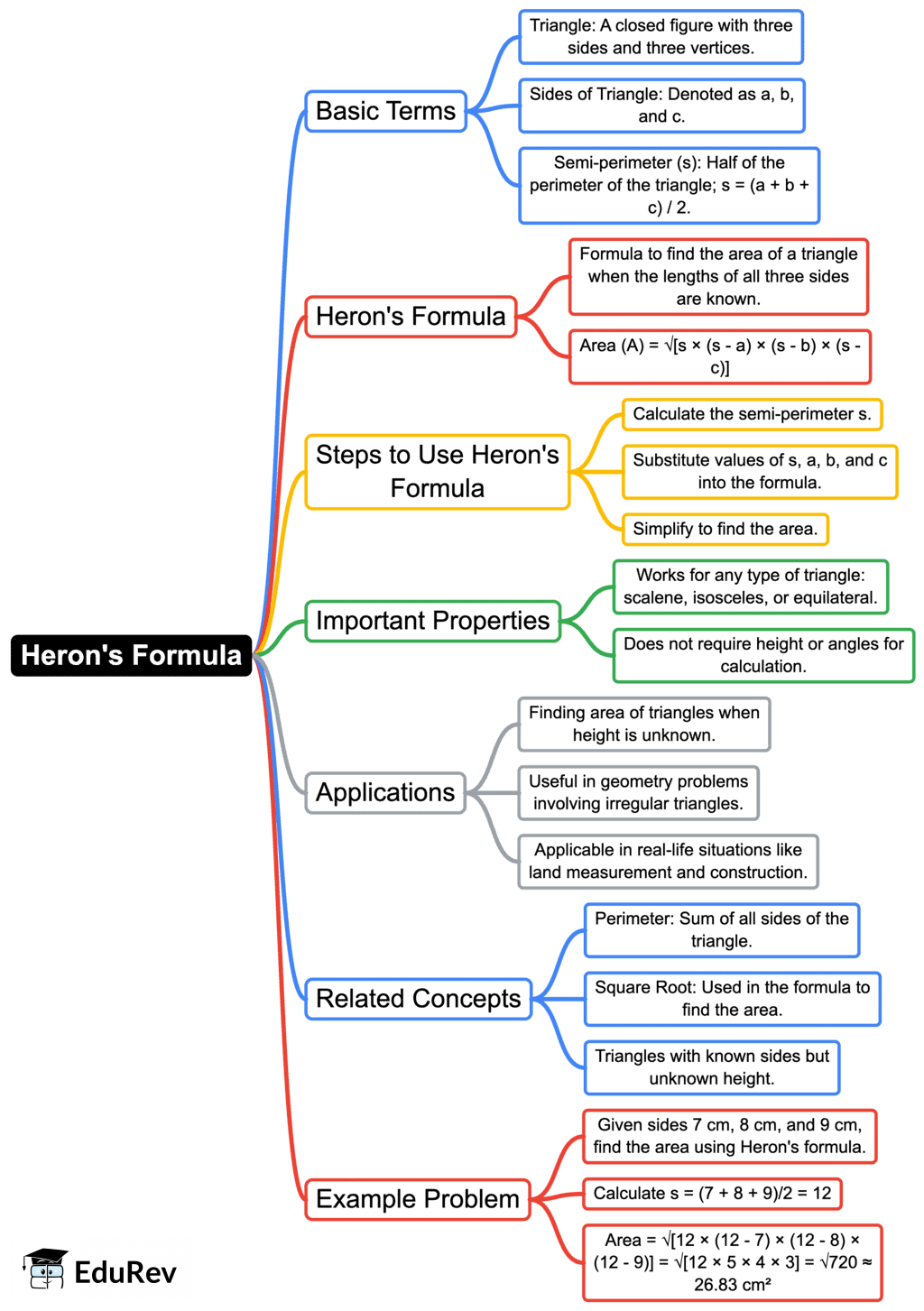
Ans. Heron's Formula is a mathematical formula used to calculate the area of a triangle when the lengths of all three sides are known. The formula states that the area (A) can be found using the semi-perimeter (s) of the triangle. First, calculate the semi-perimeter using s = (a + b + c) / 2, where a, b, and c are the lengths of the sides. Then, the area is given by A = √[s(s - a)(s - b)(s - c)].
| 2. How do you calculate the semi-perimeter in Heron's Formula? |  |
Ans. The semi-perimeter (s) of a triangle is calculated by adding the lengths of all three sides and then dividing by 2. The formula is s = (a + b + c) / 2, where a, b, and c are the lengths of the sides of the triangle.
| 3. Can Heron's Formula be used for triangles with decimal side lengths? |  |
Ans. Yes, Heron's Formula can be used for triangles with decimal side lengths. The formula works for any real numbers as long as they satisfy the triangle inequality, meaning the sum of the lengths of any two sides must be greater than the length of the remaining side.
| 4. What are the steps to apply Heron's Formula in a problem? |  |
Ans. To apply Heron's Formula, follow these steps:
1. Identify the lengths of the three sides of the triangle (a, b, c).
2. Calculate the semi-perimeter using s = (a + b + c) / 2.
3. Substitute the values of s, a, b, and c into the formula A = √[s(s - a)(s - b)(s - c)].
4. Calculate the area (A) using the above formula.
| 5. What are some common mistakes to avoid when using Heron's Formula? |  |
Ans. Common mistakes when using Heron's Formula include:
1. Failing to check if the given side lengths form a valid triangle (triangle inequality).
2. Miscalculating the semi-perimeter due to arithmetic errors.
3. Not correctly substituting the values into the formula.
4. Confusing the area calculation with that of other shapes, leading to incorrect results.
Related Searches
















