Electrical Engineering (EE) Exam > Electrical Engineering (EE) Notes > Digital Electronics > Mind Map: Karnaugh Maps (K-Maps)
Mind Map: Karnaugh Maps (K-Maps) | Digital Electronics - Electrical Engineering (EE) PDF Download
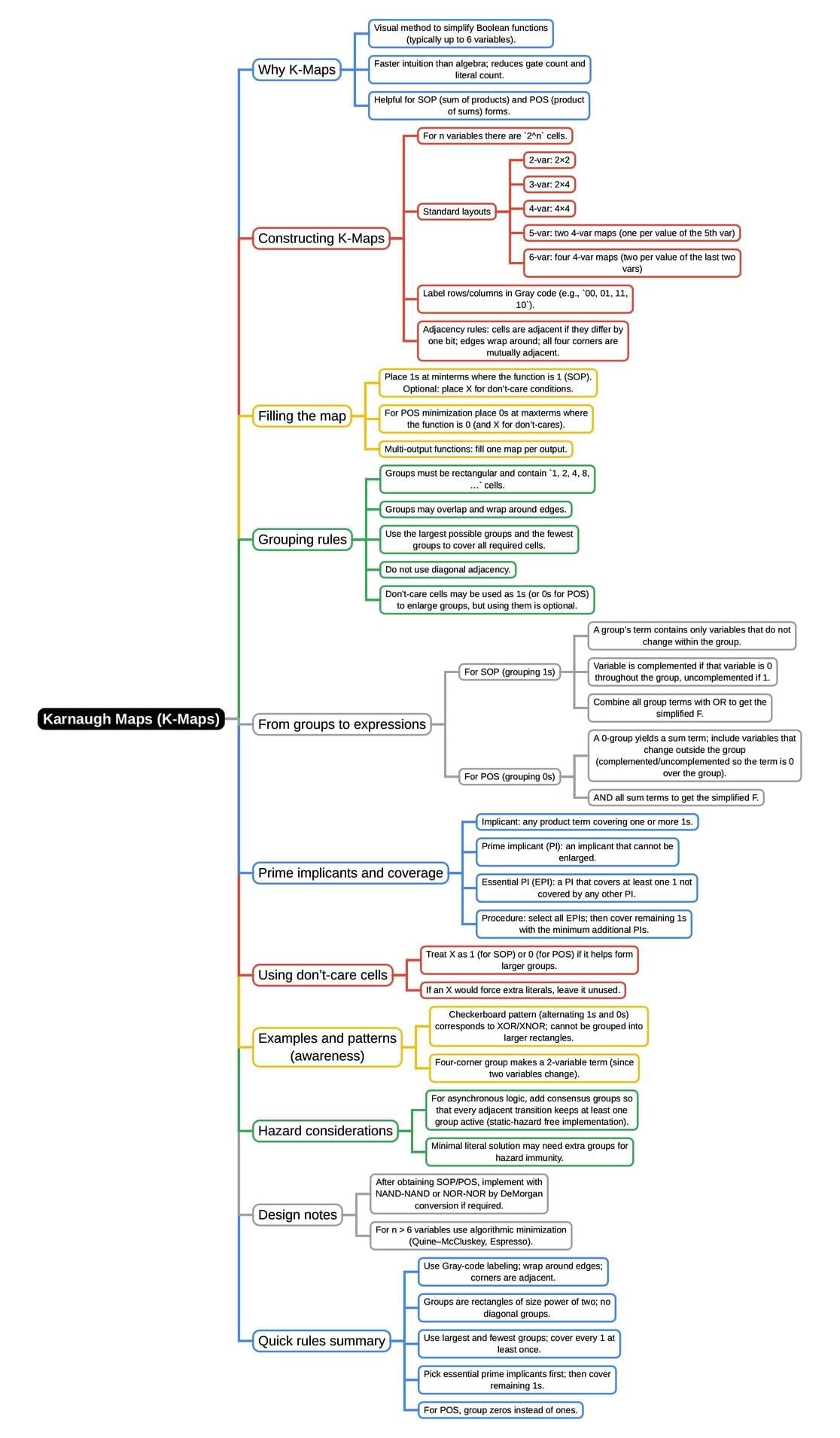
The document Mind Map: Karnaugh Maps (K-Maps) | Digital Electronics - Electrical Engineering (EE) is a part of the Electrical Engineering (EE) Course Digital Electronics.
All you need of Electrical Engineering (EE) at this link: Electrical Engineering (EE)
|
113 videos|91 docs|58 tests
|
FAQs on Mind Map: Karnaugh Maps (K-Maps) - Digital Electronics - Electrical Engineering (EE)
| 1. What is a Karnaugh Map (K-map) and how is it used in simplifying Boolean expressions? |  |
Ans. A Karnaugh Map (K-map) is a graphical representation used to simplify Boolean algebra expressions. It consists of a grid where each cell represents a minterm of the function. K-maps help visualize relationships between variables and identify groups of adjacent cells that can be combined to eliminate variables, thus simplifying the expression. This method is particularly useful for functions with up to six variables, allowing engineers to minimize logic circuits efficiently.
| 2. How do you construct a Karnaugh Map for a given Boolean function? | |
Ans. To construct a K-map for a Boolean function, follow these steps: First, identify the number of variables in the function, which determines the size of the K-map (2ⁿ cells for n variables). Label the rows and columns using Gray code to ensure only one variable changes between adjacent cells. Next, fill in the K-map by placing '1' in cells corresponding to the minterms of the function and '0' elsewhere. Finally, group the '1's in pairs, quads, or octets to simplify the Boolean expression.
| 3. What are the advantages of using Karnaugh Maps over other methods of Boolean simplification? | |
Ans. The advantages of using K-maps include their visual nature, which makes it easier to identify simplifications without complicated calculations. They are particularly effective for functions with a small number of variables, providing a straightforward way to minimize logic expressions. Additionally, K-maps help prevent errors that may occur in algebraic manipulation by allowing designers to see the relationships between variables clearly.
| 4. Can Karnaugh Maps be used for functions with more than six variables? | |
Ans. While K-maps can technically be extended to handle functions with more than six variables, they become impractical due to the exponential increase in grid size and complexity. For functions with more than six variables, other methods such as the Quine-McCluskey algorithm or computer-aided design tools are typically preferred, as these can handle larger datasets more efficiently without the cumbersome nature of large K-maps.
| 5. What is the significance of grouping in Karnaugh Maps, and what are the rules for grouping cells? | |
Ans. Grouping in K-maps is crucial for simplifying Boolean expressions. The significance lies in the ability to combine adjacent cells containing '1's, which leads to the elimination of variables and reduction of the expression. The rules for grouping include: groups must contain 1, 2, 4, 8, etc. cells (powers of 2), groups can wrap around the edges of the map, and each '1' must be included in at least one group. Overlapping groups can also be formed to achieve further simplification.
About this Document
Oct 10, 2025
Last updated
Related Exams
Document Description: Mind Map: Karnaugh Maps (K-Maps) for Electrical Engineering (EE) 2025 is part of Digital Electronics preparation.
The notes and questions for Mind Map: Karnaugh Maps (K-Maps) have been prepared according to the Electrical Engineering (EE) exam syllabus. Information about Mind Map: Karnaugh Maps (K-Maps) covers topics
like and Mind Map: Karnaugh Maps (K-Maps) Example, for Electrical Engineering (EE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Mind Map: Karnaugh Maps (K-Maps).
Introduction of Mind Map: Karnaugh Maps (K-Maps) in English is available as part of our Digital Electronics
for Electrical Engineering (EE) & Mind Map: Karnaugh Maps (K-Maps) in Hindi for Digital Electronics course.
Download more important topics related with notes, lectures and mock test series for Electrical Engineering (EE)
Exam by signing up for free. Electrical Engineering (EE): Mind Map: Karnaugh Maps (K-Maps) | Digital Electronics - Electrical Engineering (EE)
Description
Full syllabus notes, lecture & questions for Mind Map: Karnaugh Maps (K-Maps) | Digital Electronics - Electrical Engineering (EE) - Electrical Engineering (EE) | Plus excerises question with solution to help you revise complete syllabus for Digital Electronics | Best notes, free PDF download
Information about Mind Map: Karnaugh Maps (K-Maps)
In this doc you can find the meaning of Mind Map: Karnaugh Maps (K-Maps) defined & explained in the simplest way possible. Besides explaining types of
Mind Map: Karnaugh Maps (K-Maps) theory, EduRev gives you an ample number of questions to practice Mind Map: Karnaugh Maps (K-Maps) tests, examples and also practice Electrical Engineering (EE)
tests
Related Searches
Important questions
,Mind Map: Karnaugh Maps (K-Maps) | Digital Electronics - Electrical Engineering (EE)
,ppt
,video lectures
,Sample Paper
,Mind Map: Karnaugh Maps (K-Maps) | Digital Electronics - Electrical Engineering (EE)
,practice quizzes
,past year papers
,MCQs
,Semester Notes
,Viva Questions
,Objective type Questions
,shortcuts and tricks
,mock tests for examination
,Previous Year Questions with Solutions
,study material
,Extra Questions
,Free
,Exam
,Mind Map: Karnaugh Maps (K-Maps) | Digital Electronics - Electrical Engineering (EE)
,Summary
;
Additional Information about Mind Map: Karnaugh Maps (K-Maps) for Electrical Engineering (EE) Preparation
Mind Map: Karnaugh Maps (K-Maps) Free PDF Download
The Mind Map: Karnaugh Maps (K-Maps) is an invaluable resource that delves deep into the core of the Electrical Engineering (EE) exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Mind Map: Karnaugh Maps (K-Maps) now and kickstart your journey towards success in the Electrical Engineering (EE) exam.
Importance of Mind Map: Karnaugh Maps (K-Maps)
The importance of Mind Map: Karnaugh Maps (K-Maps) cannot be overstated, especially for Electrical Engineering (EE) aspirants.
This document holds the key to success in the Electrical Engineering (EE) exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Mind Map: Karnaugh Maps (K-Maps) Notes
Mind Map: Karnaugh Maps (K-Maps) Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Mind Map: Karnaugh Maps (K-Maps).
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Mind Map: Karnaugh Maps (K-Maps) Notes on EduRev are your ultimate resource for success.
Mind Map: Karnaugh Maps (K-Maps) Electrical Engineering (EE) Questions
The "Mind Map: Karnaugh Maps (K-Maps) Electrical Engineering (EE) Questions" guide is a valuable resource for all aspiring students preparing for the
Electrical Engineering (EE) exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Mind Map: Karnaugh Maps (K-Maps) on the App
Students of Electrical Engineering (EE) can study Mind Map: Karnaugh Maps (K-Maps) alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Mind Map: Karnaugh Maps (K-Maps),
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Mind Map: Karnaugh Maps (K-Maps) is prepared as per the latest Electrical Engineering (EE) syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup