Class 9 Exam > Class 9 Notes > Mathematics (Maths) Class 9 > Mind Map: Polynomials
Mind Map: Polynomials | Mathematics (Maths) Class 9 PDF Download
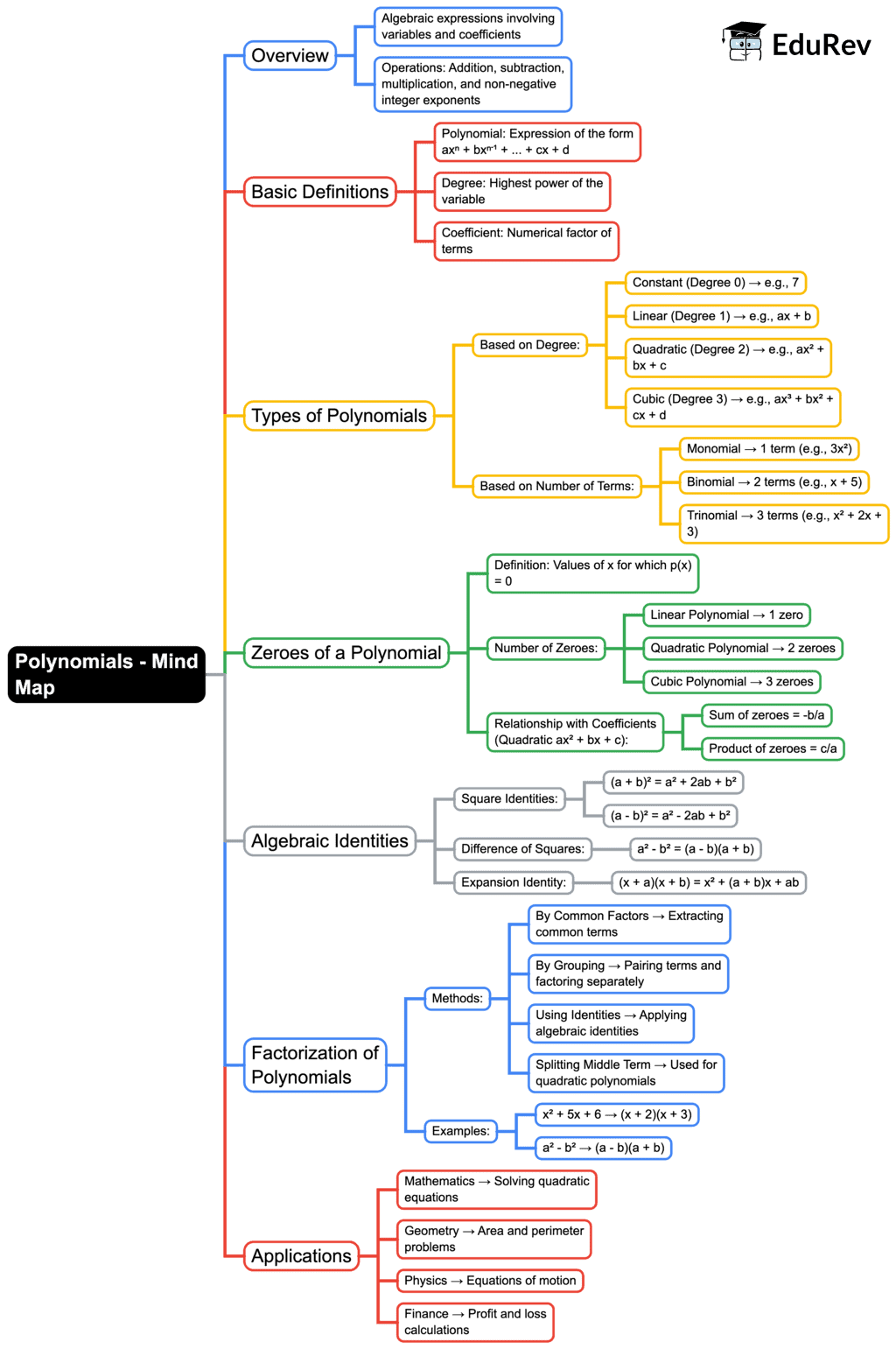
The document Mind Map: Polynomials | Mathematics (Maths) Class 9 is a part of the Class 9 Course Mathematics (Maths) Class 9.
All you need of Class 9 at this link: Class 9
|
40 videos|560 docs|57 tests
|
FAQs on Mind Map: Polynomials - Mathematics (Maths) Class 9
| 1. What are polynomials and how are they classified ? |  |
Ans. Polynomials are algebraic expressions that consist of variables raised to non-negative integer powers and coefficients. They can be classified based on the number of terms:
1. Monomial: An expression with one term (e.g., 3x²).
2. Binomial: An expression with two terms (e.g., 2x² + 3x).
3. Trinomial: An expression with three terms (e.g., x² + 2x + 1).
Additionally, they can be classified by their degree, which is the highest power of the variable (e.g., a polynomial of degree 3 has the form ax³ + bx² + cx + d).
| 2. How do you add and subtract polynomials ? | |
Ans. To add or subtract polynomials, you combine like terms. Like terms are those that have the same variable raised to the same power. For example, to add (3x² + 4x) and (2x² + 5), you combine the coefficients of like terms:
(3x² + 2x²) + 4x + 5 = 5x² + 4x + 5.
For subtraction, you subtract the coefficients of like terms:
(3x² + 4x) - (2x² + 5) = (3x² - 2x²) + 4x - 5 = x² + 4x - 5.
| 3. What is the significance of the degree of a polynomial ? | |
Ans. The degree of a polynomial is significant because it determines the polynomial's behavior and characteristics. The degree indicates the maximum number of roots (solutions) the polynomial can have. For instance, a polynomial of degree n can have up to n real roots. Additionally, the degree influences the graph of the polynomial, such as the number of turns it may have and its end behavior. Higher degree polynomials can exhibit more complex shapes compared to lower degree ones.
| 4. How can polynomials be factored ? | |
Ans. Polynomials can be factored by finding their roots or using various factoring techniques. Common methods include:
1. Factoring out the greatest common factor (GCF).
2. Factoring by grouping, where terms are grouped to find common factors.
3. Using special identities, such as difference of squares (a² - b² = (a + b)(a - b)) and perfect square trinomials.
4. Applying the quadratic formula for polynomials of degree 2 to find roots, then expressing the polynomial as a product of its linear factors.
| 5. What are some real-life applications of polynomials ? | |
Ans. Polynomials have various real-life applications, including:
1. Physics: Modeling motion and forces, where equations can be represented as polynomials.
2. Engineering: Designing structures and systems, as many design equations are polynomial functions.
3. Economics: Calculating profit and loss scenarios using polynomial equations to predict outcomes based on different variables.
4. Computer science: Algorithms for data processing often use polynomial time complexity for efficiency.
5. Biology: Modeling population growth and decay, where polynomial equations can represent growth rates.
About this Document
4.88/5
Rating
Sep 04, 2025
Last updated
Related Exams
Document Description: Mind Map: Polynomials for Class 9 2025 is part of Mathematics (Maths) Class 9 preparation.
The notes and questions for Mind Map: Polynomials have been prepared according to the Class 9 exam syllabus. Information about Mind Map: Polynomials covers topics
like and Mind Map: Polynomials Example, for Class 9 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Mind Map: Polynomials.
Introduction of Mind Map: Polynomials in English is available as part of our Mathematics (Maths) Class 9
for Class 9 & Mind Map: Polynomials in Hindi for Mathematics (Maths) Class 9 course.
Download more important topics related with notes, lectures and mock test series for Class 9
Exam by signing up for free. Class 9: Mind Map: Polynomials | Mathematics (Maths) Class 9
Description
Full syllabus notes, lecture & questions for Mind Map: Polynomials | Mathematics (Maths) Class 9 - Class 9 | Plus excerises question with solution to help you revise complete syllabus for Mathematics (Maths) Class 9 | Best notes, free PDF download
Information about Mind Map: Polynomials
In this doc you can find the meaning of Mind Map: Polynomials defined & explained in the simplest way possible. Besides explaining types of
Mind Map: Polynomials theory, EduRev gives you an ample number of questions to practice Mind Map: Polynomials tests, examples and also practice Class 9
tests
Related Searches
Mind Map: Polynomials | Mathematics (Maths) Class 9
,shortcuts and tricks
,Semester Notes
,video lectures
,mock tests for examination
,Viva Questions
,past year papers
,Important questions
,Free
,Summary
,Objective type Questions
,MCQs
,ppt
,Mind Map: Polynomials | Mathematics (Maths) Class 9
,Mind Map: Polynomials | Mathematics (Maths) Class 9
,Extra Questions
,Sample Paper
,Previous Year Questions with Solutions
,Exam
,practice quizzes
,study material
;
Additional Information about Mind Map: Polynomials for Class 9 Preparation
Mind Map: Polynomials Free PDF Download
The Mind Map: Polynomials is an invaluable resource that delves deep into the core of the Class 9 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Mind Map: Polynomials now and kickstart your journey towards success in the Class 9 exam.
Importance of Mind Map: Polynomials
The importance of Mind Map: Polynomials cannot be overstated, especially for Class 9 aspirants.
This document holds the key to success in the Class 9 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Mind Map: Polynomials Notes
Mind Map: Polynomials Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Mind Map: Polynomials.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Mind Map: Polynomials Notes on EduRev are your ultimate resource for success.
Mind Map: Polynomials Class 9 Questions
The "Mind Map: Polynomials Class 9 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 9 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Mind Map: Polynomials on the App
Students of Class 9 can study Mind Map: Polynomials alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Mind Map: Polynomials,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Mind Map: Polynomials is prepared as per the latest Class 9 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup