Class 8 Exam > Class 8 Notes > Mathematics Class 8- New NCERT (Ganita Prakash) > Mind Map: Quadrilaterals
Mind Map: Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash) PDF Download
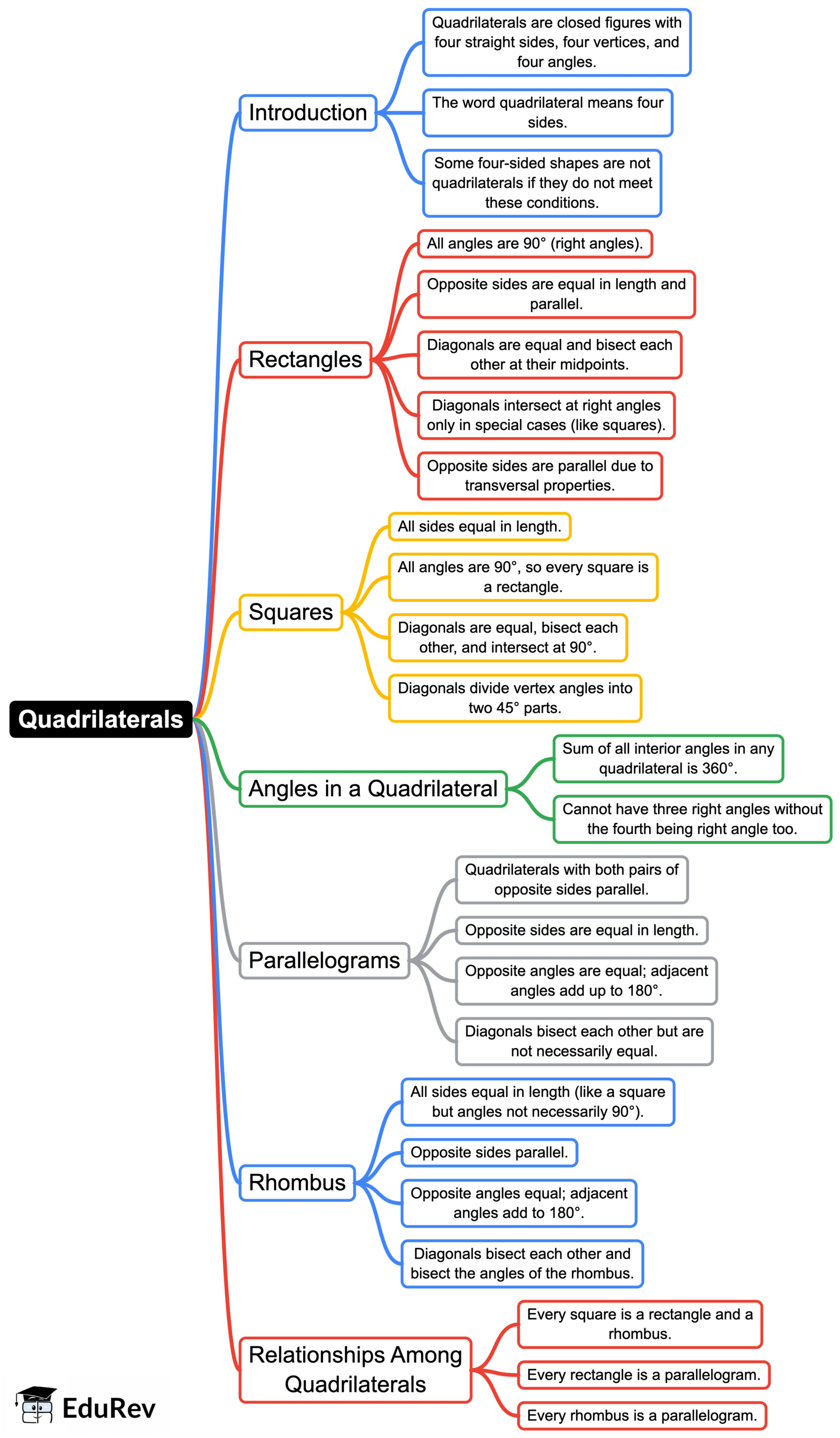
The document Mind Map: Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash) is a part of the Class 8 Course Mathematics Class 8- New NCERT (Ganita Prakash).
All you need of Class 8 at this link: Class 8
|
22 videos|133 docs|11 tests
|
FAQs on Mind Map: Quadrilaterals - Mathematics Class 8- New NCERT (Ganita Prakash)
| 1. What are the different types of quadrilaterals and how are they categorized? |  |
Ans. Quadrilaterals are categorized based on their properties such as sides and angles. The main types include:
1. Square: All sides are equal, and all angles are 90 degrees.
2. Rectangle: Opposite sides are equal, and all angles are 90 degrees.
3. Rhombus: All sides are equal, but angles are not necessarily 90 degrees.
4. Parallelogram: Opposite sides are equal and parallel, and opposite angles are equal.
5. Trapezium (or trapezoid): Only one pair of opposite sides is parallel.
6. Kite: Two pairs of adjacent sides are equal.
| 2. What is the significance of the sum of the interior angles of a quadrilateral? | |
Ans. The sum of the interior angles of a quadrilateral is always 360 degrees. This property is significant because it helps in solving various geometric problems involving quadrilaterals, such as finding unknown angles when some angles are given. This sum is derived from the fact that a quadrilateral can be divided into two triangles, each having a sum of angles equal to 180 degrees.
| 3. How can we determine the area of different types of quadrilaterals? | |
Ans. The area of quadrilaterals can be calculated using different formulas based on their type:
1. Square: Area = side × side (s²).
2. Rectangle: Area = length × width (l × w).
3. Parallelogram: Area = base × height (b × h).
4. Trapezium: Area = (1/2) × (sum of parallel sides) × height.
5. Rhombus: Area = (diagonal₁ × diagonal₂) / 2.
Understanding these formulas is essential for solving problems related to quadrilaterals in geometry.
| 4. What are the properties of a parallelogram that distinguish it from other quadrilaterals? | |
Ans. Parallelograms have several unique properties that set them apart from other quadrilaterals:
1. Opposite sides are equal in length and parallel.
2. Opposite angles are equal.
3. The diagonals bisect each other at their midpoints.
4. The sum of the interior angles is 360 degrees.
These properties are critical for identifying and working with parallelograms in various geometric contexts.
| 5. How do the properties of a kite differ from those of other quadrilaterals? | |
Ans. Kites have distinct properties that differentiate them from other quadrilaterals:
1. Two pairs of adjacent sides are equal in length.
2. One pair of opposite angles (the angles between the unequal sides) are equal.
3. The diagonals intersect at right angles, and one diagonal bisects the other.
These unique characteristics are important for recognizing kites in geometric problems and understanding their behavior in various scenarios.
About this Document
4.92/5
Rating
Oct 02, 2025
Last updated
Related Exams
Document Description: Mind Map: Quadrilaterals for Class 8 2025 is part of Mathematics Class 8- New NCERT (Ganita Prakash) preparation.
The notes and questions for Mind Map: Quadrilaterals have been prepared according to the Class 8 exam syllabus. Information about Mind Map: Quadrilaterals covers topics
like and Mind Map: Quadrilaterals Example, for Class 8 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Mind Map: Quadrilaterals.
Introduction of Mind Map: Quadrilaterals in English is available as part of our Mathematics Class 8- New NCERT (Ganita Prakash)
for Class 8 & Mind Map: Quadrilaterals in Hindi for Mathematics Class 8- New NCERT (Ganita Prakash) course.
Download more important topics related with notes, lectures and mock test series for Class 8
Exam by signing up for free. Class 8: Mind Map: Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash)
Description
Full syllabus notes, lecture & questions for Mind Map: Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash) - Class 8 | Plus excerises question with solution to help you revise complete syllabus for Mathematics Class 8- New NCERT (Ganita Prakash) | Best notes, free PDF download
Information about Mind Map: Quadrilaterals
In this doc you can find the meaning of Mind Map: Quadrilaterals defined & explained in the simplest way possible. Besides explaining types of
Mind Map: Quadrilaterals theory, EduRev gives you an ample number of questions to practice Mind Map: Quadrilaterals tests, examples and also practice Class 8
tests
Related Searches
Viva Questions
,Important questions
,Summary
,Mind Map: Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash)
,Exam
,mock tests for examination
,study material
,shortcuts and tricks
,Mind Map: Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash)
,practice quizzes
,Mind Map: Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash)
,past year papers
,ppt
,Objective type Questions
,Semester Notes
,Sample Paper
,MCQs
,video lectures
,Extra Questions
,Free
,Previous Year Questions with Solutions
;
Additional Information about Mind Map: Quadrilaterals for Class 8 Preparation
Mind Map: Quadrilaterals Free PDF Download
The Mind Map: Quadrilaterals is an invaluable resource that delves deep into the core of the Class 8 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Mind Map: Quadrilaterals now and kickstart your journey towards success in the Class 8 exam.
Importance of Mind Map: Quadrilaterals
The importance of Mind Map: Quadrilaterals cannot be overstated, especially for Class 8 aspirants.
This document holds the key to success in the Class 8 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Mind Map: Quadrilaterals Notes
Mind Map: Quadrilaterals Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Mind Map: Quadrilaterals.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Mind Map: Quadrilaterals Notes on EduRev are your ultimate resource for success.
Mind Map: Quadrilaterals Class 8 Questions
The "Mind Map: Quadrilaterals Class 8 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 8 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Mind Map: Quadrilaterals on the App
Students of Class 8 can study Mind Map: Quadrilaterals alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Mind Map: Quadrilaterals,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Mind Map: Quadrilaterals is prepared as per the latest Class 8 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup