Mechanical Engineering Exam > Mechanical Engineering Notes > General Aptitude for GATE > Mind Map: Ratio & Proportion
Mind Map: Ratio & Proportion | General Aptitude for GATE - Mechanical Engineering PDF Download
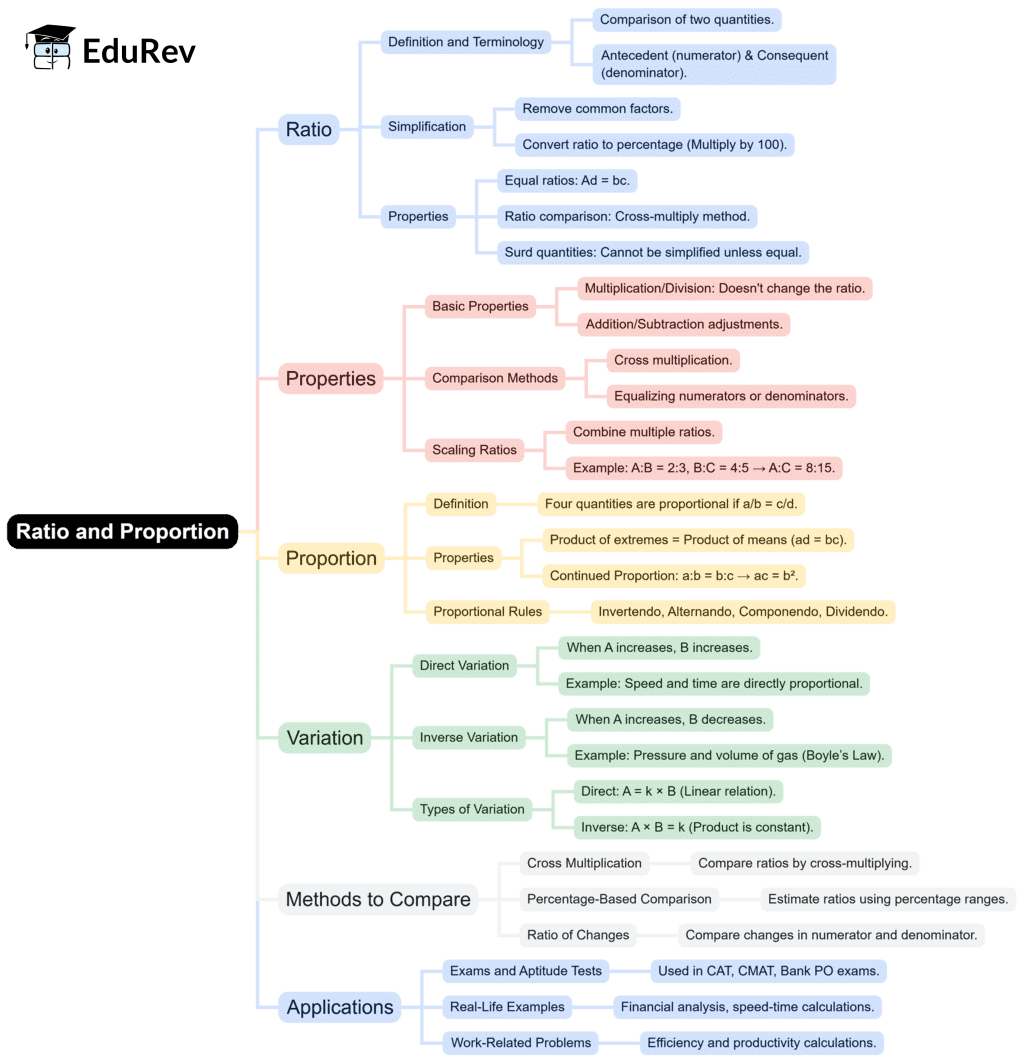
The document Mind Map: Ratio & Proportion | General Aptitude for GATE - Mechanical Engineering is a part of the Mechanical Engineering Course General Aptitude for GATE.
All you need of Mechanical Engineering at this link: Mechanical Engineering
|
193 videos|169 docs|152 tests
|
FAQs on Mind Map: Ratio & Proportion - General Aptitude for GATE - Mechanical Engineering
| 1. What is the difference between ratio and proportion? |  |
Ans. A ratio is a comparison between two quantities, showing how many times one value contains or is contained within the other. For example, if there are 2 apples and 3 oranges, the ratio of apples to oranges is 2:3. On the other hand, proportion refers to the equality of two ratios. For instance, if the ratio of apples to oranges is the same as the ratio of pears to bananas, we can say that these ratios are in proportion.
| 2. How do you solve problems involving ratios and proportions? |  |
Ans. To solve problems involving ratios and proportions, first, express the quantities in the same form. If you have a proportion like a/b = c/d, you can cross-multiply to find the unknown value. This means you multiply a by d and b by c, setting the two products equal. From there, you can solve for the unknown variable by isolating it on one side of the equation.
| 3. Can ratios be simplified like fractions? |  |
Ans. Yes, ratios can be simplified in the same way as fractions. To simplify a ratio, divide both terms by their greatest common divisor (GCD). For example, the ratio 8:12 can be simplified by dividing both 8 and 12 by their GCD, which is 4, resulting in a simplified ratio of 2:3.
| 4. What are some real-life applications of ratio and proportion? |  |
Ans. Ratios and proportions have numerous real-life applications, including cooking (adjusting ingredient quantities), finance (calculating interest rates), and construction (scaling measurements). They are also used in determining speed, density, and in various fields, such as science, to compare different quantities.
| 5. How can I convert a ratio to a percentage? |  |
Ans. To convert a ratio to a percentage, first, express the ratio as a fraction. For example, for the ratio 3:4, you can write it as 3/4. Then, multiply the fraction by 100 to convert it into a percentage. So, 3/4 × 100 = 75%. Therefore, the ratio 3:4 is equivalent to 75%.
Related Searches
















