CAT Exam > CAT Notes > Logical Reasoning (LR) and Data Interpretation (DI) > Mindmap: Venn Diagrams & Set Theory
Mindmap: Venn Diagrams & Set Theory | Logical Reasoning (LR) and Data Interpretation (DI) - CAT PDF Download
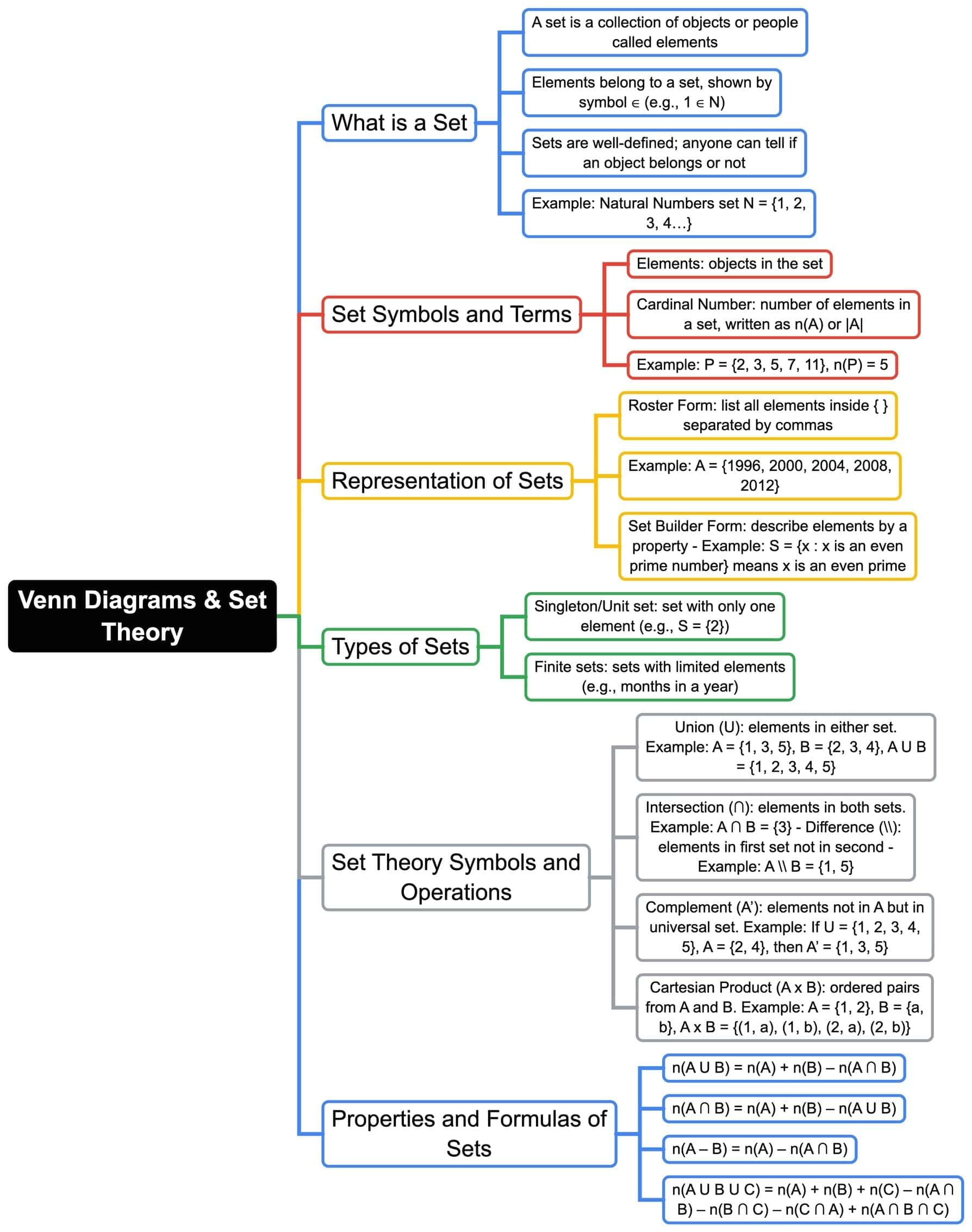
The document Mindmap: Venn Diagrams & Set Theory | Logical Reasoning (LR) and Data Interpretation (DI) - CAT is a part of the CAT Course Logical Reasoning (LR) and Data Interpretation (DI).
All you need of CAT at this link: CAT
|
87 videos|172 docs|99 tests
|
FAQs on Mindmap: Venn Diagrams & Set Theory - Logical Reasoning (LR) and Data Interpretation (DI) - CAT
| 1. What is the basic concept of set theory and how does it relate to Venn diagrams? |  |
Ans. Set theory is a branch of mathematical logic that studies collections of objects, known as sets. It provides the foundational language for mathematics and allows for the exploration of relationships between different sets. Venn diagrams are graphical representations of sets and their relationships, often used to illustrate intersections, unions, and differences between sets. They visually depict how sets overlap and interact, making complex relationships easier to understand.
| 2. How do you determine the union and intersection of two sets using Venn diagrams? | |
Ans. The union of two sets, denoted as A ∪ B, includes all elements that are in either set A or set B or in both. In a Venn diagram, this is represented by shading the areas of both circles. The intersection of two sets, denoted as A ∩ B, includes only the elements that are common to both sets. In a Venn diagram, this is shown by shading the overlapping area of the two circles.
| 3. What are some real-life applications of Venn diagrams and set theory? | |
Ans. Venn diagrams and set theory have numerous applications in real life, including but not limited to: organizing information in databases, analyzing survey data, decision-making processes in business, and understanding relationships in social networks. They are also used in logic and probability, helping to visualize and solve problems involving various sets and their interactions.
| 4. Can you explain the difference between disjoint sets and overlapping sets? | |
Ans. Disjoint sets are sets that have no elements in common; their intersection is empty (A ∩ B = ∅). In a Venn diagram, this is represented by two separate circles that do not touch. Overlapping sets, on the other hand, share some elements, meaning their intersection is not empty (A ∩ B ≠ ∅). In a Venn diagram, this is shown by two circles that intersect, highlighting the shared elements.
| 5. What is the significance of the universal set in set theory? | |
Ans. The universal set, often denoted by U, is the set that contains all possible elements under consideration for a particular discussion or problem. It serves as the context within which all other sets are defined. In set theory, understanding the universal set is crucial because it helps in determining subsets, complements, and relationships among various sets, allowing for a complete analysis of the situation being examined.
About this Document
Sep 22, 2025
Last updated
Related Exams
Document Description: Mindmap: Venn Diagrams & Set Theory for CAT 2025 is part of Logical Reasoning (LR) and Data Interpretation (DI) preparation.
The notes and questions for Mindmap: Venn Diagrams & Set Theory have been prepared according to the CAT exam syllabus. Information about Mindmap: Venn Diagrams & Set Theory covers topics
like and Mindmap: Venn Diagrams & Set Theory Example, for CAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Mindmap: Venn Diagrams & Set Theory.
Introduction of Mindmap: Venn Diagrams & Set Theory in English is available as part of our Logical Reasoning (LR) and Data Interpretation (DI)
for CAT & Mindmap: Venn Diagrams & Set Theory in Hindi for Logical Reasoning (LR) and Data Interpretation (DI) course.
Download more important topics related with notes, lectures and mock test series for CAT
Exam by signing up for free. CAT: Mindmap: Venn Diagrams & Set Theory | Logical Reasoning (LR) and Data Interpretation (DI) - CAT
Description
Full syllabus notes, lecture & questions for Mindmap: Venn Diagrams & Set Theory | Logical Reasoning (LR) and Data Interpretation (DI) - CAT - CAT | Plus excerises question with solution to help you revise complete syllabus for Logical Reasoning (LR) and Data Interpretation (DI) | Best notes, free PDF download
Information about Mindmap: Venn Diagrams & Set Theory
In this doc you can find the meaning of Mindmap: Venn Diagrams & Set Theory defined & explained in the simplest way possible. Besides explaining types of
Mindmap: Venn Diagrams & Set Theory theory, EduRev gives you an ample number of questions to practice Mindmap: Venn Diagrams & Set Theory tests, examples and also practice CAT
tests
Related Searches
shortcuts and tricks
,mock tests for examination
,Mindmap: Venn Diagrams & Set Theory | Logical Reasoning (LR) and Data Interpretation (DI) - CAT
,practice quizzes
,Free
,video lectures
,study material
,Mindmap: Venn Diagrams & Set Theory | Logical Reasoning (LR) and Data Interpretation (DI) - CAT
,MCQs
,ppt
,Important questions
,Mindmap: Venn Diagrams & Set Theory | Logical Reasoning (LR) and Data Interpretation (DI) - CAT
,past year papers
,Viva Questions
,Previous Year Questions with Solutions
,Summary
,Exam
,Extra Questions
,Sample Paper
,Objective type Questions
,Semester Notes
;
Additional Information about Mindmap: Venn Diagrams & Set Theory for CAT Preparation
Mindmap: Venn Diagrams & Set Theory Free PDF Download
The Mindmap: Venn Diagrams & Set Theory is an invaluable resource that delves deep into the core of the CAT exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Mindmap: Venn Diagrams & Set Theory now and kickstart your journey towards success in the CAT exam.
Importance of Mindmap: Venn Diagrams & Set Theory
The importance of Mindmap: Venn Diagrams & Set Theory cannot be overstated, especially for CAT aspirants.
This document holds the key to success in the CAT exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Mindmap: Venn Diagrams & Set Theory Notes
Mindmap: Venn Diagrams & Set Theory Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Mindmap: Venn Diagrams & Set Theory.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Mindmap: Venn Diagrams & Set Theory Notes on EduRev are your ultimate resource for success.
Mindmap: Venn Diagrams & Set Theory CAT Questions
The "Mindmap: Venn Diagrams & Set Theory CAT Questions" guide is a valuable resource for all aspiring students preparing for the
CAT exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Mindmap: Venn Diagrams & Set Theory on the App
Students of CAT can study Mindmap: Venn Diagrams & Set Theory alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Mindmap: Venn Diagrams & Set Theory,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Mindmap: Venn Diagrams & Set Theory is prepared as per the latest CAT syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily