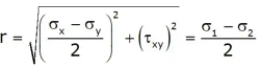Mohr's Circle For Plane Stress & Plane Strain | Strength of Materials (SOM) - Mechanical Engineering PDF Download
Mohr’s circle is the locus of points representing the magnitude of normal and shear stress at the various plane in a given stress element. Graphically, a variation of normal stress and shear stress are studied with the help of Mohr's circle.
σ1 and σ2 are Principal Stresses, then normal and shear stress on lane which is inclined at angle ‘θ’ from major principal plane, then
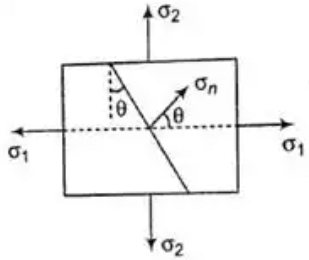 Different Stress Diagram
Different Stress Diagram
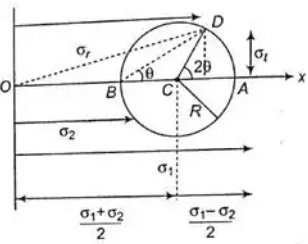 Mohr's circle for plane Stress and StrainNormal Stress
Mohr's circle for plane Stress and StrainNormal Stress
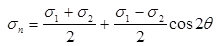
Shear Stress
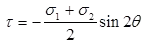
General State of Stress at an Element
If σx and σy are normal stress on vertical and horizontal plane respectively and this plane is accompanied by shear stress then normal stress and shear stress on the plane, which is inclined at an angle θ from the plane of
 then,
then,
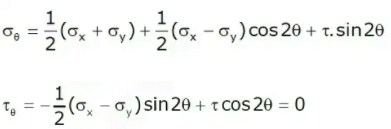
Let σx, σy be two normal stresses(both tensile) and τxy be shear stress then:
Maximum and Minimum Principal Stresses are:
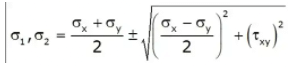
The radius of Mohr’s circle:
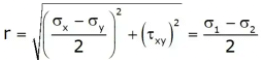
Strength of Materials
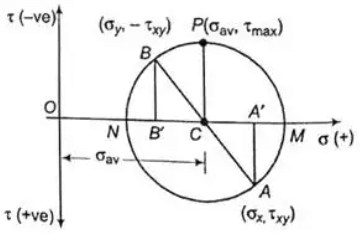 Mohr's circle for plane stressed
Mohr's circle for plane stressed
Observations from Mohr's Circle
The following are the observations of Mohr's circle as:
- At point M on circle σn is maximum and shear stress is zero.
∴ Maximum principal stress ≡ coordinate of M - At point N on circle, σn is minimum and shear stress τ is zero.
∴ minimum principal stress ≡ coordinate of N - At point P on Circle τ is maximum.
Maximum shear stress ≡ ordinate of P(i.e. radius of circle) - Also, normal stress on the plane of maximum shear stress:
σn = abscissa of P Where σn ≡ Average stress
Where σn ≡ Average stress - Mohr's circle becomes zero at a point if radius of circle has the following consideration.
- Radius of circle:

- If σx = σy, then radius of Mohr's circle is zero and τxy = 0.
- The sum of normal stresses acting on perpendicular faces of a plane stress elements is constant and independent of the angle θ.
σ1 + σ2 = σ1 + σ2
Strain analysis



Principle Strain 
∈θ + ∈θ + 90º = ∈x + ∈y
Relation between Principle strain and stress
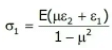
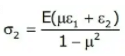
Strain Rosetts
- Rectangular Strain Rosette
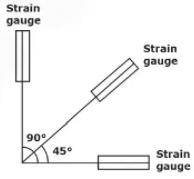 ∈x = ∈0º, ∈y = ∈90º and Ф = 2∈45º - (∈x + ∈y)
∈x = ∈0º, ∈y = ∈90º and Ф = 2∈45º - (∈x + ∈y)
- Equiangular Strain Rosette (delta strain rosette)
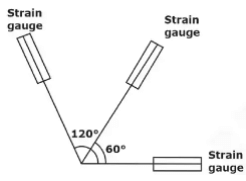 ∈θº = ∈x
∈θº = ∈x
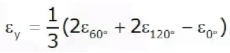
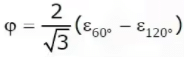
|
37 videos|41 docs|47 tests
|
FAQs on Mohr's Circle For Plane Stress & Plane Strain - Strength of Materials (SOM) - Mechanical Engineering
| 1. What is Mohr's circle and how is it used to analyze plane stress and plane strain? |  |
| 2. What is the difference between plane stress and plane strain? |  |
| 3. How can Mohr's circle be used to determine the principal stresses? |  |
| 4. How is the maximum shear stress determined using Mohr's circle? |  |
| 5. What are the applications of Mohr's circle in mechanical engineering? |  |

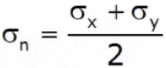 Where σn ≡ Average stress
Where σn ≡ Average stress