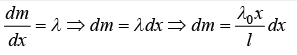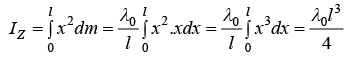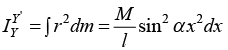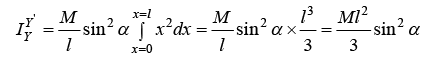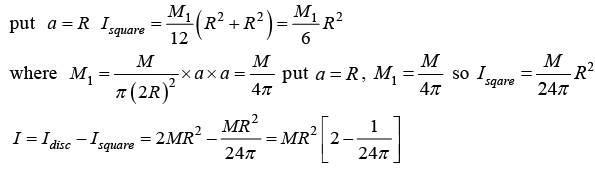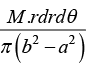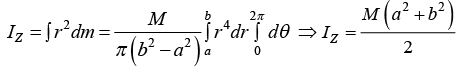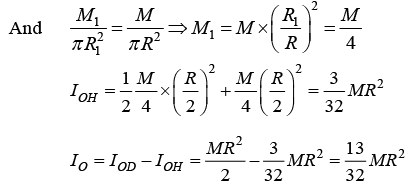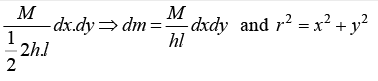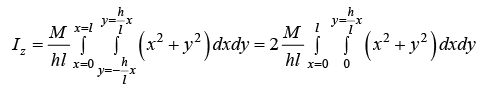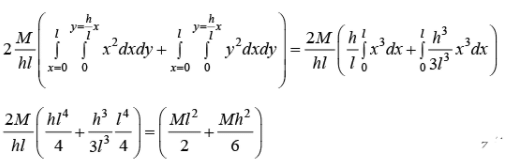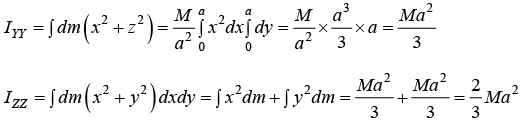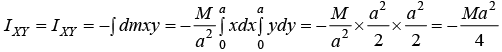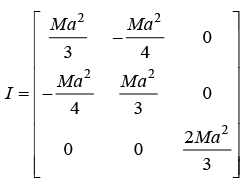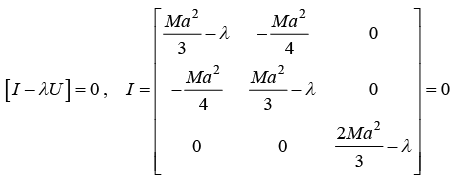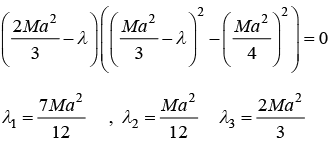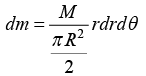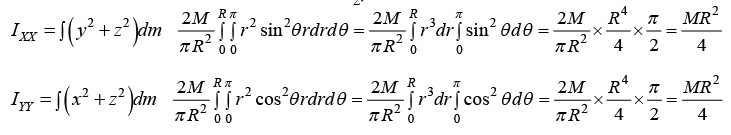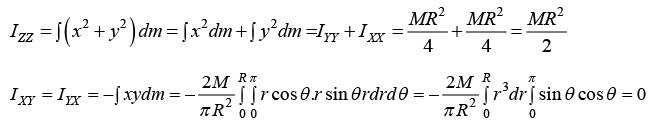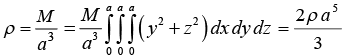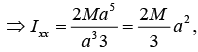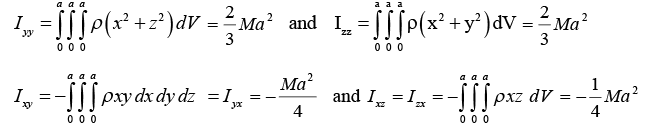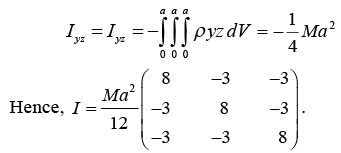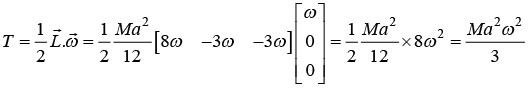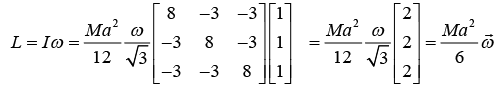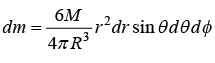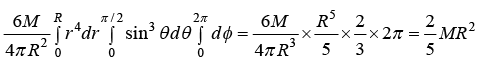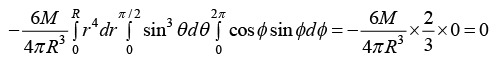Moment of Inertia | Mechanics & General Properties of Matter - Physics PDF Download
Theorems to Calculate Moment of Inertia
Newton’s law of motion for linear motion can be written as 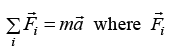 is the external force on particle with mass m the effect of force on mass can be calculated as acceleration
is the external force on particle with mass m the effect of force on mass can be calculated as acceleration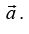 The mass m is also identify of measurement of Inertia. Similarly for the Rotational motion of rigid body about any axis passing through O the equation of motion can be written as torque equation as
The mass m is also identify of measurement of Inertia. Similarly for the Rotational motion of rigid body about any axis passing through O the equation of motion can be written as torque equation as 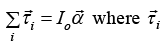 is external torque about axis passing through O and
is external torque about axis passing through O and 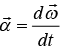 is angular acceleration of Rigid body. IO is Identified as Moment of Inertia of rigid body about axis passing through O.
is angular acceleration of Rigid body. IO is Identified as Moment of Inertia of rigid body about axis passing through O.
So moment of inertia about axis passing through axis O due to small elemental mass dm is given by IO = ∫r2 dm where r is perpendicular distance between elemental mass dm and axis.
For example if elemental mass dm is confined in x,y plane then moment of inertia about Y axis Iy = ∫x2 dm
To solve moment of inertia effectively we use two basic theorem.
1. Theorem of Parallel Axes
Suppose we have to obtain the moment of inertia of a body about a given line AB. Let C be the centre of mass of the body and Axis passing through center of mass is CZ be the line parallel to AB through C. Let I and IC be the moment of inertia of the body about AB and CZ respectively. Then, I = IC + Md2, where d is the perpendicular distance between lines AB and CZ and M is mass of the body.
Let I and IC be the moment of inertia of the body about AB and CZ respectively. Then, I = IC + Md2, where d is the perpendicular distance between lines AB and CZ and M is mass of the body.
2. Theorem of Perpendicular Axes
The perpendicular axis theorem is used only when mass is distributed in plane . if mass is distributed in x - y plane and IX, IY and IZ is principle moment of inertia about x,y, z axis respectively, then according to perpendicular axis theorem
IZ = IX + IY
Moment of Inertia of Particular Cases
A. Uniform Rod
(i) Moment of inertia About an axis through its centre and perpendicular to its length. Let AB be a thin uniform rod, of length l and mass M, free to rotate about an axis YOY' passing through its centre O and perpendicular to its length, as shown in figure. Since the rod is uniform, its mass per unit length is clearly M /l .Considering a small element of the rod, of length dx at a distance x from the axis through O, we have mass of the element dm = (M/l).dx and therefore, its moment of inertia about the axis (YOY') through
Since the rod is uniform, its mass per unit length is clearly M /l .Considering a small element of the rod, of length dx at a distance x from the axis through O, we have mass of the element dm = (M/l).dx and therefore, its moment of inertia about the axis (YOY') through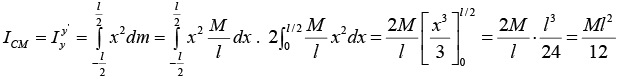
(ii) Moment of inertia about an axis through one end of the rod and perpendicular to its length.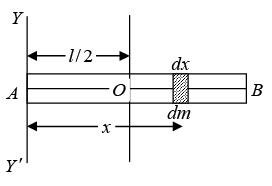
Proceeding as in case (i) above, we obtain the moment of inertia of the rod about the axis, now passing through one end A of the rod, by integrating the expression for the moment of inertia of the element dx of the rod, between the limits x = 0 at A and x = l at B , i.e. ,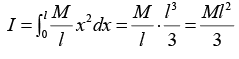
Alternatively, we could obtain the same result by an application of the principle of parallel axes, according to which Moment of inertia of the rod about the axis YAY' = Its moment of inertia about a parallel axis through O + (mass of the rod × square of the distance between the two axes).
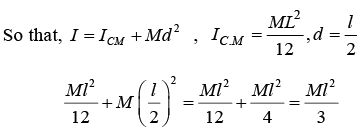
B. Rectangular Lamina (or Bar)
(i) Moment of inertia About an axis through its centre and parallel to one side:
Let AB C D be a rectangular lamina, of length l , breadth b and mass M and let YOY' be the axis through its centre O and parallel to the side AD or BC about which its moment of inertia is to be determined. Consider an element, or a small rectangular strip of the lamina, parallel to, and at a distance x from the axis. The area of this strip or element dA = dx × b . And, since the mass per unit area of the lamina = m/(l xb), we have mass of the strip or element 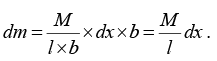
And therefore, M.I. of the element about the axis YOY' 
The moment of inertia (l) of the whole rectangular lamina is then given by twice the integral of the above expression between the limits x = 0 and x = l/2.
(ii) Moment of Inertia about side BC: From principle of parallel axes, I = ICM +md2 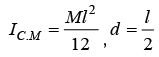
So, moment of inertia about axis which is passing through BC 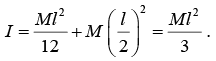
This is again the same case as that of the M.I. of a rod about an axis passing through one of its ends and perpendicular to its length [case I (ii)], for, as pointed out above, if b be small, the rectangular lamina too reduces to a thin rod of length l.
(iii) Moment of inertia about an axis passing through its centre and perpendicular to its plane: This may be easily obtained by an application of the principle of perpendicular axes theorem to
IZ = lX + lY = ml2/12
Similarly, Ix = Mb2/12
Moment of inertia about axis passing through O and perpendicular to plane is
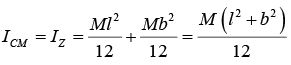
(iv) Moment of inertia of Lamina about an axis passing through the mid-point of one side BC and perpendicular to its plane: In this case the axis passes through the mid-point of side AB or BC , say, and perpendicular to the plane of the lamina, so that it is parallel to the axis through O (the c.m. of the lamina) in case (iii).
In accordance with the principle of parallel axes, therefore, the M. I. of the lamina about this axis is given by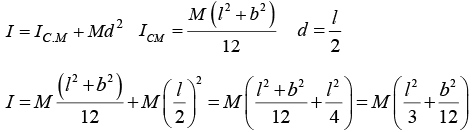
And, if the axis passes through the mid-point of AB or DC , we, similarly have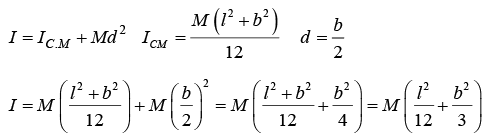
(v) About an axis passing through one of its corners D and perpendicular to its plane: Let the axis passes through the corner D of the lamina. Since it is perpendicular to the plane of the lamina, it is parallel to the axis through its centre of mass O in case (iii). Again, therefore, by the principle of parallel axes, we have moment of inertia of the rectangular lamina about this axis through D given by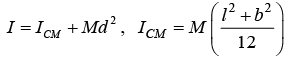
where d is the distance between the two axes. Clearly, d2 = (l /2)2 + (b/2)2 = (l2 + b2)/4 .
So that, 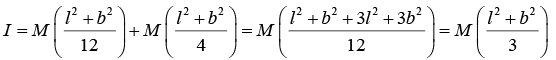
C. Circular Ring
(i) Moment of inertia about an axis through its centre and perpendicular to its plane. Let the radius of the hoop or the thin circular ring be R and its mass M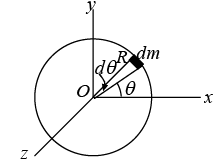
Consider a particle of mass m of the hoop or the ring. Clearly, its M.I. about an axis through the centre O of the hoop or the ring and perpendicular to its plane IZ = ∫dmR2 where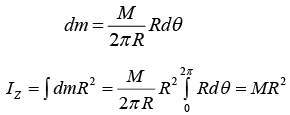
(ii) Moment of inertia about axis, which is passing through its diameter: Obviously, due to symmetry, the M.I. of the hoop or the ring will be the same about one diameter as about another. Thus, if I be its M.I. about the diameter XOX' (Figure), it will also be I about the diameter YOY' perpendicular to XOX'.
By the principle of perpendicular axes theorem, IZ = IX + IY From symmetry IX = IY and IZ = MR2 IX + IX = MR2 or 2IX = MR2 hence, IX = MR2/2.
D. Circular lamina or disc
(i) Moment of inertia about an axis through its centre and perpendicular to its plane:
Let M be the mass of the disc and R , its radius, so that its mass per unit area is equal to M/πR2.
Considering elemental mass of the disc dm, distance r from the axis passing through O and perpendicular to the plane of the disc, we have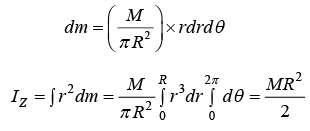
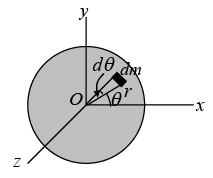
(ii) Moment of inertia about axis, which is passing through its diameter: Here, again, due to symmetry, the M.I. of the disc, about one diameter is the same as about another. So that, if I be the M.I. of the disc about each of the perpendicular diameters XOX' and YOY' , (Figure), By the principle of perpendicular axes theorem, IZ = IX + IY From symmetry IX = IY and IZ = MR2
IX + IX = MR2/2 or.
i.e. 2IX = MR2/2, hence, IX = MR2/4.
E. Solid Cylinder
(i) Moment of inertia of cylinder of radius R and uniform mass M about its own axis of cylindrical symmetry:
Using cylindrical symmetry, x = r cosθ, y =r sin θ and z = z.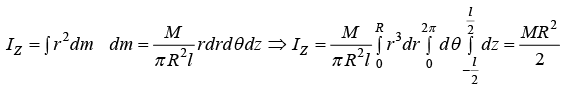
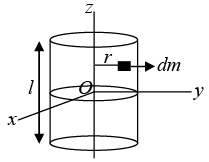
Other method: A solid cylinder is just a thick circular disc or a number of thin circular disc (all of the same radius) piled up one over the other, so that its axis of cylindrical symmetry is the same as the axis passing through the centre of the thick disc (or the pile of thin discs) and perpendicular to its plane.
∴ M.I. of the thick disc (or the pile of thin discs) of the same mass and radius about the axis through its centre and perpendicular to its plane.
or I = MR2/2
(ii) Moment of inertia About the axis through its centre and perpendicular to its axis of cylindrical symmetry: If R be the radius, l the length and M the mass of the solid cylinder, supposed to be uniform and of a homogeneous composition, we have its mass per unit length equal to M/l.
Now, imagining the cylinder to be made up of a number of discs each of radius R , placed adjacent to each other, and considering one such disc of thickness dx and at a distance x from the centre O of the cylinder, (figure), we have
Mass of the disc = (M/I)dx and radius = R
And Δ M.I. of the disc about its diameter AB = M/l dx. R2/4 and its M.I. about the parallel axis YOY' , passing through the centre O of the cylinder and perpendicular to its axis of cylindrical symmetry (or its length), in accordance with the principle of parallel axes,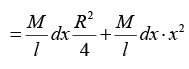
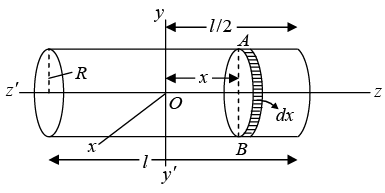
Hence, M.I. of the whole cylinder about this axis, i.e. I = twice the integral of the above expression between the limits x = 0 and x = l/2 ,
i.e., 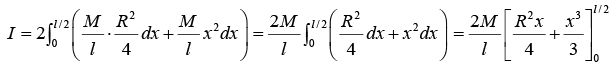
or 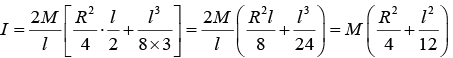
F. Solid cone of mass M and its vertical height h and its base radius R (figure below).
(i) Moment of Inertia about its vertical axis.
Clearly, volume of the cone 1/3 πR2h and if ρ be the density of its material its mass 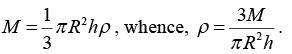 Now, the cone may be imagined to consist of a number of discs of progressively decreasing radii, from R to 0 piled up one over the other.
Now, the cone may be imagined to consist of a number of discs of progressively decreasing radii, from R to 0 piled up one over the other.
Considering one such disc of thickness dx and at a distance x from the vertex A of the cone, we have, Radius of the disc, r = x tanα, where α is the semi-vertical angle of the cone, and therefore its volume = πR2dx = πx2 tan2 αdx and its mass = πx2 tan2 αρdx . Hence, M.I. of the disc about the vertical axis AO of the cone (i.e. an axis passing through its centre and perpendicular to its plane) = mass x (radius)2/2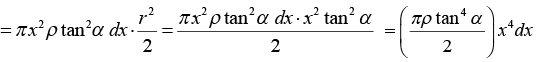
And since, M.I. of the entire cone about its vertical axis AO is given by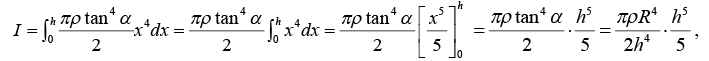
substituting R/h for tanα or, substituting the value of ρ obtained above, we have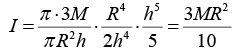
(ii) Moment of inertia about an axis passing through the vertex and parallel to its base: Again, considering the disc at a distance x from the vertex of the cone, we have its M.I. about its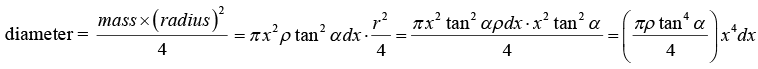
∴ Its M.I. about the parallel axis XX', parallel to its base is given by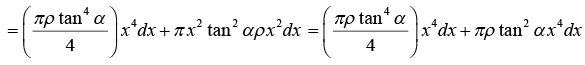
Hence M.I. of the entire cone about the axis XX', parallel to the base is given by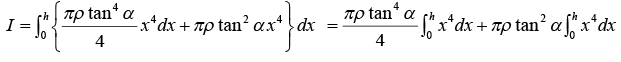
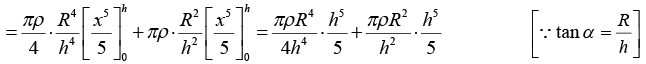
or, substituting the value of ρ, we have M.I. of the cone about the axis XX', i.e.
G. Moment of inertia of a uniform hollow sphere about a diameter
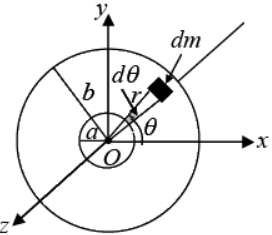
Let M and R be the mass and the radius of the sphere, O its centre and OX the given axis. The mass is spread over the surface of the sphere and the inside is hollow.
Iz = ∫r2 dm where dm = M/4πR2 R2sin θdθd∅ is elemental mass and r = R sinθ , which is perpendicular distance from axis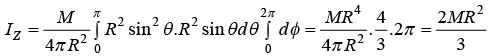
H. Moment of inertia of a uniform solid sphere about a diameter
Let M and R be the mass and the radius of the sphere, O its centre and OX the given axis. The mass is spread over the surface of the sphere and the inside is hollow.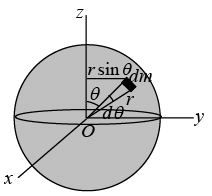
IZ = ∫r2 dm where 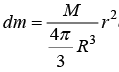 dr sin θdθd∅ is elemental mass and r = R sinθ which is perpendicular distance from axis
dr sin θdθd∅ is elemental mass and r = R sinθ which is perpendicular distance from axis
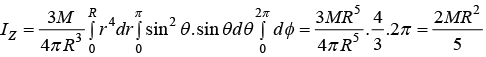
Radius of Gyration: The radius of Gyration K of body about axis is the effective distance from this axis where the whole mass can be assumed to be concentrated so that moment of inertia remain the same.
l = MK2 So K = 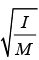
For example radius of gyration of disc about an axis perpendicular to its plane and passing through its center of mass is 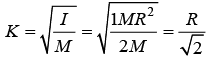
Example 9: If linear mass density of Rod is λ = λ0x/l where l is length of Rod and x is distance measured from origin as shown in figure find the moment of inertia about axis passing through origin.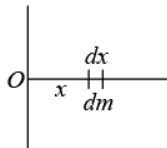
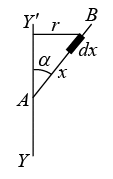
Example 10: Find the moment of inertia of rod AB of mass M and length l about an axis YY' are shown in figure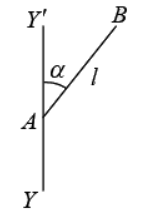
Elemental mass of the rod dm = M/l dx
Perpendicular distance of this elemental mass about YY ' is r = x sin α
Moment of Inertia of this small element of the rod
Example 10: Seven uniform rings, each of mass M and radius R, are inscribed inside a regular hexagon as shown. Find the moment of inertia of this system of seven rings, about an axis passing through the central ring and perpendicular to the plane of the disks.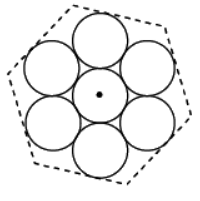
MI of central ring about axis + 6 × MI of surrounding Ring
about axis
MR2 + 6 × (MR2 + M(2R)2) = MR2 + 6× 5MR2 = 31MR2
Example 11: Consider a uniform thin circular disk of radius 2 R and mass M . A concentric square of side R is cut out from the disk (see figure). What is the moment of inertia of the resultant disk about an axis passing through the centre of the disk and perpendicular to it?
Moment of Inertia of about center isM/2(2R)2 = 2MR2
Moment of inertia of square of length a about center is Isquare = M1/12 (α2 + α2)
Example 12: Find the Moment of inertia of Annular Disc of mass M about axis passing through center and perpendicular to plane the inner radius of disc is a and outer radius is b.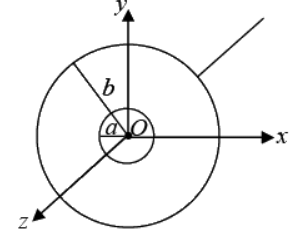
If b and a be the outer and inner radii of the disc having mass M , we have mass per unit area of the disc
The elemental mass dm =
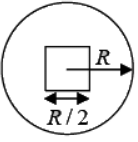
Example 13: Consider a uniform thin circular disk of radius R and mass M . A hole of radius R/2 is cut out from the disk (see figure). What is the moment of inertia of the resultant disk about an axis passing through the centre of the disk O and perpendicular to it?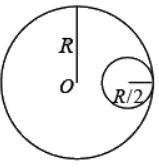
Moment of inertia of disc IOD = MR2/2
Moment of inertia of hole IOH =
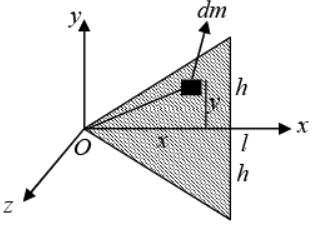
Example 14: Example: Find the moment of Inertia about the axis passing through O and perpendicular to triangular plate of Mass M . Where l and h are given parameter shown in figure.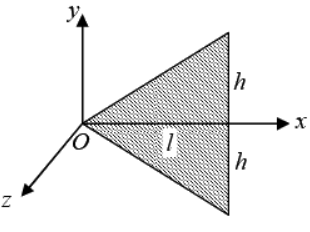
IZ = ∫r2dm where dm =
Moment of Inertia Tensor
Angular Momentum and Inertia Tensor
Let us consider the motion of a rigid body rotating about a fixed point o in the body as shown in figure.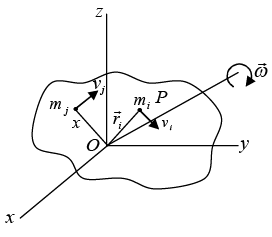 At any instant of time, the body will rotate with velocity ω about that instant through point O. A particle P of the body, having the position vector r1 with respect to O has instantaneous velocity vi relative to O, given by
At any instant of time, the body will rotate with velocity ω about that instant through point O. A particle P of the body, having the position vector r1 with respect to O has instantaneous velocity vi relative to O, given by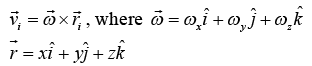
Angular momentum of Point P about the point O is given by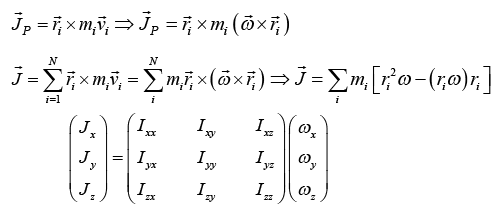
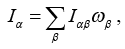 , where Iαβ is inertia tensor
, where Iαβ is inertia tensor
and 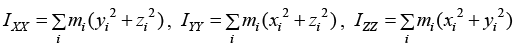 are known as moment of inertia and IXY = IYX
are known as moment of inertia and IXY = IYX 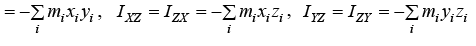 are known as product of inertia.
are known as product of inertia.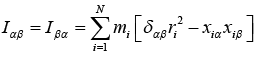
where α = 1, 2, 3 and β = 1, 2, 3 , so one can denote x,y, z by x1,x2, x3 respectively.
For continuous system Iαβ is reduce to
∫dm[δαβxi2 - xiαxiβ where dm is elemental mass.
Principal Moment of Inertia
If one can diagonalized Inertia tensor into diagonal matrix then the diagonal element is known as principal moment of inertia
And x,y, z component of angular momentum reduces to
Jx = Ixxωx + Ixyωy + Ixzωz
Jy = Iyxωx + Iyyωy+ Iyzωz
Jz = Izxωx + Izyωy + Izzωz
The secular equation of characteristic equationby given by [I - λU] = 0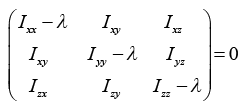
The solution of characteristic equation λ = I1, I2, I3 are three principal moment of inertia. Rotational kinetic energy of a rigid body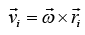
Kinetic energy of particle mi (which is explained in previous topic).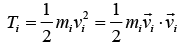
Kinetic energy for entire body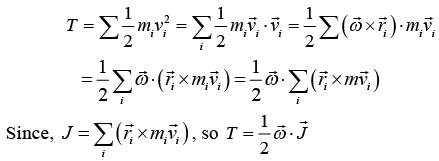
Kinetic energy in a co-ordinate system of principle axis is given by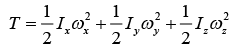
Example 15: (a) Find the moment of inertia of system where square of mass M and area a2 the origin is at one corner as shown in figure.
(b) Find principle moment of inertia
Ixx = ∫dm
IXZ = IZX = -∫dmxz = 0
IYZ = IZY = -∫dmyz = 0
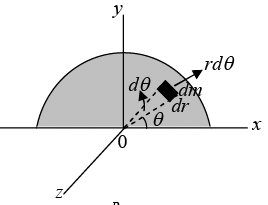
Example 16: Find the moment of inertia tensor of semi circular disc of mass M and radius R where origin is at the center of disc.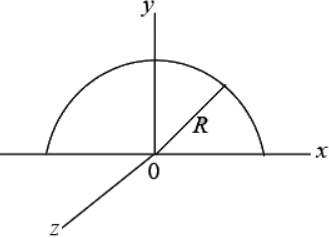
We can solve the problem in circular polar coordinate x = r cosθ, y = r sinθ, z = 0
IXZ = IZX = -∫xzdm = 0 IYZ = IZY = -∫yzdm = 0
The moment of inertia tensor
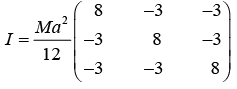
Example 17: Consider a cube of volume a3 and mass M, which is situated such the origin O is at one of the corner, consider cube has uniform density ρ. Then,
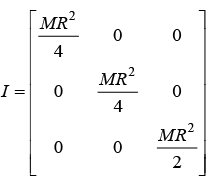
(a) Find the moment of inertia tensor.
(b) Find the principal moment of inertia tensor.
(c) Find the angular momentum and kinetic energy when the axis of rotation is parallel to x [that is, ω = (ω,0,0)]
(d) Find the angular momentum when the axis of rotation is parallel to is along the body diagonal in the direction (1,1,1).
(a) Ixx = ∫ρ(y2 + z2) dv where
Similarly,
(b) Principle M.I. is given by characteristic equation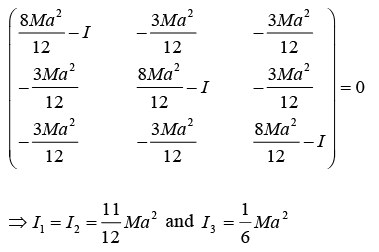
(c)
The angular momentum is given by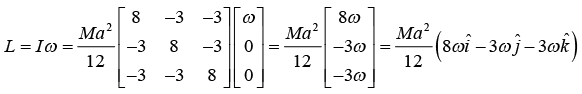
(d) If the cube is rotating about its main diagonal, then the unit vector in the direction of rotation in u = (1/√3) (1,1,1) and the angular velocity vector is ω = ωu = (ω/√3) (1,1,1) . Thus according to (10.42), the angular momentum for this case is
In this case, rotation about the main diagonal of the cube, we see that the angular momentum is in the same direction as the angular velocity.
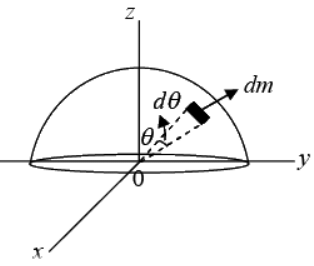
Example 18: The solid hemisphere has mass M and radius R. Find the component IZZ and IXY of inertia tensor.
x = r sinθ cos∅ y = r sinθ sin∅ z =r cosθ
dr sinθdθd∅(r2 sin2 θ cos2 ∅ + r2 sin2 θ sin2 ∅
dr sinθdθd∅.r sinθ cos∅ r sin θ sin ∅ =
|
61 videos|23 docs|25 tests
|
FAQs on Moment of Inertia - Mechanics & General Properties of Matter - Physics
| 1. What is moment of inertia and how is it calculated? |  |
| 2. What is the moment of inertia tensor? |  |
| 3. How is moment of inertia calculated for simple shapes like spheres and cylinders? |  |
| 4. Can the moment of inertia of an object change? |  |
| 5. How is the moment of inertia tensor used in engineering and physics? |  |