Moment of Inertia | Physics for Airmen Group X - Airforce X Y / Indian Navy SSR PDF Download
Moment of Inertia
Moment of inertia is like the rotational version of mass in linear motion. It’s a property of an object that makes it resist changes in its rotation or keep spinning at a steady rate.
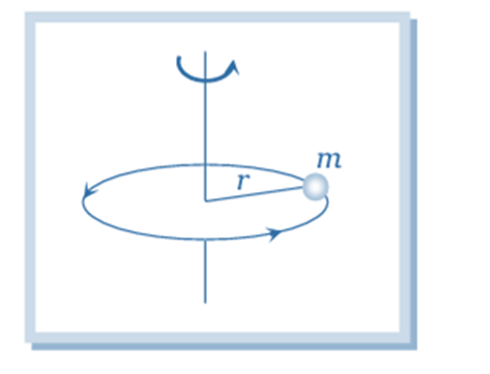
For a single particle: The moment of inertia,
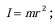 is given by , where r is the distance from the axis of rotation.
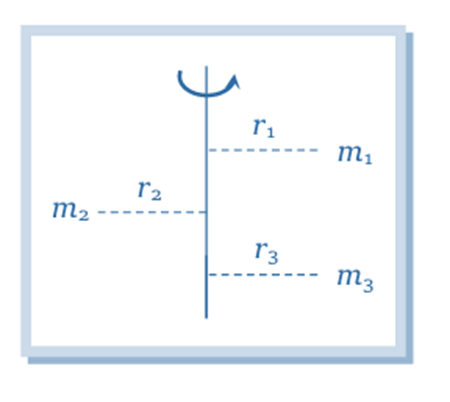
is given by , where r is the distance from the axis of rotation.For a collection of particles: The total moment of inertia of the object is the sum of the individual moments of inertia of each particle:
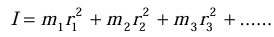
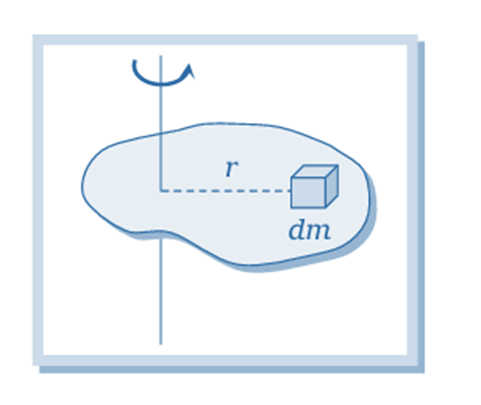
For a continuous mass distribution: If the mass is spread out continuously, we treat each tiny bit of mass, dm, as if it’s a small particle at a distance r from the axis. The moment of inertia is then
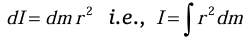
Dimension: The dimensional formula of moment of inertia is
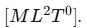
S.I. unit: The standard unit in the SI system for moment of inertia is
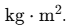
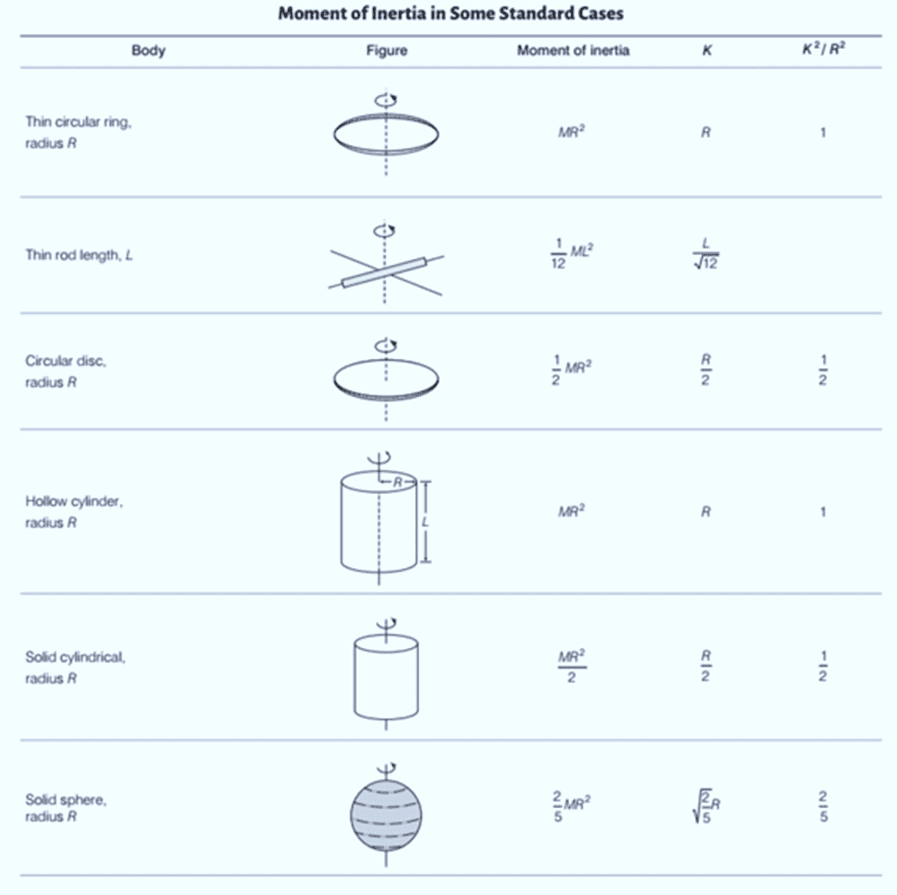
Factors Affecting Moment of Inertia: Moment of inertia depends on the mass of the object, how this mass is distributed, and the location of the axis of rotation.
Independent of Certain Factors: Moment of inertia is not affected by angular speed, angular acceleration, torque, angular momentum, or rotational kinetic energy.
Not a Vector or Scalar: Moment of inertia isn’t a vector, as it doesn’t have a specified direction (like clockwise or counterclockwise). It’s also not a simple scalar, as it can vary based on direction. It’s actually a tensor, which means it has different values depending on direction.
Hollow vs. Solid Objects: For a hollow and a solid object with the same mass, radius, and shape around the same axis, the hollow object has a larger moment of inertia. This is because the distribution of mass is farther from the axis in a hollow object.
Relationship between Rotational Kinetic Energy and Moment of Inertia
- Rotational Kinetic Energy (KE): For a rotating object, the kinetic energy can be expressed as:
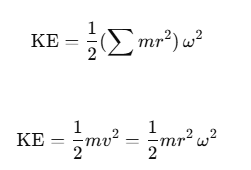
- System of Particles: For a group of n particles, the rotational kinetic energy is:
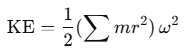
- Moment of Inertia (I): The sum
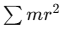 represents the moment of inertia, I, so we can write:
represents the moment of inertia, I, so we can write: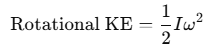
- Special Case: When ω=1, the rotational kinetic energy simplifies to:

Conclusion: Moment of inertia I is twice the rotational kinetic energy when the body is rotating with unit angular velocity:
= 2 × Rotational KE
Thus, the moment of inertia of a rigid body around an axis of rotation is numerically equal to twice the rotational kinetic energy of the body when it is rotating at a unit angular velocity about that axis.
Radius of Gyration (K)
Definition: The radius of gyration of a body around an axis is the distance from the axis where, if all the mass were concentrated, the moment of inertia would be the same as that of the actual mass distribution. It represents a “mass point” that would give the body’s moment of inertia when multiplied by the body’s total mass.
Moment of Inertia Relation: The moment of inertia III about a given axis is expressed as:
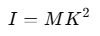
where M is the total mass of the body and K is the radius of gyration.
Formula for Radius of Gyration:
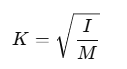
where K gives the radius of gyration for the body.
Calculating for a Rotating Body: For a system of particles with mass m at distances
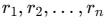 from the axis, the moment of inertia is:
from the axis, the moment of inertia is: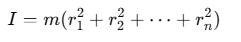
Using the definition of radius of gyration, we find:
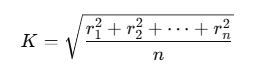
Interpretation: Radius of gyration is essentially the root mean square distance of the mass points from the axis of rotation.
Note: The radius of gyration depends on:
- The position and direction of the axis of rotation.
- The mass distribution around the axis of rotation.
Kinetic Equations of Rotational Motion about a Fixed Axis
The standard three equations of linear motionare:
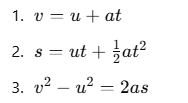
where,
v and u represent final and initial velocities,
a is the linear acceleration,
t is the time,
and s is the displacement.
Similarly, for rotational motion, we have corresponding equations:
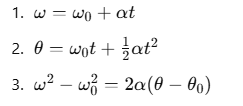
where,
ω and ω0 are the final and initial angular velocities,
α is the angular acceleration,
t is time,
θ and θ0 are the angular displacement and initial angular displacement.
These rotational equations mirror the linear motion equations but apply to objects rotating about a fixed axis.
Example 1. A Constant Angular Acceleration of a Wheel

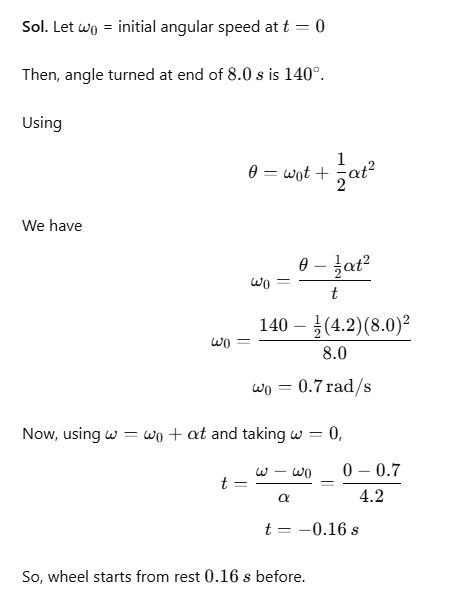
Parallel Axis Theorem
- The moment of inertia of an object about an axis through its centre of mass is the minimum moment of inertia for an axis in that direction in space.
- The moment of inertia about an axis parallel to that axis through the centre of mass is given by,
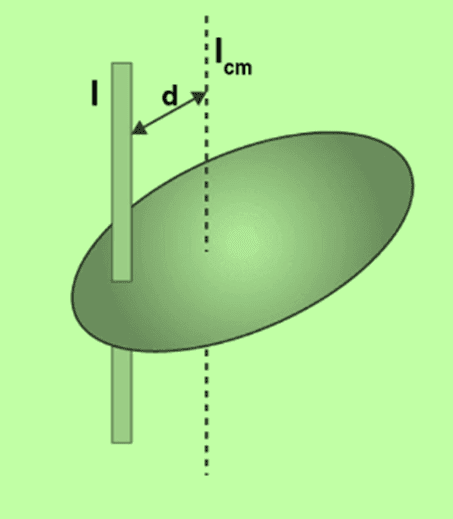
I = Icm + Md2
Where d is the distance between the two axes.
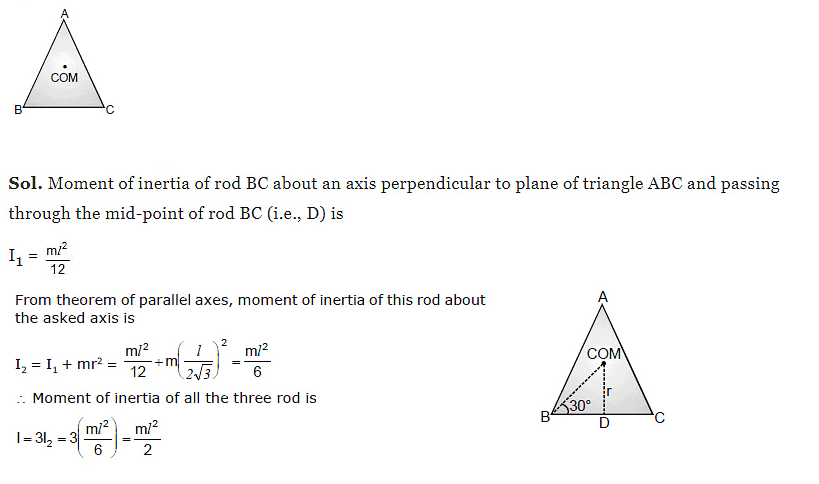
Example 2. Three rods each of mass m and length l are joined together to form an equilateral triangle as shown in figure. Find the moment of inertia of the system about an axis passing through its centre of mass and perpendicular to the plane of triangle.
Perpendicular Axis Theorem
- This theorem is applicable only to the planar bodies.
- Bodies which are flat with very less or negligible thickness.
- This theorem states that the moment of inertia of a planar body about an axis perpendicular to its plane is equal to the sum of its moments of inertia about two perpendicular axes concurrent with the perpendicular axis and lying in the plane of the body.
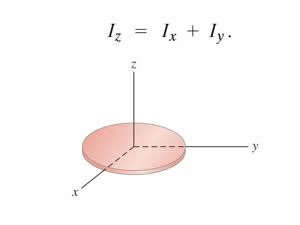
- In the above figure, we can see the perpendicular body. So Z axis is the axis which is perpendicular to the plane of the body and the other two axes lie in the plane of the body. So this theorem states that
IZ = Ix + Iy
- That means the moment of inertia about an axis which is perpendicular to its plane is equal to the sum of its moments of inertia about two perpendicular axes.
Let us see an example of this theorem:
Suppose we want to calculate the moment of inertia of a uniform ring about its diameter.
Let its centre be MR²/2, where M is the mass and R is the radius.
So, by the theorem of perpendicular axes, IZ = Ix + Iy.
Since the ring is uniform, all the diameters are equal.
∴ Ix = Iy
∴ IZ = 2 Ix
Iz = MR²/4
So finally the moment of inertia of a disc about any of its diameter is MR²/4
Solved Examples
1. From a uniform circular disc of radius R and mass 9 M, a small disc of radius R/3 is removed as shown in the figure. Calculate the moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through the centre of the disc.
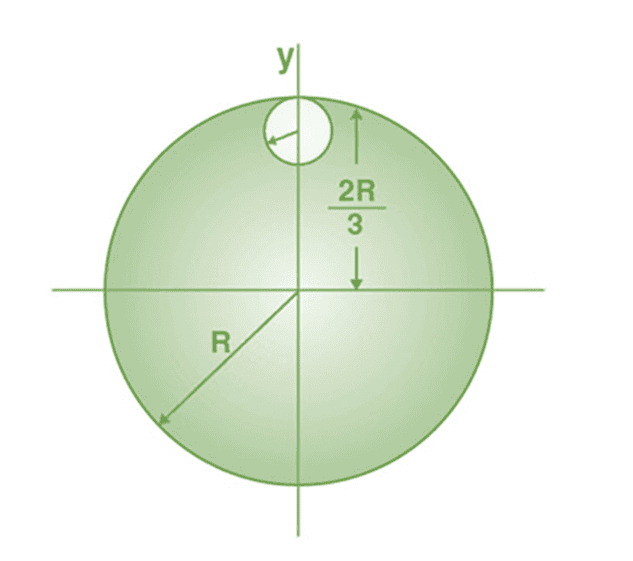
Sol:
The moment of inertia of removed part abut the axis passing through the centre of mass and perpendicular to the plane of the disc = Icm + md2
= [m × (R/3)2]/2 + m × [4R2/9] = mR2/2
Therefore, the moment of inertia of the remaining portion = moment of inertia of the complete disc – moment of inertia of the removed portion
= 9mR2/2 – mR2/2 = 8mR2/2
Therefore, the moment of inertia of the remaining portion (I remaining) = 4mR2.
2. Moment Two balls connected by a rod, as shown in the figure below (Ignore rod’s mass). Mass of ball X is 700 grams and the mass of ball Y is 500 grams. What is the moment of inertia of the system about AB?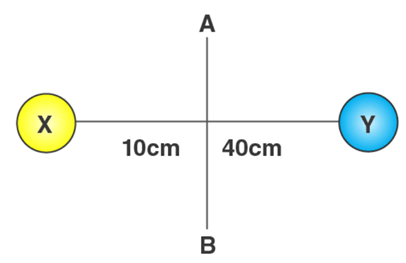
Given,
The rotation axis is AB
mX = 700 grams = 0.7 kg
mY = 500 grams = 0.5 kg
rX = 10cm = 0.1m
rY = 40cm = 0.4m
Sol:
I = mX rX2 + mY rY2
I = (0.7)× (0.1)2 + (0.5)× (0.4)2
I = (0.7) x (0.01) + (0.5) x (0.16)
I = 0.007 + o.08
I = 0.087 kg m2
Moment of inertia of the system is 0.087 kg m2
3. Two balls connected by a rod as shown in the figure below (Ignore rod’s mass). What is the moment of inertia of the system?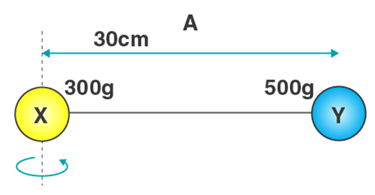
Given
mX = 300 grams = 0.3 kg
mY = 500 grams = 0.5 kg
rX = 0cm = 0m
rY = 30cm = 0.3m
Sol:
I = mX rX2 + mY rY2
I = (0.3)× (0)2 + (0.5)× (0.3)2
I = 0 + 0.045
I = 0.045 kg m2
Moment of inertia of the system is 0.045kg m2
4. The mass of each ball is 200 gram, connected by cord. The length of cord is 80 cm and the width of the cord is 40 cm. What is the moment of inertia of the balls about the axis of rotation (Ignore cord’s mass)?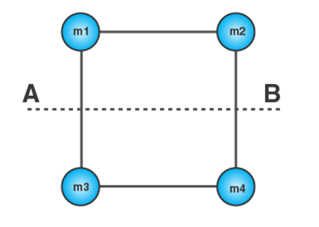
Sol:
Given
Mass of ball = m1 = m2 = m3 = m4 = 200 gram = 0.2kg
Distance between ball and the axis of rotation (r1) = 40cm = 0.4 m
Distance between ball 2 and the axis of rotation (r2) = 40 cm = 0.4 m
Distance between ball 3 and the axis of rotation (r2) = 40 cm = 0.4 m
Distance between ball 4 and the axis of rotation (r2) = 40 cm = 0.4 m
I = m1 r12 + m2 r22 + m3 r32 + m4 r42
I = (0.2) × (0.4)2 + (0.2) × (0.4 )2 + (0.2) × (0.4)2 + (0.2) × (0.4)2
I = 0.032 + 0.032 + 0.032 + 0.032
I = 0.128 kg m2
Moment of inertia of the balls about the axis o.128 kg m2
Dynamics of Rotational Motion about a Fixed Axis
The following table shows a comparison between linear (translational) motion and rotational motion around a fixed axis (e.g., the z-axis).
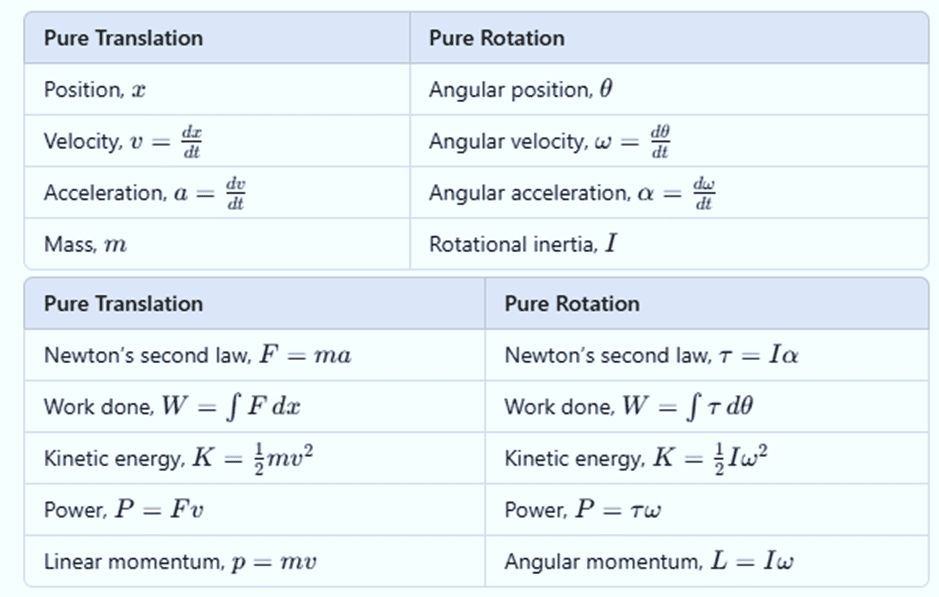
For rotational motion around a fixed axis, we consider the following:
Only forces that act in planes perpendicular to the axis of rotation are relevant, as forces parallel to the axis would produce torques perpendicular to it. We ignore these parallel forces.
Only components of position vectors that are perpendicular to the axis of rotation are considered. Any component along the axis would produce torques perpendicular to the axis and can be ignored.
Work Done by a Torque


Relation between Torque and Moment of Inertia
The rotational kinetic energy (KE) of a rigid body is given by:
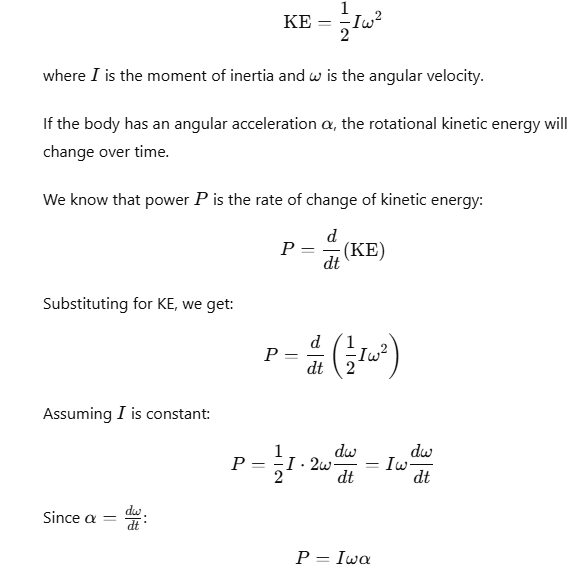
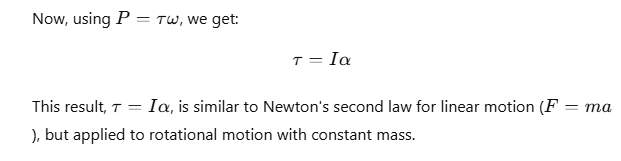
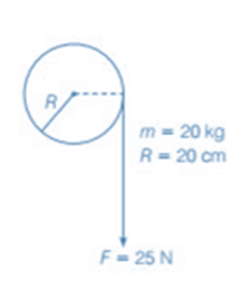
Example 2. Cord Wounded Round a Flywheel
A cord of negligible mass is wound around the rim of a flywheel of mass 20 kg and radius 20 cm. A steady pull of 25 N is applied on the cord as shown in the figure. The flywheel is mounted on a horizontal axle with frictionless bearings.
Compute angular acceleration of the flywheel.
Find the work done by the pull when 2 m of the cord is unwound.
Find also the KE of the flywheel at this point. Assume that the flywheel starts from rest.
Compare the answers of parts (ii) and (iii).
Sol:
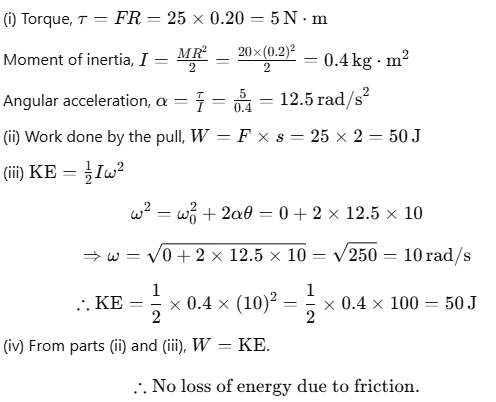
Angular Momentum in Case of Rotation about a Fixed Axis
The total angular momentumL of a system of particles rotating about a fixed axis is expressed as:


Rolling Motion
Rolling motion is a combination of pure rotation and pure translation and is commonly observed in daily life, such as the wheels of vehicles moving on a road.
In rolling motion, the translational motion of the object is represented by the movement of its center of mass.
Consider a disc rolling without slipping on a level surface. At any instant, the point of contact P0 between the disc and the surface is momentarily at rest due to the lack of slipping. If VCM is the velocity of the disc's center of mass (located at the geometric center C of the disc), then VCM is parallel to the level surface.
As the disc rotates about its center, it passes through point C. At a point P2 on the disc, the velocity v2 is the sum of the translational velocity VCM and the rotational velocity vr, where vr is the linear velocity caused by rotation.
The magnitude of the rotational linear velocity vr is given by:

Kinetic Energy of a Rolling Body
For a body rolling without slipping, the total kinetic energy is the sum of its translational and rotational kinetic energies.

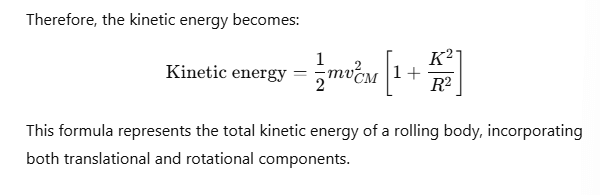
|
201 videos|410 docs|280 tests
|
FAQs on Moment of Inertia - Physics for Airmen Group X - Airforce X Y / Indian Navy SSR
| 1. What is the moment of inertia and how is it calculated for different shapes? |  |
| 2. What is the radius of gyration (K) and how is it related to the moment of inertia? |  |
| 3. How does the Parallel Axis Theorem work in calculating moment of inertia? |  |
| 4. What is the Perpendicular Axis Theorem and when can it be applied? |  |
| 5. How is work done by a torque calculated in rotational motion? |  |
















