Motion Class 9 Notes Science Chapter 7
Introduction
Rest: A body is said to be in a state of rest when its position does not change with respect to a reference point.
Motion: A body is said to be in a state of motion when its position changes continuously with reference to a point.
Describing Motion
Motion can be of different types depending upon the type of path by which the object is going through.
(i) Circulatory motion/Circular motion – In a circular path.
(ii) Linear motion – In a straight line path.
(iii) Oscillatory/Vibratory motion – To and fro path with respect to origin.
Scalar quantity: It is the physical quantity having its own magnitude but no direction.
Example: distance, speed.
Vector quantity: It is the physical quantity that requires both magnitude and direction.
Example: displacement, velocity.
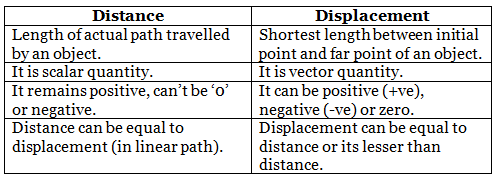
Distance and Displacement
- The actual path or length traveled by an object during its journey from its initial position to its final position is called the distance.
- Distance is a scalar quantity that requires only magnitude but no direction to explain it.
Example: Ramesh travelled 65 km. (Distance is measured by odometer in vehicles.) - Displacement is a vector quantity requiring both magnitude and direction for its explanation.
Example: Ramesh traveled 65 km southwest from Clock Tower. - Displacement can be zero (when the initial point and final point of motion are same)
Example: circular motion.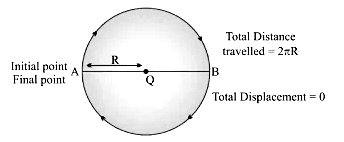
Difference between Distance and Displacement
Uniform and Non-Uniform Motion
Uniform Motion
When a body travels an equal distance in an equal interval of time, then the motion is said to be uniform motion.

Non-uniform Motion
In this type of motion, the body will travel unequal distances in equal intervals of time.
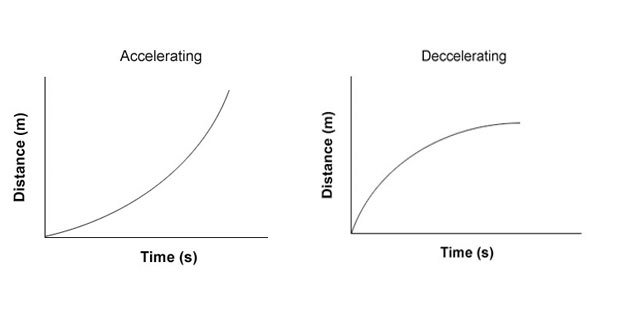
Two types of non-uniform-motion
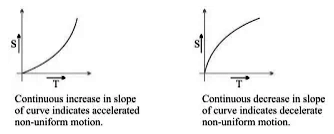
(i) Accelerated Motion: When the velocity of a body increases with time.
(ii) De-accelerated Motion: When the velocity of a body decreases with time.
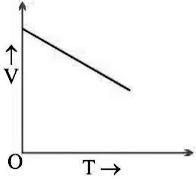
Measuring the Rate of Motion
The measurement of distance traveled by a body per unit of time is called speed.
- Speed (v) = Distance Travelled/Time Taken = s/t
- SI unit = m/s (meter/second)
- If a body is executing uniform motion, then there will be a constant speed or uniform motion.
- If a body is traveling with a non-uniform motion, then the speed will not remain uniform but have different values throughout the motion of such a body.
- For non-uniform motion, the average speed will describe one single value of speed throughout the motion of the body.
- Average speed = Total distance traveled/Total time taken
Change from km/hr to m/s = 1000m/(60×60)s = 5/18 m/s
Speed with Direction
It is the speed of a body in a given direction.
- Velocity = Displacement/Time
- Velocity is a vector quantity. Its value changes when either its magnitude or direction changes.
For non-uniform motion in a given line, average velocity will be calculated in the same way as done in average speed.
- Average velocity = Total displacement/Total time
- For uniformly changing velocity, the average velocity can be calculated as follows :
- Avg. Velocity (Avg) = (Initial velocity + Final velocity)/2 = (u+v)/2
- where, u = initial velocity, v = final velocity
- SI unit of velocity = ms-1
- Velocity = Displacement/Time
It can be positive (+ve), negative (-ve) or zero.
Rate of Change of Velocity
Acceleration is seen in non-uniform motion and it can be defined as the rate of change of velocity with time.
- Acceleration (a) = Change in velocity/Time = (v-u)/t
where, v = final velocity, u = initial velocity - If v > u, then ‘a’ will be positive (+ve).
Graphical Representation of Motion
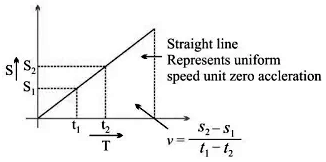
Displacement-Time Graph (s/t graph)
(i) s/t graph for uniform motion:
(ii) s/t graph for non-uniform motion:
(iii) s/t graph for a body at rest:
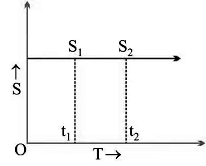
v = (s2 - s1)/(t2 - t1)
But, s2 - s1
∴ v = 0/(t2 - t1) or v=0
Velocity-Time Graph (v/t graph)
(i) v/t graph for uniform motion:
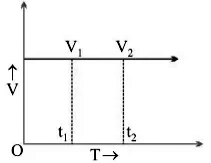
a = (v2 - v1)/(t2 - t1)
But, v2 - v1
∴ a = 0/(t2 - t1) or a = 0
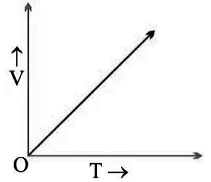
(ii) v/t graph for uniformly accelerated motion:
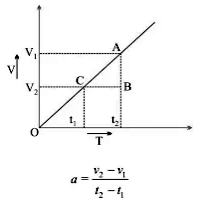
In uniformly accelerated motion, there will be an equal increase in velocity in equal intervals of time throughout the motion of the body.
(iii) v/t graph for non-uniformly accelerated motion: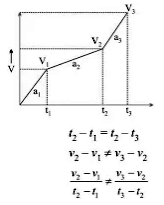
a2 ≠ a1
(iv) v/t graph for uniformly decelerated motion:
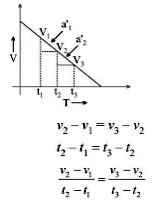
or, a1' = a2'
(v) v/t graph for non-uniformly decelerated motion:
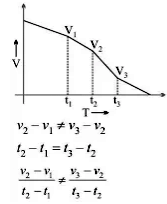
a1' ≠ a2'
Note: The area enclosed between any two-time intervals is ‘t2 - t1’ in the v/t graph, which will represent the total displacement by that body.
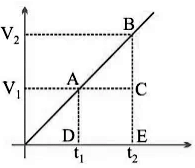
Total distance travelled by body between t2 and t1, time intervals
= Area of ∆ABC + Area of rectangle ACDB
= ½ × (v2 – v1)×(t2 - t1) + v1× (t2 - t1)
Equations of Motion
First Equation: v = u + at
Final velocity = Initial velocity + Acceleration × Time
Graphical Derivation
Suppose a body has initial velocity ‘u’ (i.e., the velocity at time t = 0 sec.) at point ‘A’, and this velocity changes to ‘v’ at point ‘B’ in ‘t’ secs. i.e., final velocity will be ‘v’.
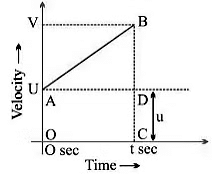
For such a body there will be an acceleration.
a = Change in velocity/Change in Time
⇒ a = (OB - OA)/(OC-0) = (v-u)/(t-0)
⇒ a = (v-u)/t
⇒ v = u + at
Second Equation: s = ut + ½ at2
Distance traveled by object = Area of OABC (trapezium)
= Area of OADC (rectangle) + Area of ∆ABD
= OA × AD + ½ × AD × BD
= u × t + ½ × t × (v – u)
= ut + ½ × t × at
⇒ s = ut + ½ at2 (∵a = (v-u)/t)
Third Equation: v2 = u2 + 2as
s = Area of trapezium OABC
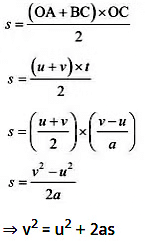
Uniform Circular Motion
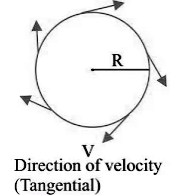
- If a body is moving in a circular path with uniform speed, then it is said to be executing uniform circular motion.
- In such a motion, the speed may be the same throughout the motion, but its velocity (which is tangential) is different at each and every point of its motion. Thus, uniform circular motion is an accelerated motion.
|
84 videos|478 docs|60 tests
|
FAQs on Motion Class 9 Notes Science Chapter 7
| 1. What is the difference between distance and displacement in motion? |  |
| 2. How can uniform and non-uniform motion be distinguished? |  |
| 3. How is speed with direction different from just speed in motion? |  |
| 4. How can the rate of change of velocity be calculated in motion? |  |
| 5. What are the equations of motion and how are they used in analyzing motion? |  |

















