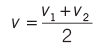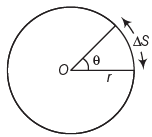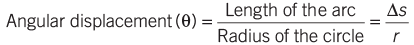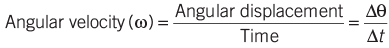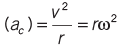Motion | General Awareness for SSC CGL PDF Download
| Table of contents |

|
| Scalar and Vector Quantities |

|
| Dimensions |

|
| Kinematics |

|
| Rest and Motion |

|
| Distance and Displacement |

|
| Speed |

|
| Velocity |

|
| Acceleration |

|
| Projectile Motion |

|
| Circular Motion |

|
| Force |

|
| Newton’s Laws |

|
Scalar and Vector Quantities
Physical quantities are categorized based on their magnitudes and direction:
- Scalars: Quantities that have only magnitude and no direction (e.g., length, mass, time).
- Vectors: Quantities that have both magnitude and direction (e.g., force, displacement, impulse). Vectors obey the triangle law and parallelogram law of addition. Special types of vectors include zero (or null) vectors and unit vectors.
Dimensions

- Dimensions of a physical quantity are the powers to which the fundamental units are raised to obtain the units of that quantity.
- Fundamental quantities include mass (M), length (L), time (T), temperature (θ), luminous intensity (cd), amount of substance (N), and current (A).
- The dimension of a physical quantity is written as [MaLbTcθd], where a, b, c, and d are exponents.
- where, a, b, c, and d are exponents.
Some Important dimensional Formulae are
Kinematics
Kinematics, a branch of mechanics, studies the motion of objects without considering the causes of their motion.
Rest and Motion
An object is at rest if it does not change its position relative to its surroundings over time. It is in motion if it changes its position relative to its surroundings over time.
- Rectilinear Motion: Motion along a straight line (e.g., a moving car, motion under gravity).
- Angular Motion: Motion along a curved path (e.g., circular motion, projectile motion).
- Rotational Motion: Motion around a fixed axis (e.g., a rotating fan).
Distance and Displacement
- Distance: The length of the actual path traveled by an object. It is a scalar quantity.
- Displacement: The change in position of the object in a particular direction. It is a vector quantity and can be positive, negative, or zero.
- An object is in uniform motion if it travels equal distances in equal intervals of time, and in non-uniform motion if it travels unequal distances in equal intervals of time.
Speed
The distance covered by a moving body per unit time.
- Instantaneous Speed: Speed at a specific instant.
- Uniform Speed: Equal distances covered in equal time intervals.
- Non-Uniform Speed: Unequal distances covered in equal time intervals.
- Average Speed: Total distance traveled divided by the total time taken.
For equal distances at speeds v1 and v2, average speed is the harmonic mean of the two speeds. For equal times at speeds v1 and v2, average speed is the arithmetic mean of the two speeds.
For equal times at speeds v1 and v2, average speed is the arithmetic mean of the two speeds.
Velocity
The rate of change of displacement per unit time.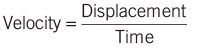
- Instantaneous Velocity: Velocity at a specific instant.
- Uniform Velocity: Equal displacements covered in equal time intervals.
- Non-Uniform Velocity: Unequal displacements covered in equal time intervals.
- Average Velocity: Total displacement divided by the total time taken.

Acceleration
The rate of change of velocity per unit time. It is a vector quantity with SI unit m/s².
- Instantaneous Acceleration: Acceleration at a specific instant.
- Positive Acceleration: Velocity increases with time.
- Negative Acceleration (Deceleration or Retardation): Velocity decreases with time.
- Constant Acceleration: Acceleration does not change with time.
Equations of Uniformly Accelerated Motion (Along a Straight Line)
For an object with initial velocity u, final velocity v after time t, constant acceleration a, and distance traveled s: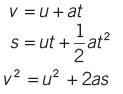
For free-falling objects under gravity, replace a with g. For objects thrown upward, replace a with −g. Distance traveled in the n-th second: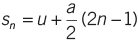
Graphical Representations
- For zero acceleration or constant speed, the velocity-time graph is parallel to the time axis. For accelerating or decelerating bodies, the graph is a straight line inclined to the time axis.
- The position-time graph for accelerating or decelerating bodies is parabolic.
- The acceleration-time graph for uniformly accelerating bodies is parallel to the time axis.
- For uniform acceleration, the position-velocity graph is parabolic, and the velocity-time graph is a straight line.
- The slope of the displacement-time graph gives velocity, while the slope of the velocity-time graph gives acceleration.
Projectile Motion
When a body is thrown at an angle θ (excluding 90°) to the horizontal, its motion under gravity follows a curved parabolic path known as a trajectory. This type of motion is called projectile motion.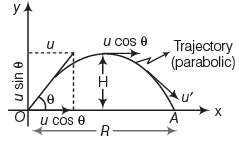
- The horizontal component of the velocity (ucosθ) remains constant and drives the horizontal motion.
- The vertical component of the velocity (usinθ) is responsible for the vertical motion.
Examples include:
- The motion of a bullet shot from a gun.
- The motion of a rocket after burnout.
- The motion of a bomb dropped from an airplane.
Key Terms in Projectile Motion
- Time of Flight (T): The time taken by the projectile to travel from the point of projection (O) to the endpoint (A).

- Maximum Height (H): The highest point reached by the projectile during its journey from O to A.

- Range (R): The horizontal distance between the starting point (O) and the final point (A).

Properties of Projectile Motion
- The horizontal range is maximized when the angle of projection is 45°. The range is the same for angles θ and (90° − θ).
- The horizontal component of velocity remains constant throughout the motion. At the highest point of the trajectory, the vertical component of velocity is zero, making the direction of motion horizontal.
- If a ball is dropped from a height while another is thrown horizontally at the same time, both balls will hit the ground simultaneously but at different locations.
Circular Motion
The motion of an object along a circular path is called circular motion.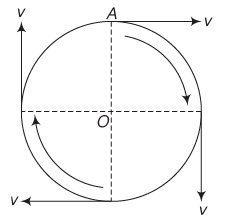
- Uniform Circular Motion: Circular motion at a constant speed. The direction of motion at any point is given by the tangent to the circle at that point. Both velocity and acceleration change in uniform circular motion.
- Non-Uniform Circular Motion: The speed varies at different points on the circular path.
Angular Displacement and Velocity
- Angular Displacement: The angle subtended at the center of the circle by a body moving along the circumference. Its unit is the radian (rad).


- The time rate of change of angular displacement is called angular velocity. Its unit is rad s−1.

- If time period of uniform circular motion is T, then average angular velocity is given by

- Linear velocity in circular motion is given by Linear velocity = Angular velocity × radius or v = ω × r
Centripetal Acceleration
During circular motion, an acceleration directed towards the center acts on the body, known as centripetal acceleration.
- Centripetal acceleration (ac) is given by:
 where v is the uniform speed of the body, r is the radius of the circular path, and ω is the angular velocity.
where v is the uniform speed of the body, r is the radius of the circular path, and ω is the angular velocity. - The direction of centripetal acceleration is always towards the center of the circular path.
Force
It is an external push or pull which can change or tries to change the state of rest or of uniform motion. SI unit is newton (N) and CGS unit is dyne. 1 N = 105 dyne.
If sum of all the forces acting on a body is zero, then body is said to be in equilibrium.
Four fundamental forces in nature:
- Gravitational force
- Electromagnetic force
- Weak nuclear force
- Strong nuclear force (the strongest of the four)
Centripetal Force
During circular motion, a force directed towards the center of the circular path acts on the body, known as centripetal force.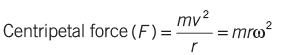
where, m = mass of the body.
Centrifugal Force
In circular motion, a force appears to act outwardly opposite to the centripetal force, called centrifugal force. This is an apparent or pseudo force.
Applications of Centripetal and Centrifugal Forces
- Cyclists incline from vertical to obtain the required centripetal force, slow down to take safe turns, and move on a larger radius path to balance reduced friction due to bending.
- Roads are banked at turns to provide the necessary centripetal force, with the normal reaction force component contributing to this force.
- Frictional force between vehicle tires and the road acts as centripetal force during a turn on a curved road.
- If a car exceeds the safe speed limit on a turn, the inner tires, experiencing a larger centrifugal force due to a smaller radius, may skid.
- When a bucket of water is revolved rapidly in a vertical plane, centrifugal force prevents water from falling out, even when inverted.
- Electrostatic force acts as centripetal force for the orbital motion of electrons around the nucleus.
- During the rotation of milk, lighter cream particles move towards the center while heavier milk particles move to the circumference, resulting in cream separation.
- The gravitational force between the Earth and the Sun acts as the centripetal force for Earth's revolution around the Sun.
- Torque is the product of force and the perpendicular distance from the axis of rotation, producing a rotational effect. It is a vector quantity.
Newton’s Laws
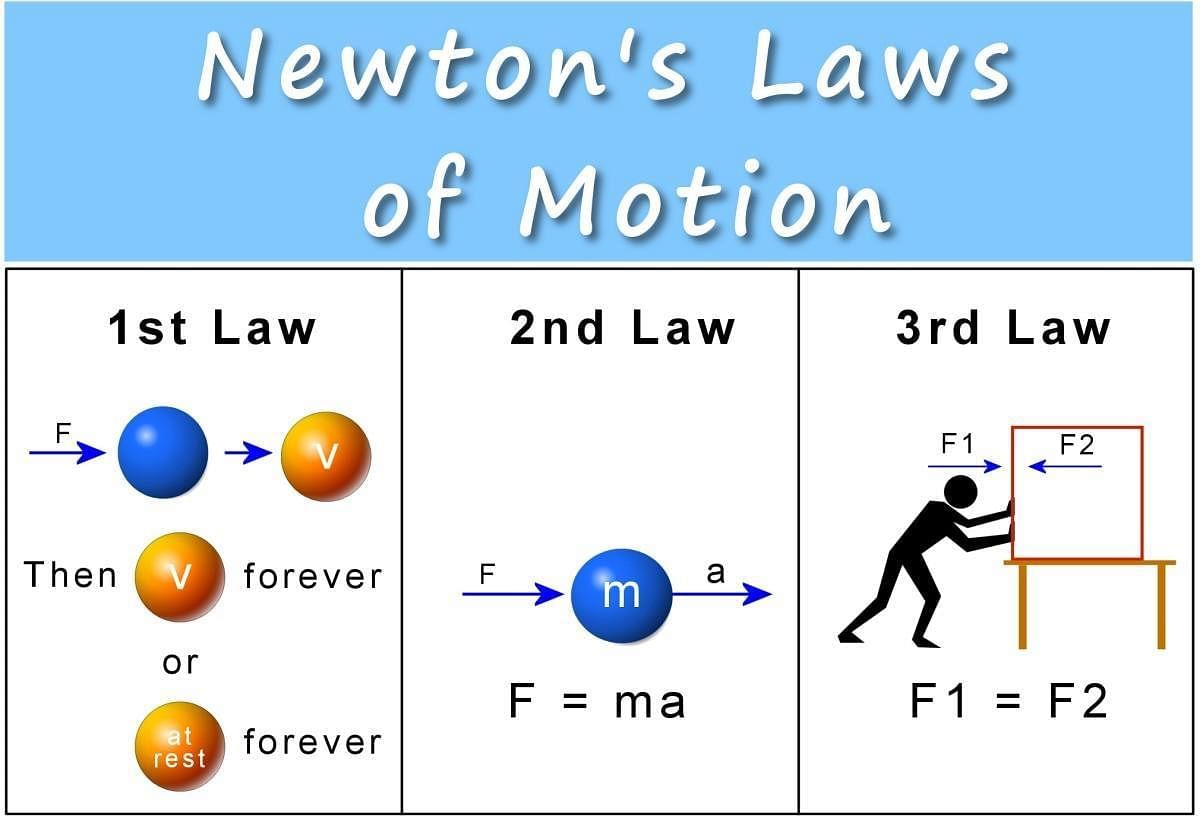
Newton’s First Law
A body remains in its state of rest or uniform motion in a straight line unless acted upon by an external force. Inertia is the property that opposes changes in this state.
Inertia of Rest: A body cannot change its state of rest on its own. For example:
- Passengers in a stationary bus or train lurch backward when it starts moving due to inertia of rest.
- Dust particles come off a carpet when beaten because of inertia of rest.
- A person jumping from a moving vehicle is advised to jump forward and run to counter inertia of rest.
Inertia of Motion: A body cannot change its state of uniform motion on its own. For example:
- Passengers in a moving bus or train lurch forward when it stops suddenly due to inertia of motion.
Momentum
Momentum is the product of an object's mass and velocity, with units of kg·m/s. It is a vector quantity, and its direction is the same as the velocity of the object.
Momentum = Mass × Velocity p = m × vConservation of Linear Momentum
The linear momentum of a system of particles remains conserved if no external force acts on the system. Rocket propulsion and jet engines operate based on this principle, where the ejected gas provides a forward force that propels the rocket.Conservation of Angular Momentum
Angular momentum remains conserved if no external torque acts on the system, according to the principle of conservation of angular momentum.
Newton’s Second Law
The rate of change of momentum of a body is directly proportional to the applied force, and this change occurs in the direction of the applied force.
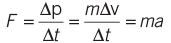
where m is the mass of the body (constant). A body is in equilibrium if the resultant force on it is zero.
Newton’s Third Law
For every action, there is an equal and opposite reaction, and these forces act on two different objects. Rocket propulsion is an example of Newton’s third law in action.
|
464 videos|571 docs|394 tests
|
FAQs on Motion - General Awareness for SSC CGL
| 1. What is the difference between scalar and vector quantities in kinematics? |  |
| 2. How does acceleration affect the motion of an object in kinematics? |  |
| 3. What is the difference between distance and displacement in kinematics? |  |
| 4. How does projectile motion differ from circular motion in kinematics? |  |
| 5. How do dimensions play a role in kinematics? |  |

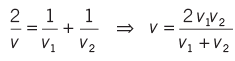 For equal times at speeds v1 and v2, average speed is the arithmetic mean of the two speeds.
For equal times at speeds v1 and v2, average speed is the arithmetic mean of the two speeds.