MULTIPLE CHOICE QUESTIONS
Q.1. The angle between 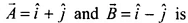
(a) 45°
(b) 90°
(c) –45°
(d) 180°
Ans. (b)
Solution.
Given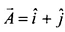
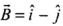

∴ θ = 90º
Q.2. Which one of the following statements is true?
(a) A scalar quantity is the one that is conserved in a process.
(b) A scalar quantity is the one that can never take negative values.
(c) A scalar quantity is the one that does not vary from one point to another in space.
(d) A scalar quantity has the same value for observers with different orientations of the axes.
Ans. (d)
Solution.
A scalar quantity is independent of direction hence has the same value for observers with different orientations of the axes.
For example, a car is traveling along +x axis, it travels 10 m. If the same car is moving with the same speed for the same time interval along -x axis, then the distance meter of car shows the same travelled distance. The path length is same in both the cases.
Q.3. Figure shows the orientation of two vectors u and v in the XY plane.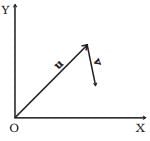

Which of the following is correct?
(a) a and p are positive while b and q are negative.
(b) a, p and b are positive while q is negative.
(c) a, q and b are positive while p is negative.
(d) a, b, p and q are all positive.
Ans.
Solution.
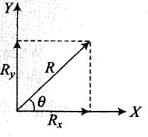
Key concept: Resolution of Vector into Components:
Consider a vector 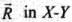 plane as shown in figure. If we draw orthogonal vectors
plane as shown in figure. If we draw orthogonal vectors
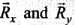 along x and y axes respectively, by law of vector addition,
along x and y axes respectively, by law of vector addition, 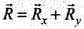
 Now as for any vector
Now as for any vector 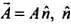 is the direction of
is the direction of 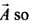
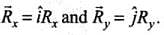
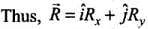 ...(i)
...(i)
But from figure, Rx = R cos θ ..(ii)
and Ry = R sin θ ....(ii)
Since R and θ are usually known, equations (ii) and (iii) give the magnitude o f the components of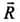 along x- and y-axes respectively.
along x- and y-axes respectively.
Here it is worthy to note once a vector is resolved into its components, the components themselves can be used to specify the vector as:
(1) The magnitude of the vector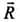 is obtained by squaring and adding equations (ii) and (iii), i.e.
is obtained by squaring and adding equations (ii) and (iii), i.e.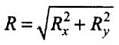
(2) The direction of the vector 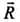 is obtained by dividing equation (iii) by (ii), i.e.
is obtained by dividing equation (iii) by (ii), i.e.
tan θ = (Ry/Rx) or θ = tan-1(Ry/Rx)
In such type of problems we have to resolve the rectangular components according to the diagram.
Clearly from the diagram 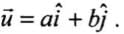
As u is in the first quadrant, hence both of its components a and b will be positive and as v is in fourth quadrant. For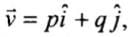 as it is in positive x-direction and located downward hence x-component p will be positive and y-component q will be negative.
as it is in positive x-direction and located downward hence x-component p will be positive and y-component q will be negative.
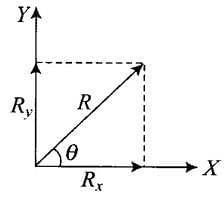
Q.4. The component of a vector r along X-axis will have maximum value if
(a) r is along positive Y-axis
(b) r is along positive X-axis
(c) r makes an angle of 45° with the X-axis
(d) r is along negative Y-axis
Ans. (b)
Solution.
Consider a vector  plane as shown in figure. If we draw orthogonal vectors
plane as shown in figure. If we draw orthogonal vectors
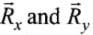 along x and y axes respectively, by law of vector addition,
along x and y axes respectively, by law of vector addition,
 The magnitude of component of r along A-axis
The magnitude of component of r along A-axis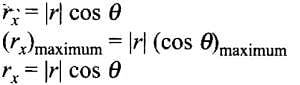
 (∵ cos θ is maximum if θ = 0°)
(∵ cos θ is maximum if θ = 0°)
As θ = 0°, r is along positive x-axis.
Q.5. The horizontal range of a projectile fired at an angle of 15° is 50 m. If it is fired with the same speed at an angle of 45°, its range will be
(a) 60 m
(b) 71 m
(c) 100 m
(d) 141 m
Ans. (c)
Solution.
The horizontal range of the projectile fired at an angle is given by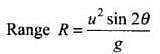
Where, θ is the angle of projection, u is the initial velocity with which the projectile is fired, and g is the gravitational acceleration.
According to the problem the angle of projection, θ = 15° and horizontal range, R = 50 m By substituting the values in the above relation, we get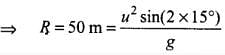
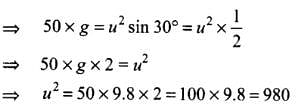
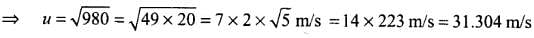
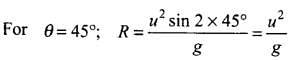 (∵ sin 90º = 1)
(∵ sin 90º = 1)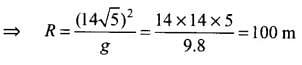
Q.6. Consider the quantities, pressure, power, energy, impulse, gravitational potential, electrical charge, temperature, area. Out of these, the only vector quantities are
(a) Impulse, pressure and area
(b) Impulse and area
(c) Area and gravitational potential
(d) Impulse and pressure
Ans. (b)
Solution.
We know that impulse J = F. ∆t = ∆p, where F is force, At is time duration and Ap is change in momentum. As ∆p is a vector quantity, hence impulse is also a vector quantity. Sometimes area can also be treated as vector direction of area vector is perpendicular to its plane.
Q.7. In a two dimensional motion, instantaneous speed v0 is a positive constant. Then which of the following are necessarily true?
(a) The average velocity is not zero at any time.
(b) Average acceleration must always vanish.
(c) Displacements in equal time intervals are equal.
(d) Equal path lengths are traversed in equal intervals.
Ans. (d)
Solution.
Speed (Instantaneous Speed): The magnitude of the velocity at any instant of time is known as Instantaneous Speed or simply speed at that instant of time. It is denoted by v.
Quantitatively: Speed = distance/time
Mathematically, it is the time rate at which distance is being travelled by the particle.
- Speed is a scalar quantity. It can never be negative (as shown by speedometer of our vehicle).
- Instantaneous speed is the speed of a particle at a particular instant of time.
Hence, Total distance travelled = Path length = (speed) x time taken Important point: We should be very careful with the fact that speed is related with total distance covered not with displacement.
Q.8. In a two dimensional motion, instantaneous speed v0 is a positive constant. Then which of the following are necessarily true?
(a) The acceleration of the particle is zero.
(b) The acceleration of the particle is bounded.
(c) The acceleration of the particle is necessarily in the plane of motion.
(d) The particle must be undergoing a uniform circular motion.
Ans. (c)
Solution.
This motion is two dimensional and given that instantaneous speed v0 is positive constant. Acceleration is defined as the rate of change of velocity (instantaneous speed), hence it will also be in the plane of motion.
Q.9. Three vectors A,B and C add up to zero. Find which is false.
(a) (A×B) × C is not zero unless B,C are parallel
(b) (A×B).C is not zero unless B,C are parallel
(c) If A,B,C define a plane, (A×B)×C is in that plane
(d) (A×B).C=|A||B||C|→ C2 = A2 + B2
Ans. (c)
Solution.
These types of problems can be solved by hit and trial method by picking up options one by one
Sum of vectors is given as 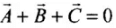
Hence, we can say that A, B and C are in one plane and are represented by the three sides of a triangle taken in one order. Let us discuss all the options one by one.
(a) We can write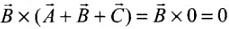
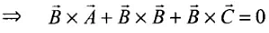
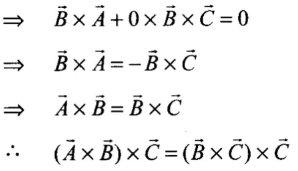
It cannot be zero.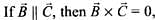 then
then 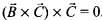 Even if
Even if 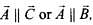 then also the cross product in any manner will be zero. So, option (a) is not false.
then also the cross product in any manner will be zero. So, option (a) is not false.
(b) 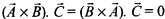 whatever be the positions of
whatever be the positions of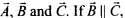 then
then 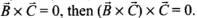 So, option (b) is not false.
So, option (b) is not false.
(c)  and the direction of X is perpendicular to the plane containing
and the direction of X is perpendicular to the plane containing 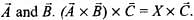 Its direction is in the plane of
Its direction is in the plane of 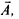
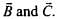 So, option (c) is false.
So, option (c) is false.
(d) 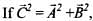 then angle between
then angle between 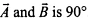
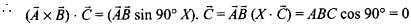
Hence, option (d) is not false.
Q.10. It is found that |A+B|=|A|.This necessarily implies,
(a) B = 0
(b) A,B are antiparallel
(c) A,B are perpendicular
(d) A.B ≤ 0
Ans. (b)
Solution.
According to the problem,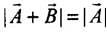
By squaring both sides, we get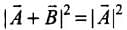
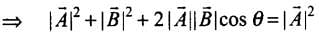
where θ is the angle between 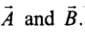
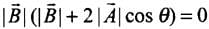
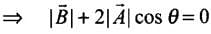
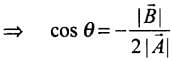
If A and B are antiparallel, then θ = 180°
Hence from Eq. (i),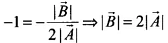
Hence, correct answer will be 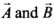 are antiparallel provided
are antiparallel provided 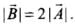
It seems like option (a) is also correct but it is not for either
either 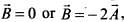 so this option will be false.
so this option will be false.
Q.11. Two particles are projected in air with speed vo at angles θ1 and θ2 (both acute) to the horizontal, respectively. If the height reached by the first particle is greater than that of the second, then tick the right choices
(a) Angle of projection : q1 > q2
(b) Time of flight : T1 > T2
(c) Horizontal range : R1 > R2
(d) Total energy : U1 > U2
Ans. (a, b)
Solution.
Maximum height H of projectile
From here H ∝ Sin2θ
For Projectile 1, θ = θ1
For Projectile 2,θ = θ2
u1 = vo u2 = vo
(a) H1 > H2 (Given)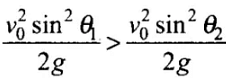
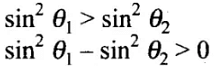

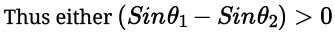
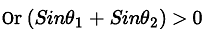
⇒ θ1 and θ2 lies between sin θ1 > θ2
0° to 90° i.e., acute as given θ1 > θ2 ...(i)
So option (a) is correct.
(b) we know time of flight: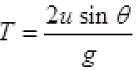
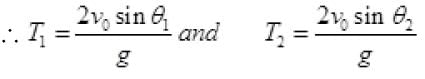
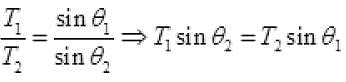
As sin θ1 > sin θ2
∴ T1 > T2
So, Option (b) is also correct.
(c) we know that range, 
R1 is the range of the first particle. R2 is the range of the second particle.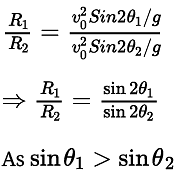
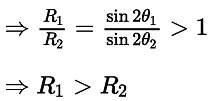
But if θ1 + θ2 = 90°,then R1 = R2
Hence option (c) is incorrect.
(d) we know that total energy(U) = P.E+K.E
For particle 1,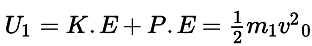
For particle 2,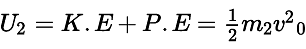
if m1 = m2 = m & as H1 > H2
We know at the highest point the total energy is equal to the P.E.
∴ PE1 > PE2 or U1 > U2
So it does not verify option (d).
Hence Option(a,b) is correct.
Q.12. A particle slides down a frictionless parabolic(y = x2) track (A – B – C) starting from rest at point A (Fig.). Point B is at the vertex of parabola and point C is at a height less than that of point A. After C, the particle moves freely in air as a projectile. If the particle reaches highest point at P, then (a) KE at P = KE at B
(a) KE at P = KE at B
(b) Height at P = height at A
(c) Total energy at P = total energy at A
(d) Time of travel from A to B = time of travel from B to P
Ans. (c)
Solution.
Key concept: In such type of problems, we have to observe the nature of track that if there is a friction or not, as friction is not present in this track, total energy of the particle will remain constant throughout the journey.
According to the problem, the path traversed by the particle on a frictionless track is parabolic, is given by the equation y = x2, thus total energy (KE + PE) will be same throughout the journey.
Hence, total energy at A = total energy at P
At B the particle is having only KE but at P some KE is converted to PE.
So, (KE)B > (KE)P
Total energy at A = PE = Total energy at B = KE = Total energy at P = PE + KE
The potential energy at A is converted to KE and PE at P, hence (PE)P < (PE)A
Hence, (Height) P < (Height) A
As, Height of P < Height of A
Hence, path length AB > path length BP
Hence, time of travel from A to B ≠ Time of travel from B to P.
Q.13. Following are four differrent relations about displacement, velocity and acceleration for the motion of a particle in general. Choose the incorrect one (s):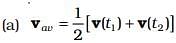
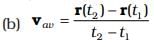
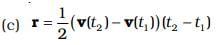
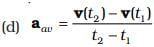
Ans. (a, c)
Solution.
When an object covers a displacement Δr in time Δt, its average velocity is given by 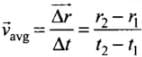 where r1 and r2 are position vectors corresponding to time t1, and t2.
where r1 and r2 are position vectors corresponding to time t1, and t2.
If the velocity of an object changes from v1 to v2 in time Δt, average acceleration is given by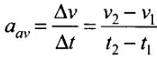
But, when acceleration is non-uniform,
Option (c) is similar to the relation 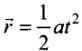 which is not correct if initial velocity is given.
which is not correct if initial velocity is given.
So (b) and (d) are the correct relations for the uniform acceleration.
Q.14. For a particle performing uniform circular motion, choose the correct statement(s) from the following:
(a) Magnitude of particle velocity (speed) remains constant.
(b) Particle velocity remains directed perpendicular to radius vector.
(c) Direction of acceleration keeps changing as particle moves.
(d) Angular momentum is constant in magnitude but direction keeps changing.
Ans. (a, b, c)
Solution.
While a particle is in uniform circular motion. Then the following statements are true.
(i) speed will be always constant throughout.
(ii) velocity will be always tangential in the direction of motion at a particular point.
(iii) the centripetal acceleration a = v2/r and its direction will always towards centre of the circular trajectory.
(iv) angular momentum (mvr) is constant in magnitude and direction. And its direction is perpendicular to the plane containing r and v.
Important point: In uniform circular motion, magnitude of linear velocity and centripetal acceleration is constant but direction changes continuously.
Q.15. For two vectors A and B, |A + B| = |A - B| is always true when
(a) |A| = |B| ≠ 0
(b) A ⊥ B
(c) |A| = |B| ≠ 0 and A and B are parallel or anti parallel
(d) when either |A| or |B| is zero
Ans. (b, d)
Solution. According to the problem,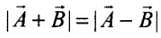

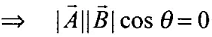
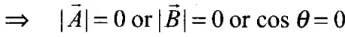
i.e. θ = 90°
When θ = 90°, we can say that 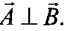
Hence options (b) and (d) are correct.
VERY SHORT ANSWER TYPE QUESTIONS
Q.1. A cyclist starts from centre O of a circular park of radius 1km and moves along the path OPRQO as shown Fig. If he maintains constant speed of 10ms–1, what is his acceleration at point R in magnitude and direction?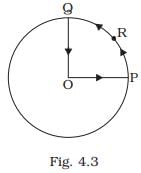 Ans. According to the problem the path of the cyclist is O-P- R-Q-O.
Ans. According to the problem the path of the cyclist is O-P- R-Q-O.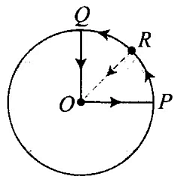 The cyclist is in uniform circular motion and it is given that linear velocity = 10 m/s, R = 1 km = 1000 m. As we know whenever an object is performing circular motion, acceleration is called centripetal acceleration and is always directed towards the centre. So cyclist experiences a centripetal force (acceleration) at point R towards centre.
The cyclist is in uniform circular motion and it is given that linear velocity = 10 m/s, R = 1 km = 1000 m. As we know whenever an object is performing circular motion, acceleration is called centripetal acceleration and is always directed towards the centre. So cyclist experiences a centripetal force (acceleration) at point R towards centre.
The centripetal acceleration at R is given by the relation,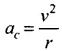
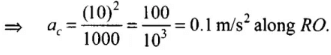
Q.2. A particle is projected in air at some angle to the horizontal, moves along parabola as shown in Fig, where x and y indicate horizontal and vertical directions, respectively. Show in the diagram, direction of velocity and acceleration at points A, B and C.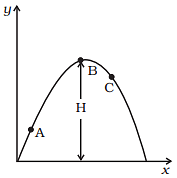 Ans. In projectile motion horizontal component of velocity will always be constant and acceleration is always vertically downward and is equal to g. Direction of velocity will always be tangential to the curve in the direction of motion.
Ans. In projectile motion horizontal component of velocity will always be constant and acceleration is always vertically downward and is equal to g. Direction of velocity will always be tangential to the curve in the direction of motion.
As shown in the diagram in which a particle is projected at an angle 0.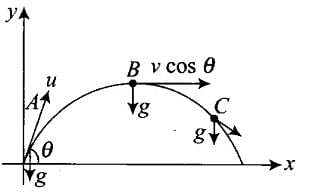 vx = Horizontal component of velocity
vx = Horizontal component of velocity
= v cos θ = constant.
vy = Vertical component of velocity
= v sinθ
Q.3. A ball is thrown from a roof top at an angle of 45° above the horizontal. It hits the ground a few seconds later. At what point during its motion, does the ball have
(a) Greatest speed.
(b) Smallest speed.
(c) Greatest acceleration?
Ans. A ball is projected from O at an angle of 450 with horizontal. From O to A body rises up, height increases so its speed & hence KE (speed) decreases.From A to B it’s speed again increases as its height decreases equal to its’s initial speed at O, because O and B are on the same horizontal line.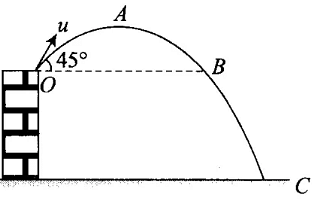 From B to C, its height again decreases so its speed from B to C increases and become maximum at C vy maximum. vx = u cos 450 = u/√2 m/s is always constant at any point.
From B to C, its height again decreases so its speed from B to C increases and become maximum at C vy maximum. vx = u cos 450 = u/√2 m/s is always constant at any point.
Hence, (a) greatest speed of ball is at C as vy maximum and vx = u/√2
(b) the smallest speed will be at A where maximum height and the vy = 0 has the only horizontal speed of constant value u/√2
(c) As the force acting on the ball is only due to gravitational force downward and is constant so acceleration is also constant downward and always equal to ‘g’.
Q.4. A football is kicked into the air vertically upwards. What is its (a) acceleration, and (b) velocity at the highest point?
Ans. (a) The situation is shown in the diagram below in which a football is kicked into the air vertically upwards. Acceleration of the football will always be vertical downward and is called acceleration due to gravity (g).
(b) When the football reaches the highest point it is momentarily at rest and at that moment its velocity will be zero as it is continuously retarded by acceleration due to gravity (g).
Q.5. A, B and C are three non-collinear, non co-planar vectors. What can you say about direction of A × (B × C)?
Ans. The direction of the vector 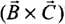 will be perpendicular to the plane containing by vectors
will be perpendicular to the plane containing by vectors  by Right-hand thumb or Right-hand grip rule (RHGR).
by Right-hand thumb or Right-hand grip rule (RHGR).
The direction of the vector 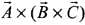 will be perpendicular to
will be perpendicular to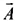 and in a plane containing
and in a plane containing  by Right-hand grip rule.
by Right-hand grip rule.
FAQs on NCERT Exemplar: Motion in a Plane- 1 - JEE
| 1. What is motion in a plane? |  |
| 2. How is motion in a plane different from motion in a straight line? |  |
| 3. What are the different types of motion in a plane? |  |
| 4. How can we analyze motion in a plane mathematically? |  |
| 5. How is motion in a plane relevant to JEE (Joint Entrance Exam)? |  |

|
Explore Courses for JEE exam
|

|

















