NCERT Exemplar: Application of Derivatives- 1 | Mathematics (Maths) for JEE Main & Advanced PDF Download
Q.1. A spherical ball of salt is dissolving in water in such a manner that the rate of decrease of the volume at any instant is proportional to the surface. Prove that the radius is decreasing at a constant rate.
Ans.
Ball of salt is spherical
∴ Volume of ball,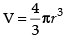 where r = radius of the ball
where r = radius of the ball
As per the question,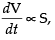 where S = surface area of the ball
where S = surface area of the ball
⇒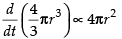 [∵ S = 4pr2]
[∵ S = 4pr2]
⇒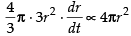
⇒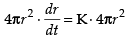 (K = Constant of proportionality)
(K = Constant of proportionality)
⇒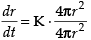
∴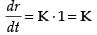
Hence, the radius of the ball is decreasing at constant rate.
Q.2. If the area of a circle increases at a uniform rate, then prove that perimeter varies inversely as the radius.
Ans.
We know that:
Area of circle, A = πr2, where r = radius of the circle.
and perimeter = 2πr
As per the question,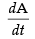 = K, where K = constant
= K, where K = constant
⇒
∴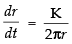 ...(1)
...(1)
Now Perimeter c = 2πr
Differentiating both sides w.r.t., t, we get
⇒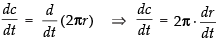
⇒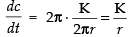 [From (1)]
[From (1)]
⇒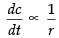
Hence, the perimeter of the circle varies inversely as the radius of the circle.
Q.3. A kite is moving horizontally at a height of 151.5 meters. If the speed of kite is 10 m/s, how fast is the string being let out; when the kite is 250 m away from the boy who is flying the kite? The height of boy is 1.5 m.
Ans.
Given that height of the kite (h) = 151.5 m
Speed of the kite(V) = 10 m/s
Let FD be the height of the kite and AB be the height of the boy.
Let AF = x m
∴ BG = AF = x
m and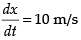
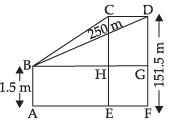
From the figure, we get that
GD = DF – GF ⇒ DF - AB
= (151.5 – 1.5) m = 150 m [∵ AB = GF]
Now in ΔBGD,
BG2 + GD2 = BD2 (By Pythagoras Theorem)
⇒ x2 + (150)2 = (250)2
⇒ x2 + 22500 = 62500 ⇒ x2 = 62500 – 22500
⇒ x2 = 40000 ⇒ x = 200 m
Let initially the length of the string be y m
∴ In ΔBGD
BG2 + GD2 = BD2 ⇒ x2 + (150)2 = y2
Differentiating both sides w.r.t., t, we get
⇒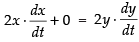
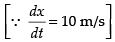
⇒ 2 x 200 x 10 = 2 x 250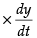
∴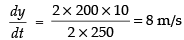
Hence, the rate of change of the length of the string is 8 m/s.
Q.4. Two men A and B start with velocities v at the same time from the junction of two roads inclined at 45° to each other. If they travel by different roads, find the rate at which they are being separated.
Ans.
Let P be any point at which the two roads are inclined at an angle of 45°.
Two men A and B are moving along the roads PA and PB respectively with the same speed ‘V’.
Let A and B be their final positions such that AB = y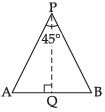
∠APB = 45° and they move with the same speed.
∴ ∠APB is an isosceles triangle. Draw 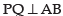
AB = y ∴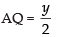 and PA = PB = x (let)
and PA = PB = x (let)
∠APQ = ∠BPQ =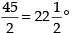
[∵ In an isosceles D, the altitude drawn from the vertex, bisects the base]
Now in right ΔAPQ ,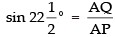
⇒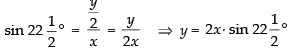
Differentiating both sides w.r.t, t, we get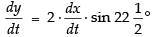
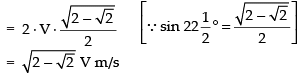
Hence, the rate of their separation is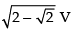 unit/s.
unit/s.
Q.5. Find an angle θ, 0 < θ <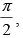 which increases twice as fast as its sine.
which increases twice as fast as its sine.
Ans.
As per the given condition,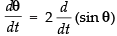
⇒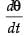 = 2 cos
= 2 cos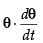 ⇒ 1 = 2 cos θ
⇒ 1 = 2 cos θ
∴ cos θ =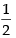 ⇒ cos θ =
⇒ cos θ =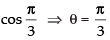
Hence, the required angle is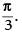
Q.6. Find the approximate value of (1.999)5.
Ans.
(1.999)5 = (2 – 0.001)5
Let x = 2 and Δx = – 0.001
Let y = x5
Differentiating both sides w.r.t, x, we get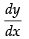 = 5x4 = 5(2)4= 80
= 5x4 = 5(2)4= 80
Now Δy =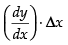 = 80 × (- 0.001) = - 0.080
= 80 × (- 0.001) = - 0.080
∴ (1.999)5 = y + Dy
= x5 – 0.080 = (2)5 – 0.080 = 32 – 0.080 = 31.92
Hence, approximate value of (1.999)5 is 31.92.
Q.7. Find the approximate volume of metal in a hollow spherical shell whose internal and external radii are 3 cm and 3.0005 cm, respectively.
Ans.
Internal radius r = 3 cm
and external radius R = r + Δr = 3.0005 cm
∴ Δr = 3.0005 – 3 = 0.0005 cm
Let y = r3 ⇒ y + Δy = (r + Δr)3 = R3 = (3.0005)3 ...(i)
Differentiating both sides w.r.t., r, we get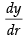 = 3r2
= 3r2
∴ Δy =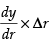 = 3r2 x 0.0005
= 3r2 x 0.0005
= 3 x (3)2 x 0.0005 = 27 x 0.0005 = 0.0135
∴ (3.0005)3 = y + Δy [From eq. (i)]
= (3)3 + 0.0135 = 27 + 0.0135 = 27.0135
Volume of the shell =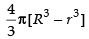
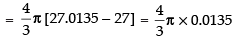
= 4π × 0.005 = 4 x 3.14 x 0.0045 = 0.018 π cm3
Hence, the approximate volume of the metal in the shell is 0.018 π cm3.
Q.8. A man, 2m tall, walks at the rate of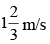 towards a street light which is
towards a street light which is 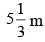 above the ground. At what rate is the tip of his shadow moving? At what rate is the length of the shadow changing when he is
above the ground. At what rate is the tip of his shadow moving? At what rate is the length of the shadow changing when he is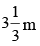 from the base of the light?
from the base of the light?
Ans.
Let AB is the height of street light post and CD is the height of the man such that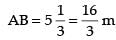 and CD 2 m
and CD 2 m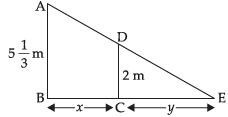
Let BC = x length (the distance of the man from the lamp post) and CE = y is the length of the shadow of the man at any instant.
From the figure, we see that
ΔABE ~ ΔDCE [by AAA Similarity]
∴ Taking ratio of their corresponding sides, we get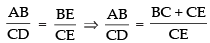
⇒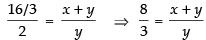
⇒ 8y = 3x + 3y ⇒ 8y - 3y = 3x ⇒ 5y = 3x
Differentiating both sides w.r.t, t, we get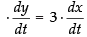
⇒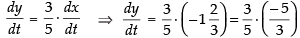
[∵ man is moving in opposite direction]
= - 1 m/s
Hence, the length of shadow is decreasing at the rate of 1 m/s.
Now let u = x + y
(u = distance of the tip of shadow from the light post)
Differentiating both sides w.r.t. t, we get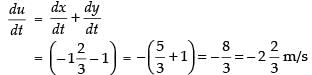
Hence, the tip of the shadow is moving at the rate of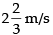
towards the light post and the length of shadow decreasing at the rate of 1 m/s.
Q.9. A swimming pool is to be drained for cleaning. If L represents the number of litres of water in the pool t seconds after the pool has been plugged off to drain and L = 200 (10 – t)2. How fast is the water running out at the end of 5 seconds? What is the average rate at which the water flows out during the first 5 seconds?
Ans.
Given that L = 200(10 – t)2
where L represents the number of litres of water in the pool.
Differentiating both sides w.r.t, t, we get∴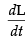 = 200 x 2(10 - t) (-1) = - 400(10 - t)
= 200 x 2(10 - t) (-1) = - 400(10 - t)
But the rate at which the water is running out
=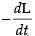 400(10 - t)...(1)
400(10 - t)...(1)
Rate at which the water is running after 5 seconds
= 400 x (10 - 5) = 2000 L/s (final rate)
For initial rate put t = 0 = 400(10 - 0) = 4000 L/s
The average rate at which the water is running out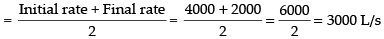
Hence, the required rate = 3000 L/s.
Q.10. The volume of a cube increases at a constant rate. Prove that the increase in its surface area varies inversely as the length of the side.
Ans.
Let x be the length of the cube
∴ Volume of the cube V = x3 ...(1)
Given that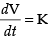
Differentiating Eq. (1) w.r.t. t, we get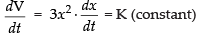
∴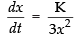
Now surface area of the cube, S = 6x2
Differentiating both sides w.r.t. t, we get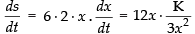
⇒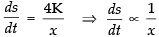 (4K = constant)
(4K = constant)
Hence, the surface area of the cube varies inversely as the length of the side.
Q.11. x and y are the sides of two squares such that y = x – x2 . Find the rate of change of the area of second square with respect to the area of first square.
Ans.
Let area of the first square A1 = x2
and area of the second square A2 = y2
Now A1= x2 and A2 = y2 = (x – x2)2
Differentiating both A1 and A2 w.r.t. t, we get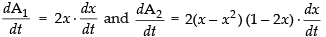
∴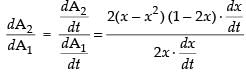
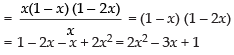
Hence, the rate of change of area of the second square with respect to first is
2x2 – 3x + 1.
Q.12. Find the condition that the curves 2x = y2 and 2xy = k intersect orthogonally.
Ans.
The two circles intersect orthogonally if the angle between the tangents drawn to the two circles at the point of their intersection is 90°.
Equation of the two circles are given as
2x = y2...(i)
and 2 = k ...(ii)
Differentiating eq. (i) and (ii) w.r.t. x, we get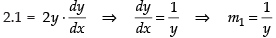
(m1 = slope of the tangent)
⇒ 2xy = k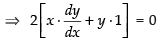
∴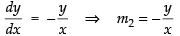
[m2 = slope of the other tangent]
If the two tangents are perpendicular to each other,
then m1 x m2 = – 1
⇒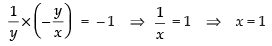
Now solving 2x = y2 [From (i)]
and 2xy = k [From (ii)]
From eq. (ii) 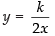
Putting the value of y in eq. (i)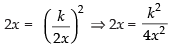
⇒ 8x3 = k2 ⇒ 8(1)3 = k2 ⇒ 8 = k2
Hence, the required condition is k2 = 8.
Q.13. Prove that the curves xy = 4 and x2 + y2 = 8 touch each other.
Ans.
Given circles are xy = 4 ...(i)
and x2 + y2 = 8 ...(ii)
Differentiating eq. (i) w.r.t., x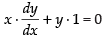
⇒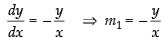 ...(iii)
...(iii)
where, m1 is the slope of the tangent to the curve.
Differentiating eq. (ii) w.r.t. x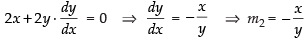
where, m2 is the slope of the tangent to the circle.
To find the point of contact of the two circles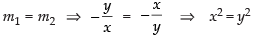
Putting the value of y2 in eq. (ii)
x2 + x2 = 8 ⇒ 2x2 = 8 ⇒ x2 = 4
∴ x = ± 2
∵ x2 = y2 ⇒ y = ± 2
∴ The point of contact of the two circles are (2, 2) and ( - 2, 2).
Q.14. Find the co-ordinates of the point on the curve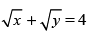 at which tangent is equally inclined to the axes.
at which tangent is equally inclined to the axes.
Ans.
Equation of curve is given by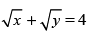
Let (x1, y1) be the required point on the curve
∴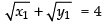
Differentiating both sides w.r.t. x1, we get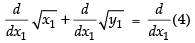
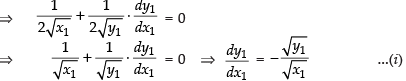
Since the tangent to the given curve at (x1, y1) is equally inclined to the axes.
∴ Slope of the tangent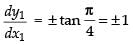
So, from eq. (i) we get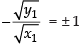
Squaring both sides, we get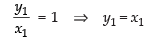
Putting the value of y1 in the given equation of the curve.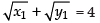
⇒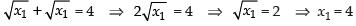
Since y1 = x1
∴ y1 = 4
Hence, the required point is (4, 4).
Q.15. Find the angle of intersection of the curves y = 4 – x2 and y = x2.
Ans.
We know that the angle of intersection of two curves is equal to the angle between the tangents drawn to the curves at their point of intersection.
The given curves are y = 4 – x2 ... (i) and y = x2 ...(ii)
Differentiating eq. (i) and (ii) with respect to x, we have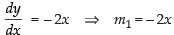
m1 is the slope of the tangent to the curve (i).
and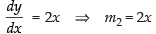
m2 is the slope of the tangent to the curve (ii).
So, m1 = – 2x and m2 = 2x
Now solving eq. (i) and (ii) we get
⇒ 4 – x2 = x2 ⇒ 2x2 = 4 ⇒ x2 = 2 ⇒ x = ± √2
So, m1 = - 2 x =- 2√2 and m2 = 2x = 2√2
Let θ be the angle of intersection of two curves
∴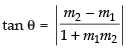
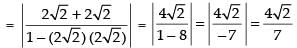
∴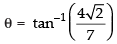
Hence, the required angle is tan-1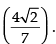
Q.16. Prove that the curves y2 = 4x and x2 + y2 – 6x + 1 = 0 touch each other at the point (1, 2).
Ans.
Given that the equation of the two curves are y2 = 4x ...(i)
and x2 + y2 – 6x + 1 = 0 ...(ii)
Differentiating (i) w.r.t. x, we get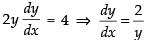
Slope of the tangent at (1, 2),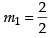 = 1
= 1
Differentiating (ii) w.r.t. x ⇒ 2x + 2y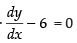
⇒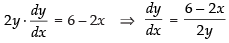
∴ Slope of the tangent at the same point (1, 2)
⇒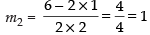
We see that m1 = m2 = 1 at the point (1, 2).
Hence, the given circles touch each other at the same point (1, 2).
Q.17. Find the equation of the normal lines to the curve 3x2 – y2 = 8 which are parallel to the line x + 3y = 4.
Ans.
We have equation of the curve 3x2 – y2 = 8
Differentiating both sides w.r.t. x, we get
⇒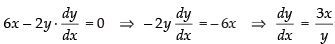
Slope of the tangent to the given curve =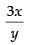
∴ Slope of the normal to the curve =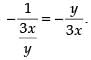
Now differentiating both sides the given line x + 3y = 4
⇒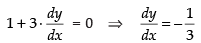
Since the normal to the curve is parallel to the given line x + 3y = 4.
∴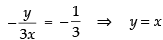
Putting the value of y in 3x2 – y2 = 8, we get
3x2 – x2 = 8 ⇒ 2x2 = 8 ⇒ x2 = 4 ⇒ x = ± 2
∴ y = ± 2
∴ The points on the curve are (2, 2) and (– 2, – 2).
Now equation of the normal to the curve at (2, 2) is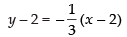
⇒ 3y – 6 = – x + 2 ⇒ x + 3y = 8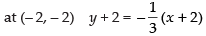
⇒ 3y + 6 = – x – 2 ⇒ x + 3y = – 8
Hence, the required equations are x + 3y = 8 and x + 3y = – 8 or x + 3y = ± 8.
Q.18. At what points on the curve x2 + y2 – 2x – 4y + 1 = 0, the tangents are parallel to the y-axis?
Ans.
Given that the equation of the curve is
x2 + y2 – 2x – 4y + 1 = 0 ...(i)
Differentiating both sides w.r.t. x, we have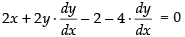
⇒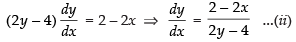
Since the tangent to the curve is parallel to the y-axis.
∴ Slope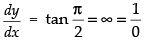
So, from eq. (ii) we get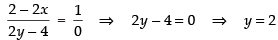
Now putting the value of y in eq. (i), we get
⇒ x2 + (2)2 – 2x – 8 + 1 = 0
⇒ x2 – 2x + 4 – 8 + 1 = 0
⇒ x2 – 2x – 3 = 0 ⇒ x2 – 3x + x – 3 = 0
⇒ x(x – 3) + 1(x – 3) = 0 ⇒ (x - 3) (x + 1) = 0
⇒ x = – 1 or 3
Hence, the required points are (– 1, 2) and (3, 2).
Q.19. Show that the line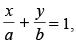 touches the curve y = b.
touches the curve y = b.
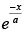 at the point where the curve intersects the axis of y.
at the point where the curve intersects the axis of y.
Ans.
Given that y = b × e– x/a, the equation of curve
and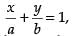 the equation of line.
the equation of line.
Let the coordinates of the point where the curve intersects the y-axis be (0, y1) Now differentiating y = b × e– x/a both sides w.r.t. x, we get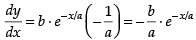
So, the slope of the tangent, m1 =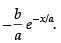
Differentiating 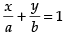 both sides w.r.t. x, we get
both sides w.r.t. x, we get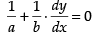
So, the slope of the line, m2 =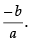
If the line touches the curve, then m1 = m2
⇒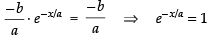
⇒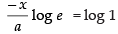 (Taking log on both sides)
(Taking log on both sides)
⇒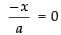 ⇒ x = 0
⇒ x = 0
Putting x = 0 in equation y = b × e – x/a
⇒ y = b × e0 = b
Hence, the given equation of curve intersect at (0, b) i.e. on y-axis.
Q.20. Show that f (x) = 2x + cot–1x + log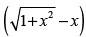 is increasing in R.
is increasing in R.
Ans.
Given that f (x) = 2x + cot–1x + log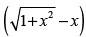
Differentiating both sides w.r.t. x, we get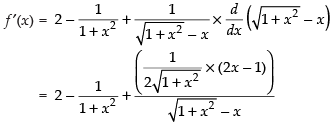
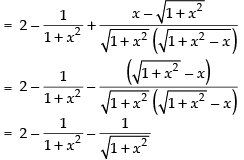
For increasing function, f ′(x) ≠ 0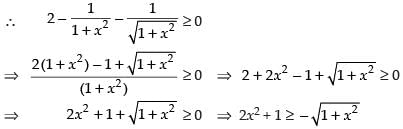 ⇒
⇒
Squaring both sides, we get 4x4 + 1 + 4x2 ≥ 1 + x2
⇒ 4x4 + 4x2 - x2 ≥ 0 ⇒ 4x4 + 3x2 ≥ 0 ⇒ x2(4x2 + 3) ≠ 0
which is true for any value of x ∈ R.
Hence, the given function is an increasing function over R.
Q.21. Show that for a ≥ 1, f (x) = √3 sinx – cosx – 2ax + b is decreasing in R.
Ans.
Given that: f (x) = √3 sin x - cos x - 2ax + b, a≥ 1
Differentiating both sides w.r.t. x, we get
f ′(x) = √3 cos x + sin x- 2a
For decreasing function, f ′(x) < 0
∴ √3 cos x + sin x- 2a < 0
⇒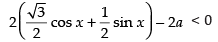
⇒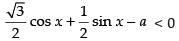
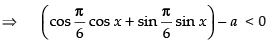
⇒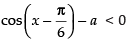
Since cos x ∈ [ - 1, 1] and a ≥ 1
∴ f ′(x) < 0
Hence, the given function is decreasing in R.
Q.22. Show that f (x) = tan–1(sinx + cosx) is an increasing function in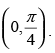
Ans.
Given that: f (x) = tan–1(sin x + cos x) in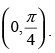
Differentiating both sides w.r.t. x, we get 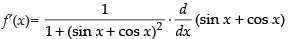
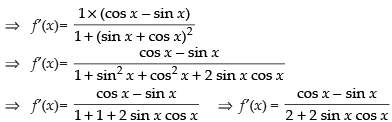
For an increasing function f ′(x) ≥ 0
∴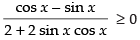
⇒ cos x – sin x ≥ 0 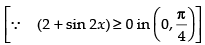
⇒ cos x ≥ sin x, which is true for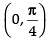
Hence, the given function f(x) is an increasing function in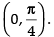
Q.23. At what point, the slope of the curve y = – x3 + 3x2 + 9x – 27 is maximum? Also find the maximum slope.
Ans.
Given that: y = – x3 + 3x2 + 9x – 27
Differentiating both sides w.r.t. x, we get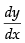 = – 3x2 + 6x + 9
= – 3x2 + 6x + 9
Let slope of the curve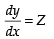
∴ z = -3x2 + 6x + 9
Differentiating both sides w.r.t. x, we get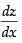 = – 6x + 6
= – 6x + 6
For local maxima and local minima,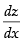 = 0
= 0
∴ – 6x + 6 = 0 ⇒ x = 1
⇒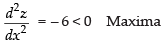
Put x = 1 in equation of the curve y = (– 1)3 + 3(1)2 + 9(1) – 27
= – 1 + 3 + 9 – 27 = – 16
Maximum slope = – 3(1)2 + 6(1) + 9 = 12
Hence, (1, – 16) is the point at which the
slope of the given curve is maximum and maximum slope = 12.
Q.24. Prove that f (x) = sinx + √3 cosx has maximum value at x =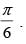
Ans.
We have: f (x) = sin x + √3 cosx =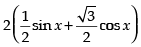
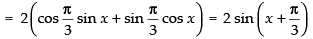
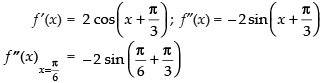
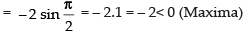
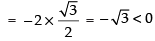 (Maxima)
(Maxima)
Maximum value of the function at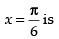
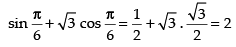
Hence, the given function has maximum value at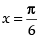 and the maximum value is 2.
and the maximum value is 2.
Long Answer (L.A.)
Q.25. If the sum of the lengths of the hypotenuse and a side of a right angled triangle is given, show that the area of the triangle is maximum when the angle between them is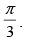
Ans.
Let ΔABC be the right angled triangle in which ∠B = 90°
Let AC = x, BC = y
∴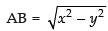
∠ACB = θ
Let Z = x + y (given)
Now area of ΔABC,A =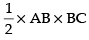
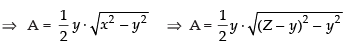
Squaring both sides, we get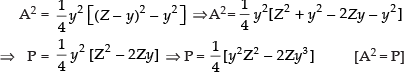
Differentiating both sides w.r.t. y we get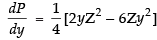 ...(i)
...(i)
For local maxima and local minima,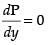
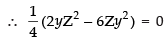
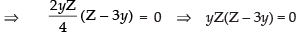
⇒ yZ ≠ 0 ( ∵ y ≠ 0 and Z ≠ 0)
∴ Z - 3y = 0
⇒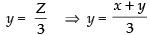 ( ∵ Z = x + y)
( ∵ Z = x + y)
⇒ 3y = x + y ⇒ 3y - y = x ⇒ 2y = x
⇒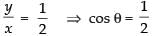
∴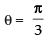
Differentiating eq. (i) w.r.t. y, we have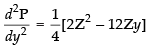
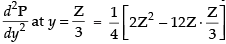
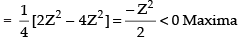
Hence, the area of the given triangle is maximum when the angle
between its hypotenuse and a side is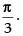
Q.26. Find the points of local maxima, local minima and the points of inflection of the function f (x) = x5 – 5x4 + 5x3 – 1. Also find the corresponding local maximum and local minimum values.
Ans.
We have f (x) = x5 – 5x4 + 5x3 – 1
⇒ f ′(x) = 5x4 - 20x3 + 15x2
For local maxima and local minima, f ′(x) = 0
⇒ 5x4 – 20x3 + 15x2 = 0 ⇒ 5x2(x2 - 4x + 3) = 0
⇒ 5x2(x2 - 3x - x + 3) = 0 ⇒ x2(x - 3) (x - 1) = 0
∴ x = 0, x = 1 and x = 3
Now f ″(x) = 20x3 - 60x2 + 30x
⇒ f ″(x)at x = 0 = 20(0)3 - 60(0)2 + 30(0) = 0 which is neither maxima nor minima.
∴ f (x) has the point of inflection at x = 0
f ″(x)at x = 1 = 20(1)3 - 60(1)2 + 30(1)
= 20 - 60 + 30 = - 10 < 0 Maxima
f ″(x)at x = 3 = 20(3)3 - 60(3)2 + 30(3)
= 540 - 540 + 90 = 90 > 0 Minima
The maximum value of the function at x = 1
f(x) = (1)5 – 5(1)4 + 5(1)3 – 1 = 1 – 5 + 5 – 1 = 0
The minimum value at x = 3 is
f (x) = (3)5 – 5(3)4 + 5(3)3 – 1
= 243 – 405 + 135 – 1 = 378 – 406 = – 28
Hence, the function has its maxima at x = 1 and the maximum value = 0 and it has minimum value at x = 3 and its minimum value is – 28.
x = 0 is the point of inflection.
Q.27. A telephone company in a town has 500 subscribers on its list and collects fixed charges of ₹ 300/- per subscriber per year. The company proposes to increase the annual subscription and it is believed that for every increase of ₹ 1/- one subscriber will discontinue the service. Find what increase will bring maximum profit?
Ans.
Let us consider that the company increases the annual subscription by ₹ x.
So, x is the number of subscribers who discontinue the services.
∴ Total revenue, R(x) = (500 – x) (300 + x)
= 150000 + 500x – 300x – x2
= – x2 + 200x + 150000
Differentiating both sides w.r.t. x, we get R ′(x) = - 2x + 200
For local maxima and local minima, R ′(x) = 0
- 2x + 200 = 0 ⇒ x = 100
R ″(x) = - 2 < 0 Maxima
So, R(x) is maximum at x = 100
Hence, in order to get maximum profit, the company should increase its annual subscription by ₹ 100.
Q.28. If the straight line x cosα + y sinα = p touches the curve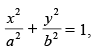 then prove that a2 cos2α + b2 sin2α = p2.
then prove that a2 cos2α + b2 sin2α = p2.
Ans.
The given curve is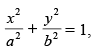 ...(i)
...(i)
and the straight line x cos α + y sin α = p ...(ii)
Differentiating eq. (i) w.r.t. x, we get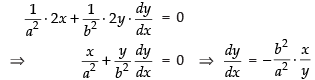
So the slope of the curve =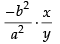
Now differentiating eq. (ii) w.r.t. x, we have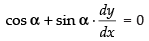
∴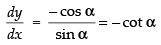
So, the slope of the straight line = – cot α
If the line is the tangent to the curve, then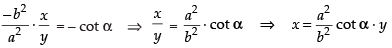
Now from eq. (ii) we have x cos α + y sin α = p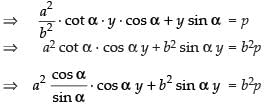
⇒ a2 cos2 αy + b2 sin2 αy = b2 sin αp
⇒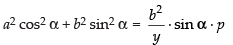
⇒ a2 cos2 α + b2 sin2 α = p × p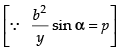
Hence, a2 cos2 α + b2 sin2 α = p2
Alternate method:
We know that y = mx + c will touch the ellipse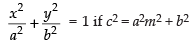
Here equation of straight line is x cos α + y sin α = p and
that of ellipse is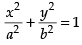
x cos α + y sin α = p
⇒ y sin α = – x cos α + p
⇒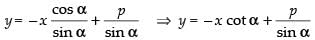
Comparing with y = mx + c, we get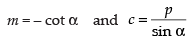
So, according to the condition, we get c2 = a2m2 + b2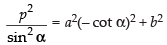
⇒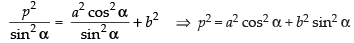
Hence, a2 cos2 α + b2 sin2 α = p2
Hence proved.
Q.29. An open box with square base is to be made of a given quantity of card board of area c2. Show that the maximum volume of the box is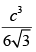 cubic units.
cubic units.
Ans.
Let x be the length of the side of the square base of the cubical open box and y be its height.
∴ Surface area of the open box
c2 = x2 + 4xy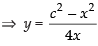 ...(i)
...(i)
Now volume of the box, V = x x x x y
⇒ V = x2y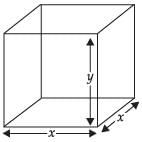
Differentiating both sides w.r.t. x, we get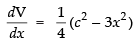 ...(ii)
...(ii)
For local maxima and local minima,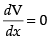
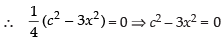
⇒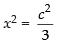
∴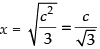
Now again differentiating eq. (ii) w.r.t. x, we get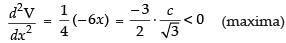
Volume of the cubical box (V) = x2 y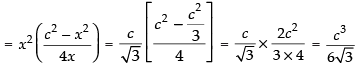
Hence, the maximum volume of the open box is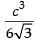 cubic units.
cubic units.
Q.30. Find the dimensions of the rectangle of perimeter 36 cm which will sweep out a volume as large as possible, when revolved about one of its sides. Also find the maximum volume.
Ans.
Let x and y be the length and breadth of a given rectangle ABCD as per question, the rectangle be revolved about side AD which will make a cylinder with radius x and height y.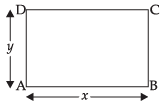
∴ Volume of the cylinder V = πr2h
⇒ V = πx2y ...(i)
Now perimeter of rectangle P = 2(x + y) ⇒ 36 = 2(x + y)
⇒ x + y = 18 ⇒ y = 18 – x ...(ii)
Putting the value of y in eq. (i) we get
V = πx2(18 – x)
⇒ V = π(18x2 – x3)
Differentiating both sides w.r.t. x, we get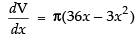 ...(iii)
...(iii)
For local maxima and local minima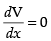
∴ p(36x – 3x2) = 0 ⇒ 36x – 3x2 = 0
⇒ 3x(12 – x) = 0
⇒ x ≠ 0 ∴ 12 – x = 0 ⇒ x = 12
From eq. (ii) y = 18 – 12 = 6
Differentiating eq. (iii) w.r.t. x, we get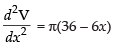
at x = 12 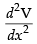 = π(36 – 6 x 12)
= π(36 – 6 x 12)
= π(36 - 72) = - 36π < 0 maxima
Now volume of the cylinder so formed = πx2y
= π x (12)2 x 6 = π x 144 x 6 = 864π cm3
Hence, the required dimensions are 12 cm and 6 cm and the maximum volume is 864π cm3.
Q.31. If the sum of the surface areas of cube and a sphere is constant, what is the ratio of an edge of the cube to the diameter of the sphere, when the sum of their volumes is minimum?
Ans.
Let x be the edge of the cube and r be the radius of the sphere.
Surface area of cube = 6x2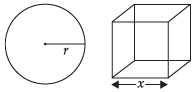
and surface area of the sphere = 4πr2
∴ 6x2 + 4πr2 = K(constant) ⇒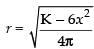 ...(i)
...(i)
Volume of the cube = x3 and the volume of sphere =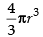
∴ Sum of their volumes (V) = Volume of cube + Volume of sphere
⇒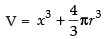
⇒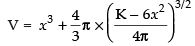
Differentiating both sides w.r.t. x, we get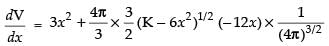
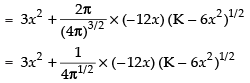
∴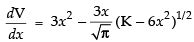 ...(ii)
...(ii)
For local maxima and local minima,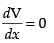
∴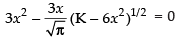
⇒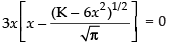
x ≠ 0 ∴ x -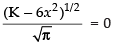
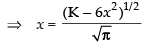
Squaring both sides, we get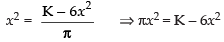
⇒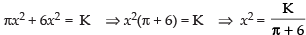
∴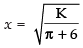
Now putting the value of K in eq. (i), we get
6x2 + 4πr2 = x2(p + 6)
⇒ 6x2 + 4πr2 = πx2 + 6x2 ⇒ 4πr2 = πx2 ⇒ 4r2 = x2
∴2r = x
∴ x : 2r = 1 : 1
Now differentiating eq. (ii) w.r.t x, we have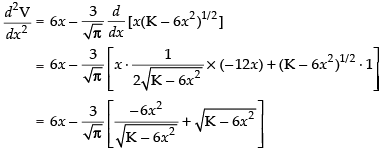
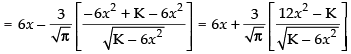
Put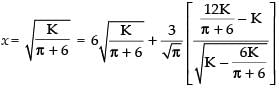

So it is minima.
Hence, the required ratio is 1 : 1 when the combined volume is minimum.
Q.32. AB is a diameter of a circle and C is any point on the circle. Show that the area of ∆ ABC is maximum, when it is isosceles.
Ans.
Let AB be the diameter and C be any point on the circle with radius r.
∠ACB = 90° [angle in the semi circle is 90°]
Let AC = x
∴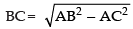
⇒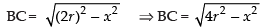 ...(i)
...(i)
Now area of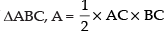
⇒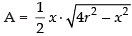
Squaring both sides, we get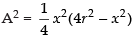
Let A2 = Z
∴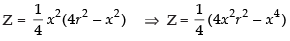
Differentiating both sides w.r.t. x, we get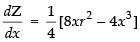 ...(ii)
...(ii)
For local maxima and local minima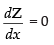
∴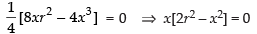
x ≠ 0 ∴ 2r2 - x2 = 0
⇒ x2 = 2r2 ⇒ x = √2r = AC
Now from eq. (i) we have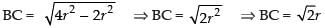
So AC = BC
Hence, ΔABC is an isosceles triangle.
Differentiating eq. (ii) w.r.t. x, we get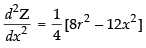
Put x = √2r
∴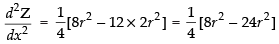
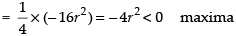
Hence, the area of ΔABC is maximum when it is an isosceles triangle.
Q.33. A metal box with a square base and vertical sides is to contain 1024 cm3. The material for the top and bottom costs Rs 5/cm2 and the material for the sides costs Rs 2.50/cm2 . Find the least cost of the box.
Ans.
Let x be the side of the square base and y be the length of the vertical sides.
Area of the base and bottom = 2x2 cm2
∴Cost of the material required = ₹ 5 x 2x2 = ₹ 10x2
Area of the 4 sides = 4xy cm2
∴ Cost of the material for the four sides
= ₹ 2.50 x 4xy = ₹ 10xy
Total cost C = 10x2 + 10xy ...(i)
New volume of the box = x x x x y
⇒ 1024 = x2y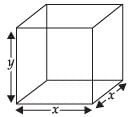
∴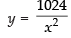 ...(ii)
...(ii)
Putting the value of y in eq. (i) we get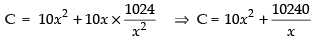
Differentiating both sides w.r.t. x, we get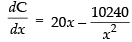 ...(iii)
...(iii)
For local maxima and local minima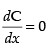
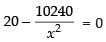
⇒ 20x3 – 10240 = 0 ⇒ x3 = 512 ⇒ x = 8 cm
Now from eq. (ii)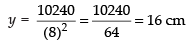
∴ Cost of material used C = 10x2 + 10xy
= 10 x 8 x 8 + 10 x 8 x 16 = 640 + 1280 = 1920
Now differentiating eq. (iii) we get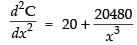
Put x = 8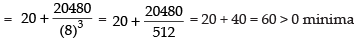
Hence, the required cost is ₹1920 which is the minimum.
Q.34. The sum of the surface areas of a rectangular parallelopiped with sides x, 2x and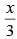 and a sphere is given to be constant. Prove that the sum of their volumes is minimum, if x is equal to three times the radius of the sphere. Also find the minimum value of the sum of their volumes.
and a sphere is given to be constant. Prove that the sum of their volumes is minimum, if x is equal to three times the radius of the sphere. Also find the minimum value of the sum of their volumes.
Ans.
Let ‘r ’ be the radius of the sphere.
∴ Surface area of the sphere = 4πr2
Volume of the sphere =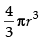
The sides of the parallelopiped are x, 2x and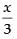
∴ Its surface area =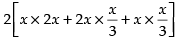
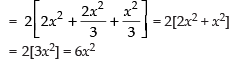
Volume of the parallelopiped =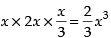
As per the conditions of the question,
Surface area of the parallelopiped + Surface area of the sphere = constant
⇒ 6x2 + 4πr2 = K (constant) ⇒ 4πr2 = K - 6x2
∴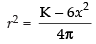 ...(i)
...(i)
Now let V = Volume of parallelopiped + Volume of the sphere
⇒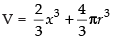
⇒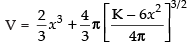 [from eq. (i)]
[from eq. (i)]
⇒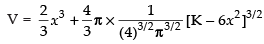
⇒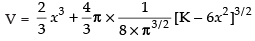
⇒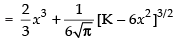
Differentiating both sides w.r.t. x, we have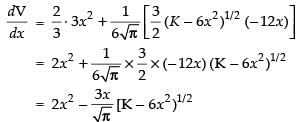
For local maxima and local minima, we have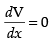
∴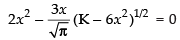
⇒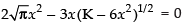
⇒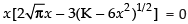
Here x ≠ 0 and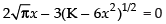
⇒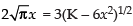
Squaring both sides, we get
4πx2 = 9(K – 6x2) ⇒ 4πx2 = 9K - 54x2
⇒ 4πx2 + 54x2 = 9K
⇒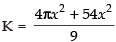 ...(ii)
...(ii)
⇒ 2x2(2π + 27) = 9K
∴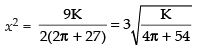
Now from eq. (i) we have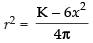
⇒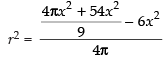
⇒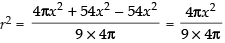
⇒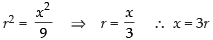
Now we have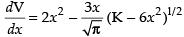
Differentiating both sides w.r.t. x, we get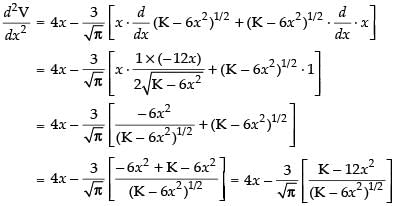
Put 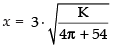
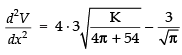
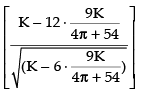
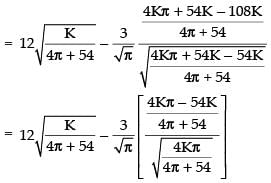

[ ∵ 27 - 2π > 0]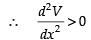 so, it is minima.
so, it is minima.
Hence, the sum of volume is minimum for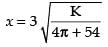
∴ Minimum volume,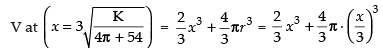
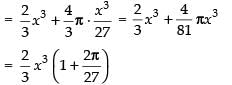
Hence, the required minimum volume is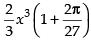 and x = 3r.
and x = 3r.
|
177 videos|618 docs|160 tests
|
FAQs on NCERT Exemplar: Application of Derivatives- 1 - Mathematics (Maths) for JEE Main & Advanced
| 1. What is the concept of derivatives in mathematics? |  |
| 2. How are derivatives applied in real-life situations? |  |
| 3. What are the different rules for finding derivatives? |  |
| 4. How can derivatives be used to optimize functions? |  |
| 5. Can derivatives be used to approximate functions? |  |





















