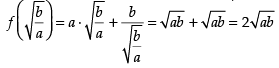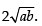Objective Type Questions
Q.35. The sides of an equilateral triangle are increasing at the rate of 2 cm/sec. The rate at which the area increases, when side is 10 cm is:
(a) 10 cm2/s
(b) √3 cm2/s
(c) 10 √3 cm2/s
(d) 10/3 cm2/s
Ans. (c)
Solution.
Let the length of each side of the given equilateral triangle be x cm.
∴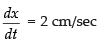
Area of equilateral triangle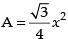
∴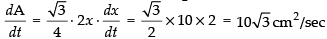
Hence, the rate of increasing of area = 10 √3 cm2/sec .
Hence, the correct option is (c).
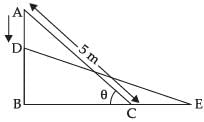
Q.36. A ladder, 5 meter long, standing on a horizontal floor, leans against a vertical wall. If the top of the ladder slides downwards at the rate of 10 cm/sec, then the rate at which the angle between the floor and the ladder is decreasing when lower end of ladder is 2 metres from the wall is:
(a) 1/10 radian/sec
(b) 1/20 radian/sec
(c) 20 radian/sec
(d) 10 radian/sec
Ans. (b)
Solution.
Length of ladder = 5 m
Let AB = y m and BC = x m
∴ In right ΔABC,
AB2 + BC2 = AC2
⇒ x2 + y2 = (5)2 ⇒ x2 + y2 = 25
Differentiating both sides w.r.t x, we have
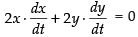
⇒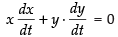
⇒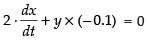 [∵ x = 2m]
[∵ x = 2m]
⇒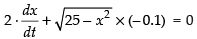
⇒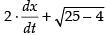 x (- 0.1) = 0
x (- 0.1) = 0
⇒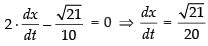
Now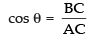 (θ is in radian)
(θ is in radian)
⇒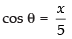
Differentiating both sides w.r.t. t, we get
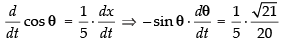
⇒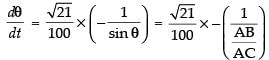
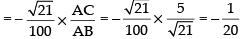 radian/sec
radian/sec
[(–) sign shows the decrease of change of angle]
Hence, the required rate =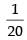 radian/sec
radian/sec
Hence, the correct option is (b).
Q.37. The curve y =x1/5 has at (0, 0)
(a) a vertical tangent (parallel to y-axis)
(b) a horizontal tangent (parallel to x-axis)
(c) an oblique tangent
(d) no tangent
Ans. (a)
Solution.
Equation of curve is y = x1/5
Differentiating w.r.t. x, we get 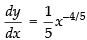
(at x = 0)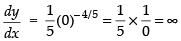
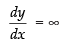
∴ The tangent is parallel to y-axis.
Hence, the correct option is (a).
Q.38. The equation of normal to the curve 3x2 – y2 = 8 which is parallel to the line x + 3y = 8 is
(a) 3x – y = 8
(b) 3x + y + 8 = 0
(c) x + 3y ± 8 = 0
(d) x + 3y = 0
Ans. (c)
Solution.
Given equation of the curve is 3x2 – y2 = 8 ...(i)
Differentiating both sides w.r.t. x, we get
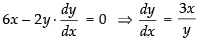
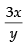 is the slope of the tangent
is the slope of the tangent
∴ Slope of the normal =
Now x + 3y = 8 is parallel to the normal
Differentiating both sides w.r.t. x, we have

∴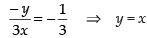
Putting y = x in eq. (i) we get
3x2 – x2 = 8 ⇒ 2x2 = 8 ⇒ x2 = 4
∴ x = ± 2 and y = ± 2
So the points are (2, 2) and (– 2, – 2).
Equation of normal to the given curve at (2, 2) is
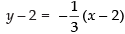
⇒ 3y – 6 = – x + 2 ⇒ x + 3y – 8 = 0
Equation of normal at (– 2, – 2) is
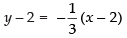
⇒ 3y + 6 = – x – 2 ⇒ x + 3y + 8 = 0
∴ The equations of the normals to the curve are
x + 3y ± 8 = 0
Hence, the correct option is (c).
Q.39. If the curve ay + x2 = 7 and x3 = y, cut orthogonally at (1, 1), then the value of a is:
(a) 1
(b) 0
(c) – 6
(d) 6
Ans. (d)
Solution.
Equation of the given curves are ay + x2 = 7 ...(i)
and x3 = y ...(ii)
Differentiating eq. (i) w.r.t. x, we have
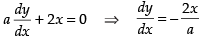
∴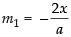
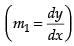
Now differentiating eq. (ii) w.r.t. x, we get
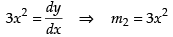
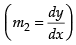
The two curves are said to be orthogonal if the angle between the tangents at the point of intersection is 90°.
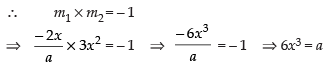
(1, 1) is the point of intersection of two curves.
∴ 6(1)3 = a
So a = 6
Hence, the correct option is (d).
Q.40. If y = x4 – 10 and if x changes from 2 to 1.99, what is the change in y
(a) 0.32
(b) 0.032
(c) 5.68
(d) 5.968
Ans. (a)
Solution.
Given that y = x4 – 10
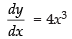
Δx = 2.00 – 1.99 = 0.01
∴
= 4 x (2)3 x 0.01 = 32 x 0.01 = 0.32
Hence, the correct option is (a).
Q.41. The equation of tangent to the curve y (1 + x2) = 2 – x, where it crosses x-axis is:
(a) x + 5y = 2
(b) x – 5y = 2
(c) 5x – y = 2
(d) 5x + y = 2
Ans. (a)
Solution.
Given that y(1 + x2) = 2 – x ...(i)
If it cuts x-axis, then y-coordinate is 0.
∴ 0(1 + x2) = 2 – x ⇒ x = 2
Put x = 2 in equation (i)
y(1 + 4) = 2 – 2 ⇒ y(5) = 0 ⇒ y = 0
Point of contact = (2, 0)
Differentiating eq. (i) w.r.t. x, we have
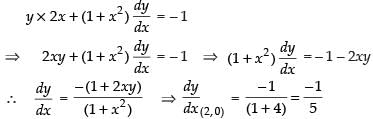
Equation of tangent is y – 0 =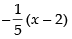
⇒ 5y = – x + 2 ⇒ x + 5y = 2
Hence, the correct option is (a).
Q.42. The points at which the tangents to the curve y = x3 – 12x + 18 are parallel to x-axis are:
(A) (2, –2), (–2, –34)
(B) (2, 34), (–2, 0)
(C) (0, 34), (–2, 0)
(D) (2, 2), (–2, 34)
Ans. (d)
Solution.
Given that y = x3 – 12x + 18
Differentiating both sides w.r.t. x, we have
⇒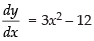
Since the tangents are parallel to x-axis, then
∴ 3x2 – 12 = 0 ⇒ x = ± 2
∴ yx=2 = (2)3 – 12(2) + 18 = 8 – 24 + 18 = 2
yx=–2 = (– 2)3 – 12(– 2) + 18 = – 8 + 24 + 18 = 34
∴ Points are (2, 2) and (– 2, 34)
Hence, the correct option is (d).
Q.43. The tangent to the curve y = e2x at the point (0, 1) meets x-axis at:
(a) (0, 1)
(b)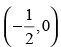
(c) (2, 0)
(d) (0, 2)
Ans. (b)
Solution.
Equation of the curve is y = e2x
Slope of the tangent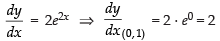
∴ Equation of tangent to the curve at (0, 1) is
y –1 = 2(x – 0)
⇒ y – 1 = 2x ⇒ y – 2x = 1
Since the tangent meets x-axis where y = 0
∴ 0 – 2x = 1 ⇒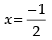
So the point is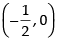
Hence, the correct option is (b).
Q.44. The slope of tangent to the curve x = t2 + 3t – 8, y = 2t2 – 2t – 5 at the point (2, –1) is:
(a) 22/ 7
(b) 6/7
(c) - 6/7
(d) – 6
Ans. (b)
Solution.
The given curve is x = t2 + 3t – 8 and y = 2t2 – 2t – 5

∴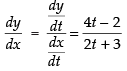
Now (2, – 1) lies on the curve
⇒ 2 = t2 + 3t – 8 ⇒ t2 + 3t – 10 = 0
⇒ t2 + 5t –2t – 10 = 0
⇒ t(t + 5) – 2(t + 5) = 0
⇒ (t + 5) (t – 2) = 0
∴ t = 2, t = – 5 and – 1 = 2t2 – 2t – 5
⇒ 2t2 – 2t – 4 = 0
⇒ t2 – t – 2 = 0 ⇒ t2 – 2t + t – 2 = 0
⇒ t(t – 2) + 1 (t – 2) = 0 ⇒ (t + 1) (t - 2) = 0
⇒ t = – 1 and t = 2
So t = 2 is common value
∴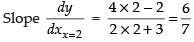
Hence, the correct option is (b).
Q.45. The two curves x3 – 3xy2 + 2 = 0 and 3x2y – y3 – 2 = 0 intersect at an angle of
(a) π/4
(b) π/3
(c) π/2
(d) π/6
Ans. (c)
Solution.
The given curves are x3 – 3xy2 + 2 = 0 ...(i)
and 3x2y – y3 – 2 = 0 ...(ii)
Differentiating eq. (i) w.r.t. x, we get
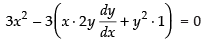
⇒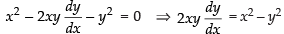
∴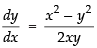
So slope of the curve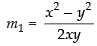
Differentiating eq. (ii) w.r.t. x, we get

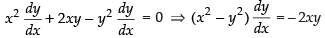
∴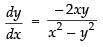
So the slope of the curve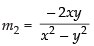
Now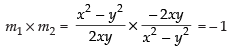
So the angle between the curves is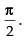
Hence, the correct option is (c).
Q.46. The interval on which the function f (x) = 2x3 + 9x2 + 12x – 1 is decreasing is:
(a) [–1, ∞ )
(b) [–2, –1]
(c) (– ∞ , –2]
(d) [–1, 1]
Ans. (b)
Solution.
The given function is f (x) = 2x3 + 9x2 + 12x - 1
f ′(x) = 6x2 + 18x + 12
For increasing and decreasing f ′(x) = 0
∴ 6x2 + 18x + 12 = 0
⇒ x2 + 3x + 2 = 0 ⇒ x2 + 2x + x + 2 = 0
⇒ x(x + 2) + 1(x + 2) = 0 ⇒ (x + 2) (x + 1) = 0
⇒ x = – 2, x = – 1
The possible intervals are (–∞, - 2), ( - 2, - 1), ( - 1, ∞)
Now f ′(x) = (x + 2) (x + 1)
⇒ f ′(x)( - ∞, - 2) = (-) (-) = (+) increasing
⇒ f ′(x)(- 2, - 1) = (+) (-) = (-) decreasing
⇒ f ′(x)(- 1, ∞) = (+) (+) = (+) increasing
Hence, the correct option is (b).
Q.47. Let the f : R → R be defined by f (x) = 2x + cosx, then f :
(a) has a minimum at x = π
(b) has a maximum, at x = 0
(c) is a decreasing function
(d) is an increasing function
Ans. (d)
Solution.
Given that f (x) = 2x + cos x
f ′(x) = 2 - sin x
Since f ′(x) > 0 ∀ x
So f (x) is a n increasing function.
Hence, the correct option is (d).
Q.48. y = x (x – 3)2 decreases for the values of x given by :
(a) 1 < x < 3
(b) x < 0
(c) x > 0
(d) 0 < x < 3/2
Ans. (a)
Solution.
Here y = x(x – 3)2
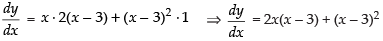
For increasing and decreasing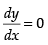
∴ 2x(x – 3) + (x – 3)2 = 0 ⇒ (x - 3) (2x + x - 3) = 0
⇒ (x – 3) (3x – 3) = 0 ⇒ 3(x - 3) (x - 1) = 0
∴ x = 1, 3
∴ Possible intervals are (– ∞, 1), (1, 3), (3, ∞)
dy/dx = (x - 3) (x - 1)
For (- ∞ , 1) =(-) (-) = (+) increasing
For (1, 3) =(-) (+) = (-) decreasing
For (3, ∞) =(+) (+) = (+) increasing
So the function decreases in (1, 3) or 1 < x < 3
Hence, the correct option is (a).
Q.49. The function f (x) = 4 sin3x – 6 sin2x + 12 sinx + 100 is strictly
(a) increasing in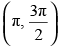
(b) decreasing in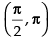
(c) decreasing in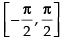
(d) decreasing in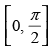
Ans. (b)
Solution.
Here,
f (x) = 4 sin3 x – 6 sin2 x + 12 sin x + 100
f ′(x) = 12 sin2 x × cos x - 12 sin x cos x + 12 cos x
= 12 cos x [sin2 x - sin x + 1]
= 12 cos x [sin2 x + (1 - sin x)]
∴ 1 - sin x ≥ 0 and sin2 x ≥ 0
∴ sin2 x + 1 - sin x ≥ 0 (when cos x > 0)
Hence, f ′(x) > 0 , when cos x > 0 i.e.,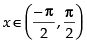
So, f(x) is in creasing where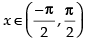 and f ′(x) < 0
and f ′(x) < 0
when cos x < 0 i.e.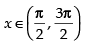
Hence, (x) is decreasing when
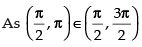
So f(x) is decreasing in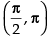
Hence, the correct option is (b).
Q.50. Which of the following functions is decreasing on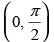
(a) sin 2x
(b) tan x
(c) cos x
(d) cos 3x
Ans. (c)
Solution.
Here, Let f (x) = cos x; So, f ′(x) = - sin x
f ′(x) < 0 in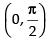
So f (x) = cos x is decreasing in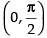
Hence, the correct option is (c).
Q.51. The function f (x) = tanx – x
(a) always increases
(b) always decreases
(c) never increases
(d) sometimes increases and sometimes decreases.
Ans. (a)
Solution.
Here, f(x) = tan x – x So, f ′(x) = sec2 x - 1
f ′(x) > 0 ∀ x ∈ R
So f (x) is always increasing
Hence, the correct option is (a).
Q.52. If x is real, the minimum value of x2 – 8x + 17 is
(a) – 1
(b) 0
(c) 1
(d) 2
Ans. (c)
Solution.
Let f (x) = x2 – 8x + 17
f ′(x) = 2x - 8
For local maxima and local minima, f ′(x) = 0
∴ 2x – 8 = 0 ⇒ x = 4
So, x = 4 is the point of local maxima and local minima.
f ″(x) = 2 > 0 minima at x = 4
∴ f(x)x=4 = (4)2 – 8(4) + 17
= 16 – 32 + 17 = 33 – 32 = 1
So the minimum value of the function is 1
Hence, the correct option is (c).
Q.53. The smallest value of the polynomial x3 – 18x2 + 96x in [0, 9] is
(a) 126
(b) 0
(c) 135
(d) 160
Ans. (b)
Solution.
Let f(x) = x3 – 18x2 + 96x; So, f ′(x) = 3x2 - 36x + 96
For local maxima and local minima f ′(x) = 0
∴ 3x2 - 36x + 96 = 0
⇒ x2 - 12x + 32 = 0 ⇒ x2 - 8x - 4x + 32 = 0
⇒ x(x - 8) - 4(x - 8) = 0 ⇒ (x - 8) (x - 4) = 0
∴ x = 8, 4 ∈ [0, 9]
So, x = 4, 8 are the points of local maxima and local minima.
Now we will calculate the absolute maxima or absolute
minima at x = 0, 4, 8, 9
∴ f(x) = x3 – 18x2 + 96x
f(x)x=0 = 0 – 0 + 0 = 0
f(x)x=4 = (4)3 – 18(4)2 + 96(4)
= 64 – 288 + 384 = 448 – 288 = 160
f(x)x=8 = (8)3 – 18(8)2 + 96(8)
= 512 – 1152 + 768 = 1280 – 1152 = 128
f(x)x=9 = (9)3 – 18(9)2 + 96(9)
= 729 – 1458 + 864 = 1593 – 1458 = 135
So, the absolute minimum value of f is 0 at x = 0
Hence, the correct option is (b).
Q.54. The function f (x) = 2x3 – 3x2 – 12x + 4, has
(a) two points of local maximum
(b) two points of local minimum
(c) one maxima and one minima
(d) no maxima or minima
Ans. (c)
Solution.
We have f(x) = 2x3 – 3x2 – 12x + 4
f ′(x) = 6x2 - 6x - 12
For local maxima and local minima f ′(x) = 0
∴ 6x2 - 6x - 12 = 0
⇒ x2 – x – 2 = 0 ⇒ x2 – 2x + x – 2 = 0
⇒ x(x – 2) + 1(x – 2) = 0 ⇒ (x + 1) (x - 2) = 0
⇒ x = -1, 2 are the points of local maxima and local minima
Now f ″(x) = 12x - 6
f ″(x)x = - 1 = 12(-1) - 6 = - 12 - 6 = - 18 < 0, maxima
f ″(x)x = 2 = 12(2) - 6 = 24 - 6 = 18 > 0 minima
So, the function is maximum at x = -1 and minimum at x = 2
Hence, the correct option is (c).
Q.55. The maximum value of sin x . cos x is
(a) 1/4
(b) 1/2
(c) √2
(d) 2√2
Ans. (b)
Solution.
We have f (x) = sin x cos x
⇒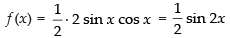
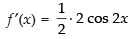
⇒ f ′(x) = cos 2x
Now for local maxima and local minima f ′(x) = 0
∴ cos 2x = 0
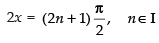
⇒
∴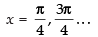
f ″(x) = - 2 sin 2x
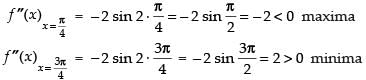
So f (x) is maximum at
∴ Maximum value of f(x) =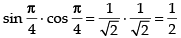
Hence, the correct option is (b).
Q.56. At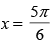 , f (x) = 2 sin3x + 3 cos3x is:
, f (x) = 2 sin3x + 3 cos3x is:
(a) maximum
(b) minimum
(c) zero
(d) neither maximum nor minimum
Ans. (a)
Solution.
We have f (x) = 2 sin 3x + 3 cos 3x
f ′(x) = 2 cos 3x × 3 - 3 sin 3x×3 = 6 cos 3x - 9 sin 3x
f ″(x) = - 6 sin 3x × 3 - 9 cos 3x × 3
= - 18 sin 3x - 27 cos 3x
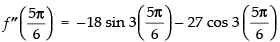

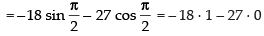
=– 18 < 0
maxima Maximum value of f(x) at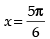
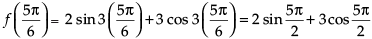
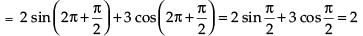
Hence, the correct option is (a).
Q.57. Maximum slope of the curve y = –x3 + 3x2 + 9x – 27 is:
(a) 0
(b) 12
(c) 16
(d) 32
Ans. (b)
Solution.
Given that y = – x3 + 3x2 + 9x – 27
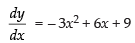
∴ Slope of the given curve,
m = – 3x2 + 6x + 9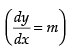
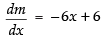
For local maxima and local minima,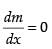
∴– 6x + 6 = 0 ⇒ x = 1
Now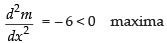
Maximum value of the slope at x = 1 is
mx = 1 = – 3(1)2 + 6(1) + 9 = – 3 + 6 + 9 = 12
Hence, the correct option is (b).
Q.58. f (x) = xx has a stationary point at
(a) x = e
(b)x = 1/e
(c) x = 1
(d) x =√e
Ans. (b)
Solution.
We have f (x) = xx
Taking log of both sides, we have
log f (x) = x log x
Differentiating both sides w.r.t. x, we get
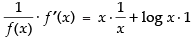
⇒ f ′(x) = f (x) [1 + log x] = xx [1 + log x]
To find stationary point, f ′(x) = 0
∴ xx[1 + log x] = 0
xx ≠ 0 ∴ 1 + log x = 0
⇒ log x = – 1 x = e–1 ⇒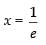
Hence, the correct option is (b).
Q.59. The maximum value of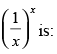
(a) e
(b) ee
(c) e1/e
(d)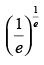
Ans. (c)
Solution.
Let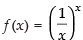
Taking log on both sides, we get
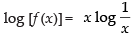
⇒ log [f (x)] = x log x-1 ⇒ log [f (x)] = - [x log x]
Differentiating both sides w.r.t. x, we get
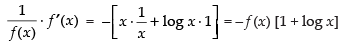
⇒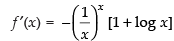
For local maxima and local minima f ′(x) = 0
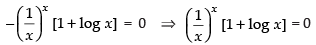
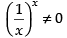
∴ 1 + log x = 0 ⇒ log x = – 1 ⇒ x = e–1
So,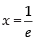 is the stationary point.
is the stationary point.
Now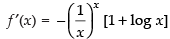
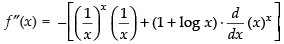
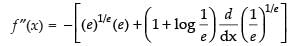
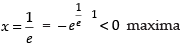
∴ Maximum value of the function at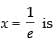
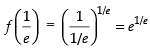
Hence, the correct option is (c).
Fill in the blanks
Q.60. The curves y = 4x2 + 2x – 8 and y = x3 – x + 13 touch each other at the point_____.
Ans.
We have
y = 4x2 + 2x – 8 ...(i)
and y = x3 – x + 13 ...(ii)
Differentiating eq. (i) w.r.t. x, we have
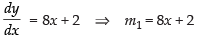
[m is the slope of curve (i)]
Differentiating eq. (ii) w.r.t. x, we get
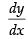 = 3x2 – 1 ⇒ m2 = 3x2 – 1
= 3x2 – 1 ⇒ m2 = 3x2 – 1
[m2 is the slope of curve (ii)]
If the two curves touch each other, then m1 = m2
∴ 8x + 2 = 3x2 – 1
⇒ 3x2 – 8x – 3 = 0 ⇒ 3x2 - 9x + x - 3 = 0
⇒ 3x(x - 3) + 1(x - 3) = 0 ⇒ (x - 3) (3x + 1) = 0
∴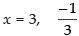
Putting x = 3 in eq. (i), we get
y = 4(3)2 + 2(3) – 8 = 36 + 6 – 8 = 34
So, the required point is (3, 34)
Now for x =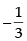
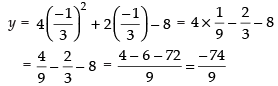
∴ Other required point is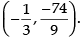
Hence, the required points are (3, 34) and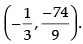
Q.61. The equation of normal to the curve y = tanx at (0, 0) is ________.
Ans.
We have y = tan x. So,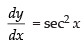
∴ Slope of the normal =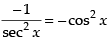
at the point (0, 0) the slope = – cos2 (0) = –1
So the equation of normal at (0, 0) is y – 0 = –1(x – 0)
⇒ y = – x ⇒ y + x =0
Hence, the required equation is y + x = 0.
Q.62. The values of a for which the function f (x) = sinx – ax + b increases on R are ______.
Ans.
We have f (x) = sin x – ax + b ⇒ f ′(x) = cos x - a
For increasing the function f ′(x) > 0
∴ cos x - a > 0
Since cos x ∈ [ - 1, 1]
∴ a < –1 ⇒ a ∈ ( - ∞, - 1)
Hence, the value of a is ( - ∞, - 1).
Q.63. The function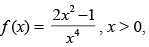 decreases in the interval _______.
decreases in the interval _______.
Ans.
We have f (x) =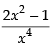
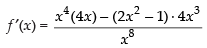
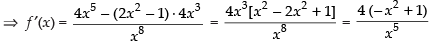
For decreasing the function f ′(x) < 0
∴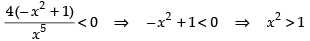
∴ x > ± 1 ⇒ x ∈ (1, ∞)
Hence, the required interval is (1, ∞).
Q.64. The least value of the function f (x) =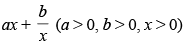
is ______.
Ans.
Here,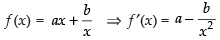
For maximum and minimum value f ′(x) = 0
∴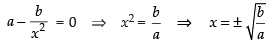
Now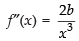
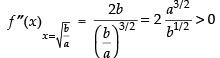 (∵ a, b > 0)
(∵ a, b > 0)
Hence,
minima So the least value of the function at x
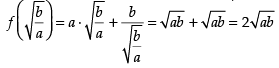
Hence, least value is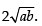
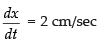
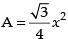
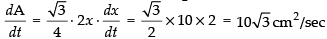

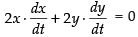
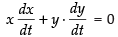
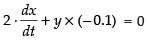 [∵ x = 2m]
[∵ x = 2m]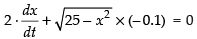
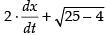 x (- 0.1) = 0
x (- 0.1) = 0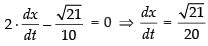
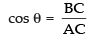 (θ is in radian)
(θ is in radian)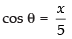
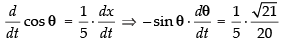
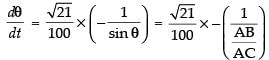
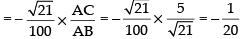 radian/sec
radian/sec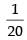 radian/sec
radian/sec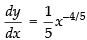
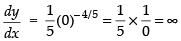
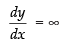
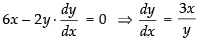
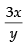 is the slope of the tangent
is the slope of the tangent

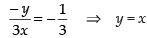
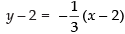
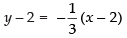
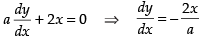
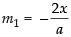
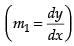
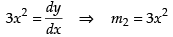
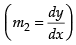
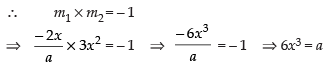
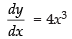

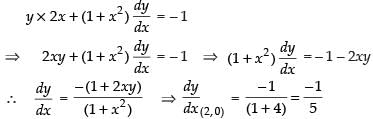
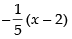
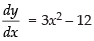

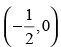
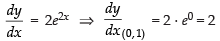
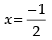
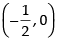

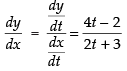
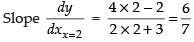
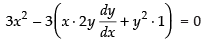
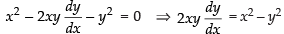
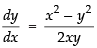
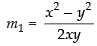

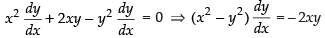
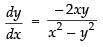
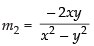
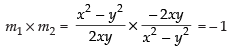
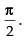
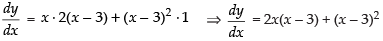
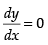
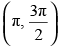
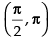
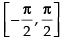
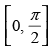
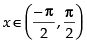
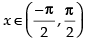 and f ′(x) < 0
and f ′(x) < 0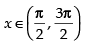

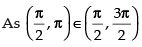
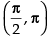
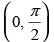
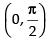
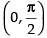
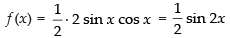
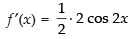
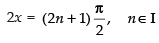

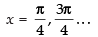
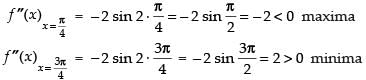

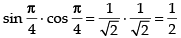
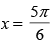 , f (x) = 2 sin3x + 3 cos3x is:
, f (x) = 2 sin3x + 3 cos3x is: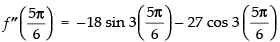

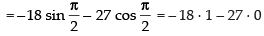
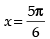
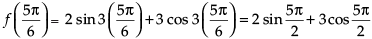
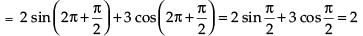
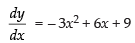
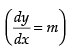
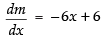
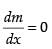
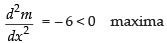
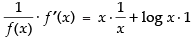
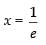
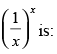
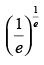
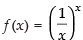
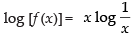
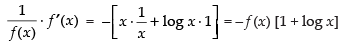
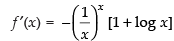
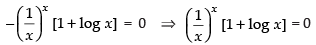
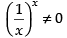
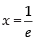 is the stationary point.
is the stationary point.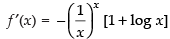
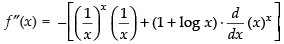
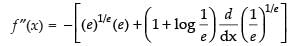
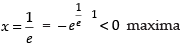
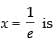
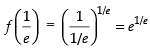
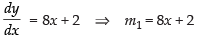
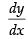 = 3x2 – 1 ⇒ m2 = 3x2 – 1
= 3x2 – 1 ⇒ m2 = 3x2 – 1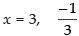
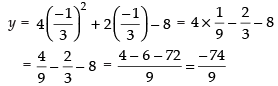
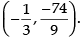
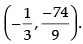
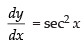
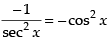
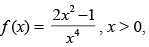 decreases in the interval _______.
decreases in the interval _______.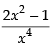
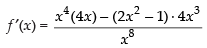
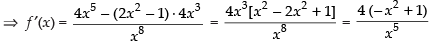
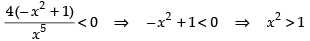
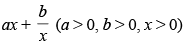
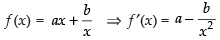
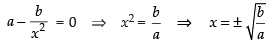
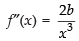
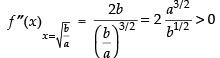 (∵ a, b > 0)
(∵ a, b > 0)