NCERT Exemplar: Application of Integrals | Mathematics (Maths) for JEE Main & Advanced PDF Download

Q.1. Find the area of the region bounded by the curves y² = 9x, y = 3x.
Ans.
We have, y² = 9x, y = 3x
Solving the two equations, we have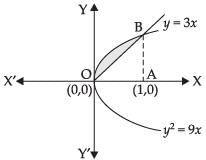

(3x)² = 9x
⇒ 9x² – 9x = 0 ⇒ 9x (x - 1) = 0
∴ x = 0, 1 Area of the shaded region
= ar (region OAB) – ar (DOAB)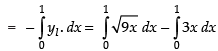


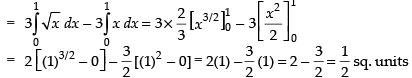
Hence, the required area =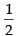sq. units.

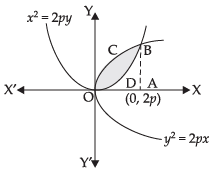
Q.2. Find the area of the region bounded by the parabola y² = 2px, and x² = 2py.
Ans.
We are given that: x² = 2py ...(i)
and y² = 2px ...(ii)
From eqn. (i) we get y =

Putting the value of y in eqn. (ii) we have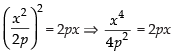

⇒ x⁴ = 8p³x ⇒ x⁴ – 8p³x = 0
⇒ x (x³ – 8p³) = 0 ∴ x = 0, 2p
Required area = Area of the region (OCBA – ODBA)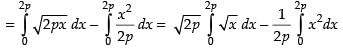



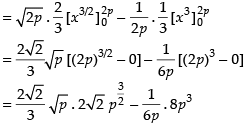
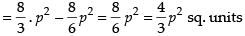
Hence, the required area =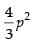sq. units.

Q.3. Find the area of the region bounded by the curve y = x³ and y = x + 6 and x = 0.
Ans.
We are given that: y = x³, y = x + 6 and x = 0
Solving y = x³ and y = x + 6, we get
x + 6 = x³
⇒ x³ – x – 6 = 0
⇒ x² (x – 2) + 2x (x – 2) + 3 (x – 2) = 0
⇒ (x – 2) (x² + 2x + 3) = 0
x² + 2x + 3 = 0 has no real roots. ∴ x = 2
∴ Required area of the shaded region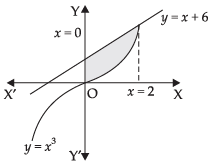


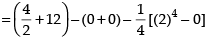
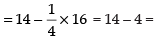10 sq. units.

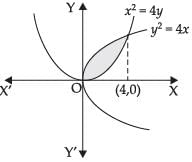
Q.4. Find the area of the region bounded by the curve y² = 4x, x² = 4y.
Ans.
We have y² = 4x and x² = 4y.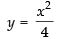

⇒

⇒
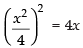
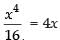
⇒ x⁴ = 64x ⇒ x⁴ – 64x = 0
⇒ x(x³ – 64) = 0
∴ x = 0, x = 4
Required area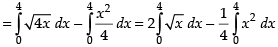


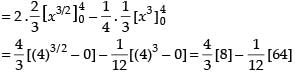
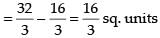
Hence, the required area =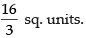

Q.5. Find the area of the region included between y² = 9x and y = x
Ans.
Given that: y² = 9x ...(i)
and y = x...(ii)
Solving eqns. (i) and (ii) we have
x² = 9x ⇒ x² – 9x = 0
x (x – 9) = 0 ∴ x = 0, 9
Required area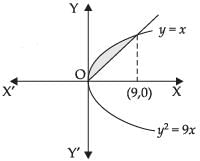





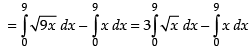
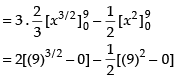
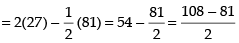
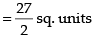
Hence, the required area =

Q.6. Find the area of the region enclosed by the parabola x² = y and the line y = x + 2
Ans.
Here, x² = y and y = x + 2
∴ x² = x + 2
⇒ x² – x – 2 = 0
⇒ x² – 2x + x – 2 = 0
⇒ x(x –2) + 1 (x – 2) = 0
⇒ (x – 2) (x + 1) = 0
∴ x = –1, 2
Graph of y = x + 2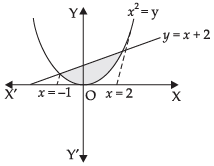


Area of the required region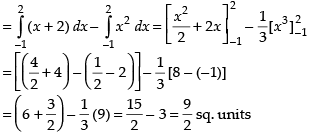

Hence, the required area =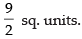

Q.7. Find the area of region bounded by the line x = 2 and the parabola y² = 8x
Ans.
Here, y² = 8x and x = 2
y² = 8(2) = 16
∴ y = ±4
Required area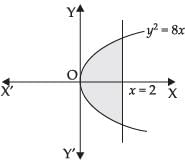



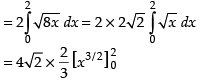
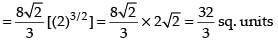
Hence, the area of the region =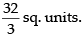

Q.8. Sketch the region {(x, 0) : y =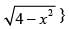and x-axis. Find the area of the region using integration.
Ans.
Given that {(x, 0) : y =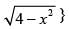 
⇒ y² = 4 – x²
⇒ x² + y² = 4 which is a circle.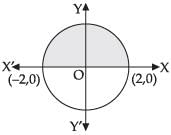

Required area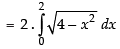

[Since circle is symmetrical about y-axis]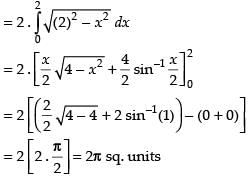

Hence, the required area = 2π sq. units.

Q.9. Calculate the area under the curve y = 2 √x included between the lines x = 0 and x = 1.
Ans.
Given the curves y = 2√x , x = 0 and x = 1.
y = 2√x ⇒ y² = 4x (Parabola)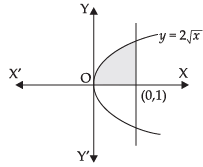

Required area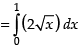

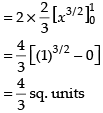
Hence, required area =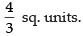

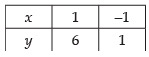
Q.10. Using integration, find the area of the region bounded by the line 2y = 5x + 7, x-axis and the lines x = 2 and x = 8.
Ans.
Given that: 2y = 5x + 7, x-axis, x = 2 and x = 8.
Let us draw the graph of 2y = 5x + 7 ⇒ y =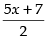


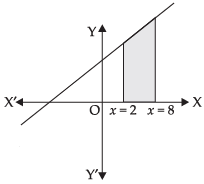
Area of the required shaded region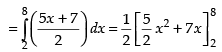

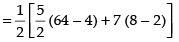
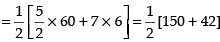
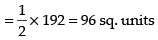
Hence, the required area = 96 sq. units.

Q.11. Draw a rough sketch of the curve y =in the interval [1, 5]. Find the area under the curve and between the lines x = 1 and x = 5.
Ans.
Here, we have y =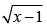 

⇒ y² = x – 1 (Parabola)
Area of the required region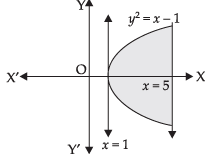



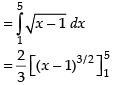
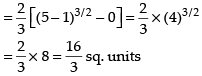
Hence, the required area =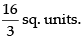

Q.12. Determine the area under the curve y =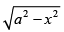 included between the lines x = 0 and x = a.
Ans.
Here, we are given y =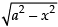

⇒ y² = a² – x²

⇒ x² + y² = a² 
Area of the shaded region



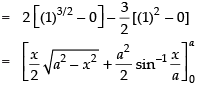
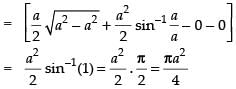
Hence, the required area =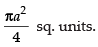

Q.13. Find the area of the region bounded by y = √x and y = x.
Ans.
We are given the equations of curve y = √x and line y = x.
Solving y = √x ⇒ y² = x and y = x, we get
x² = x ⇒ x² – x = 0
⇒ x (x – 1) = 0 ∴ x = 0, 1
Required area of the shaded region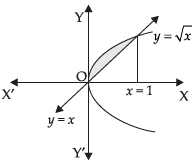



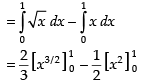
Hence, the required area =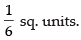

Q.14. Find the area enclosed by the curve y = –x² and the straight lilne x + y + 2 = 0.
Ans.
We are given that y = –x² or x² = –y
and the line x + y + 2 = 0
Solving the two equations, we get
x  – x² + 2 = 0
⇒ x²  – x – 2 = 0
⇒ x² – 2x + x – 2 = 0
⇒ x (x – 2) + 1 (x – 2) = 0
⇒ (x – 2) (x + 1) = 0
∴ x = –1, 2
Area of the required shaded region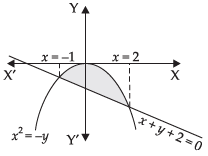


⇒
⇒
⇒
⇒

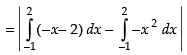
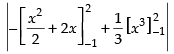
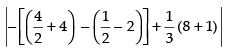
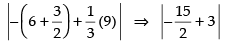
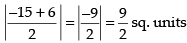
Q.15. Find the area bounded by the curve y = √x , x = 2y + 3 in the first quadrant and x-axis.
Ans.
Given that: y = √x , x = 2y + 3, first quadrant and x-axis.
Solving y = √x and x = 2y + 3, we get
y = 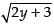 ⇒ y² = 2y + 3

⇒ y² – 2y – 3 = 0 ⇒ y² – 3y + y – 3 = 0
⇒ y(y – 3) + 1 (y – 3) = 0
⇒(y + 1) (y – 3) = 0
∴ y = –1, 3
Area of shaded region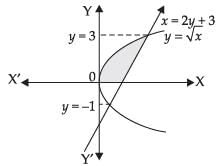



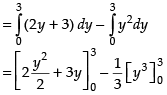
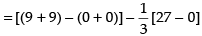
= 18 - 9 = 9 sq. units
Hence, the required area = 9 sq. units.

Long Answer (L.A.)
Q.16. Find the area of the region bounded by the curve y² = 2x and x² + y² = 4x.
Ans.
Equations of the curves are given by
x² + y² = 4x ...(i)
and y² = 2x ...(ii)
⇒ x² – 4x + y² = 0
⇒ x² – 4x + 4 – 4 + y² = 0
⇒  (x – 2)² + y² = 4
Clearly it is the equation of a circle having its centre (2, 0) and radius 2.
Solving x² + y² = 4x and y² = 2x
x² + 2x = 4x
⇒ x² + 2x – 4x = 0
⇒  x² – 2x = 0
⇒ x (x – 2) = 0
∴ x = 0, 2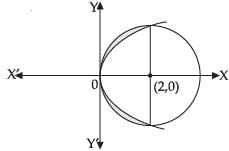

Area of the required region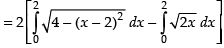

[∴ Parabola and circle both are symmetrical about x-axis.]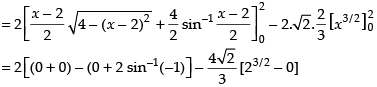


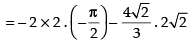
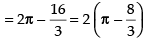sq. units
Hence, the required area =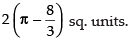

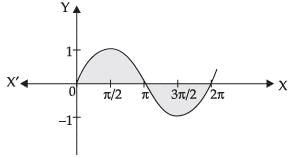
Q.17. Find the area bounded by the curve y = sinx between x = 0 and x = 2π.
Ans.
Required area =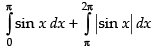




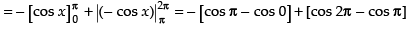
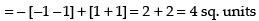
Q.18. Find the area of region bounded by the triangle whose vertices are (–1, 1), (0, 5) and (3, 2), using integration.
Ans.
The coordinates of the vertices of ΔABC are given by A(–1, 1), B (0, 5) and C (3, 2).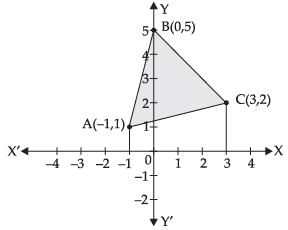

Equation of AB is y – 1 =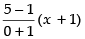
⇒ y – 1 = 4x + 4
∴ y = 4x + 4 + 1 ⇒ y = 4x + 5 ...(i)
Equation of BC is y – 5 =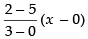
⇒ y – 5 = –x
∴ y = 5 – x ...(ii)
Equation of CA is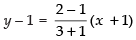

⇒
∴
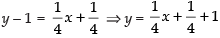
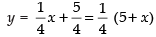
Area of ΔABC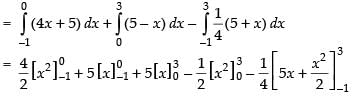






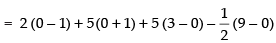
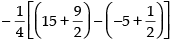
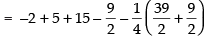
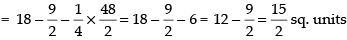
Q.19. Draw a rough sketch of the region {(x, y) : y² ≤ 6ax and x² + y² ≤ 16a²}. Also find the area of the region sketched using method of integration.
Ans.
Given that:
{(x, y) : y² ≤ 6ax and x² + y² ≤ 16a²}
Equation of Parabola is
y² = 6ax ...(i)
and equation of circle is
x² + y² ≤ 16a² ...(ii)
Solving eqns. (i) and (ii) we get
x² + 6ax = 16a²
⇒ x² + 6ax – 16a² = 0
⇒ x² + 8ax – 2ax – 16a² = 0
⇒ x(x + 8a) – 2a (x + 8a) = 0
⇒(x + 8a) (x – 2a) = 0
∴ x = 2a and x = – 8a. (Rejected as it is out of region)

Area of the required shaded region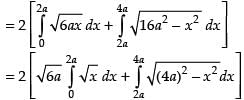






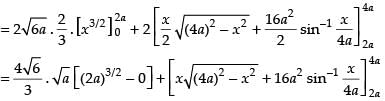
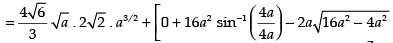
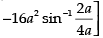
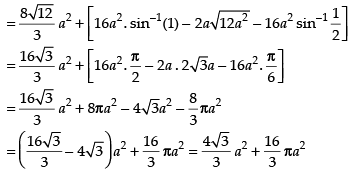
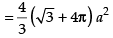
Hence, required area =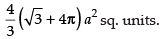

Q.20. Compute the area bounded by the lines x + 2y = 2, y – x = 1 and 2x + y = 7.
Ans.
Given that: x + 2y = 2 ...(i)
y – x = 1 ...(ii)
and 2x + y = 7 ...(iii)

Solving eqns. (ii) and (iii) we get
y = 1 + x
∴ 2x + 1 + x = 7
3x = 6
⇒ x = 2
∴ y = 1 + 2  = 3
Coordinates of B = (2, 3)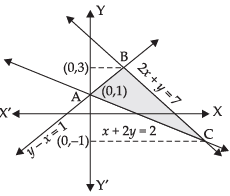

Solving eqns. (i) and (iii)
we get
x + 2y = 2
∴ x = 2 – 2y
2x + y = 7
2(2 – 2y) + y = 7
⇒ 4 – 4y + y = 7 ⇒ - 3y = 3
∴ y = –1 and x = 4
∴ Coordinates of C = (4, – 1) and coordinates of A = (0, 1).
Taking the limits on y-axis, we get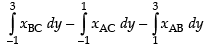




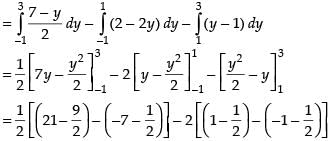
Hence, the required area = 6 sq. units.

Q.21. Find the area bounded by the lines y = 4x + 5, y = 5 – x and 4y = x + 5.
Ans.
Given that y = 4x + 5 ...(i)
y = 5 – x ...(ii)
and 4y = x + 5 ...(iii)


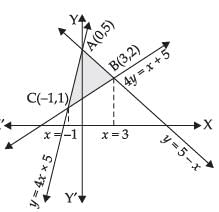
Solving eq. (i) and (ii) we get
4x + 5 = 5 – x
⇒ x = 0 and y = 5
∴ Coordinates of A = (0, 5)
Solving eq. (ii) and (iii)
y = 5 – x
4y = x + 5
5y = 10
∴ y = 2 and x = 3
∴ Coordinates of B = (3, 2)
Solving eq. (i) and (iii)
y = 4x + 5
4y = x + 5
⇒ 4 (4x + 5) = x + 5
⇒ 16x + 20 = x + 5 ⇒ 15x = - 15
∴ x = –1 and y = 1
∴ Coordinates of C = (–1, 1).
∴ Area of required regions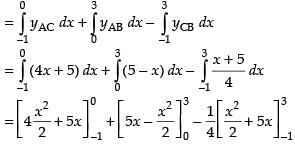



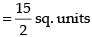
Hence, the required area =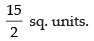

Q.22. Find the area bounded by the curve y = 2cosx and the x-axis from x = 0 to x = 2π.
Ans.
Given equation of the curve is y = 2 cos x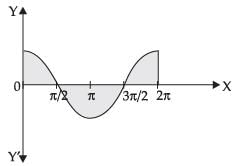

∴ Area of the shaded region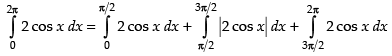





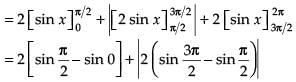
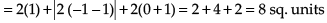
Q.23. Draw a rough sketch of the given curve y = 1 + |x +1|, x = –3, x = 3, y = 0 and find the area of the region bounded by them, using integration.
Ans.
Given equations are y = 1 + |x + 1|, x = –3
and x  = 3, y = 0
Taking y = 1 + |x + 1|
⇒ y = 1 + x + 1
⇒ y = x + 2 and y = 1 – x – 1 
⇒ y = –x
On solving we get x = –1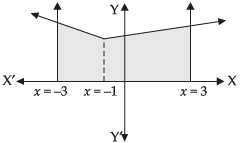

Area of the required regions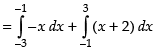


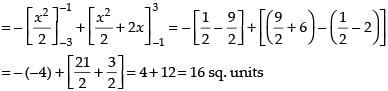
Hence, the required area = 16 sq. units.

Objective Type Questions
Q.24. The area of the region bounded by the y-axis, y = cosx and y = sinx, 0 ≤ x ≤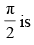
(a) √2 sq. units 
(b) ( √2 + 1) sq. units 
(c) ( √2 - 1) sq. units 
(d) (2√2 - 1) sq. units
Ans. (c)
Solution .
Given that y-axis, y = cos x, y = sin x,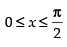 

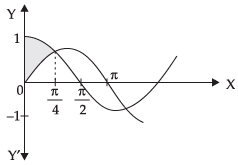
Required area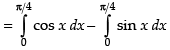

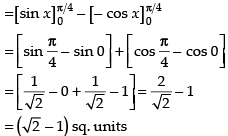
Hence, the correct option is (c).

Q.25. The area of the region bounded by the curve x² = 4y and the straight line x = 4y – 2 is
(a) 3/8 sq. units 
(b) 5/8 sq. units
(c) 7/8 sq. units
(d) 9/8 sq. units
Ans. (d)
Solution .
Given that: The equation of parabola is x² = 4y ...(i)
and equation of straight line is x = 4y – 2 ...(ii)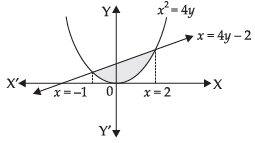

Solving eqn. (i) and (ii) we get


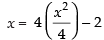
⇒ x = x² – 2
⇒ x² – x – 2 = 0 ⇒ x² – 2x + x – 2 = 0
⇒ x (x – 2) + 1 (x – 2) = 0 ⇒ (x – 2) (x + 1) = 0 ∴ x = –1, x = 2
Required area =

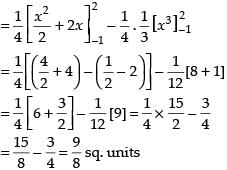
Hence, the correct option is (d).

Q.26. The area of the region bounded by the curve y =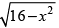and x-axis is 
(a) 8 sq units 
(b) 20π sq units  
(c) 16π sq units 
(d) 256π sq units
Ans. (a)
Solution .
Here, equation of curve is y =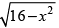 
Required area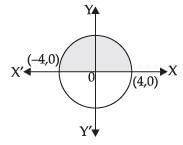


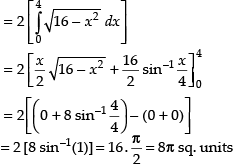
Hence, the correct option is (a).

Q.27. Area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x² + y² = 32 is 
(a) 16π sq units 
(b) 4π sq units 
(c) 32π sq units    
(d) 24 sq units
Ans. (b)
Solution .
Given equation of circle is  x² + y² = 32 ⇒ x² + y² = (4√2 )²
and the line is y = x and the x-axis.
Solving the two equations we have

x² + x² = 32
⇒ 2x² = 32
⇒ x² = 16
∴ x = ± 4
Required area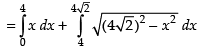



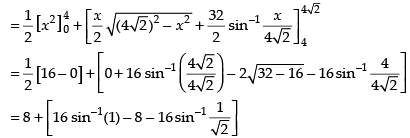
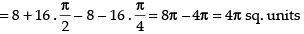
Hence, the correct option is (b).

Q.28. Area of the region bounded by the curve y = cosx between x = 0 and x = π is
(a) 2 sq. units 
(b) 4 sq. units 
(c) 3 sq. units 
(d) 1 sq. units
Ans. (a)
Solution .
Given that: y = cos x, x = 0, x = π
Required area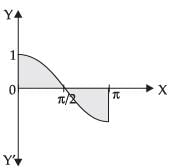



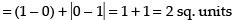
Hence, the correct option is (a).

Q.29. The area of the region bounded by parabola y² = x and the straight line 2y = x is
(a) 4/3 sq. units 
(b) 1 sq. unit
(c) 2/3 sq. units 
(d) 1/3 sq. units
Ans. (a)
Solution .
Given equation of parabola is y² = x ...(i)
and equation of straight line is 2y = x ...(ii)
Solving eqns. (i) and (ii) we get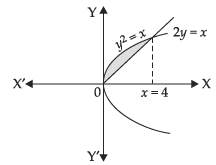


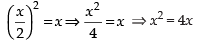
⇒ x(x – 4) = 0 ∴ x = 0, 4
Required area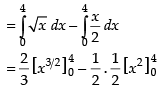



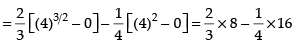
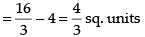
Hence, the correct answer is (a).

Q.30. The area of the region bounded by the curve y = sinx between the ordinates x = 0,and the x-axis is
(a) 2 sq. units 
(b) 4 sq. units 
(c) 3 sq. units 
(d) 1 sq. units
Ans. (d)
Solution .
Given equation of curve is y = sin x between x = 0 and x =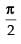

Area of required region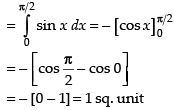

Hence, the correct answer is (d).

Q.31. The area of the region bounded by the ellipse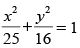 is
(a) 20π sq units 
(b) 20π² sq units 
(c) 16π² sq units 
(d) 25 π sq units
Ans. (a)
Solution .
Given equation of ellipse is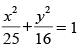 



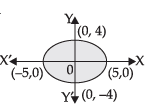
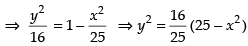
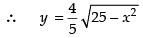
∴ Since the ellipse is symmetrical about the axes.
∴ Required area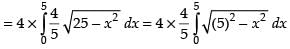

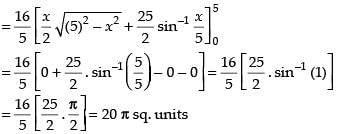
Hence, the correct answer is (a).

Q.32. The area of the region bounded by the circle x² + y² = 1 is 
(a) 2π sq units 
(b) π sq units 
(c) 3π sq units 
(d) 4π sq units
Ans. (b)
Solution .
Given equation of circle is
x² + y² = 1  y =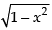

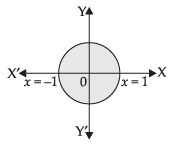
Since the circle is symmetrical about the axes.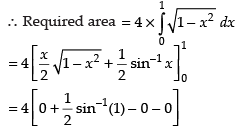


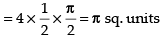
Hence, the correct answer is (b).

Q.33. The area of the region bounded by the curve y = x + 1 and the lines x = 2 and x = 3 is
(a) 7/2 sq. units 
(b) 9/2 sq. units 
(c) 11/2 sq. units
(d) 13/2 sq. units
Ans. (a)
Solution .
Given equation of lines are
y = x + 1, x = 2 and x = 3
Required area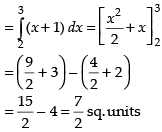


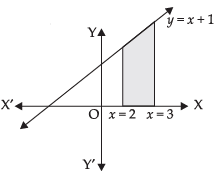
Hence, the correct option is (a).

Q.34. The area of the region bounded by the curve x = 2y + 3 and the y lines. y = 1 and y = –1 is

(a) 4 sq. units
(b) 3/2 sq. units 

(c) 6 sq. units
(d) 8 sq. units
Ans. (c)
Solution .
Given equations of lines are x = 2y + 3,  y = 1 and y = –1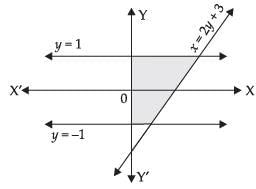

Required area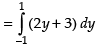

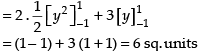
Hence, the correct answer is (c).