NCERT Exemplar: Continuity and Differentiability- 1 | Mathematics (Maths) for JEE Main & Advanced PDF Download
Q.1. Examine the continuity of the function
f(x) = x3 + 2x2 – 1 at x = 1
Ans.
We know that y = f(x) will be continuous at x = a if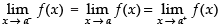
Given: f(x) = x3 + 2x2 – 1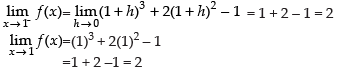
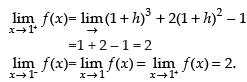
Hence, f(x) is continuous at x = 1.
Find which of the functions in Exercises 2 to 10 is continuous or discontinuous at the indicated points:
Q.2. 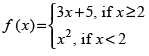 at x = 2
at x = 2
Ans.
Since
Hence f (x) is discontinuous at x = 2.
Q.3. 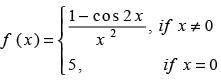 at x = 0
at x = 0
Ans.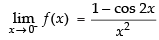
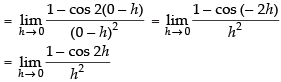
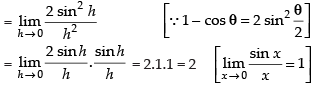
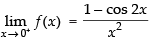
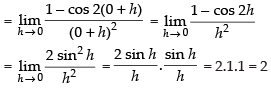
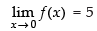
As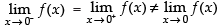
∴ f(x) is discontinuous at x = 0.
Q.4. 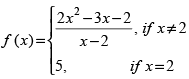 at x = 2
at x = 2
Ans.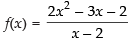
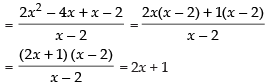
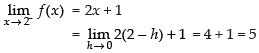
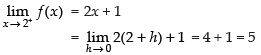
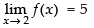
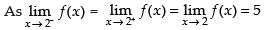
Hence, f(x) is continuous at x = 2.
Q.5. 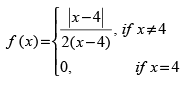 at x = 4
at x = 4
Ans.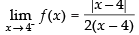
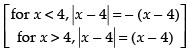
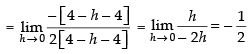
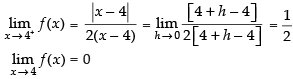
∴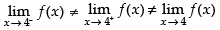
Hence, f(x) is discontinuous at x = 4.
Q.6. 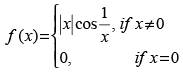 at x = 0
at x = 0
Ans.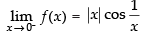
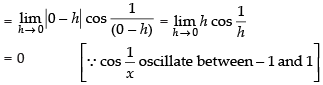
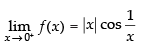
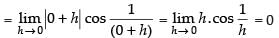
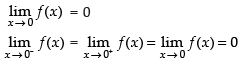
Hence, f(x) is continuous at x = 0.
Q.7. 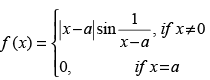 at x = a
at x = a
Ans.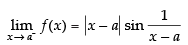
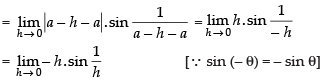
= 0 × [a number oscillating between – 1 and 1]
= 0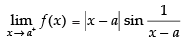
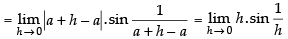
= 0 × [a number oscillating between – 1 and 1]
As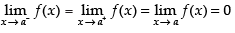
Hence, f(x) is continuous at x = a.
Q.8. 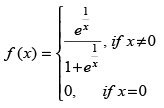 at x = 0
at x = 0
Ans.
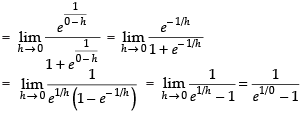
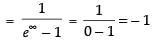 [∵ e∞ = 0]
[∵ e∞ = 0]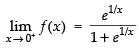
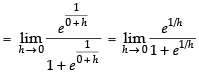
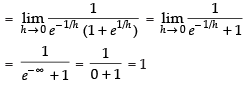 [e– ∞= 0]
[e– ∞= 0]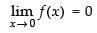
As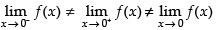
Hence, f(x) is discontinuous at x = 0.
Q.9. 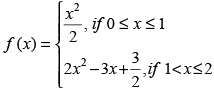 at x = 1
at x = 1
Ans.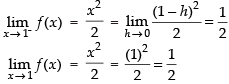
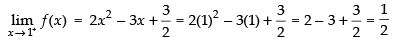
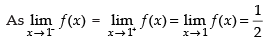
Hence, f(x) is continuous at x = 1.
Q.10. 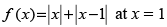
Ans.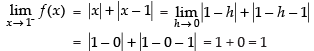
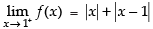
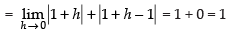
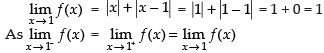
Hence, f(x) is continuous at x = 1.
Find the value of k in each of the Exercises 11 to 14 so that the function f is continuous at the indicated point:
Q.11.  at x = 5
at x = 5
Ans.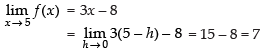
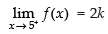
As the function is continuous at x = 5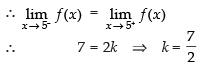
Hence, the value of k is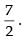
Q.12. 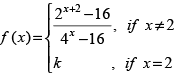 at x = 2
at x = 2
Ans.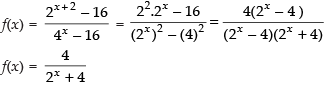
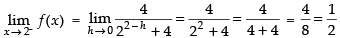
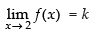
As the function is continuous at x = 2.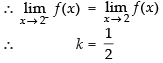
Hence, value of k is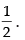
Q.13. 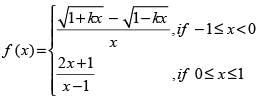 at x = 0
at x = 0
Ans.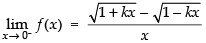
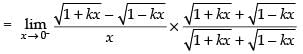
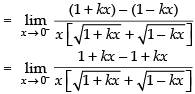
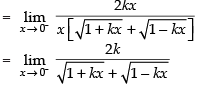
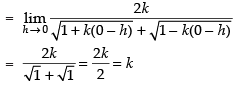
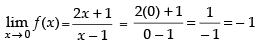
As the function is continuous at x = 0.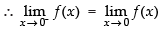
k = – 1
Hence, the value of k is – 1.
Q.14. 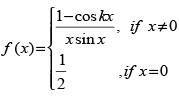 at x = 0
at x = 0
Ans.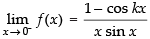
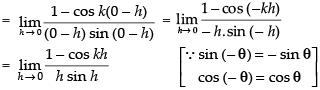
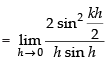
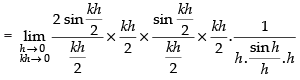


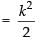

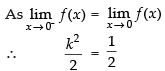
⇒ k2 = 1 ⇒ k = ± 1
Hence, the value of k is ± 1.
Q.15. Prove that the function f defined by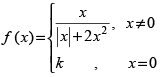
remains discontinuous at x = 0, regardless the choice of k.
Ans.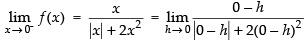
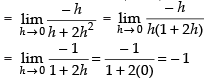
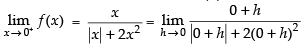
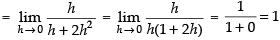
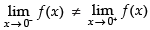
Hence, f(x) is discontinuous at x = 0 regardless the choice of k.
Q.16. Find the values of a and b such that the function f defined by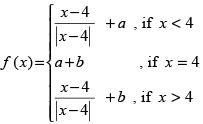
is a continuous function at x = 4.
Ans.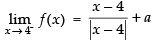
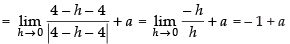
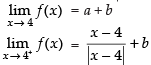
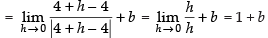
As the function is continuous at x = 4.
∴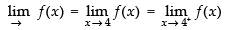
– 1 + a = a + b = 1 + b
∴ – 1 + a=a + b ⇒ b = – 1
1 + b =a + b ⇒ a = 1
Hence, the value of a = 1 and b = – 1.
Q.17. Given the function f (x) =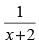 Find the points of discontinuity of the composite function y = f (f (x)).
Find the points of discontinuity of the composite function y = f (f (x)).
Ans.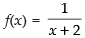
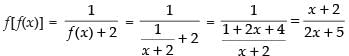
∴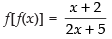
This function will not be defined and continuous where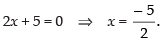
Hence,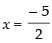 is the point of discontinuity.
is the point of discontinuity.
Q.18 Find all points of discontinuity of the function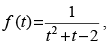
where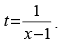
Ans.
We have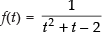
⇒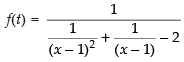
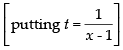
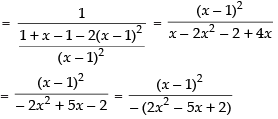
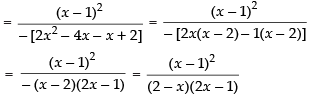
So, if f(t) is discontinuous, then 2 – x = 0
∴ x = 2 and 2x – 1 = 0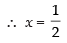
Hence, the required points of discontinuity are 2 and 1/2.
Q.19. Show that the function f(x) = sin x + cos x is continuous at x = π.
Ans.
Given that f(x) =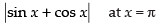
Put g(x) = sin x + cos x and h(x) =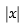
∴ h[g(x)] = h(sin x + cos x) =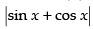
Now, g(x) = sin x + cos x is a continuous function since sin x and cos x are two continuous functions at x = π.
We know that every modulus function is a continuous function everywhere.
Hence, f(x) =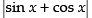 is continuous function at x = π.
is continuous function at x = π.
Examine the differentiability of f, where f is defined by
Q.20.  at x = 2.
at x = 2.
Ans.
We know that a function f is differentiable at a point ‘a’ in its domain if
Lf ′(c) = Rf ′(c)
where Lf ′(c) =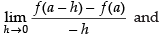
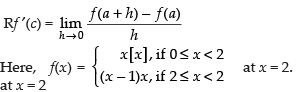
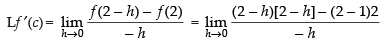
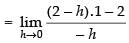
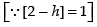
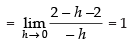
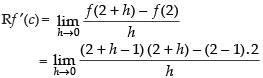
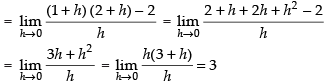
Lf ′(2) ≠ Rf ′(2)
Hence, f(x) is not differentiable at x = 2.
Q.21. Examine the differentiability of f, where f is defined by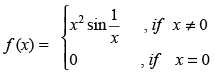 at x = 0.
at x = 0.
Ans.
Given that: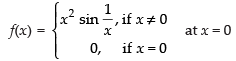
For differentiability we know that:′
Lf ′(c) = Rf ′(c)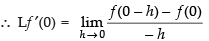


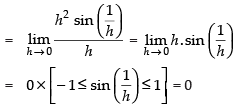
So, Lf ′(0) = Rf ′(0) = 0
Hence, f(x) is differentiable at x = 0.
Q.22. 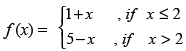 at x = 2.
at x = 2.
Ans.
f(x) is differentiable at x = 2 if
Lf ′(2) = Rf ′(2)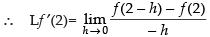
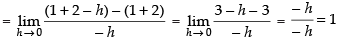
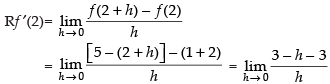
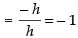
So, Lf ′(2) ≠ Rf ′(2)
Hence, f(x) is not differentiable at x = 2.
Q.23. Show that f(x) = 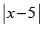 is continuous but not differentiable at x = 5.
is continuous but not differentiable at x = 5.
Ans.
We have f(x) =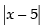
⇒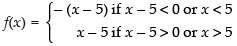
For continuity at x = 5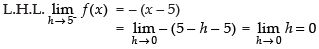
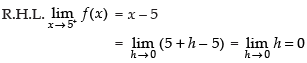
L.H.L. = R.H.L.
So, f(x) is continuous at x = 5.
Now, for differentiability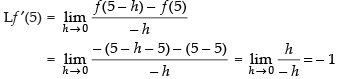
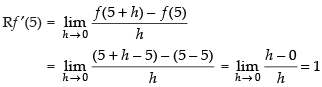
∵ Lf ′(5) ≠ Rf ′(5)
Hence, f(x) is not differentiable at x = 5.
Q.24. A function f : R → R satisfies the equation f( x + y) = f(x) f(y) for all x, y ∈ R, f(x) ≠ 0. Suppose that the function is differentiable at x = 0 and f ′ (0) = 2. Prove that f ′(x) = 2 f (x).
Ans.
Given that: f : R → R satisfies the equation f(x + y) = f(x).f(y) ∀ x, y ∈ R, f(x) ≠ 0.
Let us take any point x = 0 at which the function f(x) is differentiable.
∴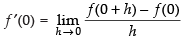
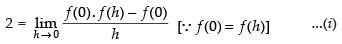
⇒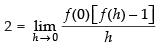
Now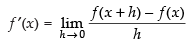
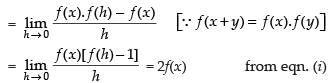
Hence, f′(x) = 2f(x).
Differentiate each of the following w.r.t. x (Exercises 25 to 43) :
Q.25.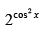
Ans.
Let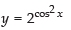
Taking log on both sides, we get
Differentiating both sides w.r.t. x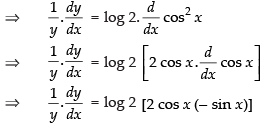
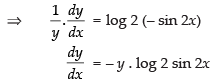
Hence,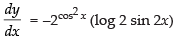
Q.26.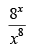
Ans.
Let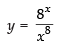
Taking log on both sides, we get, log y =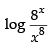
⇒ log y = log 8x – log x8 ⇒ log y = x log 8 – 8 log x
Differentiating both sides w.r.t. x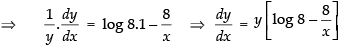
Hence,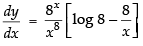
Q.27.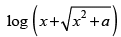
Ans.
Let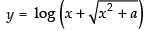
Differentiating both sides w.r.t. x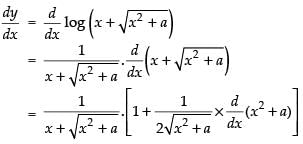
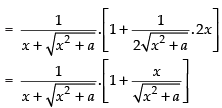
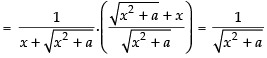
Hence,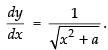
Q.28. log [log (log x5 )]
Ans.
Let y = log [log (log x5 )]
Differentiating both sides w.r.t. x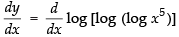
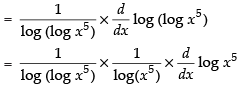

Hence,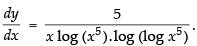
Q.29. sin √x + cos2 √x
Ans.
Let y = sin √x + cos2 √x
Differentiating both sides w.r.t. x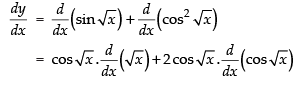
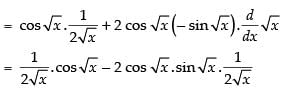
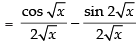
Hence,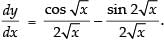
Q.30. sinn (ax2 + bx + c)
Ans.
Let y = sinn (ax2 + bx + c)
Differentiating both sides w.r.t. x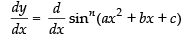
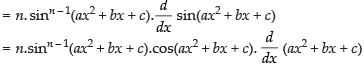
= n.sinn – 1(ax2 + bx + c).cos(ax2 + bx + c).(2ax + b)
Hence,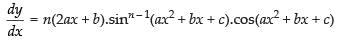
Q.31. 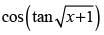
Ans.
Let y =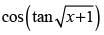
Differentiating both sides w.r.t. x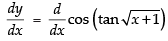

Hence,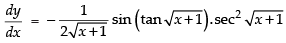
Q.32. sinx2 + sin2x + sin2(x2)
Ans.
Let y = sinx2 + sin2x + sin2(x2)
Differentiating both sides w.r.t. x,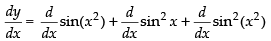
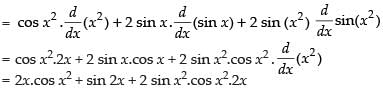
Hence,
Q.33.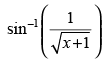
Ans.
Let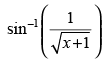
Differentiating both sides w.r.t. x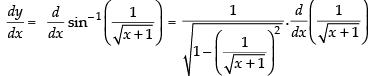
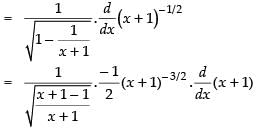
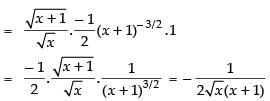
Hence,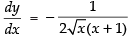
Q.34. ( sin x )cos x
Ans.
Let y = (sin x)cos x
Taking log on both sides,
log y = log (sin x)cos x
⇒ log y = cos x.log (sin x) [∵ log xy = y log x]
Differentiating both sides w.r.t. x,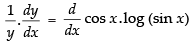

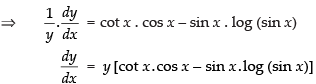
Hence,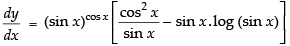
Q.35. sinmx . cosnx
Ans.
Let y = sinm x . cosn x
Differentiating both sides w.r.t. x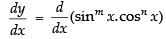
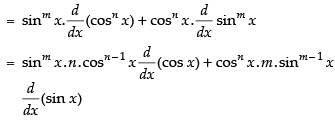
= n.sinm x.cosn – 1 x.(– sin x) + m.cosn x.sinm –1 x.cos x
= – n.sinm + 1 x.cosn – 1 x + m cosn + 1 x. sinm – 1x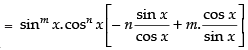
Hence,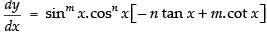
Q.36. (x + 1)2 (x + 2)3 (x + 3)4
Ans.
Let y = (x + 1)2(x + 2)3(x + 3)4
Taking log on both sides,
log y = log [( x + 1)2 .(x+ 2)3 .( x + 3)4 ]
⇒ log y = log (x + 1)2 + log (x + 2)3 + log (x + 3)4
[∵ log xy = log x + log y]
⇒ log y = 2 log (x + 1) + 3 log (x + 2) + 4 log (x + 3)
[∵ log xy = y log x]
Differentiating both sides w.r.t. x,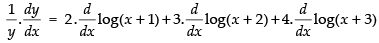
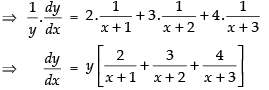
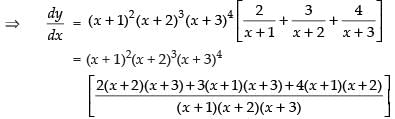
= (x + 1)(x + 2)2(x + 3)3(2x2 + 10x + 12 + 3x2 + 12x + 9 + 4 x2 + 12x + 8)
= (x + 1)(x + 2)2(x + 3)3(9x2 + 34x + 29)
Hence,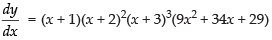
Q.37.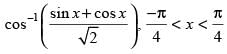
Ans.
Let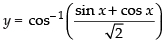
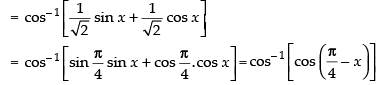
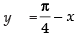
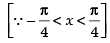
Differentiating both sides w.r.t. x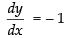
Q.38.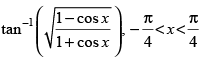
Ans.
Let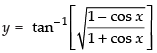
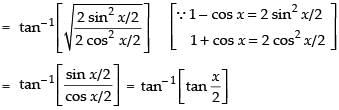
∵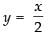
Differentiating both sides w.r.t. x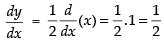
Hence,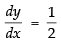
Q.39. 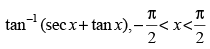
Ans.
Let y = tan– 1(sec x + tan x)
Differentiating both sides w.r.t. x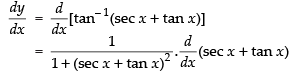
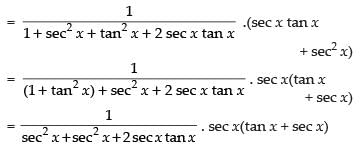
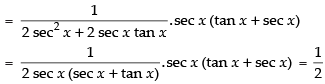
Hence,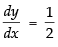
Alternate solution
Let y =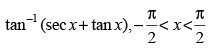
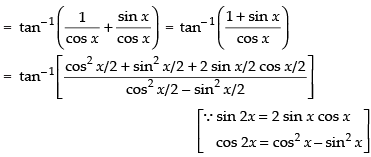
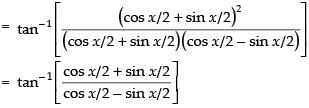
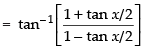 [Dividing the Nr. and Den. by cos x/2]⇒
[Dividing the Nr. and Den. by cos x/2]⇒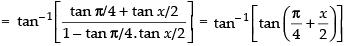
∴
Differentiating both sides w.r.t. x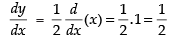
Hence,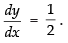
Q.40.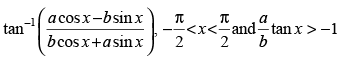
Ans.
Let
⇒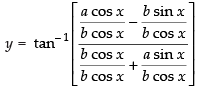
⇒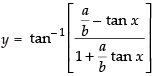
⇒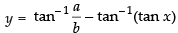
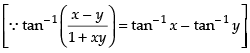
⇒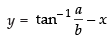
Differentiating both sides with respect to x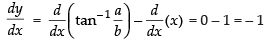
Hence,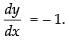
Q.41. 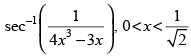
Ans.
Let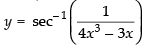
Put x = cos θ ∴ θ = cos– 1 x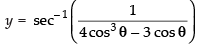
⇒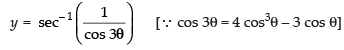
⇒ y = sec– 1 (sec 3θ) ⇒ y = 3θ
y = 3 cos– 1 x
Differentiating both sides w.r.t. x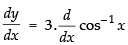
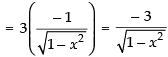
Hence,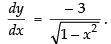
Q.42.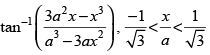
Ans.
Let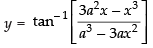
Put x = a tan θ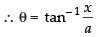
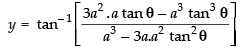
⇒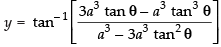
⇒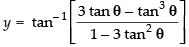
⇒ y = tan - 1[tan 3θ]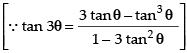
⇒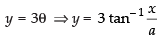
Differentiating both sides w.r.t. x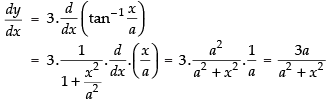
Hence,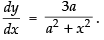
Q.43.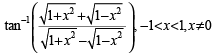
Ans.
Let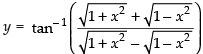
Putting x2 = cos 2θ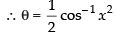
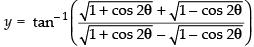
⇒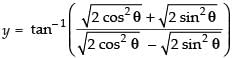
⇒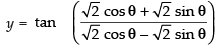
⇒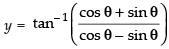
⇒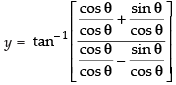
⇒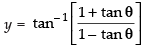
⇒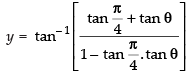
⇒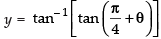
⇒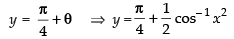
Differentiating both sides w.r.t. x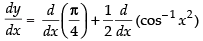
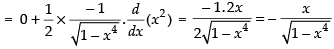
Hence,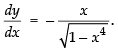
Find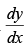 of each of the functions expressed in parametric form in Exercises from 44 to 48.
of each of the functions expressed in parametric form in Exercises from 44 to 48.
Q.44.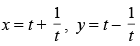
Ans.
Given that: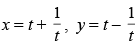
Differentiating both the given parametric functions w.r.t. t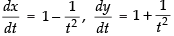
∴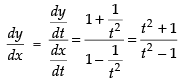
Hence,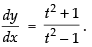
Q.45.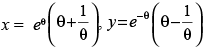
Ans.
Given that: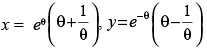
Differentiating both the parametric functions w.r.t. θ.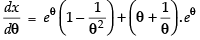
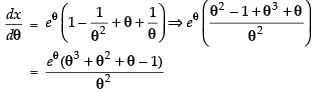
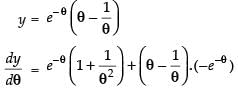
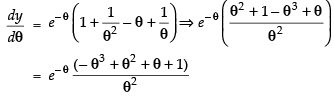
∴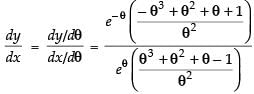
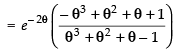
Hence,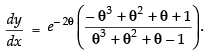
Q.46. x = 3cosθ – 2cos3θ, y = 3sinθ – 2sin3θ.
Ans.
Given that: x = 3cosθ – 2cos3θ, y = 3sinθ – 2sin3θ.
Differentiating both the parametric functions w.r.t. θ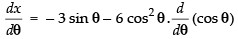
= – 3 sin θ – 6 cos2 θ . (– sin θ)
= – 3 sin θ + 6 cos2 θ . sin θ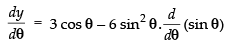
= 3 cos θ – 6 sin2 θ . cos θ
∴
⇒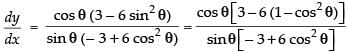
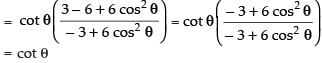
Hence,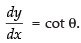
Q.47. 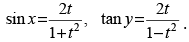
Ans.
Given that sin x =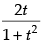
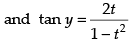
∴ Taking sin x =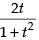
Differentiating both sides w.r.t t, we get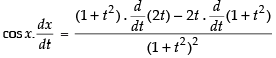
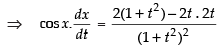
⇒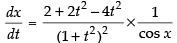
⇒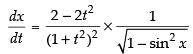
⇒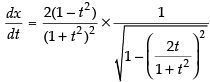
⇒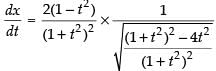
⇒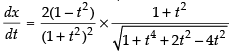
⇒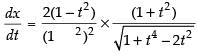
⇒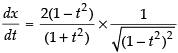
⇒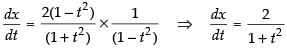
Now taking, tan y =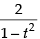
Differentiating both sides w.r.t, t, we get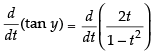

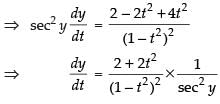
⇒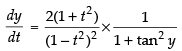
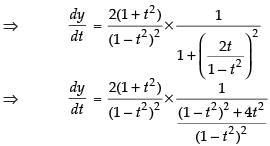
⇒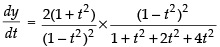
⇒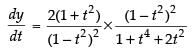
⇒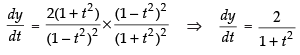
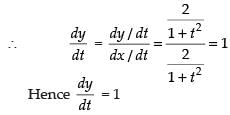
Q.48. 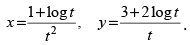
Ans.
Given that: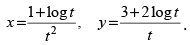
Differentiating both the parametric functions w.r.t. t
Q.49. If x = ecos2t and y = esin2t, prove that
Ans.
Given that: x = ecos2t and y = esin2t
⇒ cos 2t = log x and sin 2t = log y.
Differentiating both the parametric functions w.r.t. t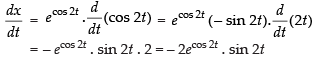
Now y = esin2t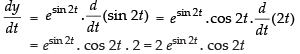
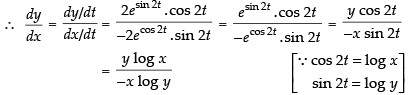
Hence,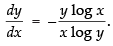
Q.50. If x = a sin2t (1 + cos2t) and y = b cos2t (1–cos2t), show that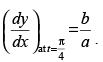
Ans.
Given that: x = a sin 2t (1 + cos 2t) and y = b cos 2t (1 – cos 2t).
Differentiating both the parametric functions w.r.t. t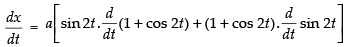
= a [sin 2t . ( - sin 2t).2 + (1+ cos 2t) (cos 2t).2]
= a[- 2 sin 2 2t + 2 cos 2t+ 2 cos2 2t]
= a[2(cos2 2t - sin2 2t)+ 2 cos 2t]
= a [2 cos 4t + 2 cos 2t] [∵ cos 2x = cos2 x - sin2 x]
= 2a [cos 4t + cos 2t]
y = b cos 2t (1 - cos 2t)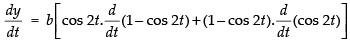
= b [cos 2t. sin 2t.2 + (1- cos 2t ).( - sin 2t ).2]
= b [2 sin 2t. cos 2t - 2 sin 2t+ 2 sin 2t cos 2t]
= b [sin 4t - 2 sin 2t+ sin 4t] [∵ sin 2x = 2 sin x cos x]
= b [2 sin 4t - 2 sin 2t ] = 2b (sin 4t – sin 2t)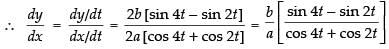
Put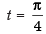
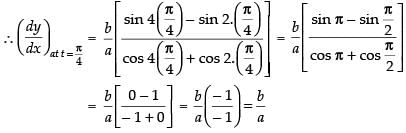
Hence,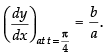
Q.51. If x = 3sint – sin 3t, y = 3cost – cos 3t, find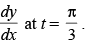
Ans.
Given that: x = 3 sin t – sin 3t, y = 3 cos t – cos 3t.
Differentiating both parametric functions w.r.t. t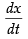 = 3 cos t – cos 3t.3 = 3(cos t – cos 3t)
= 3 cos t – cos 3t.3 = 3(cos t – cos 3t)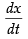 = – 3 sin t + sin 3t.3 = 3(– sin t + sin 3t)
= – 3 sin t + sin 3t.3 = 3(– sin t + sin 3t)
∴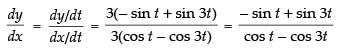
Put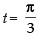
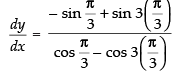
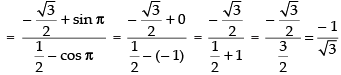
Hence,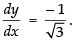
Q.52. Differentiate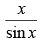 w.r.t. sinx.
w.r.t. sinx.
Ans.
Let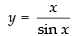 and z = sin x.
and z = sin x.
Differentiating both the parametric functions w.r.t. x,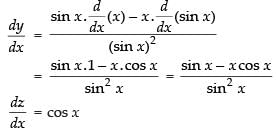
∴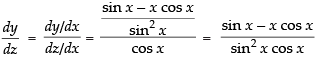
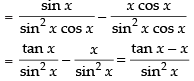
Hence,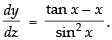
Q.53. Differentiate tan–1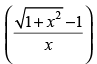 w.r.t. tan–1 x when x ≠ 0.
w.r.t. tan–1 x when x ≠ 0.
Ans.
Let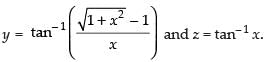
Put x = tan θ.
∴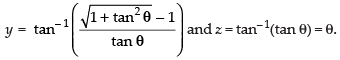
⇒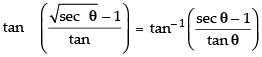
⇒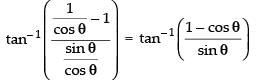
⇒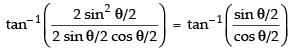
⇒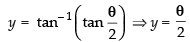
Differentiating both parametric functions w.r.t. θ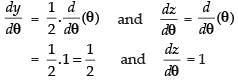
∴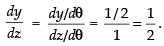
Find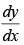 when x and y are connected by the relation given in each of the Exercises 54 to 57.
when x and y are connected by the relation given in each of the Exercises 54 to 57.
Q.54.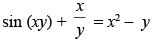
Ans.
Given that: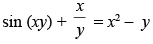
Differentiating both sides w.r.t. x
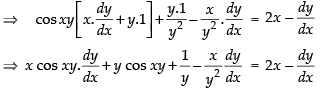
⇒
⇒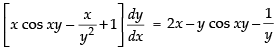
⇒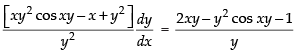
⇒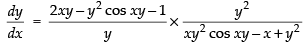
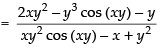
Hence,
Q.55. sec (x + y) = xy
Ans.
Given that: sec (x + y) = xy
Differentiating both sides w.r.t. x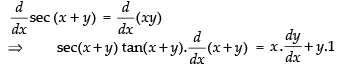

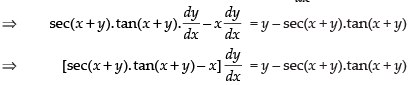
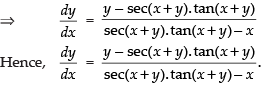
Q.56. tan–1 (x2 + y2) = a
Ans.
Given that: tan– 1(x2 + y2) = a
⇒ x2 + y2 = tan a.
Differentiating both sides w.r.t. x.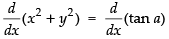
⇒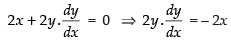
⇒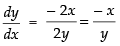
Hence,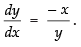
Q.57. (x2 + y2)2 = xy
Ans.
Given that: (x2 + y2)2 = xy
⇒ x4 + y4 + 2x2y2 = xy
Differentiating both sides w.r.t. x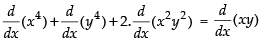
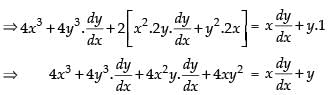
⇒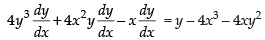
⇒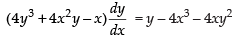
⇒
Hence,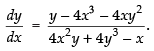
Q.58. If ax2 + 2hxy + by2 + 2gx + 2fy + c = 0, then show that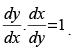
Ans.
Given that: ax2 + 2hxy + by2 + 2gx + 2fy + c = 0.
Differentiating both sides w.r.t. x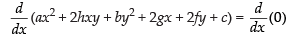
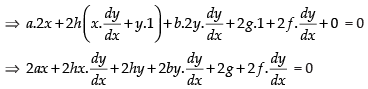
⇒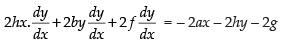
⇒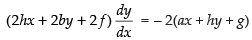
⇒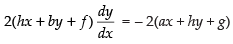
⇒
⇒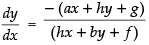
Now, differentiating the given equation w.r.t. y.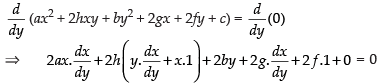
⇒
⇒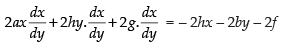
⇒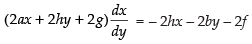
⇒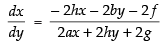
⇒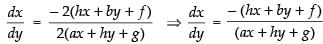
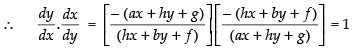
Hence,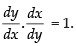 Hence, proved.
Hence, proved.
Q.59. If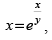 prove that
prove that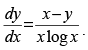
Ans.
Given that: x = ex/y
Taking log on both the sides,
log x = log ex/y
⇒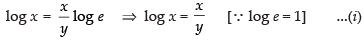
Differentiating both sides w.r.t. x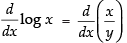
⇒
⇒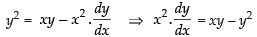
⇒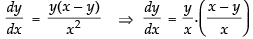
⇒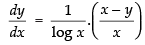
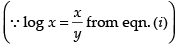
Hence,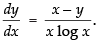
Q.60. If yx = ey − x , prove that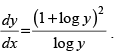
Ans.
Given that: yx = ey – x
Taking log on both sides log yx = log ey – x
⇒x log y = (y – x) log e
⇒ x log y = y – x [∵ log e = 1]
⇒ x log y + x = y
⇒ x (log y + 1) = y
⇒
Differentiating both sides w.r.t. y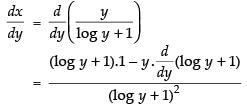
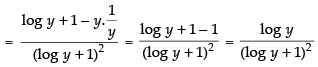
We know that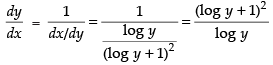
Hence,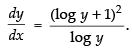
Q.61. If 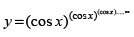 , show that
, show that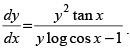
Ans.
Given that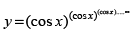
⇒ y = (cos x)y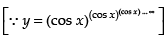
Taking log on both sides log y = y.log (cos x)
Differentiating both sides w.r.t. x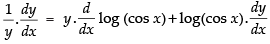
⇒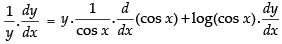
⇒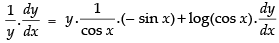
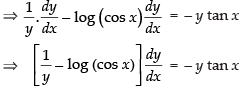
⇒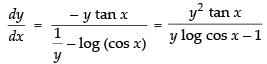
Hence,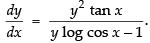 Hence, proved.
Hence, proved.
Q.62. If x sin (a + y) + sin a cos (a + y) = 0, prove that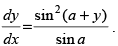
Ans.
Given that: x sin (a + y) + sin a cos (a + y) = 0
⇒ x sin (a + y) = – sin a cos (a + y)
⇒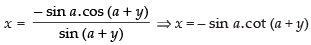
Differentiating both sides w.r.t. y
⇒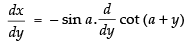
⇒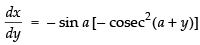
⇒
∴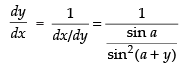
Hence,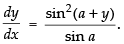 Hence proved.
Hence proved.
Q.63. If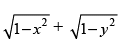 = a (x – y), prove that
= a (x – y), prove that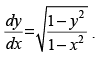
Ans.
Given that: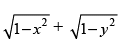 = a (x – y)
= a (x – y)
Put x = sin θ and y = sin ϕ.
∴ θ = sin– 1 x and ϕ = sin– 1 y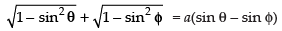
⇒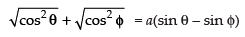
⇒ cos θ + cos ϕ = a(sin θ – sin ϕ)
⇒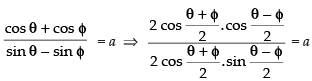
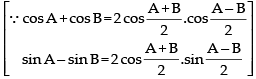
⇒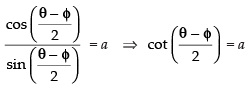
⇒
⇒ sin– 1 x – sin– 1 y = 2 cot– 1 a
Differentiating both sides w.r.t. x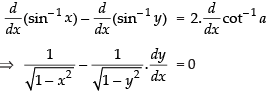
⇒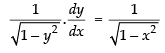
∴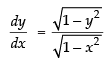
Hence,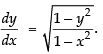
Q.64. If y = tan–1x, find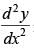 in terms of y alone.
in terms of y alone.
Ans.
Given that: y = tan– 1 x ⇒ x = tan y
Differentiating both sides w.r.t. y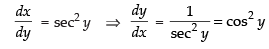
Again differentiating both sides w.r.t. x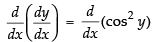
⇒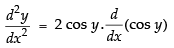
⇒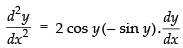
⇒
∴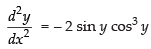
|
172 videos|487 docs|154 tests
|
FAQs on NCERT Exemplar: Continuity and Differentiability- 1 - Mathematics (Maths) for JEE Main & Advanced
| 1. What is the definition of continuity in mathematics? |  |
| 2. How can we determine if a function is continuous at a given point? |  |
| 3. What is the difference between continuity and differentiability? |  |
| 4. How can we determine if a function is differentiable at a given point? |  |
| 5. Can a function be differentiable but not continuous? |  |
















