NCERT Exemplar: Continuity and Differentiability- 2 | Mathematics (Maths) Class 12 - JEE PDF Download

Verify the Rolle’s theorem for each of the functions in Exercises 65 to 69.
Q.65. f (x) = x (x – 1)² in [0, 1].
Ans.
Given that: f(x) = x(x – 1)² in [0, 1]
(i) f(x) = x(x – 1)², being an algebraic polynomial, is continuous in [0, 1].
(ii) f ′(x) = x.2 (x - 1) + (x - 1)².1
= 2x² - 2x + x² + 1 - 2x
= 3x² - 4x + 1 which exists in (0, 1)
(iii) f(x) = x(x – 1)² 
f(0) = 0(0 – 1)² = 0; f(1) = 1(1 – 1)² = 0
⇒ f(0) = f(1) = 0
As the above conditions are satisfied, then there must exist at least one point c ∈ (0, 1) such that f ′(c) = 0
∴ f ′(c) = 3c² - 4c + 1 = 0 ⇒ 3c² - 3c - c + 1 = 0
⇒ 3c(c - 1) - 1(c - 1) = 0 ⇒ (c - 1)(3c - 1) = 0
⇒ c – 1 = 0 ⇒ c = 1
3c – 1 = 0 ⇒ 3c = 1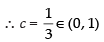
Hence, Rolle’s Theorem is verified.

Q.66. f (x) = sin⁴x + cos⁴x in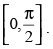
Ans.
Given that: f (x) = sin⁴x + cos⁴x in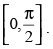
(i) f(x) = sin⁴ x + cos⁴ x, being sine and cosine functions, f(x) is
continuous function in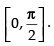
(ii) f ′(x) = 4 sin³ x.cos x + 4 cos³ x (- sin x)
= 4 sin³ x.cos x - 4 cos³ x.sin x
= 4 sin x cos x (sin² x – cos² x)
= – 4 sin x cos x (cos² x – sin² x)
= – 2.2 sin x cos x.cos 2x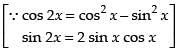
= – 2 sin 2x.cos 2x
= – sin 4x which exists in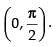
So, f (x) is differentiable in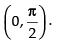

Q.67. f (x) = log (x² + 2) – log3 in [–1, 1].
Ans.
Given that: f(x) = log (x² + 2) – log 3 in [– 1, 1]
(i) f(x) = log (x² + 2) – log 3, being a logarithm function, is continuous in [– 1, 1].
(ii) f ′(x) =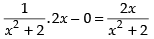which exists in (– 1, 1)
So, f (x) is differentiable in (– 1, 1).
(iii) f(– 1) = log (1 + 2) – log 3 ⇒ log 3 - log 3 = 0
f(1) = log (1 + 2) - log 3 ⇒ log 3 - log 3 = 0
∴ f(- 1) = f(1) = 0
As the above conditions are satisfied, then there must exist atleast one point c ∈ (- 1, 1) such that f ′(c) = 0.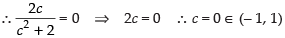

Hence, Rolle’s Theorem is verified.

Q.68. f (x) = x (x + 3)e^–x/2 in [–3, 0].
Ans.
Given that: f(x) = x(x + 3) e^{– x/2} in [– 3, 0]
(i) Algebraic functions and exponential functions are continuous in their domains.
∴ f(x) is continuous in [– 3, 0]
(ii) f ′(x) =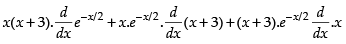


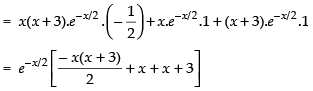
So, f (x) is differentiable in (– 3, 0).
(iii) f(– 3) = (– 3) (– 3 + 3) e^{– 3/2} = 0
f(0) = (0) (0 + 3) e^{– 0/2} = 0
∴ f(– 3) = f(0) = 0
As the above conditions are satisfied, then there must exist
atleast one point c ∈ (- 3, 0) such that
f ′(c) = 0⇒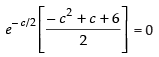

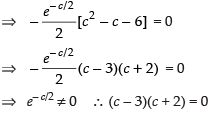
Which gives c = 3, c = – 2 ∈ (- 3, 0).
Hence, Rolle’s Theorem is verified.

Q.69. f (x) =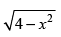in [– 2, 2].
Ans.
Given that: f (x) =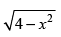in [– 2, 2].
(i) Since algebraic polynomials are continuous,
∴ f(x) is continuous in [– 2, 2]
(ii) f ′(x) =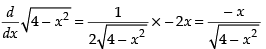which exists in (– 2, 2)
So, f  ′(x) is differentiable in (- 2, 2).
(iii)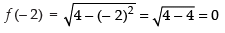

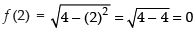
So f (– 2) = f (2) = 0
As the above conditions are satisfied, then there must exist
atleast one point c ∈ (- 2, 2) such that
f ′(c) = 0⇒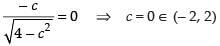
Hence, Rolle’s Theorem is verified.

Q.70. Discuss the applicability of Rolle’s theorem on the function given by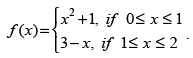

Ans.
(i) f(x) being an algebraic polynomial, is continuous everywhere.
(ii) f(x) must be differentiable at x = 1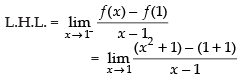


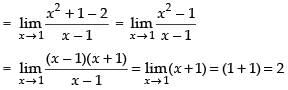
and R.H.L. =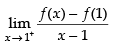

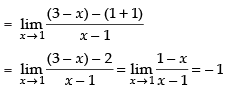
∴ L.H.L. ≠ R.H.L.
So, f(x) is not differentiable at x = 1.
Hence, Rolle’s Theorem is not applicable in [0, 2].

Q.71. Find the points on the curve y = (cosx – 1) in [0, 2π], where the tangent is parallel to x-axis.
Ans.
Given that: y = cos x – 1 on [0, 2π]
We have to find a point c on the given curve y = cos x – 1 on [0, 2π] such that the tangent at c ∈ [0, 2π] is parallel to x-axis i.e., f ′(c) = 0 where f ′(c) is the slope of the tangent.
So, we have to verify the Rolle’s Theorem.
(i) y = cos x – 1 is the combination of cosine and constant functions.
So, it is continuous on [0, 2π].
(ii)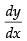= – sin x which exists in (0, 2π).
So, it is differentiable on (0, 2π).
(iii) Let f(x) = cos x – 1
f(0) = cos 0 – 1 = 1 – 1 = 0; f(2π) = cos 2π – 1 = 1 – 1 = 0
∴ f(0) = f(2π) = 0
As the above conditions are satisfied, then there lies a point
c ∈ (0, 2π) such that f ′(c) = 0.
∴ - sin c = 0 ⇒ sin c = 0
∴ c = nπ, n ∈ I
⇒ c = π ∈ (0, 2π)
Hence, c = π is the point on the curve in (0, 2π) at which the tangent is parallel to x-axis.

Q.72. Using Rolle’s theorem, find the point on the curve y = x (x – 4), x ∈ [0, 4], where the tangent is parallel to x-axis.
Ans.
Given that: y = x(x – 4), x ∈ [0, 4]
Let f(x) = x(x - 4), x ∈ [0, 4]
(i) f(x) being an algebraic polynomial, is continuous function everywhere.
So, f(x) = x(x – 4) is continuous in [0, 4].
(ii) f ′(x) = 2x - 4 which exists in (0, 4).
So, f (x) is differentiable.
(iii) f(0) = 0(0 – 4)
= 0 f(4) = 4(4 – 4) = 0
So f(0) = f(4) = 0
As the above conditions are satisfied, then there must exist at least one point c ∈ (0, 4) such that f ′(c) = 0
∴ 2c - 4 = 0 ⇒ c = 2 ∈ (0, 4)
Hence, c  = 2 is the point in (0, 4) on the given curve at which the tangent is parallel to the x-axis.

Verify mean value theorem for each of the functions given Exercises 73 to 76.
Q.73.  f (x) =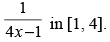
Ans.
Given that: f (x) =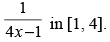
(i) f(x) is an algebraic function, so it is continuous in [1, 4].
(ii) f ′(x) =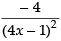
So, f (x) is differentiable.
As the above conditions are satisfied then there must exist a point
c ∈ (1, 4) such that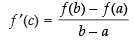



∴
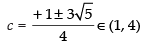
Hence, Mean Value Theorem is verified.

Q.74. f (x) = x³ – 2x² – x + 3 in [0, 1].
Ans.
Given that: f(x) = x³ – 2x² – x + 3 in [0, 1]
(i) Being an algebraic polynomial, f(x) is continuous in [0, 1]
(ii) f ′(x) = 3x² - 4x - 1 which exists in (0, 1).
So, f (x) is differentiable.
As the above conditions are satisfied, then there must exist atleast one point c ∈ (0, 1) such that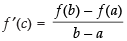

⇒
⇒
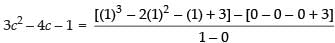
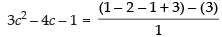
⇒ 3c² – 4c – 1 = 1 – 3  ⇒ 3c² - 4c - 1 = -2
⇒ 3c² - 4c + 1 = 0  ⇒ 3c² - 3c - c + 1 = 0
⇒ 3c (c - 1) -1 (c - 1) = 0  ⇒ (c - 1) (3c - 1) = 0
⇒ c – 1 = 0 ∴ c = 1
3c – 1 = 0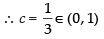
Hence, Mean Value Theorem is verified.

Q.75. f (x) = sinx – sin2x in [0, π].
Ans.
Given that: f(x) = sin x – sin 2x in [0, π]
(i) Since trigonometric functions are always continuous on their domain.
So, f (x) is continuous on [0, π].
(ii) f ′(x) = cos x - 2 cos 2x which exists in (0, π)
So, f (x) is differentiable on (0, π).
Since the above conditions are satisfied, then there must exist atleast one point c ∈ (0, π) such that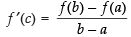

cos c – 2 cos 2c =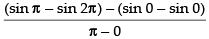
⇒ cos c – 2(2 cos² c – 1) = 0 ⇒ cos c - 4 cos² c + 2 = 0
⇒ 4 cos² c - cos c - 2 = 0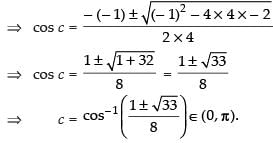

Hence, Mean Value Theorem is verified.

Q.76. f (x) =in [1, 5].
Ans.
Given that: f (x) =in [1, 5].
(i) f(x) is continuous if 25 – x² ≥ 0 ⇒ - x² ≥ - 25
⇒ x² ≤ 25 ⇒ x ≤ ± 5 ≤ - 5 ≤ x ≤ 5
So, f (x) is continuous on [1, 5].
(ii) f ′(x)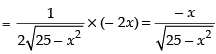which exists in (1, 5).
So, f (x) is differentiable in [1, 5].
Since the above conditions are satisfied then there must exist atleast one point c ∈ (1, 5) such that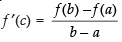



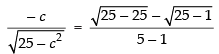
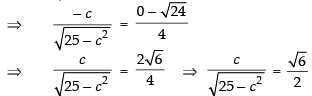
Squaring both sides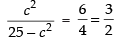

⇒ 2c² = 75 – 3c² ⇒ 5c² = 75  ⇒ c² = 15
∴ c = ± √15 ∈ (1, 5)
Hence, Mean Value Theorem is verified.

Q.77. Find a point on the curve y = (x – 3)², where the tangent is parallel to the chord joining the points (3, 0) and (4, 1).
Ans.
Given that: y = (x – 3)² 
Let f(x) = (x – 3)² 
(i) Being an algebraic polynomial, f(x) is continuous at x₁ = 3 and x₂ = 4 i.e. in [3, 4].
(ii) f ′(x) = 2(x - 3) which exists in (3, 4).
Hence, by mean value theorem, there must exist a point c on the curve at which the tangent is parallel to the chord joining the points (3, 0) and (4, 1).
∴

∴
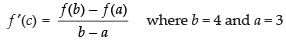
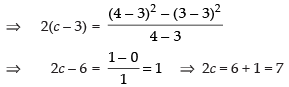
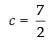
If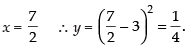
Hence,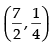is the point on the curve at which the tangent is
parallel to the chord joining the points (3, 0) and (4, 1)

Q.78. Using mean value theorem, prove that there is a point on the curve y = 2x² – 5x + 3 between the points A(1, 0) and B (2, 1), where tangent is parallel to the chord AB. Also, find that point.
Ans.
Given that: y = 2x² – 5x + 3
Let f(x) = 2x² – 5x + 3
(i) Being an algebraic polynomial, f(x) is continuous in [1, 2].
(ii) f ′(x) = 4x - 5 which exists in (1, 2).
As per the Mean Value Theorem, there must exist a point
c ∈ (1, 2) on the curve at which the tangent is parallel to the chord joining the
points A(1, 0) and B(2, 1).
So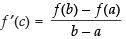

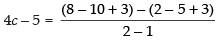
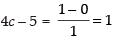⇒⇒ 4c = 1 + 5 ⇒ 4c = 6
∴
∴

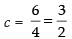
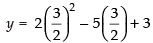
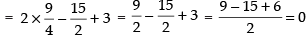
Hence,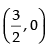is the point on the curve at which the tangent is
parallel to the chord joining the points A(1, 0) and B(2, 1).

Long Answer (L.A.)
Q.79. Find the values of p and q so that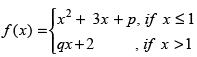

Ans.
Given that: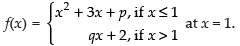

L.H.L.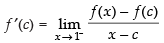
⇒


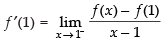
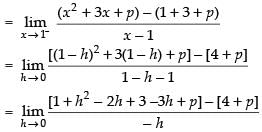
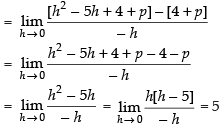
R.H.L.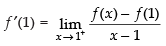

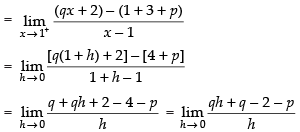
For existing the limit
q – 2 – p = 0 ⇒ q – p = 2 ...(i)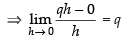

If L.H.L. f ′(1) = R.H.L. f ′(1) then q = 5.
Now putting the value of q in eqn. (i)
5 – p = 2 ⇒ p = 3.
Hence, value of p is 3 and that of q is 5.

Q.80. If x^m.yⁿ = (x + y)^m+n, prove that
(i)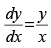and
(ii)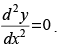
Ans.
(i) Given that: x^m.yⁿ = (x + y)^{m + n}
Taking log on both sides
log x^m.yⁿ = log (x + y)^{m + n} [∵ log xy = log x + log y]
⇒ log x^m + log yⁿ = (m + n) log (x + y)
⇒ m log x + n log y = (m + n) log (x + y)
Differentiating both sides w.r.t. x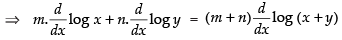

⇒
⇒
⇒
⇒
⇒

⇒
⇒
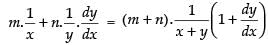
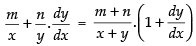
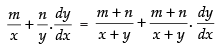
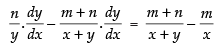
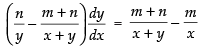
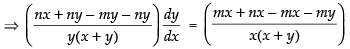
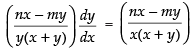
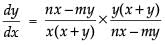
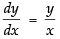⇒Hence proved.

(ii) Given that: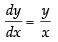
 Differentiating both sides w.r.t. x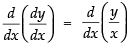

⇒

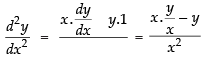
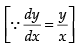
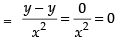
Hence,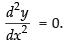Hence, proved.

Q.81. If x = sint and y = sin pt, prove that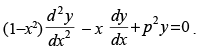

Ans.
Given that: x = sin t and y = sin pt
Differentiating both the parametric functions w.r.t.t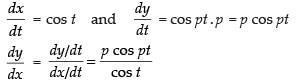

∴
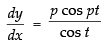
Again differentiating w.r.t. x,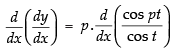

⇒

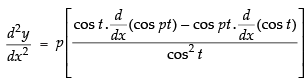
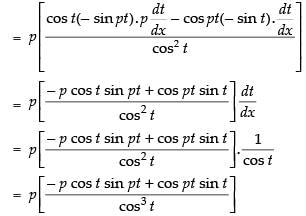
Now we have to prove that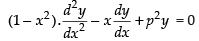


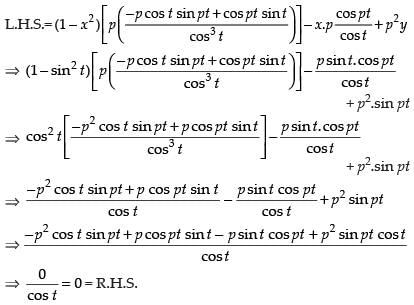
Hence, proved.

Q.82. Find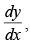 if y = x^tanx +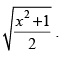
Ans.
Given that: y =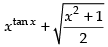
Let u = x^tanx and v =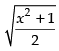
∴ y = u + v
Differentiating both sides w.r.t. x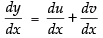
...(i)

Now taking u = x^{tan x} 
Taking log on both sides log u = log (x^{tan x})
log u = tan x . log x
Differentiating both sides w.r.t. x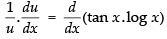


⇒
∴
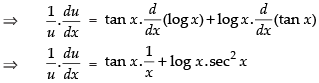
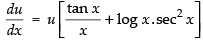
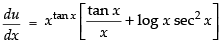
Taking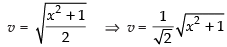
Differentiating both sides w.r.t. x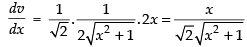

Putting the values of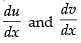in eqn. (i)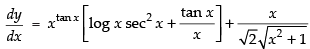


Objective Type Questions
Q.83. If f (x) = 2x and g (x) =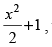then which of the following can
be a discontinuous function
(a) f(x) + g(x) 
(b) f(x) – g(x) 
(c) f(x).g(x) 
(d)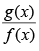
Ans. (d)
Solution.
We know that the algebraic polynomials are continuous functions everywhere.
∴ f(x) + g(x) is continuous [∵ Sum, difference and product
f(x) - g(x) is continuous of two continuous functions is
f(x) . g(x) is continuous also continuous]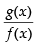
 is only continuous if g(x) ≠ 0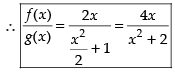

Here,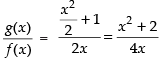which is discontinuous at x = 0.
Hence, the correct option is (d).

Q.84. The function f (x) =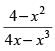is
(a) discontinuous at only one point 
(b) discontinuous at exactly two points 
(c) discontinuous at exactly three points 
(d) none of these
Ans. (c)
Solution.
Given that: f(x) =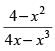
For discontinuous function  4x – x³ = 0
⇒ x(4 – x²) = 0
⇒ x(2 – x)(2 + x) = 0
⇒ x = 0, x = – 2, x = 2
Hence, the given function is discontinuous exactly at three points.
Hence, the correct option is (c).

Q.85. The set of points where the function f given by f(x) = 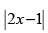 sinx is differentiable is
(a) R 
(b)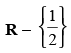
(C) (0, ∞) 
(D) none of these
Ans. (b)
Solution.
Given that: f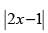(x) =sinx
Clearly, f(x) is not differentiable at x =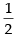
R.H.L. =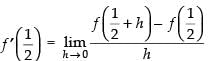

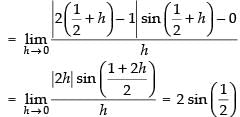
Also L.H.L. =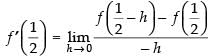

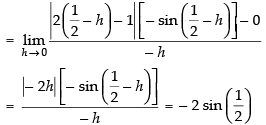
∴ R.H.L. =
So, the given function f(x) is not differentiable at x =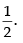
∴ f(x) is differentiable in R -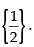
Hence, the correct option is (b).

Q.86. The function f (x) = cot x is discontinuous on the set
(a) {x = nπ; n ∈ Z} 
(b) {x = 2nπ; n ∈ Z}
(c)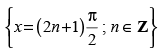
(d)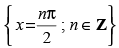
Ans. (a)
Solution.
Given that: f(x) = cot x
⇒
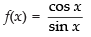
We know that sin x = 0 if f(x) is discontinuous.
∴ If sin x = 0
∴ x = nπ, n ∈ nπ.
So, the given function f(x) is discontinuous on the set {x = nπ; n ∈ Z}.
Hence, the correct option is (a).

Q.87. The function f (x) =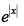is
(a) continuous everywhere but not differentiable at x = 0 
(b) continuous and differentiable everywhere. 
(c) Not continuous at x = 0 
(d) None of these
Ans. (a)
Solution.
Given that: f(x) =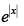 
We know that modulus function is continuous but not differentiable in its domain.
Let g(x) = 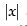 and t(x) = e^x
∴ f(x) = got(x) = g[t(x)] =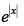 
Since g (x) and t(x) both are continuous at x = 0 but f(x) is not differentiable at x = 0.
Hence, the correct option is (a).

Q.88. If f (x) = x² sin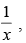 where x ≠ 0, then the value of the function f at x = 0, so that the function is continuous at x = 0, is
(a) 0 
(b) – 1 
(c) 1 
(d) none of these
Ans. (a)
Solution.
Given that: f(x) = x² sinwhere x ≠ 0.
So, the value of the function f at x = 0, so that f(x) is continuous is 0.
Hence, the correct option is (a).

Q.89. If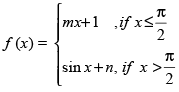 , is continuous at x =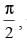then
(a) m = 1, n = 0 
(b)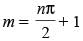
(c)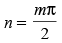
(d) m = n=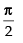
Ans. (c)
Solution.
Given that: f(x) =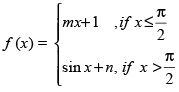 is continuous at x =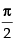
L.H.L. ==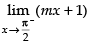
R.H.L. =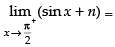

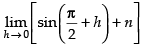
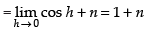
When f(x) is continuous at x =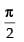
∴ L.H.L. = R.H.L.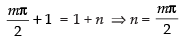

Hence, the correct option is (c).

Q.90. Let f (x) = |sin x|. Then
(a) f  is everywhere differentiable
(b) f  is everywhere continuous but not differentiable at x = nπ, n ∈ Z.
(c) f  is everywhere continuous but not differentiable at x = (2n + 1)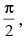
 n ∈ Z.
(d) none of these
Ans. (b)
Solution.
Given that: f(x) =|sin x|
Let g(x) = sin x and t(x) =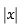
∴ f(x) = tog(x) = t[g(x)] = t(sin x) =|sin x|
where g(x) and  t(x) both are continuous.
∴ f(x) = got(x) is continuous but t(x) is not differentiable at x = 0.
So, f(x) is not continuous at sin x = 0 ⇒ x = nπ, n ∈ Z.
Hence, the correct option is (b).

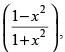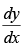Q.91. If y = logthenis equal to
(a)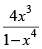
(b)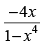
(c)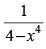
(d)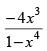
Ans. (b)
Solution.
Given that: y =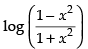
⇒ y = log (1 – x²) – log (1 + x²)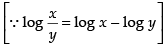
Differentiating both sides w.r.t. x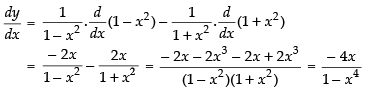

Hence, the correct option is (b).

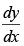Q.92. If y =thenis equal to
(a)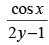
(b)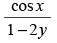
(c)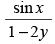
(d)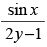
Ans. (a)
Solution.
Given that: y =
Differentiating both sides w.r.t. x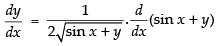

⇒
⇒
⇒
⇒
⇒
⇒
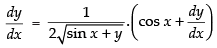
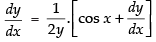
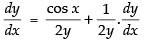
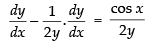
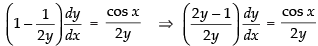
Hence, the correct option is (a).

Q.93. The derivative of cos–1 (2x² – 1) w.r.t. cos^–1x is
(a) 2 
(b)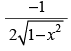
(c)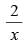
(d) 1 – x²
Ans. (a)
Solution.
Let y = cos^{– 1}(2x² – 1) and t = cos^{– 1} x
Differentiating both the functions w.r.t. x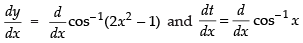

⇒

⇒
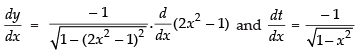
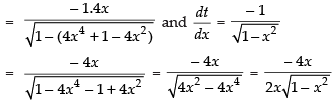
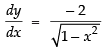
Now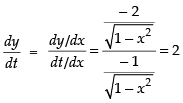
Hence, the correct option is (a).

Q.94. If x = t², y = t³, then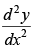 is
(a) 3/2
(b) 3/4t
(c) 3/2t
(d)2/3t
Ans. (b)
Solution.
Given that x = t² and y = t³ 
Differentiating both the parametric functions w.r.t. t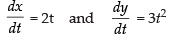

∴
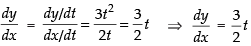
Now differentiating again w.r.t. x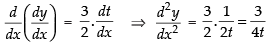

Hence, the correct option is (b).

Q.95. The value of c in Rolle’s theorem for the function f (x) = x³ – 3x in the interval [0, √3 ] is
(a) 1
(b) – 1
(c) 3/2
(d) 1/3
Ans. (a)
Solution.
Given that: f(x) = x³ – 3x in [0 , √3 ]
We know that if f(x) = x³ – 3x satisfies the conditions of Rolle’s
Theorem in [0 , √3 ] , then
f ′(c) = 0
⇒ 3c² - 3 = 0  ⇒ 3c²  = 3 ⇒ c² = 1
∴ c = ± 1 ⇒ 1 ∈ (0, √3 )
Hence, the correct option is (a).

Q.96. For the function f (x) = x +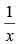, x ∈ [1, 3], the value of c for mean value theorem is
(a) 1 
(b) √3 
(c) 2 
(d) none of these
Ans. (b)
Solution.
Given that: f (x) = x +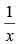, x ∈ [1, 3]
We know that if f(x) = x +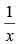, x ∈ [1, 3] satisfies all the
conditions of mean value theorem then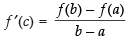
where a = 1 and b = 3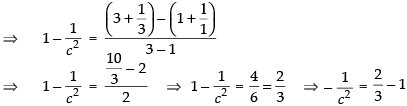


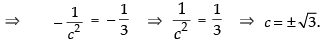
Here c = √3 ∈ (1, 3).
Hence, the correct option is (b).

Fill in the blanks
Q.97. An example of a function which is continuous everywhere but fails to be differentiable exactly at  two points is _________.
Ans.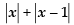
is the function which is continuous everywhere
but fails to be differentiable at x = 0 and x = 1.
We can have more such examples.

Q.98. Derivative of x² w.r.t. x³ is _________.
Ans.
Let y  = x² and t = x³ 
Differentiating both the parametric functions w.r.t. x⇒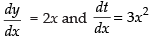

∴
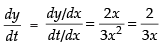
So, the derivative of x² w.r.t. x³ is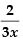

Q.99. If f (x) = |cosx|, then f ′= _______ .
Ans.
Given that: f (x) = |cosx|
⇒ f(x) = cos x if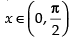
Differentiating both sides w.r.t. x, we get f ′(x) = - sin x
at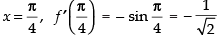

Q.100. If f (x) = |cosx – sinx | , then f ′= _______.
Ans.
Given that: f (x) = |cosx – sinx |
We know that sin x > cos x if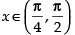
⇒ cos x – sin x < 0
∴ f(x) = – (cos x – sin x)
f ′(x) = - (- sin x - cos x) ⇒ f ′(x) = (sin x + cos x)
∴

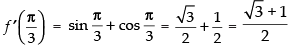
Q.101. For the curve √x + √y = 1 ,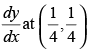is ________.
Ans.
Given that: √x + √y = 1
Differentiating both sides w.r.t. x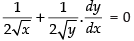

⇒
⇒
∴

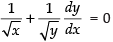
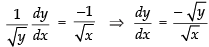
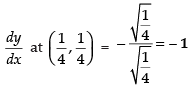
State True or False for the statements
Q.102. Rolle’s theorem is applicable for the function f (x) = |x – 1| in [0, 2].
Ans.
False. Given that f(x) =|x – 1| in [0, 2].
We know that modulus function is not differentiable. So, it is false.

Q.103. If f is continuous on its domain D, then | f | is also continuous on D.
Ans.
True. We know that modulus function is continuous function on its domain.
So, it is true.

Q.104. The composition of two continuous function is a continuous function.
Ans.
True. We know that the sum and difference of two or more functions is always continuous. So, it is true.

Q.105. Trigonometric and inverse - trigonometric functions are differentiable in their respective domain.
Ans.
True.

Q.106. If f  . g  is continuous at x = a, then f and g are separately continuous at x = a.
Ans.
False. Let us take an example: f(x) = sin x and g(x) = cot x
∴ f(x).g(x) = sin x.cot x =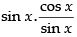= cos x which is continuous at x = 0
but cot x is not continuous at x = 0.