NCERT Exemplar: Differential Equations | Mathematics (Maths) for JEE Main & Advanced PDF Download
Short Answer Type Questions
Q.1. Find the solution of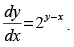
Ans.
The given differential equation is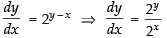
Separating the variables, we get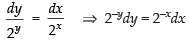
Integrating both sides, we get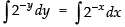
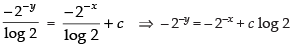
⇒ – 2–y + 2–x = c log 2
⇒ 2–x – 2–y = k [where c log 2 = k]
Q.2. Find the differential equation of all non vertical lines in a plane.
Ans.
Equation of all non vertical lines are y = mx + c
Differentiating with respect to x, we get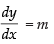
Again differentiating w.r.t. x we have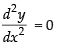
Hence, the required equation is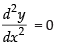
Q.3. Given that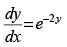 and y = 0 when x = 5. Find the value of x when y = 3.
and y = 0 when x = 5. Find the value of x when y = 3.
Ans.
Given equation is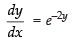
⇒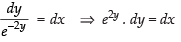
Integrating both sides, we get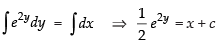
Put y = 0 and x = 5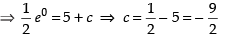
∴ The equation becomes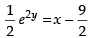
Now putting y = 3, we get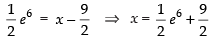
Hence the required value of x =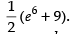
Q.4. Solve the differential equation (x2 – 1)
Ans.
Given differential equation is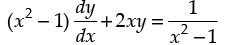
Dividing by (x2 – 1), we get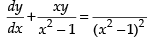
It is a linear differential equation of first order and first degree.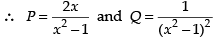
Integrating factor I.F. =
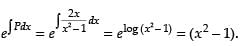
∴ Solution of the equation is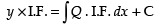
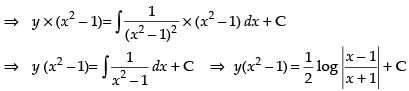
Hence the required solution is 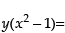
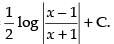
Q.5. Solve the differential equation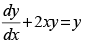
Ans.
Given equation is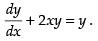
⇒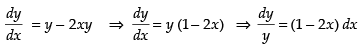
Integrating both sides, we have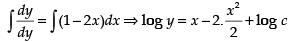
⇒ log y = x – x2 + log c
⇒ log y – log c = x – x2
⇒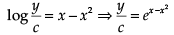
∴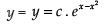
Hence, the required solution is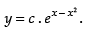
Q.6. Find the general solution of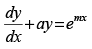
Ans.
Given equation is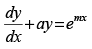
Here, P = a and Q = emx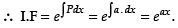
Solution of equation is y x I.F =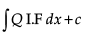
⇒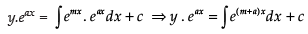
⇒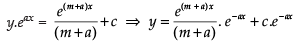
∴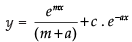
Hence the required solution is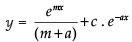
Q.7. Solve the differential equation
Ans.
Given that: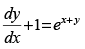
Put x + y = t
∴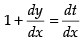
∴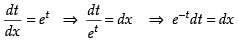
Integrating both sides, we have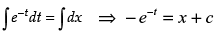
⇒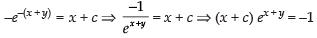
Hence, the required solution is ( x + c) . e xy + 1= 0.
Q.8. Solve: ydx – xdy = x2ydx.
Ans.
Given equation is ydx – xdy = x2y dx.
⇒ y dx - x2y dx = xdy
⇒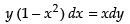
⇒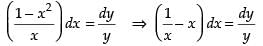
Integrating both sides we get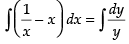
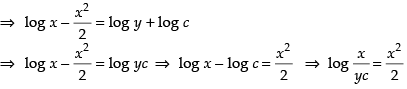
⇒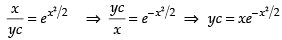
∴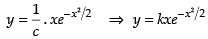
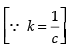
Hence, the required solution is y =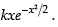
Q.9. Solve the differential equation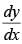 = 1 + x + y2 + xy2, when y = 0, x = 0.
= 1 + x + y2 + xy2, when y = 0, x = 0.
Ans.
Given equation is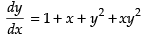
⇒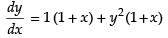
⇒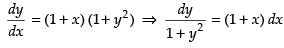
Integrating both sides, we get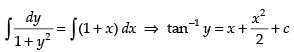
Put x = 0 and y = 0, we get tan–1(0) = 0 + 0 + c
⇒ c = 0
∴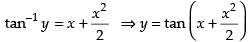
Hence, the required solution is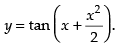
Q.10. Find the general solution of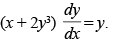
Ans.
Given equation is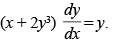
⇒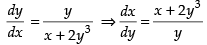
⇒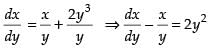
Here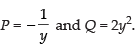
∴ Integrating factor I.F. =
So the solution of the equation is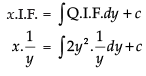
⇒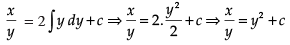
So x = y3 + cy = y(y2 + c)
Hence, the required solution is x = y (y2 + c).
Q.11. If y(x) is a solution of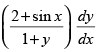 = – cos x and y (0) = 1, then find the value of
= – cos x and y (0) = 1, then find the value of
Ans.
Given equation is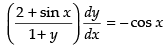
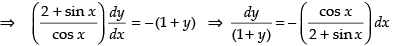
Integrating both sides, we get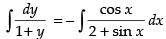
⇒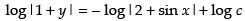

⇒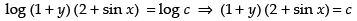
Put x = 0 and y = 1, we get
(1 + 1) (2 + sin 0) = c ⇒ 4 = c
∴ equation is (1 + y) (2 + sin x) = 4
Now put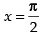
∴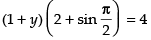
⇒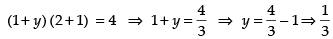
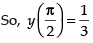
Hence, the required solution is
Q.12. If y(t) is a solution of (1 + t)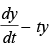 and y (0) = – 1, then show that
and y (0) = – 1, then show that
y (1) =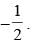
Ans.
Given equation is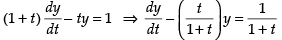
Here,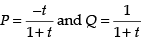
∴ Integrating factor I.F.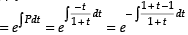
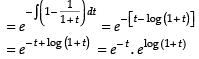
∴ I.F. = e–t . (1 + t)
Required solution of the given differential equation is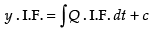
⇒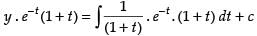
⇒
⇒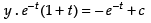
Put t = 0 and y = –1 [∵ y(0) = –1]
⇒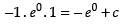
⇒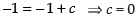
So the equation becomes
ye–t (1 + t) = –e–t
Now put t = 1
∴ y . e–1 (1 + 1) = –e–1
⇒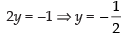
Hence y (1) =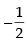 is verified.
is verified.
Q.13. Form the differential equation having y = (sin–1x)2 + Acos–1x + B, where A and B are arbitrary constants, as its general solution.
Ans.
Given equation is y = (sin–1x)2 + A cos–1x + B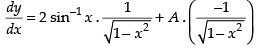
Multiplying both sides by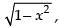 we get
we get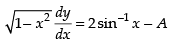
Again differentiating w.r.t x, we get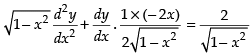 ⇒
⇒
⇒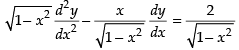
Multiplying both sides by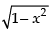 , we get
, we get
⇒
Which is the required differential equation.
Q.14. Form the differential equation of all circles which pass through origin and whose centres lie on y-axis.
Ans.
Equation of circle which passes through the origin and whose centre lies on y-axis is
(x – 0)2 + (y – a)2 = a2
⇒ x2 + y2 + a2 – 2ay = a2
⇒ x2 + y2 – 2ay = 0 ...(i)
Differentiating both sides w.r.t. x we get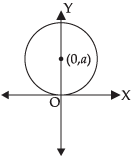
⇒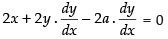
⇒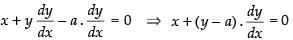
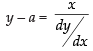
∴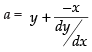
Putting the value of a in eq. (i), we get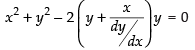
⇒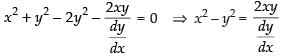
∴
Hence, the required differential equation is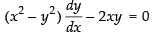
Q.15. Find the equation of a curve passing through origin and satisfying the differential equation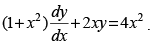
Ans.
Given equation is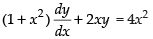
⇒
Here,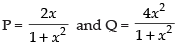
Integrating factor I.F. =
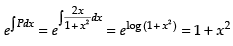
∴ Solution is
⇒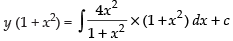
⇒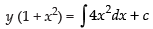
⇒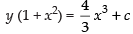 ...(i)
...(i)
Since the curve is passing through origin i.e., (0, 0)
∴ Put y = 0 and x = 0 in eq. (i)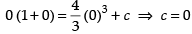
∴ Equation is
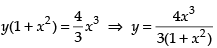
Hence, the required solution is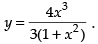
Q.16. Solve :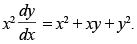
Ans.
Given equation is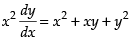
⇒
Put y = vx [∵ it is a homogeneous differential equation]
∴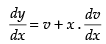
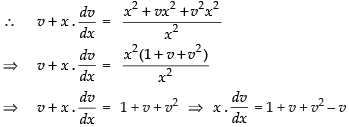
⇒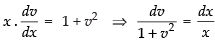
Integrating both sides, we get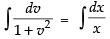
⇒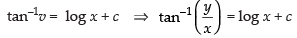
Hence, the required solution is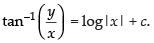
Q.17. Find the general solution of the differential equation (1 + y2) +
(x – etan–1y)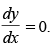
Ans.
Given equation is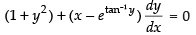
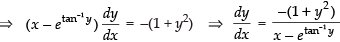
⇒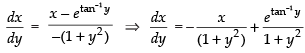
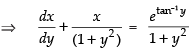
Here,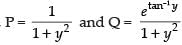
∴ Integrating factor I.F. =
∴ Solution is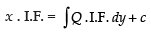
⇒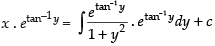
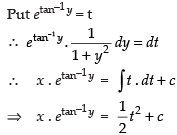
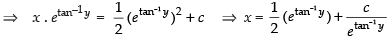
⇒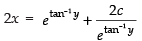
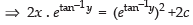
Hence, this is the required general solution.
Q.18. Find the general solution of y2dx + (x2 – xy + y2) dy = 0.
Ans.
The given equation is y2 dx + ( x2 - xy+ y2 ) dy =0 .
⇒ y2dx = – (x2 – xy + y2) dy
⇒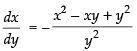
Since it is a homogeneous differential equation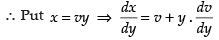
So,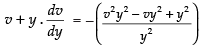
⇒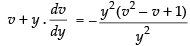
⇒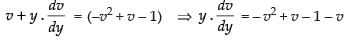
⇒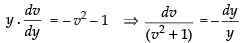
Integrating both sides, we get
⇒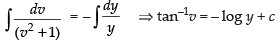
⇒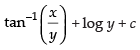
Hence the required solution is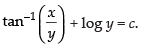
Q.19. Solve: (x + y) (dx – dy) = dx + dy. [Hint: Substitute x + y = z after seperating dx and dy]
Ans.
Given differential equation is (x + y) (dx – dy) = dx + dy
⇒ (x + y) dx – (x + y) dy = dx + dy
⇒ – (x + y) dy – dy = dx – (x + y) dx
⇒ – (x + y + 1) dy = – (x + y – 1) dx
⇒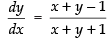
Put x + y = z
∴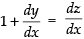
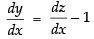
So,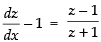
⇒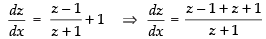
⇒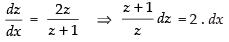
Integrating both sides, we get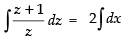
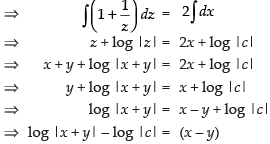
⇒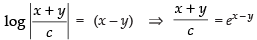
∴ x + y = c . ex – y
Hence, the required solution is x + y = c . ex – y.
Q.20. Solve: 2(y + 3) – xy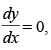 given that y (1) = – 2.
given that y (1) = – 2.
Ans.
Given differential equation is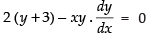
⇒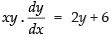
⇒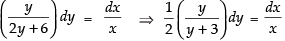
Integrating both sides, we get
⇒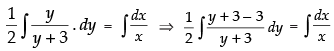
⇒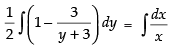
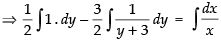
⇒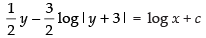
Put x = 1, y = –2
⇒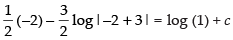
⇒
⇒ – 1 – 0 = 0 + c [∵ log (1) = 0]
∴ c = –1
∴ equation is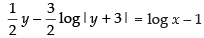
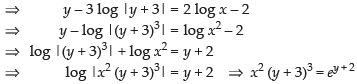
Hence, the required solution is x2 (y + 3)3 = ey + 2
Q.21. Solve the differential equation dy = cos x (2 – y cosec x) dx given that y = 2 when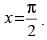
Ans.
The given differential equation is
dy = cos x (2 – y cosec x) dx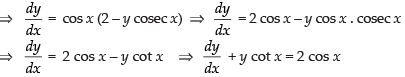
Here, P = cot x and Q = 2 cos x.
∴ Integrating factor I.F. =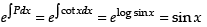
∴ Required solution is y × I.F =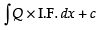
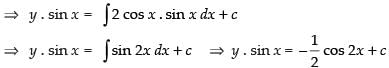
Put x =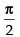 and y = 2, we get
and y = 2, we get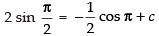
⇒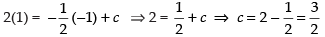
∴ The equation is y sin x =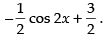
Q.22. Form the differential equation by eliminating A and B in Ax2 + By2 = 1.
Ans.
Given that Ax2 + By2 = 1
Differentiating w.r.t. x, we get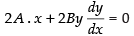
⇒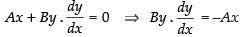
∴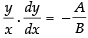
Differentiating both sides again w.r.t. x, we have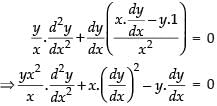
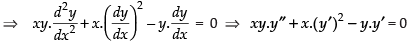
Hence, the required equation is
xy.y ″ + x.( y ′)2- y.y′ = 0
Q.23. Solve the differential equation (1 + y2) tan–1x dx + 2y (1 + x2) dy = 0.
Ans.
Given differential equation is
(1 + y2) tan–1x dx + 2y (1 + x2) dy = 0
⇒ 2y (1 + x2) dy = –(1 + y2) . tan–1x . dx
⇒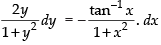
Integrating both sides, we get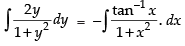
⇒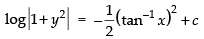
⇒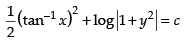
Which is the required solution.
Q.24. Find the differential equation of system of concentric circles with centre (1, 2).
Ans.
Family of concentric circles with centre (1, 2) and radius ‘r’ is
(x – 1)2 + (y – 2)2 = r2
Differentiating both sides w.r.t., x we get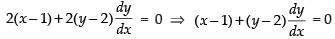
Which is the required equation.
LONG ANSWER TYPE QUESTIONS
Q.25. Solve :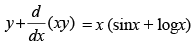
Ans.
The given differential equation is
⇒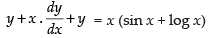
⇒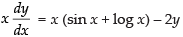
⇒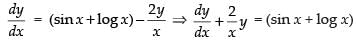
Here, P =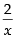 and Q = (sin x + log x)
and Q = (sin x + log x)
Integrating factor I.F. =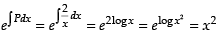
∴ Solution is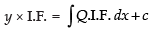
⇒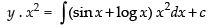 ...(1)
...(1)
Let I
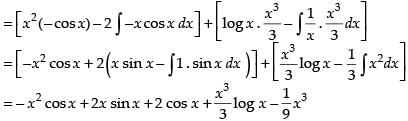
Now from eq (1) we get,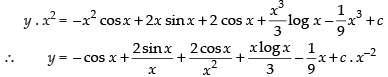
Hence, the required solution is
Q.26. Find the general solution of (1 + tany) (dx – dy) + 2xdy = 0.
Ans.
Given that: (1 + tan y) (dx – dy) + 2xdy = 0
⇒ (1 + tan y) dx – (1 + tan y) dy + 2xdy = 0
⇒ (1 + tan y) dx – (1 + tan y – 2x) dy = 0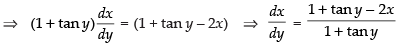
⇒
Here, P =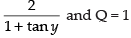
Integrating factor I.F.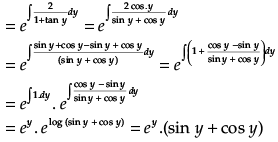
So, the solution is x × I.F. =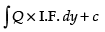
⇒ x . ey (sin y + cos y) =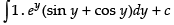
⇒ x . ey (sin y + cos y) = ey . sin y + c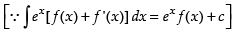
⇒ x(sin y + cos y) = sin y + c . e–y
Hence, the required solution is x(sin y + cos y) = sin y + c . e–y.
Q.27. Solve :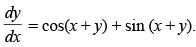 [Hint: Substitute x + y = z]
[Hint: Substitute x + y = z]
Ans.
Given that :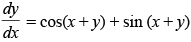
Put x + y = v, on differentiating w.r.t. x, we get,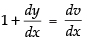
∴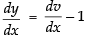
∴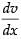 -1 = cos v + sin v
-1 = cos v + sin v
⇒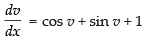
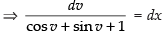
Integrating both sides, we have
⇒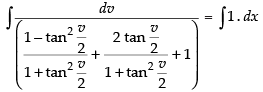
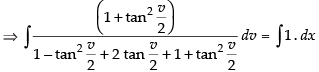
⇒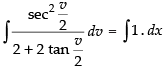
Put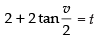
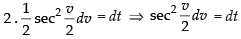
⇒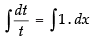
⇒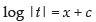
⇒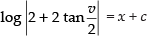
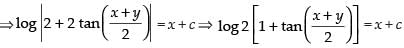
⇒
⇒
Hence, the required solution is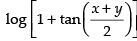 = x + K [c – log 2 = K]
= x + K [c – log 2 = K]
Q.28. Find the general solution of 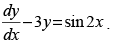
Ans.
Given equation is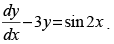
Here, P = –3 and Q = sin 2 x
∴ Integrating factor I.F. =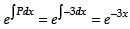
∴ Solution is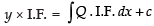
⇒
Let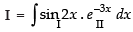
⇒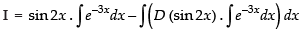
⇒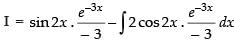
⇒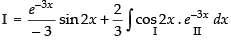
⇒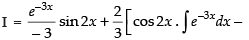
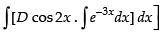
⇒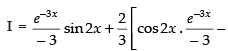
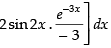
⇒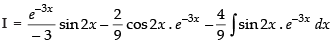
⇒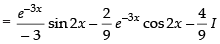
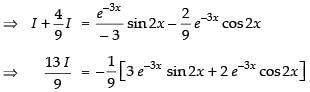
⇒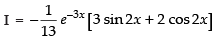
∴ The equation becomes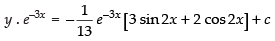
∴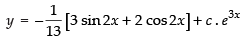
Hence, the required solution is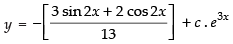
Q.29. Find the equation of a curve passing through (2, 1) if the slope of the tangent to the curve at any point (x, y) is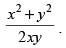
Ans.
Given that the slope of tangent to a curve at (x, y) is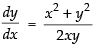
It is a homogeneous differential equation
So, put y = vx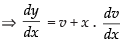
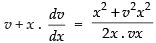

⇒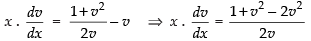
⇒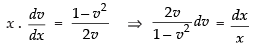
Integrating both sides, we get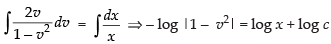
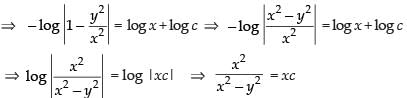
Since, the curve is passing through the point (2, 1)
∴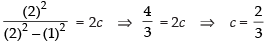
Hence, the required equation is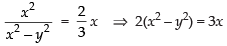
Q.30. Find the equation of the curve through the point (1, 0) if the slope of the tangent to the curve at any point (x, y) is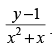
Ans.
Given that the slope of the tangent to the curve at (x, y) is
Integrating both sides, we have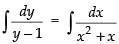
⇒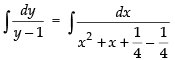 [making perfect square]
[making perfect square]
⇒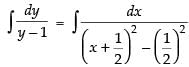
⇒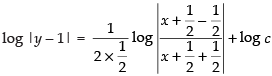
⇒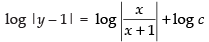
⇒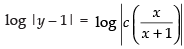
∴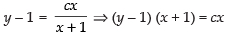
Since, the line is passing through the point (1, 0), then
(0 – 1) (1 + 1) = c(1) ⇒ c = 2.
Hence, the required solution is (y – 1) (x + 1) = 2x.
Q.31. Find the equation of a curve passing through origin if the slope of the tangent to the curve at any point (x, y) is equal to the square of the difference of the abcissa and ordinate of the point.
Ans.
Here, slope of the tangent of the curve =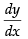
and the difference between the abscissa and ordinate = x – y.
∴ As per the condition,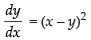
Put x – y = v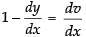
∴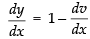
∴ the equation becomes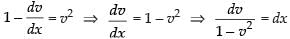
Integrating both sides, we get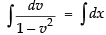
⇒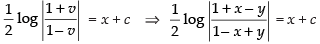 ...(1)
...(1)
Since, the curve is passing through (0, 0)
then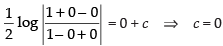
∴ On putting c = 0 in eq. (1) we get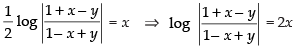
∴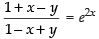
⇒ (1 + x – y) = e2x (1 – x + y)
Hence, the required equation is (1 + x – y) = e2x (1 – x + y).
Q.32. Find the equation of a curve passing through the point (1, 1). If the tangent drawn at any point P (x, y) on the curve meets the co-ordinate axes at A and B such that P is the mid-point of AB.
Ans.
Let P (x, y) be any point on the curve and AB be the tangent to the given curve at P.
P is the mid point of AB (given)
∴ Coordinates of A and B are (2x, 0) and (0, 2y) respectively.
∴ Slope of the tangent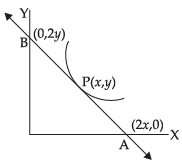
AB =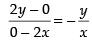
∴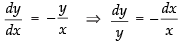
Integrating both sides, we get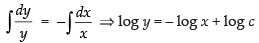
⇒ log y + log x = log c ⇒ log yx = log c
∴ yx = c
Since, the curve passes through (1, 1)
∴ 1 × 1 = c ∴ c = 1
⇒ yx = 1
Hence, the required equation is xy = 1.
Q.33. Solve :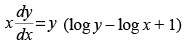
Ans.
Given that: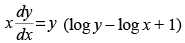
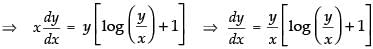
Since, it is a homogeneous differential equation.
∴ Put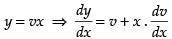
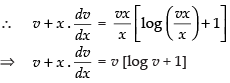
⇒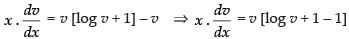
⇒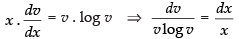
Integrating both sides, we get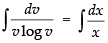
Put log v = t on L.H.S.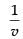 dv = dt
dv = dt
∴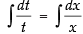
log|t| = log|x| + log c
⇒ log |log v| = log xc ⇒ log v = xc
⇒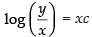
Hence, the required solution is log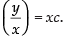
OBJECTIVE TYPE QUESTIONS
Q.34. The degree of the differential equation
(a) 1
(b) 2
(c) 3
(d) not defined
Ans. (d)
Solution.
The degree of the given differential equation is not defined
because the value of sin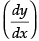 on expansion will be in increasing power of
on expansion will be in increasing power of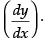
Hence, the correct option is (d).
Q.35. The degree of the differential equation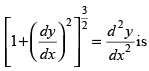
(a) 4
(b) 3/2
(c) not defined
(d) 2
Ans. (d)
Solution.
The given differential equation is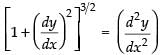
Squaring both sides, we have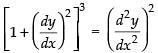
So, the degree of the given differential equation is 2.
Hence, the correct option is (d).
Q.36. T he order and degree of the differential equation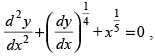 respectively are
respectively are
(a) 2 and not defined
(b) 2 and 2
(c) 2 and 3
(d) 3 and 3
Ans. (a)
Solution.
Given differential equation is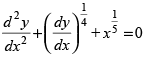
⇒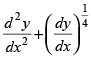
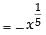
Since the degree of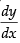 is in fraction.
is in fraction.
So, the degree of the differential equation is not defined as the order is 2.
Hence, the correct option is (a).
Q.37. If y = e–x (Acosx + Bsinx), then y is a solution of
(a)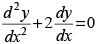
(b)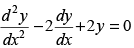
(c)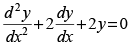
(d)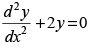
Ans. (c)
Solution.
Given equation is y = e–x (A cos x + B sin x)
Differentiating both sides, w.r.t. x, we get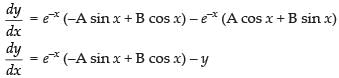
Again differentiating w.r.t. x, we get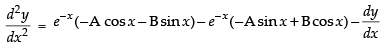
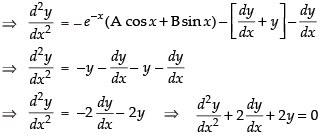
Hence, the correct option is (c)
Q.38. The differential equation for y = Acos αx + Bsin αx, where A and B are arbitrary constants is
(a)
(b)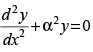
(c)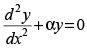
(d)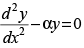
Ans. (b)
Solution.
Given equation is : y = A cos α x + B sin α x
Differentiating both sides w.r.t. x, we have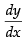 = –A sin α x . α + B cos α x . α
= –A sin α x . α + B cos α x . α
= –A α sin α x + B α cos α x
Again differentiating w.r.t. x, we get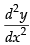 = –A α2 cos α x – B α2 sin α x
= –A α2 cos α x – B α2 sin α x
⇒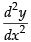 = – α2 (A cos α x + B sin α x)
= – α2 (A cos α x + B sin α x)
⇒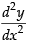 = – α2 y ⇒
= – α2 y ⇒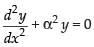
Hence, the correct option is (b).
Q.39. Solution of differential equation xdy – ydx = 0 represents :
(a) a rectangular hyperbola
(b) parabola whose vertex is at origin
(c) straight line passing through origin
(d) a circle whose centre is at origin.
Ans. (c)
Solution.
The given differential equation is
xdy – ydx = 0
⇒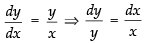
Integrating both sides, we get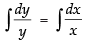
⇒ log y = log x + log c ⇒ log y = log xc
⇒ y = xc which is a straight line passing through the origin.
Hence, the correct answer is (c).
Q.40. Integrating factor of the differential equation cosx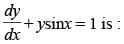
(a) cos x
(b) tan x
(c) sec x
(d) sin x
Ans. (c)
Solution.
The given differential equation is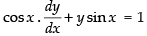
⇒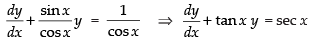
Here, P = tan x and Q = sec x
∴ Integrating factor =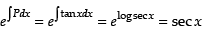
Hence, the correct option is (c).
Q.41. Solution of the differential equation tany sec2x dx + tanx sec2ydy = 0 is :
(a) tan x + tan y = k
(b) tan x – tan y = k
(c)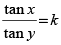
(d) tanx . tany = k
Ans. (d)
Solution.
The given differential equation is
tan y sec2 x dx + tan x sec2 y dy = 0
⇒ tan x sec2 y dy = - tan y sec2 x dx
⇒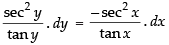
Integrating both sides, we get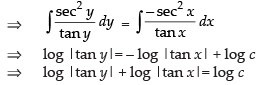
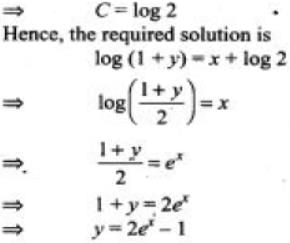
Q.42. Family y = Ax + A3 of curves is represented by the differential
equation of degree
(a) 1
(b) 2
(c) 3
(d) 4
Ans. (a)
Solution.
Given equation is y = Ax + A3
Differentiating both sides, we get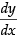 = A which has degree 1.
= A which has degree 1.
Hence, the correct answer is (a).
Q.43. Integrating factor of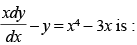
(a) x
(b) log x
(c) 1/x
(d) – x
Ans. (c)
Solution.
The given differential equation is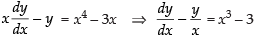 ⇒
⇒
Here,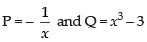
So, integrating factor =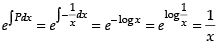
Hence, the correct option is (c).
Q.44. Solution of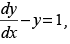 y (0) = 1 is given by
y (0) = 1 is given by
(a) xy = – ex
(b) xy = – e–x
(c) xy = – 1
(d) y = 2 ex – 1
Ans. (d)
Solution.
The given differential equation is
Here, P = –1, Q = 1
∴ Integrating factor, I.F. =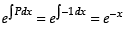
So, the solution is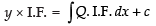
⇒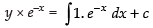
⇒ y . e–x = – e–x + c
Put x = 0, y = 1
⇒ 1 . e0 = – e0 + c
⇒ 1 = –1 + c ∴ c = 2
So the equation is y . e–x = –e–x + 2
⇒ y = – 1 + 2ex = 2ex – 1
Hence, the correct option is (d).
Q.45. The number of solutions of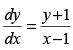 when y (1) = 2 is
when y (1) = 2 is
(a) none
(b) one
(c) two
(d) infinite
Ans. (b)
Solution.
The given differential equation is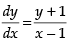
⇒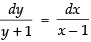
Integrating both sides, we get
⇒ log (y + 1) = log (x – 1) + log c
⇒ log (y + 1) – log (x – 1) = log c
⇒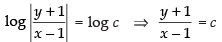
Put x = 1 and y = 2
⇒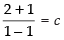 ∴ c = ∞
∴ c = ∞
∴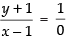 ⇒ x – 1 = 0 ⇒ x = 1
⇒ x – 1 = 0 ⇒ x = 1
Hence, the correct option is (b).
Q.46. Which of the following is a second order differential equation?
(a) (y′)2 + x = y2
(b) y′y′′+ y = sin x
(c) y″ + (y'')2 + y = 0
(d) y′ = y2
Ans. (b)
Solution.
Second order differential equation is y′y″+ y = sin x
Hence, the correct option is (b).
Q.47. Integrating factor of the differential equation (1 – x2)
(a) –x
(b)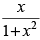
(c)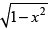
(d)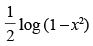
Ans. (c)
Solution.
The given differential equation is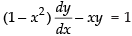
⇒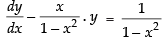
Here,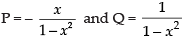
∴ Integrating factor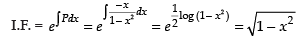
Hence, the correct option is (c).
Q.48. tan–1 x + tan–1 y = c is the general solution of the differential equation:
(a)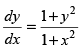
(b)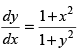
(c) (1 + x2) dy + (1 + y2) dx = 0
(d) (1 + x2) dx + (1 + y2) dy = 0
Ans. (c)
Solution.
Given equation is tan–1x + tan–1y = c
Differentiating w.r.t. x, we have
⇒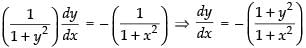
⇒(1 + x2) dy = – (1 + y2) dx
⇒ (1 + x2) dy + (1 + y2) dx = 0
Hence the correct option is (c).
Q.49. The differential equation y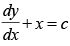 represents :
represents :
(a) Family of hyperbolas
(b) Family of parabolas
(c) Family of ellipses
(d) Family of circles
Ans. (d)
Solution.
Given differential equation is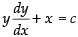
⇒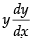 = c – x ⇒ y dy = (c – x) dx
= c – x ⇒ y dy = (c – x) dx
∴ Integrating both sides, we get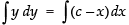
⇒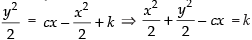
⇒ x2 + y2 – 2cx = 2k which is a family of circles.
Hence, the correct option is (d).
Q.50. The general solution of ex cosy dx – ex siny dy = 0 is :
(a) ex cos y = k
(b) ex sin y = k
(c) ex = k cos y
(d) ex = k sin y
Ans. (a)
Solution.
The given differential equation is
ex cos y dx – ex sin y dy = 0
⇒ ex (cos y dx – sin y dy) = 0
⇒ cos y dx - sin y dy = 0 [∵ ex ≠ 0]
⇒ sin y dy = cos y dx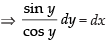
Integrating both sides, we have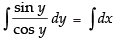
⇒ - log |cos y| = x + log k ⇒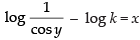
⇒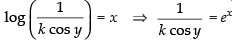
⇒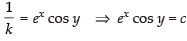
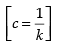
Hence, the correct option is (a).
Q.51. The degree of the differential equation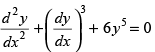 is
is
(a) 1
(b) 2
(c) 3
(d) 5
Ans. (a)
Solution.
The degree of the given differential equation is 1 as the power of the highest order is 1.
Hence, the correct option is (a).
Q.52. The solution of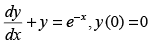 is
is
(a) y = ex (x – 1)
(b) y = xe–x
(c) y = x e–x + 1
(d) y = (x + 1) e–x
Ans. (b)
Solution.
The given differential equation is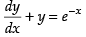
Since, it is a linear differential equation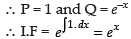
So, the solution is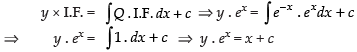
Put x = 0, y = 0, we have 0 = 0 + c ∴ c = 0
So, the solution is y ex = x ⇒ y = x . e–x
Hence, the correct option is (b).
Q.53. Integrating factor of the differential equation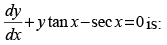
(a) cos x
(b) sec x
(c) ecos x
(d) esec x
Ans. (b)
Solution.
Given differential equation is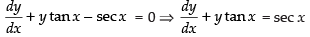
Here, P = tan x and Q = sec x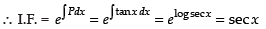
Hence, the correct option is (b).
Q.54. The solution of the differential equation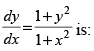
(a) y = tan–1 x
(b) y – x = k (1 + xy)
(c) x = tan–1 y
(d) tan (xy) = k
Ans. (b)
Solution.
The given differential equation is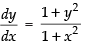 ⇒
⇒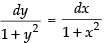
Integrating both sides, we get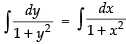
⇒tan–1 y = tan–1 x + c ⇒ tan-1 y - tan-1 x = c
⇒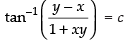
⇒
⇒ y – x = k (1 + xy)
Hence, the correct option is (b).
Q.55. The integrating factor of the differential equation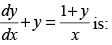
(a)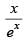
(b)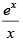
(c) xex
(d) ex
Ans. (b)
Solution.
The given differential equation is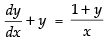
⇒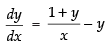
⇒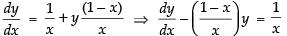
Here, P =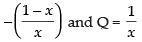
∴ Integrating factor I.F.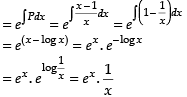
Hence, the correct option is (b).
Q.56. y = aemx + be–mx satisfies which of the following differential equation?
(a)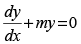
(b)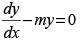
(c)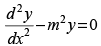
(d)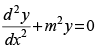
Ans. (c)
Solution.
The given equation is y = aemx + be–mx
On differentiation, we get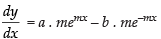
Again differentiating w.r.t., we have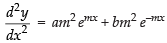
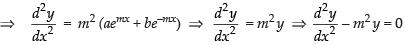
Hence, the correct option is (c).
Q.57. The solution of the differential equation cosx siny dx + sinx cosy dy = 0
is :
(a)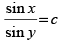
(b) sin x sin y = c
(c) sin x + sin y = c
(d) cos x cos y = c
Ans. (b)
Solution.
The given differential equation is
cos x sin y dx + sin x cos y dy = 0
⇒ sin x cos y d y = – cos x sin y dx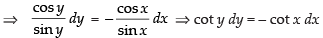
Integrating both sides, we have
⇒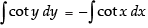
⇒ log |sin y| = – log |sin x| + log c
⇒ log |sin y| + log |sin x| = log c
⇒ log |sin y . sin x| = log c ⇒ sin x sin y = c
Hence, the correct option is (b).
Q.58. The solution of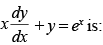
(a)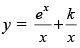
(b) y = xex + cx
(c) y = x . ex + k
(d)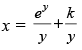
Ans. (a)
Solution.
The given differential equation is
⇒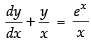
Here P 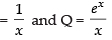
∴ Integrating factor I.F. =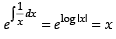
So, the solution is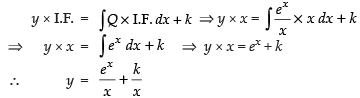
Hence, the correct option is (a).
Q.59. The differential equation of the family of curves x2 + y2 – 2ay = 0, where a is arbitrary constant, is:
(a)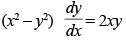
(b)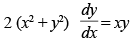
(c)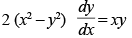
(d)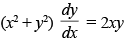
Ans. (a)
Solution.
The given equation is
x2 + y2 – 2ay = 0 ..(1)
Differentiating w.r.t. x, we have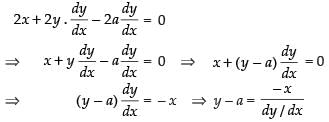
⇒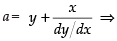
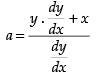
Putting the value of a in eq. (1) we get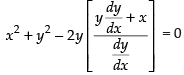
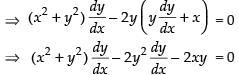
⇒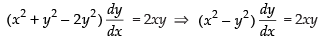
∴ Hence the correct option is (a).
Q.60. Family y = Ax + A3 of curves will correspond to a differential equation of order
(a) 3
(b) 2
(c) 1
(d) not defined
Ans. (b)
Solution.
The given equation is
y = Ax + A3
Differentiating both sides, we get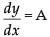
Again differentiating both sides, we have
So the order of the differential equation is 2.
Hence, the correct option is (b).
Q.61. The general solution of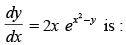
(a)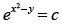
(b)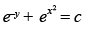
(c)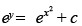
(d)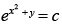
Ans. (c)
Solution.
The given differential equation is
⇒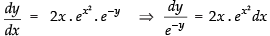
Integrating both sides, we have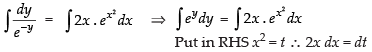
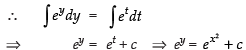
Hence, the correct option is (c).
Q.62. The curve for which the slope of the tangent at any point is equal to the ratio of the abcissa to the ordinate of the point is
(a) an ellipse
(b) parabola
(c) circle
(d) rectangular hyperbola
Ans. (d)
Solution.
Since, the slope of the tangent to the curve = x : y
∴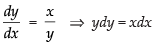
Integrating both sides, we get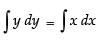
⇒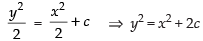
⇒ y2 – x2 = 2c = k which is rectangular hyperbola.
Hence, the correct option is (d).
Q.63. The general solution of the differential equation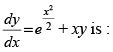
(a)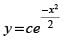
(b)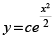
(c)
(d)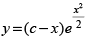
Ans. (c)
Solution.
The given differential equation is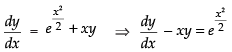
Since it is linear differential equation where P = –x and Q =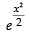
∴ Integrating factor I.F. =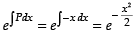
So, the solution is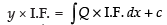
⇒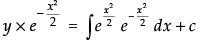
⇒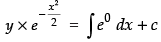
⇒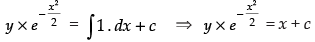
∴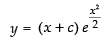
Hence the correct option is (c).
Q.64. The solution of the equation (2y – 1) dx – (2x + 3)dy = 0 is :
(a)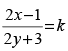
(b)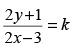
(c)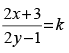
(d)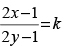
Ans. (c)
Solution.
The given differential equation is
(2y – 1) dx – (2x + 3) dy = 0 ⇒ (2x + 3) dy = (2y - 1) dx
⇒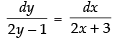
Integrating both sides, we get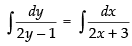
⇒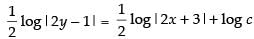
⇒log |2y – 1| = log |2x + 3| + 2 log c
⇒ log |2y – 1| – log |2x + 3| = log c2
⇒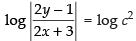
⇒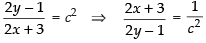
⇒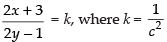
Hence, the correct option is (c).
Q.65. The differential equation for which y = acosx + bsinx is a solution, is :
(a)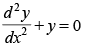
(b)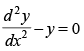
(c)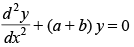
(d)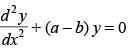
Ans. (a)
Solution.
The given equation is
y = a cos x + b sin x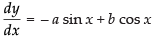
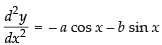
⇒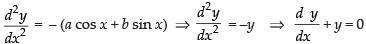
Hence, the correct option is (a).
Q.66. The solution of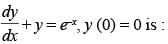
(a) y = e–x (x – 1)
(b) y = x . ex
(c) y = x e–x + 1
(d) y = x . e–x
Ans. (d)
Solution.
The given differential equation is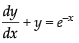
Since, it is a linear differential equation then P = 1 and Q = e–x
Integrating factor I.F. =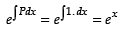
∴ Solution is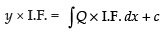
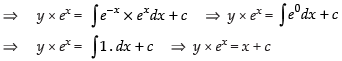
Put y = 0 and x = 0
∴ 0 = 0 + c ∴ c = 0
∴ equation is y × ex = x
So y = x . e–x
Hence, the correct option is (d).
Q.67. The order and degree of the differential equation
(a) 1, 4
(b) 3, 4
(c) 2, 4
(d) 3, 2
Ans. (d)
Solution.
The given differential equation is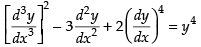
Here the highest derivative is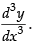
∴ the order of the differential equation is 3
and since, the power of highest order is 2
∴ its degree is 2
Hence, the correct option is (d).
Q.68. The order and degree of the differential equation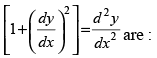
(a)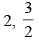
(b) 2, 3
(c) 2, 1
(d) 3, 4
Ans. (c)
Solution.
The given differential equation is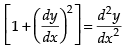
Here, the highest derivative is 2,
∴ order = 2
and the power of the highest derivative is 1
∴ degree = 1
Hence, the correct option is (c).
Q.69. The differential equation of the family of curves y2 = 4a (x + a) is :
(a)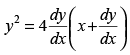
(b)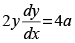
(c)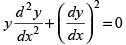
(d)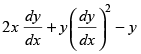
Ans. (d)
Solution.
The given equation of family of curves is
y2 = 4a (x + a)
⇒ y2 = 4ax + 4a2 ...(1)
Differentiating both sides, w.r.t. x, we get
⇒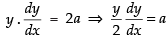
Now, putting the value of a in eq. (1) we get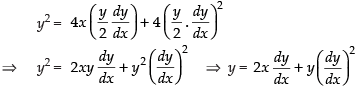
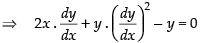
Hence, the correct option is (d).
Q.70. Which of the following is the general solution of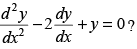
(a) y = (Ax + B) . ex
(b) y = (Ax + B) e–x
(c) y = Aex + Be–x
(d) y = A cos x + B sin x
Ans. (a)
Solution.
The given differential equation is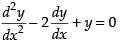
Since the above equation is of second order and first degree
∴ D2y – 2Dy + y = 0, where D =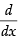
⇒ (D2 - 2D + 1) y = 0
∴ auxiliary equation is
m2 - 2m + 1 = 0 ⇒ (m - 1)2 = 0 ⇒ m = 1, 1
If the roots of Auxiliary equation are real and equal say (m)
then CF = (c1 x + c2) . emx
∴ CF = (Ax + B) ex
So y = (Ax + B) . ex
Hence, the correct option is (a).
Q.71. General solution of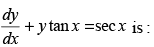
(a) y sec x = tan x + c
(b) y tan x = sec x + c
(c) tan x = y tan x + c
(d) x sec x = tan y + c
Ans. (a)
Solution.
The given differential equation is
Since, it is a linear differential equation
∴ P = tan x and Q = sec x
Integrating factor I.F. =
∴ Solution is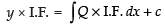
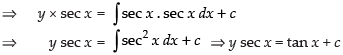
Hence, the correct option is (a).
Q.72. Solution of the differential equation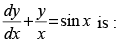
(a) x (y + cos x) = sin x + c
(b) x (y – cos x) = sin x + c
(c) xy cos x = sin x + c
(d) x (y + cos x) = cos x + c
Ans. (a)
Solution.
The given differential equation is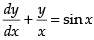
Since, it is a linear differential equation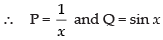
Integrating factor I.F. =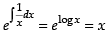
∴ Solution is y × I.F. =
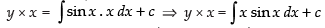
⇒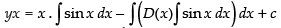
⇒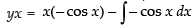
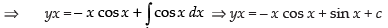
⇒ yx + x cos x = sin x + c
⇒ x (y + cos x) = sin x + c
Hence, the correct option is (a).
Q.73. The general solution of the differential equation (ex + 1) ydy = (y + 1) exdx is:
(a) (y + 1) = k (ex + 1)
(b) y + 1 = ex + 1 + k
(c) y = log [k (y + 1) (ex + 1)]
(d)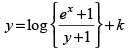
Ans. (c)
Solution.
The given differential equation is
(ex + 1) y dy = (y + 1) ex dx
⇒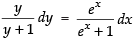
Integrating both sides, we get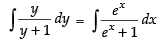
⇒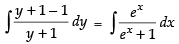
⇒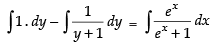
⇒ y – log |y + 1| = log |ex + 1| + log k
⇒ y = log |y + 1| + log |ex + 1| + log k
⇒ y = log |k (y + 1) (ex + 1)|
Hence, the correct option is (c).
Q.74. The solution of the differential equation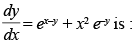
(a) y = e x -y- x2 e- y + c
(b)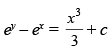
(c)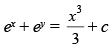
(d)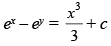
Ans. (b)
Solution.
The given differential equation is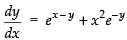
⇒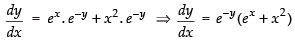
⇒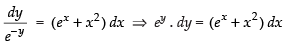
Integrating both sides, we have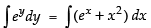
⇒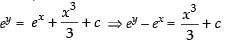
Hence, the correct option is (b).
Q.75. The solution of the differential equation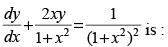
(a) y (1 + x2) = c + tan–1 x
(b)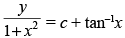
(c) y log (1 + x2) = c + tan–1 x
(d) y (1 + x2) = c + sin–1 x
Ans. (a)
Solution.
The given differential equation is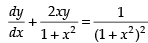
Since, it is a linear differential equation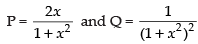
Integrating factor I.F. =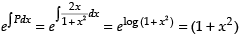
∴ Solution is y × I.F. =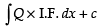
⇒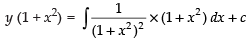
⇒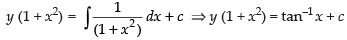
Hence, the correct option is (a).
Q.76. Fill in the blanks
(i) The degree of the differential equation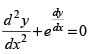 is _________.
is _________.
(ii) The degree of the differential equation is _________.
is _________.
(iii) The number of arbitrary constants in the general solution of a differential equation of order three is _________.
(iv)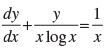 is an equation of the type _________.
is an equation of the type _________.
(v) General solution of the differential equation of the type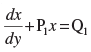
is given by _________.
(vi) The solution of the differential equation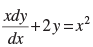 is _________.
is _________.
(vii) The solution of (1 + x2)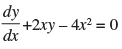 is _________.
is _________.
(viii) The solution of the differential equation ydx + (x + xy)dy = 0 is ______.
(ix) General solution of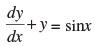 is _________.
is _________.
(x) The solution of differential equation coty dx = xdy is _________.
(xi) The integrating factor of is _________.
is _________.
Ans.
(i) The degree of the differential equation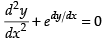 is not defined.
is not defined.
(ii) The given differential equation is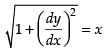
Squaring both sides, we get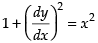
So, the degree of the equation is 2.
(iii) The number of arbitrary constants in the solution is 3.
(iv) The given differential equation is of the
is of the
type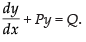
(v) General solution of the differential equation of the type
(vi) The given differential equation is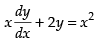
⇒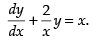
Since, it is linear differential equation
∴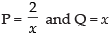
Integrating factor I.F. =
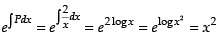
∴ Solution is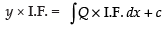
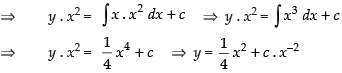
Hence, the solution is y =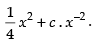
(vii) The given differential equation is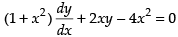
⇒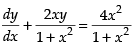
Since it is a linear differential equation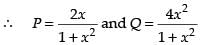
Integrating factor I.F. =

∴ Solution is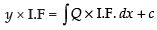
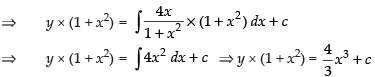
⇒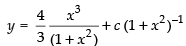
Hence, the required solution is y =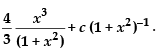
(viii) The given differential equation is
ydx + (x + xy) dy = 0
⇒ (x + xy) dy = – y dx ⇒ x (1 + y) dy = – y dx
⇒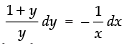
Integrating both sides, we get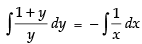
⇒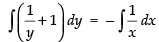
⇒ log y + y = – log x + log c
⇒ log x + log y + log ey = log c
⇒ log (xy . ey) = log c
∴ xy = c e–y
Hence, the required solution is xy = c e–y.
(ix) The given differential equation is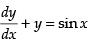
Since, it a linear differential equation
∴ P = 1 and Q = sin x
Integrating factor I.F. =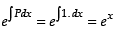
∴ Solution is y × I.F. =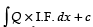
⇒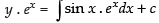 ...(1)
...(1)
Let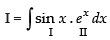
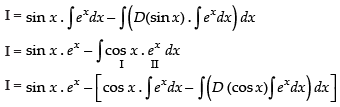
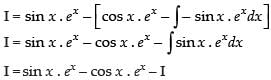
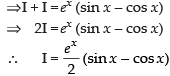
From eq. (1) we get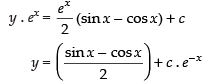
Hence, the required solution is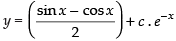
(x) The given differential equation is cot y dx = x dy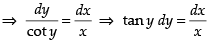
Integrating both sides, we get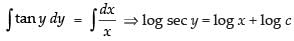
⇒ log sec y – log x = log c
⇒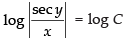
∴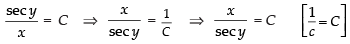
∴ x = C sec y
Hence, the required solution is x = C sec y .
(xi) The given differential equation is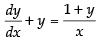
⇒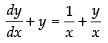
⇒
Here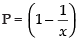
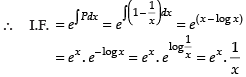
Hence, the required I.F. =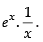
Q.77. State True or False for the following:
(i) Integrating factor of the differential of the form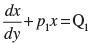
is given by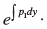
(ii) Solution of the differential equation of the type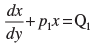
is given by x.I.F. =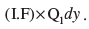
(iii) Correct substitution for the solution of the differential equation
of the type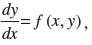 where f (x, y) is a homogeneous function of zero
where f (x, y) is a homogeneous function of zero
degree is y = vx.
(iv) Correct substitution for the solution of the differential equation
of the type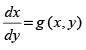 where g (x, y) is a homogeneous function of the degree zero is x = vy.
where g (x, y) is a homogeneous function of the degree zero is x = vy.
(v) Number of arbitrary constants in the particular solution of a differential equation of order two is two.
(vi) The differential equation representing the family of circles x2 + (y – a)2 = a2 will be of order two.
(vii) The solution of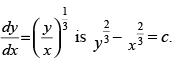
(viii) Differential equation representing the family of curves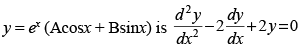
(ix) The solution of the differential equation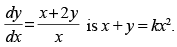
(x) Solution of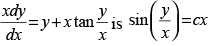
(xi) The differential equation of all non horizontal lines in a plane is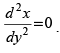
Ans.
(i) True
I.F. of the given differential equation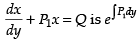
(ii) True
(iii) True
(iv) True
(v) False
Since particular solution of a differential equation has no arbitrary constant.
(vi) False
We know that the order of the differential equation is equal to the number of arbitrary constants.
(vii) True The given differential equation is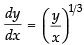
⇒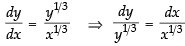
Integrating both sides, we get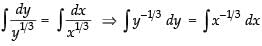
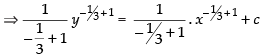
⇒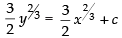
⇒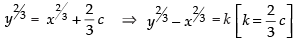
(viii) True
Given equation is y = ex (A cos x + B sin x)
Differentiating both sides, we get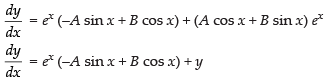
Again differentiating w.r.t. x, we get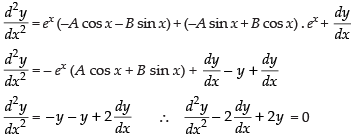
(ix) True
The given differential equation is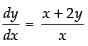
⇒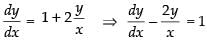
Here,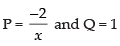
Integrating factor I.F. =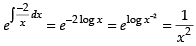
∴ Solution is y × I.F. =
⇒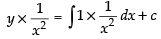
⇒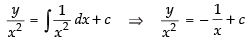
⇒ y = – x + cx2 ⇒ y + x = cx2
(x) True The given differential equation is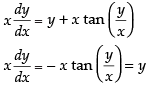
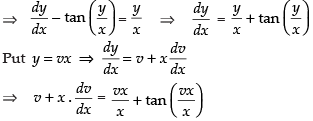

Integrating both sides, we get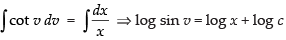
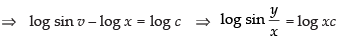
∴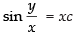
(xi) True
Let y = mx + c be the non-horizontal line in a plane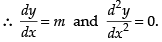
|
172 videos|487 docs|154 tests
|
FAQs on NCERT Exemplar: Differential Equations - Mathematics (Maths) for JEE Main & Advanced
| 1. What are differential equations? |  |
| 2. How are differential equations classified? |  |
| 3. What is the order of a differential equation? |  |
| 4. How can differential equations be solved? |  |
| 5. What are the applications of differential equations? |  |
















