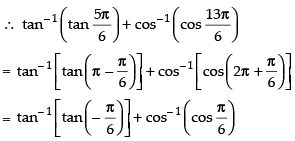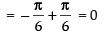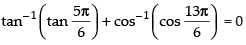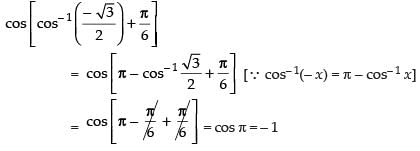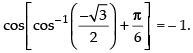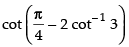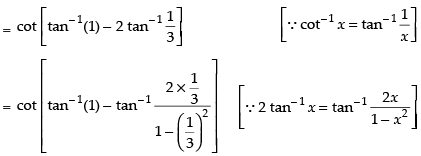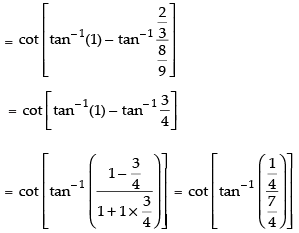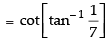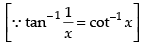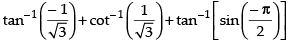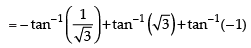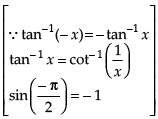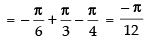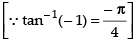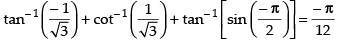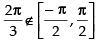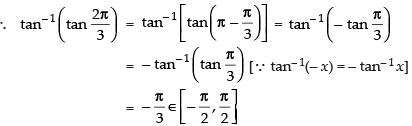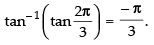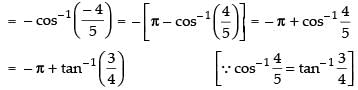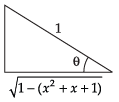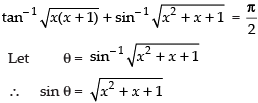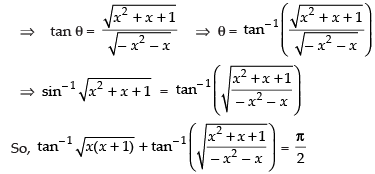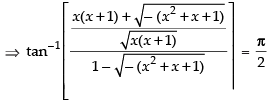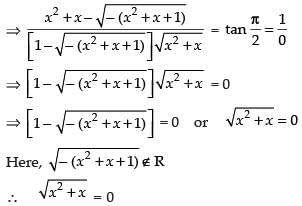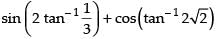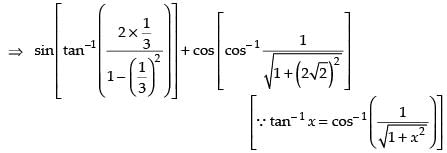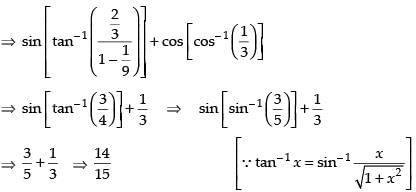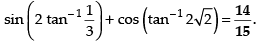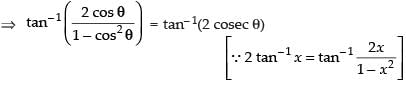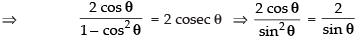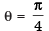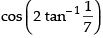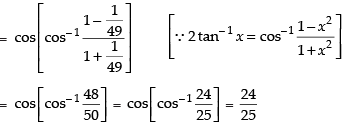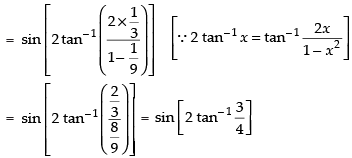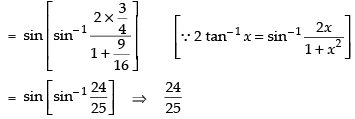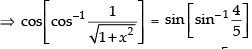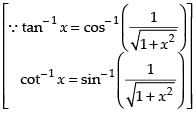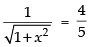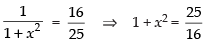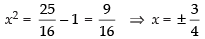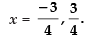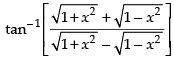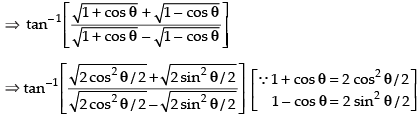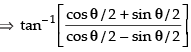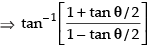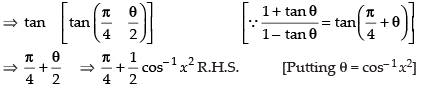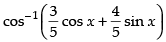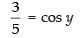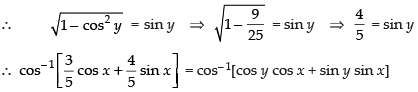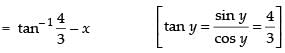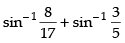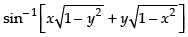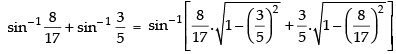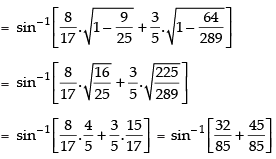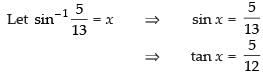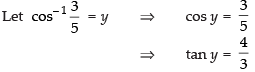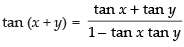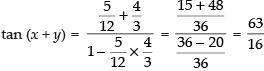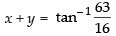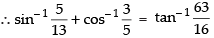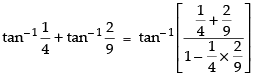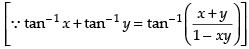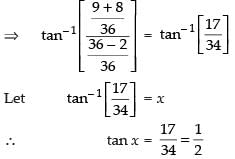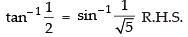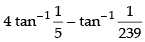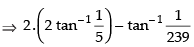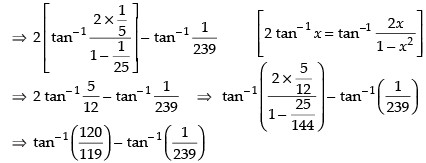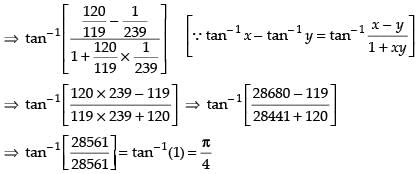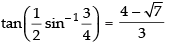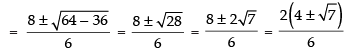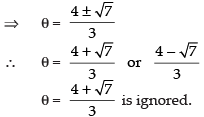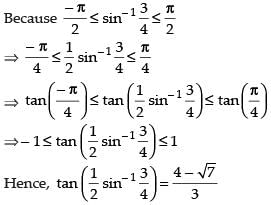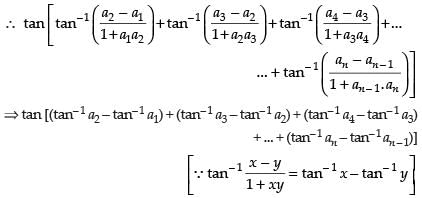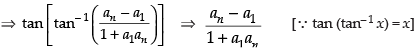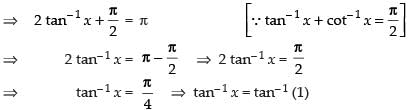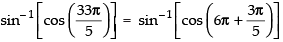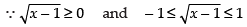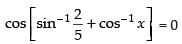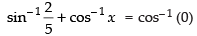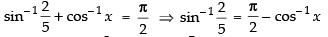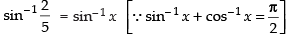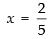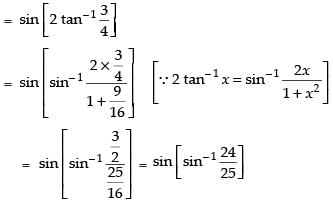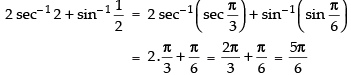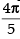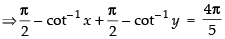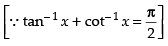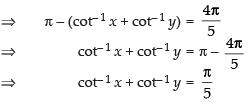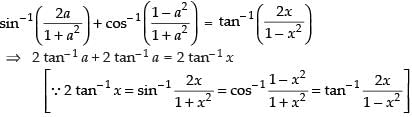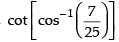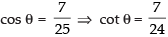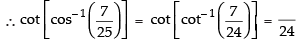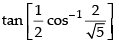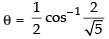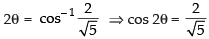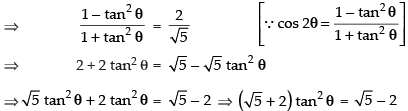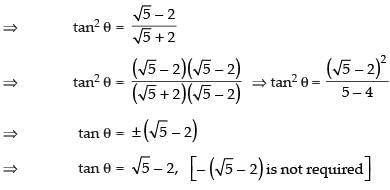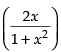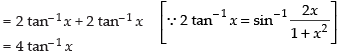NCERT Exemplar: Inverse Trigonometric Functions | Mathematics (Maths) for JEE Main & Advanced PDF Download
| Table of contents |

|
| Short Answer Type Questions |

|
| Long Answer Type Questions |

|
| Objective Type Questions |

|
| Fill in the blanks |

|
| State True or False |

|
Short Answer Type Questions
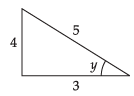
Que 1: Find the value of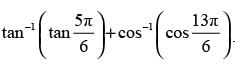
Ans:
We know that[∵ tan- 1(- x) = - tan - 1 x]
Hence,
Que 2: Evaluate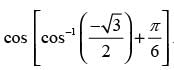
Ans.
Hence,
Que 3: Prove that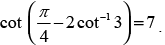
Ans:
L.H.S.
= cot [cot– 1 (7)] = 7 R.H.S.
Hence proved.
Que 4: Find the value of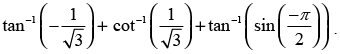
Ans:
Hence,
Que 5: Find the value of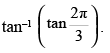
Ans:
We know that
Hence,
Que 6: Show that 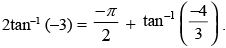
Ans:
L.H.S. 2 tan– 1 (– 3) = – 2 tan– 1 (3)
Hence proved.
Que 7: Find the real solutions of the equation
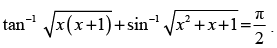
Ans:////
⇒ x2 + x = 0 ⇒ x(x + 1) = 0
⇒ x = 0 or x + 1 = 0 ⇒ x = 0 or x = – 1
Hence the real solutions are x = 0 and x = – 1.
Alternate Method:
⇒ x2 + x + 1 = 1 ⇒ x2 + x = 0
⇒ x(x + 1) = 0 ⇒ x = 0 or x + 1 = 0
∴ x = 0, x = – 1
Que 8: Find the value of the expression
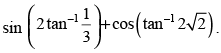
Ans:
Hence,
Que 9: If 2 tan–1 (cos θ) = tan–1 (2 cosec θ), then show that θ =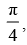
where n is any integer.
Ans:
2 tan– 1(cos θ) = tan– 1(2 cosec θ)
⇒ cos θ sin θ = sin2θ
⇒ cos θ sin θ – sin2θ = 0 ⇒ sin θ(cos θ - sin θ) = 0
⇒ sin θ = 0 or cos θ - sin θ = 0 ⇒ sin θ = 0 or 1 - tan θ = 0
⇒ θ = 0 or tan θ = 1 ⇒ θ = 0° or
Hence proved.
Que 10: Show that 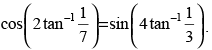
Ans.
L.H.S.
R.H.S.
L.H.S. = R.H.S. Hence proved.
Que 11: Solve the following equation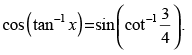
Ans.
Given that
⇒
Squaring both sides we get,
⇒
Hence,
Long Answer Type Questions
Que 12: Prove that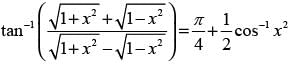
Ans:
L.H.S.
Put x2 = cos θ ∴ θ = cos– 1 x2
[Dividing the Nr. and Den. by cos θ/2]
Hence proved.
Que 13: Find the simplified form of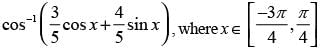
Ans:
Given that
Put
= cos– 1 [cos (y – x)] = y – x
Que 14: Prove that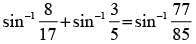
Ans:
L.H.S
Using sin– 1 x + sin– 1 y =R.H.S. Hence proved.
Que 15: Show that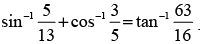
Ans:
Now
⇒
⇒
Hence proved.
Que 16: Prove that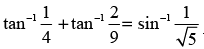
Ans:
∴
Hence,
Que 17: Find the value of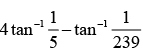
Ans:
Que 18: Show that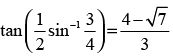 and justify why the other value
and justify why the other value
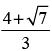 is ignored?
is ignored?
Ans:
To prove that[∴ tan (tan– 1 θ) = θ]
Que 19: If a1, a2, a3,...,an is an arithmetic progression with common difference d, then evaluate the following expression.
Ans:
If a1, a2, a3, ..., an are the terms of an arithmetic progression
∴ d = a2 – a1 = a3 – a2 = a4 – a3 ....
⇒ tan [tan-1 a2 - tan-1 a1 + tan-1 a3 tan-1 a2 + tan-1 a4 tan-1 a3 + ... + tan-1 an tan-1 an-1]
⇒ tan [tan-1 an tan-1 a1]
Objective Type Questions
Que 20: Which of the following is the principal value branch of cos–1x?
(a)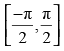
(b) (0, π )
(c) [0, π]
(d)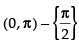
Ans: (c)
Sol:
Principal value branch of cos– 1 x is [0, π]. Hence the correct answer is (c).
Que 21: Which of the following is the principal value branch of cosec–1x?
(a)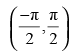
(b)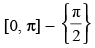
(c)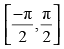
(d)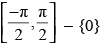
Ans: (d)
Sol:
Principal value branch of cosec– 1 x isas cosec– 1(0) = ∞ (not defined).
Hence, the correct answer is (d).
Que 22: If 3 tan–1 x + cot–1 x = π, then x equals
(a) 0
(b) 1
(c) – 1
(d) 1/2
Ans: (b)
Sol:
Given that 3 tan– 1 x + cot– 1 x = θ
⇒ 2 tan– 1 x + tan– 1 x + cot– 1 x = θ
∴ x = 1
Hence, the correct answer is (b).
Que 23: The value of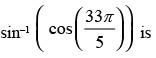
(a)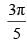
(b)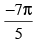
(c)
(d)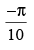
Ans: (d)
Sol:
Hence, the correct answer is (d).
Que 24: The domain of the function cos–1 (2x – 1) is
(a) [0, 1]
(b) [–1, 1]
(c) ( –1, 1)
(d) [0, π]
Ans: (a)
Sol:
The given function is cos– 1(2x – 1)
Let f(x) = cos– 1(2x – 1)
– 1 ≤ 2x – 1 ≤ 1 ⇒ - 1 + 1 ≤ 2x ≤ 1 + 1
0 ≤ 2x ≤ 2 ⇒ 0 ≤ x ≤ 1
∴ domain of the given function is [0, 1].
Hence, the correct answer is (a)
Que 25: The domain of the function defined by f (x) = sin–1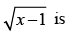
(a) [1, 2]
(b) [–1, 1]
(c) [0, 1]
(d) none of these
Ans: (a)
Sol:
Let
⇒ 0 ≤ x - 1 ≤ 1 ⇒ 1 ≤ x ≤ 2 ⇒ x ∈ [1, 2]
Hence, the correct answer is (a).
Que 26: If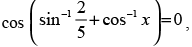 then x is equal to
then x is equal to
(a) 1/5
(b) 2/5
(c) 0
(d) 1
Ans: (b)
Sol:
Given that
⇒
⇒
⇒
⇒
Hence, the correct answer is (b).
Que 27: The value of sin (2 tan–1 (.75)) is equal to
(a) 0.75
(b) 1.5
(c) 0.96
(d) sin 1.5
Ans: (c)
Sol:
Given that sin [2 tan– 1 (0.75)]
= sin [sin– 1 (0.96)]
= 0.96
Hence, the correct answer is (c).
Que 28: The value of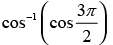 is equal to
is equal to
(a)2/π
(b)3π/2
(c)5π/2
(d)7π/2
Ans: (a)
Sol:
Hence, the correct answer is (a).
Que 29: The value of the expression 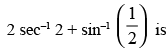
(a) π/6
(b) 5π/6
(c) 7π/6
(d) 1
Ans: (b)
Sol:
Hence, the correct answer is (b)
Que 30: If tan–1 x + tan–1y =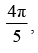 then cot–1 x + cot–1 y equals
then cot–1 x + cot–1 y equals
(a)π/ 5
(b)2π/ 5
(c)3π/5
(d) π
Ans: (a)
Sol:
Given that tan– 1 x + tan– 1 y =
Hence, the correct answer is (a).
Que 31: If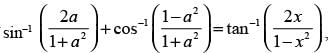 where a, x ∈ ]0, 1,
where a, x ∈ ]0, 1,
then the value of x is
(a) 0
(b) a/2
(c) a
(d)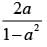
Ans. (d)
Sol:
⇒ 4 tan– 1 a = 2 tan– 1 x ⇒ 2 tan– 1 a = tan– 1 x
⇒
Hence, the correct answer is (d).
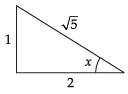
Que 32: The value of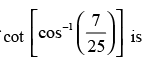
(a) 25/24
(b) 25/7
(c) 24/25
(d) 7/24
Ans: (d)
Sol:
We have,
Let
∴
Hence, the correct answer is (d).
Que 33: The value of the expression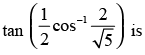
(a)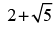
(b)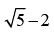
(c)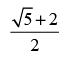
(d)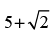
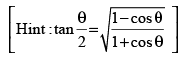
Ans. (b)
Sol:
We have,
Let
⇒
Hence, the correct answer is (b).
Que 34: If | x | ≤ 1, then 2 tan–1 x + sin–1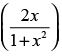 is equal to
is equal to
(a) 4 tan–1 x
(b) 0
(c) 2/π
(d) π
Ans. (a)
Sol:
Here, we have 2 tan-1 sin -1
Hence, the correct answer is (a).
Que 35: If cos–1 α + cos–1 β + cos–1 γ = 3π, then α (β + γ) + β (γ + α) + γ (α + β) equals
(a) 0
(b) 1
(c) 6
(d) 12
Ans. (c)
Sol:
We have cos–1 α + cos–1 β + cos–1 γ = 3π
⇒ cos–1 α + cos–1 β + cos–1 γ = π + π + π
⇒ cos–1 α = π, cos–1 β = π and cos–1 γ = π
⇒ α = cos π, β = cos π and γ = cos π
∴ α = – 1, β = – 1 and γ = – 1
Which gives a = β = γ = –1
So α (β + γ) + β( γ+ α) + γ(α + β)
⇒ (– 1)(– 1 – 1) + (– 1)(– 1 – 1) + (– 1)(– 1 – 1)
⇒ (– 1)(– 2) + (– 1)(– 2) + (– 1)(– 2) ⇒ 2 + 2 + 2 ⇒ 6
Hence, the correct answer is (c).
Q.36. The number of real solutions of the equation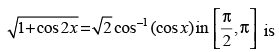
(a) 0
(b) 1
(c) 2
(d) infinite
Ans. (d)
Solution.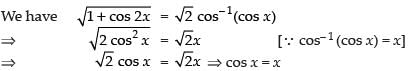
Which does not satisfy for any value of x.
Hence, the correct answer is (d).
Q.37. If cos–1x > sin–1x, then
(a)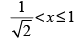
(b)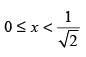
(c)
(d) x > 0
Ans. (c)
Solution.
Here, given that cos– 1 x > sin– 1 x
⇒ sin [cos– 1 x] > x
We know that – 1 ≤ x ≤ 1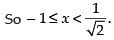
Hence, the correct answer is (c).
Fill in the blanks
Q.38. The principal value of is______.
is______.
Ans.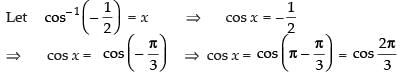
∴
Hence, Principal value of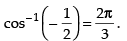
Q.39. The value of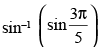 is_____.
is_____.
Ans.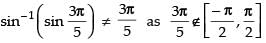
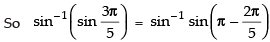
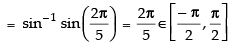
Hence, the value of 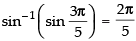
Q.40. If cos (tan–1 x + cot–1 √3 ) = 0, then value of x is_____.
Ans.
Given that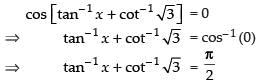

Hence, the value of x is √3 .
Q.41. The set of values of 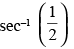 is_____.
is_____.
Ans.
Let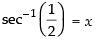 ⇒sec x =
⇒sec x =
Since, the domain of sec– 1 x is R – {– 1, 1} and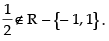
Hence, sec-1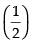 has no set of values.
has no set of values.
Q.42. The principal value of tan–1 √3 is_____.
Ans.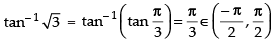
Hence the principal value of tan - 1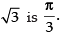
Q.43. The value of cos–1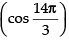 is_____.
is_____.
Ans.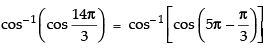
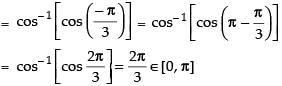
Hence, the value of cos-1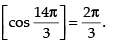
Q.44. The value of cos (sin–1 x + cos–1 x), |x| ≤ 1 is______ .
Ans.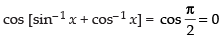
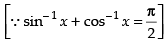
Hence, the value of cos (sin– 1 x + cos– 1 x) = 0.
Q.45. The value of expression tan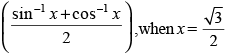
is______ .
Ans.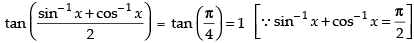
Hence, the value of the given expression is 1.
Q.46. If y = 2 tan–1 x + sin–1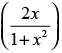 for all x, then____< y <____.
for all x, then____< y <____.
Ans.
⇒ y = 2 tan– 1 x + 2 tan– 1 x
⇒ y = 4 tan– 1 x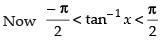
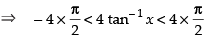 ⇒ – 2π < y < 2π
⇒ – 2π < y < 2π
Hence, the value of y is (– 2π, 2π).
Q.47. The result tan–1x – tan–1y = tan–1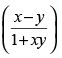 is true when value of xy is _____.
is true when value of xy is _____.
Ans.
The given result is true when xy > – 1.
Q.48. The value of cot–1 (–x) for all x ∈ R in terms of cot–1x is _______.
Ans.
cot–1(– x) = π – cot–1 x, x ∈ R [∵ as cot-1 (- x) = π - cot-1 x]
State True or False
Q.49. All trigonometric functions have inverse over their respective domains.
Ans.
False.
We know that all inverse trigonometric functions are restricted over their domains.
Q.50. The value of the expression (cos–1 x)2 is equal to sec2 x.
Ans.
False.
We know that cos–1 x = sec-1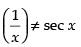
So (cos–1 x)2 ≠ sec2 x
Q.51. The domain of trigonometric functions can be restricted to any one of their branch (not necessarily principal value) in order to obtain their inverse functions.
Ans.
True.
We know that all trigonometric functions are restricted over their domains to obtain their inverse functions.
Q.52. The least numerical value, either positive or negative of angle θ is called principal value of the inverse trigonometric function.
Ans.
True.
Q.53. The graph of inverse trigonometric function can be obtained from the graph of their corresponding trigonometric function by interchanging x and y axes.
Ans.
True.
We know that the domain and range are interchanged in the graph of inverse trigonometric functions to that of their corresponding trigonometric functions.
Q.54. The minimum value of n for which tan–1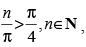
is valid is 5.
Ans.
False.
Given that
⇒
⇒ n > p ⇒ n > 3.14
Hence, the value of n is 4.
Q.55. The principal value of sin–1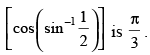
Ans.
True.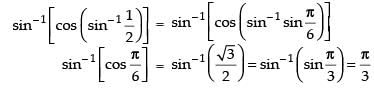
|
172 videos|503 docs|154 tests
|
FAQs on NCERT Exemplar: Inverse Trigonometric Functions - Mathematics (Maths) for JEE Main & Advanced
| 1. What are the principal values of inverse trigonometric functions? |  |
| 2. How do you derive the formulas for inverse trigonometric functions? |  |
| 3. What is the relationship between inverse trigonometric functions and their corresponding trigonometric functions? |  |
| 4. How can we simplify expressions involving inverse trigonometric functions? |  |
| 5. What are the applications of inverse trigonometric functions in real-life problems? |  |