MULTIPLE CHOICE QUESTIONS I
Q.1. Modulus of rigidity of ideal liquids is
(a) Infinity
(b) Zero
(c) Unity
(d) Some finite small non-zero constant value
Ans. (b)
Solution.
Modulus of Rigidity: Within limits of proportionality, the ratio of tangential stress to the shearing strain is called modulus of rigidity of the material of the body and is denoted by η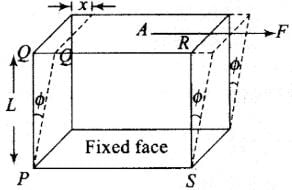
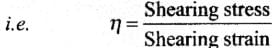
In this case the shape of a body changes but its volume remains unchanged.
Consider a cube of material fixed at its lower face and acted upon by a tangential force F at its upper surface having area A.
Only solids can exhibit a shearing as these have definite shape.
In liquids,η = 0
So, the frictional (viscous) force cannot exist in case of ideal fluid and since they cannot sustain shearing stress or tangential forces are zero, so there is no stress developed.
Q.2. The maximum load a wire can withstand without breaking, when its length is reduced to half of its original length, will
(a) Be double
(b) Be half
(c) Be four times
(d) Remain same
Ans. (d)
Solution.
When the wire is loaded beyond the elastic limit, then strain increases much more rapidly. The maximum stress corresponding to B (see stress—strain curve) after which the wire begin to flow and breaks, is called breaking stress or tensile strength and the force by application of which the wire breaks is called the breaking force.
(i) Breaking force depends upon the area of cross-section of the wire, i.e. Breaking force ∝ A
Breaking force = P x A
Here P is a constant of proportionality and known as breaking stress.
(ii) Breaking stress is a constant for a given material and it does not depend upon the dimension (length or thickness) of wire.
(iii) If a wire of length L is cut into two or more parts, then again its each part can hold the same weight as breaking force is independent of the length of wire.
Q.3. The temperature of a wire is doubled. The Young’s modulus of elasticity
(a) Will also double
(b) Will become four times
(c) Will remain same
(d) Will decrease
Ans. (d)
Solution.
Youngs modulus (Y)
It is defined as the ratio of normal stress to longitudinal strain within limit of proportionality.
The fractional change in length of any material is defined as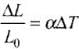
where ΔT is change in the temperature, L0 is original length, ∝ is the coefficient of linear expansion of the given material and L0 is the original length of material.
So, simply change in length is due to change in temperature.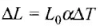
And Young's modulus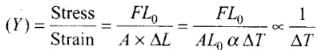
As Y ∝ 1/ ∆T
When temperature increases ∆T increases, hence Y decreases.
Q.4. A spring is stretched by applying a load to its free end. The strain produced in the spring is
(a) Volumetric
(b) Shear
(c) Longitudinal and shear
(d) Longitudinal.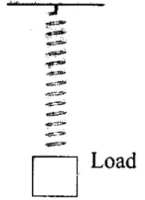
Ans. (c)
Solution.
According to the diagram where a spring is suspended with a fixed rigid support. Now a load is attached with the lower end of that spring. So, it is stretched by applying a load to its free end. Clearly the length and shape of the spring changes and the weight of the load behaves as a deforming force.
The change in length corresponds to longitudinal strain and change in shape corresponds to shearing strain.
Q.5. A rigid bar of mass M is supported symmetrically by three wires each of length l . Those at each end are of copper and the middle one is of iron. The ratio of their diameters, if each is to have the same tension, is equal to
(a) Ycopper/Yiron
(b)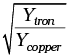
(c) 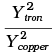
(d) 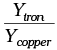
Ans. (b)
Solution.
As the bar is supported symmetrically by the three wires, therefore extension in each wire is same.
Let T be the tension in each wire and diameter of the wire is D, then Young’s modulus is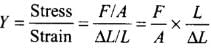
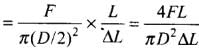
⇒ 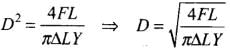
As F and 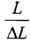 are constants.
are constants.
Hence, 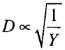
or 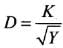 (K is the proportionality constant)
(K is the proportionality constant)
Now, We can find ratio as 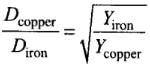
Q.6. A mild steel wire of length 2L and cross-sectional area A is stretched, well within elastic limit, horizontally between two pillars (Figure). A mass m is suspended from the mid point of the wire. Strain in the wire is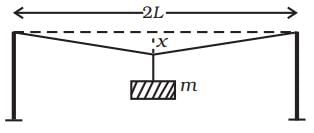 (a)
(a)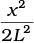
(b) x/L
(c) x2/L
(d) x2/2L
Ans. (a)
Solution.
We will assume the vertical displacement x to be very small compared to L. Change in the length will be calculated by difference of final total length and initial length 2L.
According to the diagram: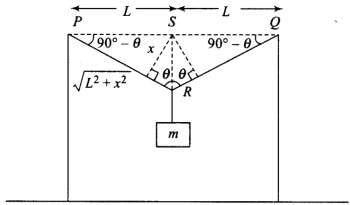
Hence, change in length
ΔL = (PR + RQ) - PQ
= 2 PR - PQ (∵ PR = PQ)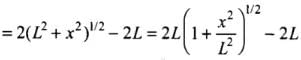
By binomial theorem, we get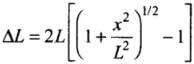
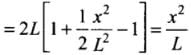 [ ∵ x << L]
[ ∵ x << L]
∴ 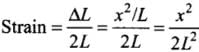
Q.7. A rectangular frame is to be suspended symmetrically by two strings of equal length on two supports (Figure). It can be done in one of the following three ways;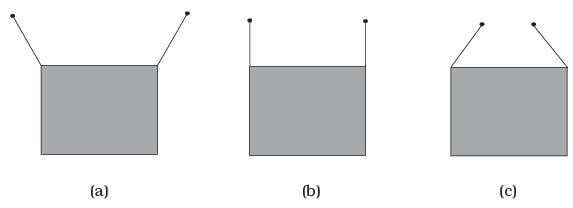 The tension in the strings will be
The tension in the strings will be
(a) The same in all cases
(b) Least in (a)
(c) Least in (b)
(d) Least in (c)
Ans. (c)
Solution.
According to the FBD diagram of the rectangular frame. Let M be the mass of rectangular frame and 0be the angle which the tension T in the string makes with the horizontal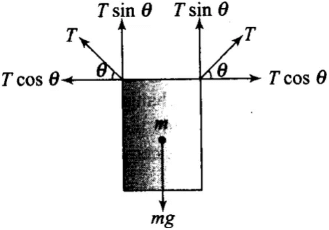
Balancing vertical forces,
2T sin θ - mg = 0 [T is tension in the string]
⇒ 2T sin θ = mg ...(i)
Total horizontal force will be zero because of equal and opposite forces balance each other (T cos θ).
Now from Eq. (i) 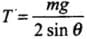
Here, we know mg is constant.
⇒ 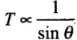
Here, we know mg is constant.
⇒ 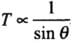
T is least if sin θ has maximum value.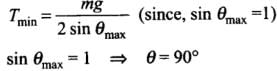
So the correct option is option (c).
Hence, tension is least for the case (b).
Q.8. Consider two cylindrical rods of identical dimensions, one of rubber and the other of steel. Both the rods are fixed rigidly at one end to the roof. A mass M is attached to each of the free ends at the centre of the rods.
(a) Both the rods will elongate but there shall be no perceptible change in shape.
(b) The steel rod will elongate and change shape but the rubber rod will only elongate.
(c) The steel rod will elongate without any perceptible change in shape, but the rubber rod will elongate and the shape of the bottom edge will change to an ellipse.
(d) The steel rod will elongate, without any perceptible change in shape, but the rubber rod will elongate with the shape of the bottom edge tapered to a tip at the centre
Ans. (d)
Solution.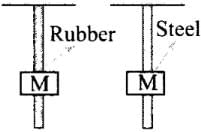
According to the diagram shown below in which a mass AT is attached at the centre of each rod, then both rods will be elongated. But due to different elastic properties of material the steel rod will elongate without making any perceptible change in shape, but the rubber rod will elongate with the shape of the bottom edge tapered to a tip at the centre.
MULTIPLE CHOICE QUESTIONS II
Q.9. The stress-strain graphs for two materials are shown in Figure (assume same scale).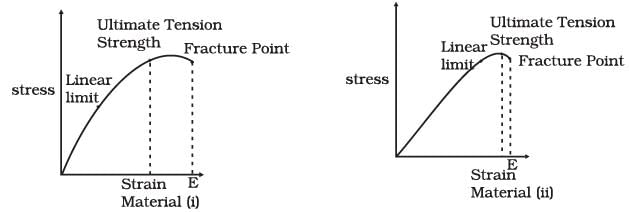 (a) Material (ii) is more elastic than material (i) and hence material (ii) is more brittle
(a) Material (ii) is more elastic than material (i) and hence material (ii) is more brittle
(b) Material (i) and (ii) have the same elasticity and the same brittleness
(c) Material (ii) is elastic over a larger region of strain as compared to(i)
(d) Material (ii) is more brittle than material (i)
Ans. (c, d)
Solution.
Representation of different points on Stress-Strain graph: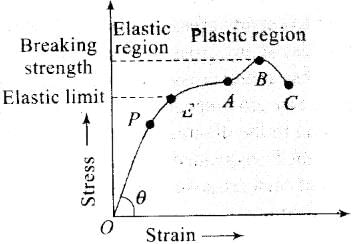
When the strain is small (< 2%) (i.e., in region OP) stress is proportional to strain. This is the region where the so called Hooke’s law is obeyed. The point P is called limit of proportionality and slope of line OP gives the Young’s modulus Y of the material of the wire. If 6is the angle of OP from strain axis, then Y= tan θ.
If the strain is increased a little bit, i.e. in the region PE, the stress is not proportional to strain. However, the wire still regains its original length after the removal of stretching force.
This behaviour is shown up to point E known as elastic limit or yield- point. The region OPE represents the elastic behaviour of the material of wire.
If the wire is stretched beyond the elastic limit E, i.e. between EA, the strain increases much more rapidly and if the stretching force is removed the wire does not come back to its natural length. Some permanent increase in length takes place.
If the stress is increased further by a very small increase in it a very large increase in strain is produced (region AB) and after reaching point B, the strain increases even if the wire is unloaded and ruptures at C. In the region BC the wire literally flows. The maximum stress corresponding to B after which the wire begins to flow and breaks is called breaking or tensile strength. The region EABC represents the plastic behaviour of the material of wire.
Material having more ultimate tensile strength will be elastic over larger region.
So, from graph (i) linear limit vanishes soon and for small stress there is large strain as compared to graph (ii).
Hence, material (ii) is more elastic over a large region of strain as compared to (i). So, the ultimate tensile strength for material (ii) is greater than (i).
A material is said to be more brittle if its fracture point is more closer to ultimate strength point.
Hence material (ii) is more brittle than material (i).
Q.10. A wire is suspended from the ceiling and stretched under the action of a weight F suspended from its other end. The force exerted by the ceiling on it is equal and opposite to the weight
(a) Tensile stress at any cross section A of the wire is F/A
(b) Tensile stress at any cross section is zero
(c) Tensile stress at any cross section A of the wire is 2F/A
(d) Tension at any cross section A of the wire is F
Ans. (a, d)
Solution.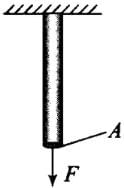
According to the diagram a wire is stretched under the j
action of a weight F suspended from its other end.
Clearly, forces at each cross-section is F.
Now applying formula,
Tensile stress = Force applied/Area of cross-section = F/A
Tension = Applied force = F
Q.11. A rod of length l and negligible mass is suspended at its two ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths (Figure). The cross-sectional areas of wires A and B are 1.0 mm2 and 2.0 mm2, respectively.
(YAl = 70 x 109 Nm-2 and Ysteel 200 x 109 Nm –2 ) (a) Mass m should be suspended close to wire A to have equal stresses in both the wires
(a) Mass m should be suspended close to wire A to have equal stresses in both the wires
(b) Mass m should be suspended close to B to have equal stresses in both the wires
(c) Mass m should be suspended at the middle of the wires to have equal stresses in both the wires
(d) Mass m should be suspended close to wire A to have equal strain in both wires
Ans. (b, d)
Solution.
According to the diagram a massless rod is suspended at its two ends by two wires of steel (wire A) and aluminum (wire B) of equal lengths.
Let the mass is suspended at x from the end B, which develop equal stress in wires.
Let Ta and TB be the tensions in wire A and wire B respectively.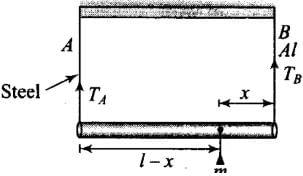
Stress in steel wire A, 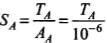
Stress in Al wire, 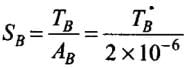
where AA and AB are cross-sectional areas of wire A and B respectively. Also, from rotational equilibrium , net torque is zero, i.e. TBX - TA(l - x ) = 0
⇒ 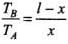
For equal stress, SA = SB
⇒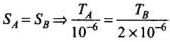
⇒ 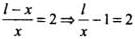
⇒ 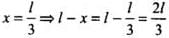
Hence, mass m should be suspended close to wire B (Al wire).
We know, Strain =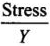
So, for equal strain in the wires,
⇒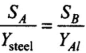
⇒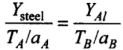
⇒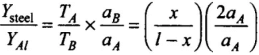
⇒ 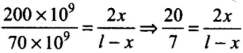
⇒ 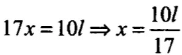
⇒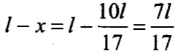
Hence, mass m should be suspended close to wire A (steel wire).
Q.12. For an ideal liquid
(a) The bulk modulus is infinite
(b) The bulk modulus is zero
(c) The shear modulus is infinite
(d) The shear modulus is zero
Ans. (a, d)
Solution.
Bulk Modulus: When a solid or fluid (liquid or gas) is subjected to a uniform pressure all over the surface, such that the shape remains the same, then there is a change in volume.
Then the ratio of normal stress to the volumetric strain within the elastic limits is called as Bulk modulus. This is denoted by K.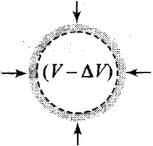
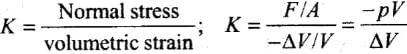
where p = increase in pressure; V= original volume; ∆V= change in volume The negative sign shows that with increase in pressure p, the volume decreases by ∆ V, i.e. if p is positive, ∆V is negative. The reciprocal of bulk modulus is called compressibility.
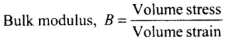
As an ideal liquid is not compressible. Hence, change in volume, ∆V= 0
It means volume strain is zero.
Bulk modulus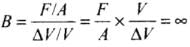
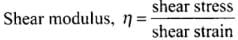
A liquid cannot sustain tangential force. It may contain tangential viscous drag, so, η = 0.
Q.13. A copper and a steel wire of the same diameter are connected end to end. A deforming force F is applied to this composite wire which causes a total elongation of 1 cm. The two wires will have
(a) The same stress
(b) Different stress
(c) The same strain
(d) Different strain
Ans. (a, d)
Solution.
According to the diagram where a deforming force F is applied to the combination.
Ysteel = Stress/ Strain = F/A/Strain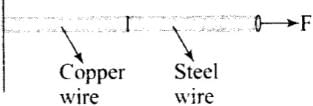 Ysteel ≠ Ycopper
Ysteel ≠ Ycopper
(a) Stress = F/ A
So stress in the wire depends upon cross sectional area and deforming force, if force and area both are same then stress remains same.
(b) Because of having different young’s modulus, the two wires will have different strain.
VERY SHORT ANSWER TYPE QUESTIONS
Q.14. The Young’s modulus for steel is much more than that for rubber. For the same longitudinal strain, which one will have greater tensile stress?
Ans. 
For same longitudinal strain. Young's modulus is proportional to tensile stress, i.e., Y ∝ stress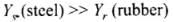
∴  ...(i)
...(i)
∴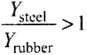
Therefore, from Eq. (i).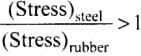
⇒ (Stress)steel, > (Stress)rubber
Hence, for same longitudinal strain, steel will have greater tensile stress than that of rubber.
Q.15. Is stress a vector quantity ?
Ans. Stress = Magnitude of internal reaction force / Area of cross-section
Hence, stress is not a scalar quantity not a vector quantity, it is a tensor quantity.
Q.16. Identical springs of steel and copper are equally stretched. On which, more work will have to be done?
Ans. Work Done in stretching a Wire or Spring:
In stretching a wire work is done against internal restoring forces. This work is stored in the wire as elastic potential energy or strain energy.
If a force F acts along the length L of the wire of cross-section A and stretches it by x, then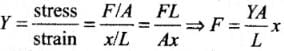
So the work done for an additional small increase dx in length,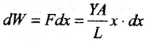
Hence the total work done in increasing the length by l,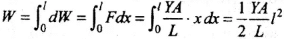
This work done is stored in the wire.
According to this problem work done in stretching a wire is given by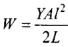
As springs of steel and copper are equally stretched. Therefore, for same force (F),
W ∝Δl ...(i)
As both springs are identical, so A and L are same.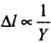
From Eqs. (i) and (ii), we get W ∝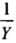
∴ 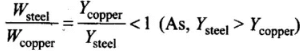
⇒ 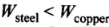
Hence, more work will be done in case of spring made of copper.
Q.17. What is the Young’s modulus for a perfect rigid body ?
Ans. According to Hooke’s law
For a perfectly rigid body, change in length Δl = 0, therefore longitudinal strain is zero.
∴ 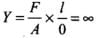
Hence, Young’s modulus for a perfectly rigid body is infinite (∞).
Q.18. What is the Bulk modulus for a perfect rigid body ?
Ans. Bulk modulus is given by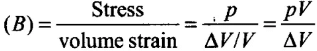
For perfectly rigid body, change in volume AV = 0, therefore volumetric strain is zero.
∴ 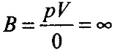
Hence, bulk modulus for a perfectly rigid body is infinity
SHORT ANSWER TYPE QUESTIONS
Q.19. A wire of length L and radius r is clamped rigidly at one end. When the other end of the wire is pulled by a force f, its length increases by l. Another wire of the same material of length 2L and radius 2r, is pulled by a force 2f. Find the increase in length of this wire.
Ans. We have to apply Hooke’s law to compare the extension in each wire. According to the diagram which shows the situation.
Now, Young’s modulus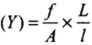
First case,
length of wire = L, radius of wire = r
Force applied = f, increase in length = l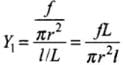 ...(i)
...(i)
In second case,
length of wire = 2L, radius of wire = 2r,
force applied = 2f, increase in length = x (say)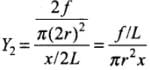 ...(ii)
...(ii)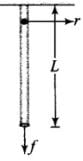
Both the wires are of same material, so Young's modulus will be same.
From Eqs. (i) and (ii),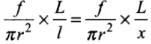
Hence, x = l.
Q.20. A steel rod (Y = 2.0 × 1011 Nm–2; and α = 10–50 C–1) of length 1 m and area of cross-section 1 cm2 is heated from 0°C to 200°C, without being allowed to extend or bend. What is the tension produced in the rod?
Ans. As the temperature of the rod increases, length increases. The equation of thermal expansion for linear expansion will be applied.
According to the problem. Young’s modulus of steel Y = 2.0 x 1011 N/m2
Coefficient of thermal expansion α = 10-5 ºC-1
Length L= I m
Area of cross-section A =1 cm2 = 1 x 10-4 m2
Rise in temperature Δt = 200°C - 0°C = 200°C
A = 1 cm2 = 10-4 m2, ΔT = 200°C - 0°C = 200°C
∴ ΔL = ∝LΔT = 10-5 x 1 x 200 = 2 x 10-3 m
Let the tension produced in rod by the compression is T.
∴ 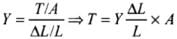
⇒ 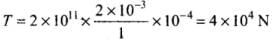
Q.21. To what depth must a rubber ball be taken in deep sea so that its volume is decreased by 0.1%. (The bulk modulus of rubber is 9.8×108 N m–2; and the density of sea water is 103 kg m–3.)
Ans. According to the problem, Bulk modulus of rubber (B) = 9.8 x 108 N/m2 Density of sea water (p) = 103 kg/m3 Percentage decrease in volume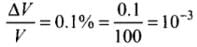
ρ = 103 kg m-3 h = ?
Let the rubber ball be taken up to depth h.
∴ Change in pressure (p) = hρg
We Know, 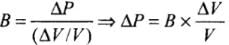
⇒ 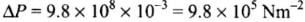
Also, ΔP = ρgh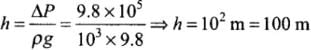
Q.22. A truck is pulling a car out of a ditch by means of a steel cable that is 9.1 m long and has a radius of 5 mm. When the car just begins to move, the tension in the cable is 800 N. How much has the cable stretched? (Young’s modulus for steel is 2 × 1011 Nm–2.
Ans. According to the problem,
Length of steel cable l = 9.1 m
Radius r = 5 mm = 5 x 10~3 m
Tension in the cable F = 800 N
Young’s modulus for steel Y= 2 x 1011 N/m2
Change in length ∆l = ?
Young's modulus if given by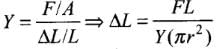
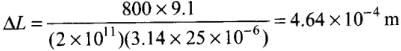
⇒ 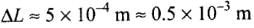
Q.23. Two identical solid balls, one of ivory and the other of wet-clay, are dropped from the same height on the floor. Which one will rise to a greater height after striking the floor and why?
Ans. Since, ivory ball is more elastic than wet-clay ball, therefore, it tends to regain its original shape quickly. Due to this reason, more energy and momentum is transferred to the ivory ball in comparison to the wet-clay ball and hence, ivory ball will rise higher after striking the floor even though both are dropped from the same height.
LONG ANSWER TYPE QUESTIONS
Q.24. Consider a long steel bar under a tensile stress due to forces F acting at the edges along the length of the bar (Figure). Consider a plane making an angle θ with the length. What are the tensile and shearing stresses on this plane?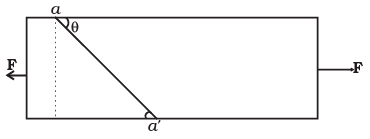 (a) For what angle is the tensile stress a maximum?
(a) For what angle is the tensile stress a maximum?
(b) For what angle is the shearing stress a maximum?
Ans. According to the problem force F is applied along horizontal, so we resolve it in two perpendicular components—one is parallel to the inclined plane and other one is perpendicular to the inclined plane as shown in the diagram. Now, we can easily calculate the tensile and shearing stress. Here,
F⊥ = F sin θ, F║ - F cos θ
Let the cross-sectional area of the bar be A. Consider the equilibrium of the plane aa' . Here, F⊥ produces tensile stress and F║ , produces shear stress, on the plane aa'.
Let the area of the face aa' be A , then
∴ 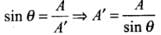
Tensile stress on the plane aa'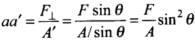
Shearing stress on the plane aa',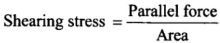
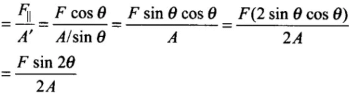
(a) For tensile stress to be maximum,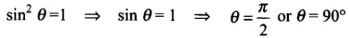
(b) For shearing stress to be maximum,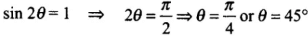
Important point: Here we are not applying direct formula for stress. Because to analyze different types of stresses, we have to divide the force in components. In normal stress, the force is applied normal to the surface. But in shear stress deforming force is applied tangential to one of the faces
Q.25. (a) A steel wire of mass µ per unit length with a circular cross section has a radius of 0.1 cm. The wire is of length 10 m when measured lying horizontal, and hangs from a hook on the wall. A mass of 25 kg is hung from the free end of the wire. Assuming the wire to be uniform and lateral strains << longitudinal strains, find the extension in the length of the wire. The density of steel is 7860 kg m–3 (Young’s modules Y=2×1011 Nm–2).
(b) If the yield strength of steel is 2.5×108 Nm–2, what is the maximum weight that can be hung at the lower end of the wire?
Ans. Consider an small element dx, of mass dm from length L of wire at distance X. from the end of hung weight. µ is mass per unit length
dm = µ.dx r = 0.1cm = 0.1 x 10-2 m= 10-3 m
A = πr2 = π(10)-6 M =25kg; L = 10m
(a) downward force on dx= ωt below it (dx)
T(x) = (x./u)g+Mg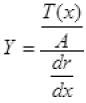
Where dr is increase in length of wire by T(x)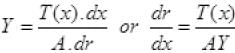
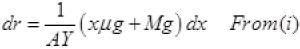
Integrating both sides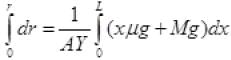
r(change in length L) = 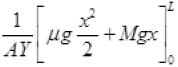
extension in wire of length L = 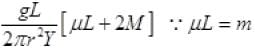
m the whole mass of wire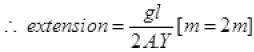
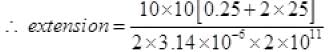
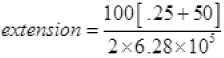
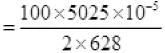
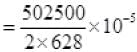
= 400 x 10-5 m
Extension = 4.00x10-3 m
m = vol x density
= (A.L)x P
= πr2 x 10 x 7860
= 3.14 x (10-3)2 x 7860 x 10
= 3.14 x (7860) x 10-6 x 10
= 3.14 x 786 x 10-4 kg
= 2468.04 x 10-4 kg
m ≅ 0.25 kg
(b) Tension in the wire will be maximum at x = L
T(x) = μgx + Mg
T(L) = μgL+Mg
T = μLg+Mg (∵ μL=m)
∴ T = (m+M)g
Yield force = [Yield strength (Y)]x A
= 2.5 x 108 x 3.14 x 10-6
Yield force = 250 x 3.14
Yield force = Tension (maximum)
250 x 3.14= (m+M)g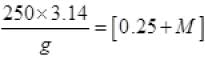
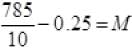
M = 78.5 - 0.25
M= 78.25 Kg.
Q.26. A steel rod of length 2l, cross sectional area A and mass M is set rotating in a horizontal plane about an axis passing through the centre. If Y is the Young’s modulus for steel, find the extension in the length of the rod. (Assume the rod is uniform.)
Ans. First we have to consider a small element on the rod of mass dm to find tension in the rod at this element and then calculate for the whole rod.
Let us consider an element of width dx at a distance x from the given axis of rotation as shown in the diagram.
As we know the rod is uniform, so mass per unit length, 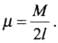
Mass of small element dm = 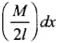
Centripetal force acting on this clement,
dF = dm . xω2
⇒ 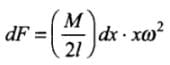
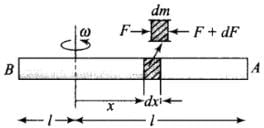 Here, dF is provided by tension n in clement dx of the rod due to x elasticity.
Here, dF is provided by tension n in clement dx of the rod due to x elasticity.
Let tension in the rod be F at a distance x from the axis of rotation.
F is due to centripetal force acting on all the elements from x to l, i.e.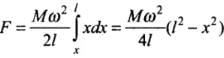
If d(r) is the extension in the element of length dx at position x. then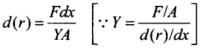
Hence, extension in the half of the rod (from axis to point A) is given by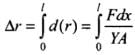
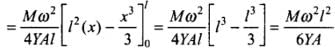
Hence, total extension in entire rod of length 2l.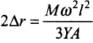
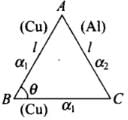
∴ Total change in length = 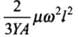
Q.27. An equilateral triangle ABC is formed by two Cu rods AB and BC and one Al rod. It is heated in such a way that temperature of each rod increases by ∆T. Find change in the angle ABC. [Coeff. of linear expansion for Cu is α1, Coeff. of linear expansion for Al is α2 ]
Ans. As the temperature of the rods increases length of each side will change, hence the angle corresponding to any vertex also changes as shown in the diagram.
Before heating, AB = BC = CA = l
After heating temperature of each rod is changed by ∆T and sides of ∆ABC is changed.
Let AB = l1,BC = l3,CA = l2 Using cosine formula,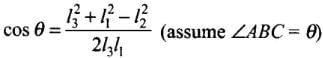
⇒ 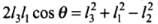
On differentiating the above expression we get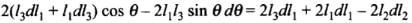
Here, 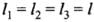 (as it is an equilateral triangle)
(as it is an equilateral triangle)
Now, 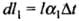 (where. Δt = change in temperature)
(where. Δt = change in temperature)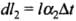
and 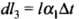
therefore, 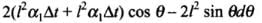
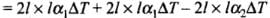
Dividing it by 2l2, we get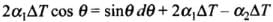
⇒ 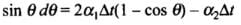
Substituting, θ= 60° (for equilateral triangle)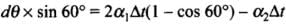
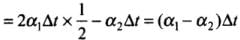
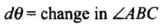
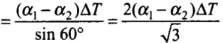 (∵Δt = ΔT given)
(∵Δt = ΔT given)
Q.28. In nature, the failure of structural members usually result from large torque because of twisting or bending rather than due to tensile or compressive strains. This process of structural breakdown is called buckling and in cases of tall cylindrical structures like trees, the torque is caused by its own weight bending the structure. Thus the vertical through the centre of gravity does not fall within the base. The elastic torque caused because of this bending about the central axis of the tree is given by 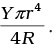 Y is the Young’s modulus, r is the radius of the trunk and R is the radius of curvature of the bent surface along the height of the tree containing the centre of gravity (the neutral surface). Estimate the critical height of a tree for a given radius of the trunk.
Y is the Young’s modulus, r is the radius of the trunk and R is the radius of curvature of the bent surface along the height of the tree containing the centre of gravity (the neutral surface). Estimate the critical height of a tree for a given radius of the trunk.
Ans. According to the problem, the elastic torque or the bending torque is given and we have to find the torque caused by the weight due to bending.
The diagram of the given situation is as shown.
The bending torque on the trunk of radius r of tree = YπR4/4R
where R the radius of curvature of the bent surface.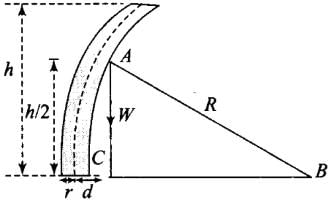
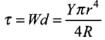
Here deforming torque is equal to elastic torque (restoring torque) caused by bending of tree about its central axis when the tree is about to buckle.
Let h be the height of tree. If R >> h, then the centre of gravity of tree is at a height h/2 from the ground.
Refer figure, in ΔABC
R2 = (R - d)2 + (h/2)2 = R2 - 2Rd + d2 + h2/4
Since, d << R, therefore the term d2 being very very small can be neglected.
R2 = R2 - 2 Rd + h2/d
or 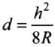 ...(i)
...(i)
If ω0 is the weight/volume, then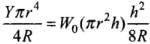 [ ∵ Torque is caused by the weight]
[ ∵ Torque is caused by the weight]
⇒ 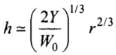
Hence, critical height = h =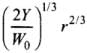
Q.29. A stone of mass m is tied to an elastic string of negligible mass and spring constant k. The unstretched length of the string is L and has negligible mass. The other end of the string is fixed to a nail at a point P. Initially the stone is at the same level as the point P. The stone is dropped vertically from point P.
(a) Find the distance y from the top when the mass comes to rest for an instant, for the first time.
(b) What is the maximum velocity attained by the stone in this drop?
(c) What shall be the nature of the motion after the stone has reached its lowest point?
Ans. (a) It is clear from question that Ball will at least travel to natural length of spring and further it will stretch due its elastic nature of spring.
Let assume that distance travelled by stone of Mass = x
Now we know that it isn’t elastic collision, therefore Energy will conserve. By travelling a distance of Y it will gain Potential energy of spring which will store in spring whereas it will lose its potential energy.
Therefore loss in Potential energy = M* g * x
And gain in Potential energy of spring 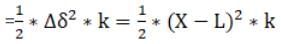
Here we taking the difference as energy is gained by spring is for the extra distance it will travel from its natural length.
Equating both equations 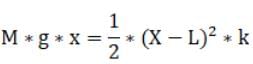
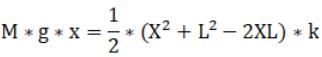
Solving the quadratic equation we will get two solutions, the solution with positive will answer as we are dealing in positive domain of distance. 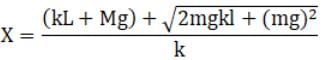
(b) Maximum will be attained when a particle isn’t experiencing any force. That is when a particle’s own gravitational force is equal to force due to elasticity of spring
mg = kp
Where p is distance from its natural length (No force is experienced before spring stretches out of its natural length)
Using Conservation of energy, we know that loss in potential energy will be gain in kinetic energy which will be gain by particle and gain in elastic energy of spring. 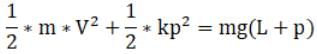
Equating p to, 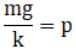
And solving the quadratic equation and taking only positive sign for velocity as we dealing in positive domain, we get, 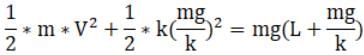
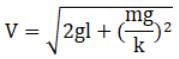
(c) Intuitively we know that particle will perform SHM, but we need to prove that. Therefore we need to reduce it to SHM equation.
We know that at particular distance y (from its initial position) we can write, 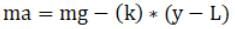
As the FNet which will experienced by stone will due to gravitational force towards down and elastic force towards up. And we also know that acceleration is double derivative of distance travel therefore we can write,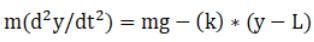
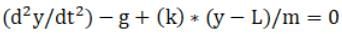
To reduce more, we will assume that 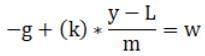
Now double differentiating w w.r.t time we will get, 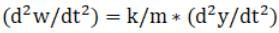
Substituting in above equation we get, 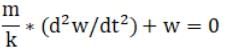
Therefore, its angular frequency is 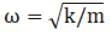
For calculating its mean position we have to find a particular distance at which no force is acting, 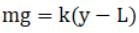
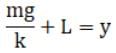
FAQs on NCERT Exemplar: Mechanical Properties of Solids - JEE
| 1. What are the mechanical properties of solids? |  |
| 2. What is elasticity and how is it measured? |  |
| 3. What is plasticity and how does it differ from elasticity? |  |
| 4. What is strength and how is it determined? |  |
| 5. What is hardness and how is it measured? |  |


















