NCERT Exemplar: Motion | Science Class 9 PDF Download
Multiple Choice Questions
Q1. A particle is moving in a circular path of radius r. The displacement after half a circle would be:
(a) Zero
(b) πr
(c) 2r
(d) 2πr
Ans: (c) 2r
Explanation: After half revolution,
Distance travelled = X, circumference= πr,
Displacement = Final position- Initial Position
It comes out to be the diameter of the circle = 2R.
Q2. A body is thrown vertically upward with velocity u, the greatest height h to which it will rise is,
(a) u/g
(b) u2/2g
(c) u2/g
(d) u/2g
Ans: (b) u2/2g
Explanation: v2 = u2+ 2as, here v = 0, a = -g, s = H
0 = u² - 2gH ⇒ H = u²/2g
Q3. The numerical ratio of displacement to distance for a moving object is:
(a) always less than 1
(b) always equal to 1
(c) always more than 1
(d) equal or less than 1
Ans: (d) equal or less than 1
Explanation: The shortest distance between the initial and the endpoint is called displacement whereas Distance is the total path length. Displacement is vector and it may be positive or negative whereas Distance is scalar and it can never be negative. The distance can be equal or greater than displacement which means the ratio of displacement to distance is always equal to or less than 1.
Q4. If the displacement of an object is proportional to square of time, then the object moves with
(a) uniform velocity
(b) uniform acceleration
(c) increasing acceleration
(d) decreasing acceleration
Ans: (b) uniform acceleration
Explanation: Velocity is measured in distance per second and acceleration is measured in Distance per second square. Hence Uniform acceleration is the right answer.
Q5. From the given v – t graph, it can be inferred that the object is
(a) in uniform motion
(b) at rest
(c) in non-uniform motion
(d) moving with uniform acceleration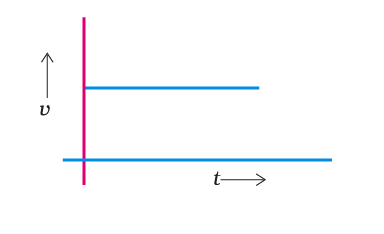 Ans: (a) in uniform motion
Ans: (a) in uniform motion
Explanation: From the above-given graph, it is clear that the velocity of the object remains constant throughout, hence the object is in uniform motion.
Q6. Suppose a boy is enjoying a ride on a merry-go-round which is moving with a constant speed of 10 m/s. It implies that the boy is:
(a) at rest
(b) moving with no acceleration
(c) in accelerated motion
(d) moving with uniform velocity
Ans: (c) in accelerated motion
Explanation: The boy is moving in a circular motion and circular motion is an accelerated motion hence (c) is the right answer.
Q7. Area under a v – t graph represents a physical quantity which has the unit:
(a) m2
(b) m
(c) m3
(d) ms–1
Ans: (b) m
Explanation: The area given in the graph represents Displacement and its unit is meter. Hence the answer is (b) m
Q8. Four cars A, B, C and D are moving on a levelled road. Their distance versus time graphs are shown in Fig. 8.2. Choose the correct statement:
(a) Car A is faster than car D.
(b) Car B is the slowest.
(c) Car D is faster than car C.
(d) Car C is the slowest.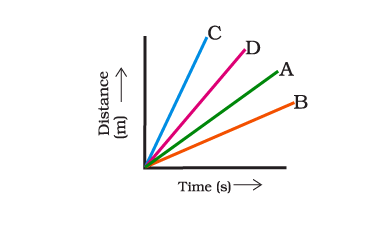 Ans: (b) Car B is the slowest.
Ans: (b) Car B is the slowest.
Explanation: The graph shows that Car B covers less distance in a given time than A, C and D cars hence it is the slowest.
Q9. Which of the following figures represents the uniform motion of a moving object correctly?
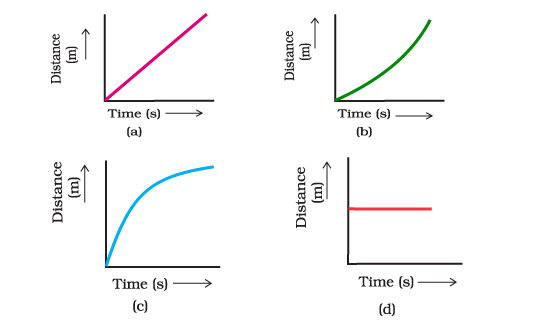 Ans: (a)
Ans: (a)
Explanation: Distance in graph a) is uniformly increasing with time hence it represents uniform motion.
Q10. Slope of a velocity-time graph gives:
(a) the distance
(b) the displacement
(c) the acceleration
(d) the speed
Ans: (c) the acceleration
Explanation: The slope of a velocity-time graph represents acceleration because it shows the rate of change of velocity with respect to time.
Q11. In which of the following cases of motions, the distance moved and the magnitude of displacement are equal?
(a) If the car is moving on a straight road
(b) If the car is moving in a circular path
(c) The pendulum is moving to and fro
(d) The earth is revolving around the Sun
Ans: (a) If the car is moving on a straight road
Explanation: In other cases given here displacement can be less than distance hence option (a) is the right answer.
Short Answer Type Questions
Q12. The displacement of a moving object in a given interval of time is zero. Would the distance travelled by the object also be zero? Justify your answer.
Ans: No, the object might have travelled some distance, provided the initial position and final position of the body coincide. Zero Displacement
Zero Displacement
Q13. How will the equations of motion for an object moving with a uniform velocity change?
Ans: When an object travels with uniform velocity then v = u and a = 0.
∴ v = u + at ⇒ v = u
s = ut + (1/2) at2 = ut
v2 = u2 + 2as ⇒ v2 = u2
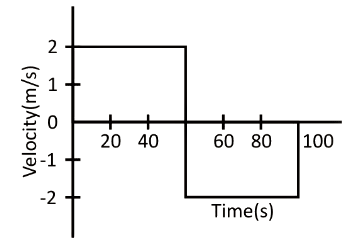
Q14. A girl walks along a straight path to drop a letter in the letterbox and comes back to her initial position. Her displacement-time graph is shown in the figure. Plot a velocity-time graph for the same.
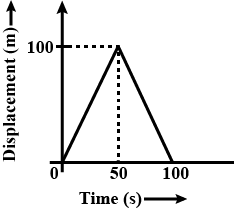 Ans:
Ans:
Q15. A car starts from rest and moves along the x-axis with constant acceleration of 5 ms-2 for 8 seconds. It then continues with constant velocity. What distance will the car cover in 12 seconds since it started from rest?
Ans: u = 0, a = 5 ms-2, t = 8 s.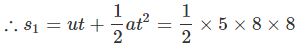 = 160 m (for first 8 s)
= 160 m (for first 8 s)
Velocity at the end of 8s, v = u + at = 0 + 5 x 8 = 40 ms-1
∴ s2 - vt = 40 x 4 = 160 m (for last 4 s)
Total distance = s1 + s2 = 160 m + 160 m = 320 m
Q16. A motorcyclist drives from A to B with a uniform speed of 30 km/h-1 and returns back with a speed of 20 km/h-1. Find its average speed.
Ans: Let distance travelled from A to B = S km
∴ Total distance = x + x = 2x.
Time taken to travel from A to B = t1 =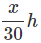
Time taken to travel from B to A = t2 = 
Total time, 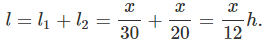
Average speed =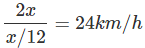
Q17. The velocity-time graph (Fig. 8.5) shows the motion of a cyclist.
Find (i) its acceleration (ii) its velocity and (iii) the distance covered by the cyclist in 15 seconds.
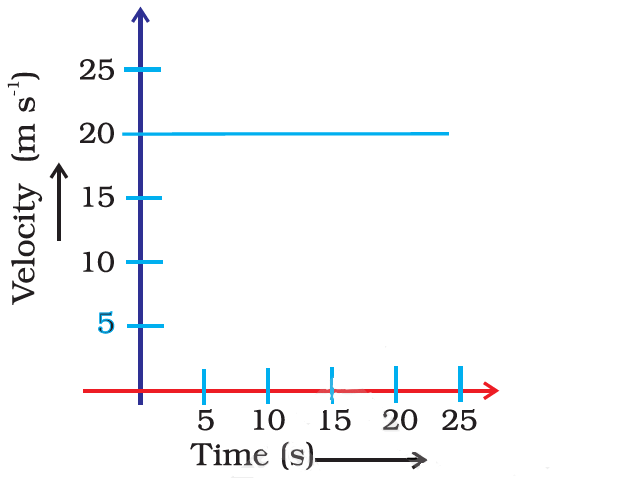
Ans: (i) As velocity is constant, acceleration is 0 ms-2
(ii) Here Velocity is constant hence, v = 20 m/s
(iii) s = v x t = 20 x 15 = 300 m
Q18. Draw a velocity versus time graph of a stone thrown vertically upwards and then coming downwards after attaining the maximum height.
Ans: Velocity versus time graph of a stone thrown vertically upwards and then coming downwards after attaining the maximum height as bellow:
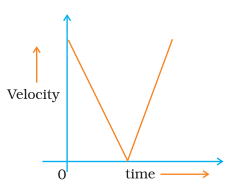
Long Answer Type Questions
Q19. An object is dropped from rest at a height of 150 m and simultaneously another object is dropped from rest at a height 100 m. What is the difference in their heights after 2 s if both the objects drop with the same acceleration? How does the difference in heights vary with time?
Ans:
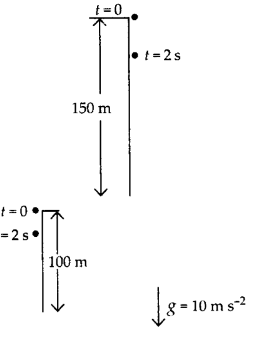
Initially difference between height of two objects = 150 - 100 = 50 m
Distance travelled by first object in 2s,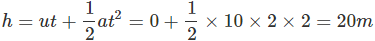
Distance travelled by second object in 2 seconds, 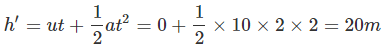
Height of first object (at t = 2s) = 150 - 20 = 130 m
Height of second object (at t = 2s) = 100 - 20 = 80 m
Difference in height (after t = 2s) = 130 - 80 = 50 m
Q20. An object starting from rest travels 20 m in first 2s and 160 m in next 4s. What will be the velocity after 7s from the start?
Ans: For first interval
u = 0, s = 20 m, t = 2 s
s = ut +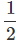 at2
at2
⇒ a = 2 s/t2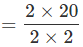 = 10 ms-2
= 10 ms-2
v = u + at = 10 x 2 = 20 ms-1
For second interval:
u = 20 ms-1, s = 160 m, t = 4 s
s = ut +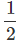 at2
at2
160 = 20 x 4 +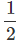 x a x 16a = 10 ms-2 (i.e. 'a' is constant)
x a x 16a = 10 ms-2 (i.e. 'a' is constant)
Velocity after 7 seconds:
v = u + at = 0 + 10 x 7 = 70 m/s
Q21. Using the following data, draw a time-displacement graph for a moving object: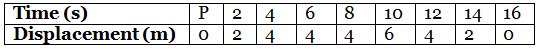 Use this graph to find average velocity for the first 4 s, for the next 4 s and for the last 6 s.
Use this graph to find average velocity for the first 4 s, for the next 4 s and for the last 6 s.
Ans:
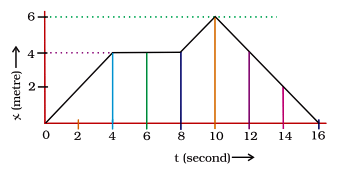 vavg for first 4s (i.e. Slope from t = 0s to t = 4s) =
vavg for first 4s (i.e. Slope from t = 0s to t = 4s) = 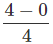 =1 m/s
=1 m/s
vavg (for t = 4 s to t = 8 s) = 0 (as slope is zero)
vavg (for t = 10 s to t = 16 s) = = - 1 m/s (i.e. the body is moving towards the origin)
= - 1 m/s (i.e. the body is moving towards the origin)
Q22. An electron moving with a velocity of 5 X 104 ms-1 enters into a uniform electric field and acquires a uniform acceleration of 104 ms-2 in the direction of its initial motion.
(a) Calculate the time in which the electron would acquire a velocity double of its initial velocity.
(b) How much distance the electron would cover in this time?
Ans: u = 5 x 104 m/s, a = 104 m/s2, v = 2u
(a) v = u + at
⇒ 2u = u + 104t,
⇒ t = u x 10-4 = 5 x 104 x 10-4 = 5 s.
(b) s = ut + 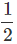 at2 = 5 x 104 x 5 +
at2 = 5 x 104 x 5 + 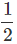 x 104 x (5)2 = 3.75 x 105 m
x 104 x (5)2 = 3.75 x 105 m
Q23. Obtain a relation for the distance travelled by an object moving with uniform acceleration in the interval between 4th and 5th seconds.
Ans: If u = initial velocity, then final velocity = 2m.
For acceleration a:
At t = 4s, s1 = ut + 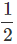 at2 = 4u + 8a
at2 = 4u + 8a
At t = 5s, s2 = ut + 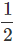 at2 = 5u +
at2 = 5u + 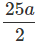
S2 - S1 = (5 - 4) u + 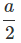 (25 - 16) = u +
(25 - 16) = u +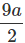
Q24. Two stones are thrown vertically upwards simultaneously with their initial velocities u1 and u2 respectively. Prove that the ratio of heights reached by them would be in the ratio of u12: u22 (Assume upward acceleration is -g and downward acceleration to be +g).
Ans: Given- velocities u1 and u2
heights h1 and h2
accelerations - g and g
At highest points, velocities v1 = v2 = 0
Thus, v2 = u2 + 2as
⇒ v12 = u12 - 2gh1 and v22 = u22 - 2gh2
⇒ 0 = u12 - 2gh1 and 0 = u22 - 2gh2
⇒ u12 = 2gh1 and u22 = 2gh2
Therefore,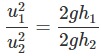 i.e. u12 : u22 = h1 : h2
i.e. u12 : u22 = h1 : h2
|
84 videos|478 docs|60 tests
|
FAQs on NCERT Exemplar: Motion - Science Class 9
| 1. What is the definition of motion in physics? |  |
| 2. What are the different types of motion? |  |
| 3. How do you calculate speed and velocity? |  |
| 4. What is the difference between distance and displacement? |  |
| 5. What is uniform motion and non-uniform motion? |  |

















