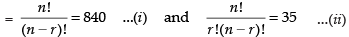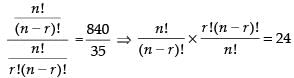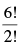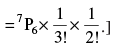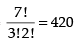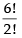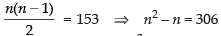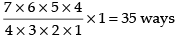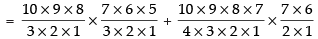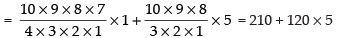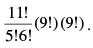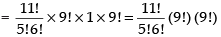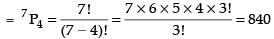Fill in the Blanks
Q.41. If nPr = 840, nCr = 35, then r = ______.
Ans.
Given that nPr = 840 and nCr = 35
⇒ 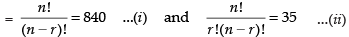
Dividing eq. (i) by eq. (ii) we get
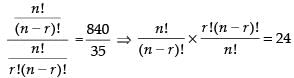
⇒ r! = 24 ⇒ r! = 4 x 3 x 2 x 1
⇒ r! = 4! ∴ r = 4
Hence the value of the filler is 4.
Q.42. 15C8 + 15C9 – 15C6 – 15C7 = ______.
Ans.
15C8 + 15C9 – 15C6 – 15C7 = 15C15 – 8 + 15C15 – 9 – 15C6 – 15C7
[∴ nCr = nCn – r]
= 15C7 + 15C6 – 15C6 – 15C7 = 0
Hence, the value of the filler is 0.
Q.43. The number of permutations of n different objects, taken r at a line, when repetitions are allowed, is ______.
Ans.
Number of permutation of n different objects, taken r at a time is nr.
Q.44. The number of different words that can be formed from the letters of the word INTERMEDIATE such that two vowels never come together is ______. [Hint: Number of ways of arranging 6 consonants of which two are alike is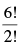
and number of ways of arranging vowels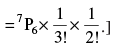
Ans.
Total number of words is INTERMEDIATE = 12
which have 6 vowels and 6 consonants
If two vowels never come together then we can arrange as under
V C V C V C V C V C V C V
Here, vowels are IEEIAE where 2 I’s and 3 E’s are there.
∴ Number of ways of arranging vowels =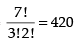
Consonants are NTRMDT where 2T’s are there
∴ Number of ways arranging consonants =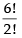

So, the total number of words are
= 420 x 360 = 151200
Hence, the value of the filler is 151200.
Q.45. Three balls are drawn from a bag containing 5 red, 4 white and 3 black balls. The number of ways in which this can be done if at least 2 are red is ______.
Ans.
We have 5 red, 4 white and 3 black balls out of which atleast 2 red balls are to be drawn
∴ Number of ways = 5C2 x 7C1 + 5C3
= 10 x 7 + 10 = 70 + 10 = 80
Hence, the value of the filler = 80.
Q.46. The number of six-digit numbers, all digits of which are odd is ______.
Ans.
Out of the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 the odd digits are 1, 3, 5, 7, 9.
Therefore number of 6 digit numbers = (5)6
Hence, the value of the filler is (5)6.
Q.47. In a football championship, 153 matches were played . Every two teams played one match with each other. The number of teams, participating in the championship is ______.
Ans.
Let the number of participating teams be n
Given that every two teams played one match with each other.
∴ Total number of matches played = nC2
So nC2 = 153
⇒ 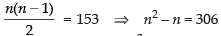
⇒ n2 – n – 306 = 0 ⇒ n2 – 18n + 17n – 306 = 0
⇒ n(n – 18) + 17 (n – 18) = 0 ⇒ (n - 18) (n + 17) = 0
⇒ n – 18 = 0 and n + 17 = 0
⇒ n = 18, n ≠ - 17
Hence, the value of the filler is 18.
Q.48. The total number of ways in which six ‘+’ and four ‘–’ signs can be arranged in a line such that no two signs ‘–’ occur together is ______.
Ans.
The following may be the arrangement of (–) and (+)
(–) (+) (–) (+) (–) (+) (–) (+) (–) (+) (–) (+) (–)
Therefore, ‘+’ sign can be arranged only is 1 way because all are identical.
and 4(–) signs can be arranged at 7 places in 7C4 ways
∴ Total number of ways = 7C4 x 1 =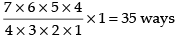
Hence, the value of the filler is 35.
Q.49. A committee of 6 is to be chosen from 10 men and 7 women so as to contain atleast 3 men and 2 women. In how many different ways can this be done if two particular women refuse to serve on the same committee.
[Hint:At least 3 men and 2 women: The number of ways = 10C3 × 7C3 + 10C4 × 7C2. For 2 particular women to be always there: the number of ways = 10C4 + 10C3 × 5C1 . The total number of committees when two particular women are never together = Total – together.]
Ans.
We have 10 men and 7 women out of which a committee of 6 is to be formed which contain atleast 3 men and 2 women
Therefore, Number of ways = 10C3 x 7C3 + 10C4 x 7C2
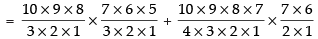
= 120 x 35 + 210 x 21 = 4200 + 4410 = 8610
If 2 particular women to be always present, then the number
of ways = 10C4 x 5C0 + 10C3 x 5C1
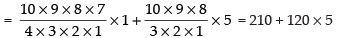
= 210 + 600 = 810
∴ Total number of committee = 8610 - 810 = 7800
Hence, the value of the filler is 7800.
Q.50. A box contains 2 white balls, 3 black balls and 4 red balls. The number of ways three balls be drawn from the box if at least one black ball is to be included in the draw is ______.
Ans.
We have 2 white, 3 black and 4 red balls It is given that atleast 1 black ball is to be included.
∴ Required number of ways = 3C1 x 6C2 + 3C2 x 6C1 + 3C3
= 3 x 15 + 3 x 6 + 1 = 45 + 18 + 1 = 64
Hence, the value of the filler is 64.
TRUE/FALSE STATEMENT
Q.51. There are 12 points in a plane of which 5 points are collinear, then the number of lines obtained by joining these points in pairs is 12C2 – 5C2.
Ans.
Required number of lines = 12C2 – 5C2 + 1
Hence, the given statement is ‘False’
Q.52. Three letters can be posted in five letterboxes in 35 ways.
Ans.
Given that 3 letters are to be posted in 5 letter boxes
∴ Required number of ways = 53 = 125
Hence, the given statement is ‘False’
Q.53. In the permutations of n things, r taken together, the number of permutations in which m particular things occur together is n–mPr–m × rPm.
Ans.
Arrangement of n things, r taken at a time in which m things occur together.
So, number of object excluding m object = (r – m)
Here, we first arrange (r – m + 1) object
∴ Number of arrangements = (r - m + 1)!
m objects can be arranged in m! ways
So, the required number of arrangements = (r - m + 1)! x m!
Hence, the given statement is ‘False’.
Q.54. In a steamer there are stalls for 12 animals, and there are horses, cows and calves (not less than 12 each) ready to be shipped. They can be loaded in 312 ways.
Ans.
There are 3 types of animals horses, cows and calves not less than 12 each.
So, number of ways of loading = 312
Hence, the given statement is ’True‘.
Q.55. If some or all of n objects are taken at a time, the number of combinations is 2n–1.
Ans.
When some or all objects, taken at a time, then the number of selection will be
nC1 + nC2 + nC3 + … + nCn = 2n –1
[∴ nC0 + nC1 + nC2 + … + nCn = 2n]
Hence, the given statement is ‘True’.
Q.56. There will be only 24 selections containing at least one red ball out of a bag containing 4 red and 5 black balls. It is being given that the balls of the same colour are identical.
Ans.
We have 4 red and 5 black balls in a box and atleast one red ball is to be drawn
∴ Number of selection = [(4 + 1) (5 + 1) - 1] - 5 = [5 x 6 - 1] - 5
29 - 5 = 24
Hence, the given statement is ‘True’.
Q.57. Eighteen guests are to be seated, half on each side of a long table. Four particular guests desire to sit on one particular side and three others on other side of the table. The number of ways in which the seating arrangements can be made is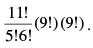
[Hint: After sending 4 on one side and 3 on the other side, we have to select out of 11; 5 on one side and 6 on the other. Now there are 9 on each side of the long table and each can be arranged in 9! ways.]
Ans.
When 4 guests sit can one side and 3 on the other side, we have to select out of 11. 5 sit one one side and 6 sit on the other side.
Now, remaining selecting on one half side = 18 – 4 – 3C5 = 11C5
and the other half side = (11 – 5)C6 = 6C6
So, the total arrangements = 11C5 x 9! x 6C6 x 9!
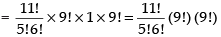
Hence, the given statement is ’True‘.
Q.58. A candidate is required to answer 7 questions out of 12 questions which are divided into two groups, each containing 6 questions. He is not permitted to attempt more than 5 questions from either group. He can choose the seven questions in 650 ways.
Ans.
The candidate may attempt in following manner

So, the number of attempts of 7 questions
= 6C2 x 6C5 + 6C3 x 6C4 + 6C4 x 6C3 + 6C5 x 6C2
= 2[6C2 x 6C5 + 6C3 x 6C4]
= 2 [15 x 6 + 20 x 15] = 2[90 + 300] = 2 x 390 = 780.
Q.59. To fill 12 vacancies there are 25 candidates of which 5 are from scheduled castes. If 3 of the vacancies are reserved for scheduled caste candidates while the rest are open to all, the number of ways in which the selection can be made is 5C3 × 20C9.
Ans.
Number of ways to select 3 scheduled caste candidate out of 5 = 5C3
We have to select 9 other candidates out of 22.
So the number of ways = 22C9
Required number of selection = 5C3 x 22C9
Hence, the given statement is False.
MATCH THE COLUMNS
Q.60. There are 3 books on Mathematics, 4 on Physics and 5 on English. How many different collections can be made such that each collection consists of :

Ans.
We have 3 books of Mathematics, 4 of Physics and 5 on English
(a) One book of each subject = 3C1 x 4C1 x 5C1 = 3 x 4 x 5 = 60
(b) Atleast one book of each subject = (23 - 1) x (24 - 1) x (25 - 1)
= 7 x 15 x 31 = 3255
(c) Atleast one book of English = (25 – 1) x 27 = 31 x 128 = 3968.
Hence the required matching is
(a) ↔ (ii), (b) ↔ (iii) and (c) ↔ (i)
Q.61. Five boys and five girls form a line. Find the number of ways of making the seating arrangement under the following condition:

Ans.
(a) Total number of arrangement when boys and girls alternate: = (5!)2 + (5!)2
(b) No two girls sit together: = 5! 6!
(c) All the girls sit together = 2! 5! 5!
(d) All the girls sit never together = 10! – 5! 6!
Hence, the required matching is
(a) ↔ (iii), (b) ↔ (i), (c) ↔ (iv), (d) ↔ (ii)
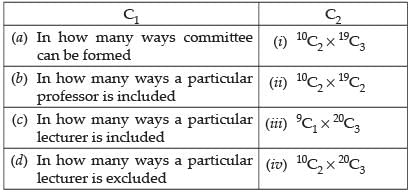
Q.62. There are 10 professors and 20 lecturers out of whom a committee of 2 professors and 3 lecturer is to be formed. Find :
Ans.
(a) We have to select 2 professor out of 10 and 3 lecturers out of 20
∴ Number of ways of selection = 10C2 x 20C3
(b) When a particular professor is included taken the number of ways = 10-1C1 x 20C3 = 9C1 x 20C3
(c) When a particular lecturer is included then number of ways = 10C2 x 19C2
(d) When a particular lecturer is excluded, then number of ways = 10C2 x 19C3
Hence the required matching is
(a) ↔ (iv), (b) ↔ (iii), (c) ↔ (ii), (d) ↔ (i)
Q.63. Using the digits 1, 2, 3, 4, 5, 6, 7, a number of 4 different digits is formed. Find

Ans.
(a) Total of 4 digit number formed with 1, 2, 3, 4, 5, 6, 7
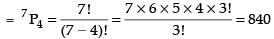
(b) When a number is divisible by 2 = 4 x 5 x 6 x 3 = 360
(c) Total numbers which are divisible by 25 = 40
(d) Total numbers which are divisible by 4 (last two digits is divisible by 4) = 200
Hence, the required matching is
(a) ↔ (i), (b) ↔ (iii), (c) ↔ (iv), (d) ↔ (ii)
Q.64. How many words (with or without dictionary meaning) can be made from the letters of the word MONDAY, assuming that no letter is repeated, if

Ans.
(a) 4 letters are used at a time =
(b) All letters are used at a time = 6P6 = 6! = 720
(c) All letters are used but first letter is vowel = 2 x 5! = 2 x 120 = 240
Hence, the required matching is
(a) ↔ (iii), (b) ↔ (i), (c) ↔ (ii)