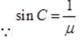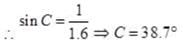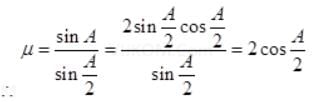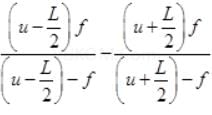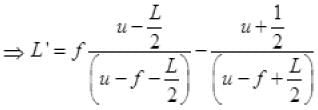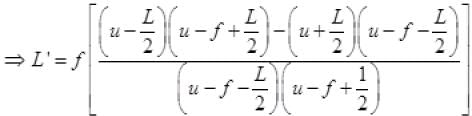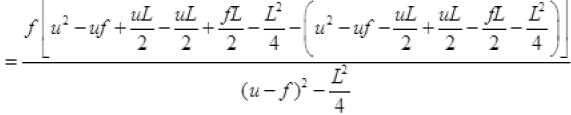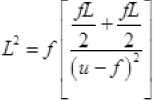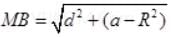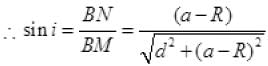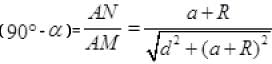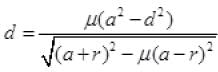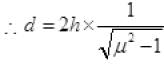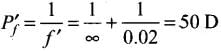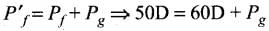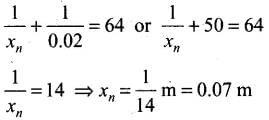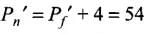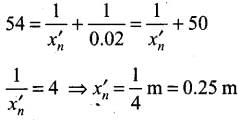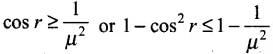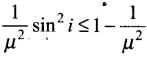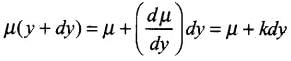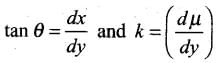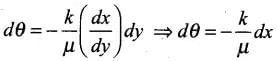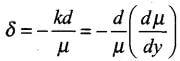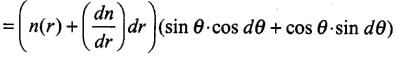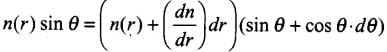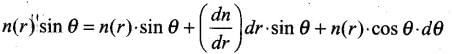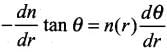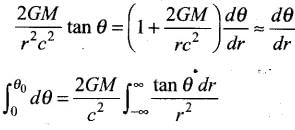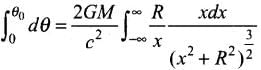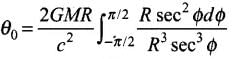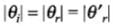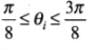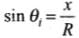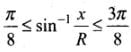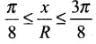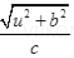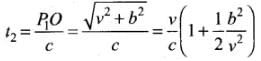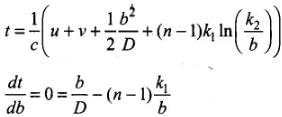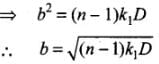NCERT Exemplar: Ray Optics & Optical Instruments | Physics Class 12 - NEET PDF Download
| Table of contents |

|
| Multiple-Choice Questions |

|
| Very Short Answer Type Questions |

|
| Short Answer Type Questions |

|
| Long Answer Type Questions |

|
Multiple-Choice Questions
Q.1. A ray of light incident at an angle θ on a refracting face of a prism emerges from the other face normally. If the angle of the prism is 5° and the prism is made of a material of refractive index 1.5, the angle of incidence is
(a) 7.5°.
(b) 5°.
(c) 15°.
(d) 2.5°.
Correct Answer is Option (a)
A = 5°
μ = 1.5
i2 = 0°
r2=0°
r1 + r2 = A
r1= A − r2 = 5 − 0 = 5°
μ = sini1/sinr1
⇒ sini1 = μ sin r1
= 1.5 x sin 5°
= 1.5 x 0.087
= 0.1305
= 7.5 °
Q.2. A short pulse of white light is incident from air to a glass slab at normal incidence. After travelling through the slab, the first colour to emerge is
(a) Blue.
(b) Green.
(c) Violet.
(d) Red.
Correct Answer is Option (d)
As velocity of wave is given by the relation v = f λ. When light ray goes from one medium to other medium, the frequency of light remains unchanged. Hence v ∝ λ or greater the wavelength, greater the speed.
The light of red colour is of highest wavelength and therefore of highest speed. Therefore, after travelling through the slab, the red colour emerges first.
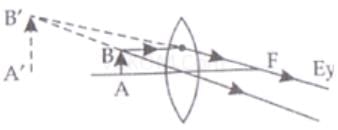
Q.3. An object approaches a convergent lens from the left of the lens with a uniform speed 5 m/s and stops at the focus. The image
(a) Moves away from the lens with a uniform speed 5 m/s.
(b) Moves away from the lens with uniform acceleration.
(c) Moves away from the lens with a non-uniform acceleration.
(d) Moves towards the lens with a non-uniform acceleration.
Correct Answer is Option (c)
In our problem the object approaches a convergent lens from the left of the lens with a uniform speed of 5 m/s, hence the image will move away from the lens with a non-uniform acceleration, the image moves slower in the beginning and faster later on will move from F to 2F and when the object moves from 2F to F, the image will move from 2F to infinity. At 2F, the speed of the object and image will be equal.
Q.4. A passenger in an aeroplane shall
(a) Never see a rainbow.
(b) May see a primary and a secondary rainbow as concentric circles.
(c) May see a primary and a secondary rainbow as concentric arcs.
(d) Shall never see a secondary rainbow.
Correct Answer is Option (b)
As aeroplane is at higher altitude, the passenger in an aeroplane may see a primary and a secondary rainbow like concentric circles.
• If an object move with constant speed (V0) towards a convex lens from infinity to focus, the image will move slower in the beginning and then faster. Also
Vi = (f / f + u)2 . V0
If an object approaches the lens, the image moves away from lens with a non-uniform acceleration.
Q.5. You are given four sources of light each one providing a light of a single colour – red, blue, green and yellow. Suppose the angle of refraction for a beam of yellow light corresponding to a particular angle of incidence at the interface of two media is 90°. Which of the following statements is correct if the source of yellow light is replaced with that of other lights without changing the angle of incidence?
(a) The beam of red light would undergo total internal reflection.
(b) The beam of red light would bend towards normal while it gets refracted through the second medium.
(c) The beam of blue light would undergo total internal reflection.
(d) The beam of green light would bend away from the normal as it gets refracted through the second medium.
Correct Answer is Option (c)
We know that if angle of refraction is 90° for the length then incidence angle is called critical angle. So light rays are passing from denser to rarer medium.
As sin c = 1 / μ so, c ∝ 1 / μ > μv > μg > μy > μR
So, critical angle for Cv < Cg< CY < CR, i.e., critical angle of blue and green light is smaller than that of yellow and it is greater for red colour light.
As the angle of refraction for yellow light is 90° for a particular incident angle. This incidence angle is critical angle for yellow let it be CY. As CR>Cv. So it will not get total internal reflection and CV < CY,Cg < CY.
So light of blue and green colour get total internal reflection. So correct answer is (c).
Q.6. The radius of curvature of the curved surface of a plano-convex lens is 20 cm. If the refractive index of the material of the lens be 1.5, it will
(a) Act as a convex lens only for the objects that lie on its curved side.
(b) Act as a concave lens for the objects that lie on its curved side.
(c) Act as a convex lens irrespective of the side on which the object lies.
(d) Act as a concave lens irrespective of side on which the object lies.
Correct Answer is Option (c)
If object lies on curved side then R1 = +20 cm and R2 = ∞, μ1 =1, μ2=1.5
1 / f = (μ2 - μ1)(1 / R1 - 1 / R2)
1 / f = (1.5 - 1)(1 / 20 - 1 / ∞) = 0.5 / 20 = 5 / 200 = 1 / 40F=+ 40cm
If object lies on plane side R1= and ∞ R2= -20 cm, μ1= 1, μ2= 1.5
1 / f = (μ2 - μ1)(1 / R1 - 1 / R2)
1 / f = (1.5 - 1)(1 / ∞ - (-1 / 20))] = 0.5 x (+1 / 20)
1 / f = 5 / 200
f= +40 cm
So, lens will always act as a convex lens irrespective of side on which objects lie.
Q.7. The phenomena involved in the reflection of radio waves by the ionosphere is similar to
(a) Reflection of light by a plane mirror.
(b) Total internal reflection of light in the air during a mirage.
(c) Dispersion of light by water molecules during the formation of a rainbow.
(d) Scattering of light by the particles of air.
Correct Answer is Option (b)
Ionosphere is a transparent optical medium and radio wave is reflected back. Reflection through transparent surface is total internal reflection so that internal reflection of radio wave takes place.
Q.8. The direction of ray of light incident on a concave mirror is shown by PQ while directions in which the ray would travel after reflection is shown by four rays marked 1, 2, 3 and 4 (Fig.). Which of the four rays correctly shows the direction of reflected ray?
(a) 1
(b) 2
(c) 3
(d) 4
Correct Answer is Option (b)
The ray PQ of light passes through focus F and incident on the concave mirror, after reflection, should become parallel to the principal axis and shown by ray 2 in the figure.
Important points:
We can locate the image of any extended object graphically by drawing any two of the following four special rays:
1. A ray initially parallel to the principal axis is reflected through the focus of the mirror (1).
2. A ray passing through the center of curvature is reflected back along itself (3).
3. A ray initially passing through the focus is reflected parallel to the principal axis (2).
4. A ray incident at the pole is reflected symmetrically.
Q.9. The optical density of turpentine is higher than that of water while its mass density is lower. Fig. shows a layer of turpentine floating over water in a container. For which one of the four rays incident on turpentine in Fig, the path shown is correct?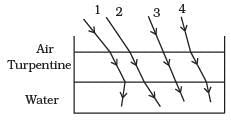 (a) 1
(a) 1
(b) 2
(c) 3
(d) 4
Correct Answer is Option (b)
μa < μT > μw. Here, incidence ray passes from air to turpentine to water, i.e., from rare to denser then denser to rarer so first it bends towards normal then away from normal so the path shown is correct for ray (2).
Q.10. A car is moving with at a constant speed of 60 km h–1 on a straight road. Looking at the rear view mirror, the driver finds that the car following him is at a distance of 100 m and is approaching with a speed of 5 km h–1. In order to keep track of the car in the rear, the driver begins to glance alternatively at the rear and side mirror of his car after every 2 s till the other car overtakes. If the two cars were maintaining their speeds, which of the following statement (s) is/are correct?
(a) The speed of the car in the rear is 65 km h–1.
(b) In the side mirror the car in the rear would appear to approach with a speed of 5 km h-1 to the driver of the leading car.
(c) In the rear view mirror the speed of the approaching car would appear to decrease as the distance between the cars decreases.
(d) In the side mirror, the speed of the approaching car would appear to increase as the distance between the cars decreases.
Correct Answer is Option (d)
• Object placed in front of mirror: For all position of object in front of a mirror, image is virtual, erect and smaller in size.
• As object moves towards the pole, magnification increases and tends to unity at pole.
• Object moving along the principal axis: On differentiating the mirror formula with respect to time, we get dv / dt = -(v / u)2 = du / dt = -(f / u - f)2 . du / dt where dv / dt is the velocity of image along the principal axis and du/dt is the velocity of object along the principal axis. Negative sign implies that the image, in case of mirror, always moves in the direction opposite to that of the object.
As the distance between the cars decreases, the speed of the image of the car would appear to increase.
Q.11. There are certain material developed in laboratories which have a negative refractive index (Fig.). A ray incident from air (medium 1) into such a medium (medium 2) shall follow a path given by
(a) 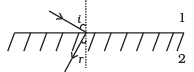
(b) 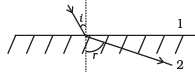
(c) 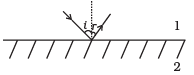
(d) 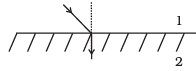
Correct Answer is Option (a)
The materials with negative refractive index responds to Snell’s law just opposite way. If incident ray from air (Medium 1) incident on those material, the ray refract or bend same side of the normal as in option (a).
Q.12. Consider an extended object immersed in water contained in a plane trough. When seen from close to the edge of the trough the object looks distorted because
(a) The apparent depth of the points close to the edge are nearer the surface of the water compared to the points away from the edge.
(b) The angle subtended by the image of the object at the eye is smaller than the actual angle subtended by the object in air.
(c) Some of the points of the object far away from the edge may not be visible because of total internal reflection.
(d) Water in a trough acts as a lens and magnifies the object.
Correct Answer is Option (a), (b) & (c)
- We know that shifting (h) of the image of an object immersed in liquid from an object is directly proportional to the real distance of the object from the surface of liquid
t=real depth or distance of the object from the surface of the liquid of refractive index μ: If the object is seen from one edge of the trough the relative differences of depth (distance) in H2O between two ends of objects is larger than if it seen from the top or away from the edge. By above formula or distortion of the nearer end is smaller than farther, verifies the option (a).
- The angle subtended by an object is larger than its image in the water, as its image shifts upward verify option (b).
- Rays coming out from object to observer passes from denser to rarer medium, and angle of incidence for rays from farther end B of the object is larger than near end A. The incidence angles for rays coming from end 3 may have incidence angle more than the critical angle and can cause total internal reflection, so will not reach to the observer, cause non-visible of farther end verifies option (c).
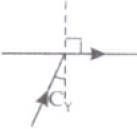
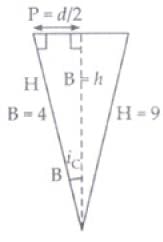
Q.13. A rectangular block of glass ABCD has a refractive index 1.6. A pin is placed midway on the face AB (Fig.). When observed from the face AD, the pin shall

(a) Appear to be near A.
(b) Appear to be near D.
(c) Appear to be at the centre of AD.
(d) Not be seen at all.
Correct Answer is Option (a) & (b)
A point P is on the mid point of face AB. When seen through face AD, near to point A, the angle of incidence (i1) will be smaller than critical angle ic = 38.7o So image of P will at P’ and image can be seen at P’. P’ is nearer to both A and D as compared to P verifies option (a) and (b). When seen near point D through face AD, angle of incidence i2 > ic. so total internal reflection takes place and object cannot be observed. But object can be seen when viewed near to A so option (d) not verified.
Q.14. Between the primary and secondary rainbows, there is a dark band known as Alexander's dark band. This is because
(a) Light scattered into this region interfere destructively.
(b) There is no light scattered into this region.
(c) Light is absorbed in this region.
(d) Angle made at the eye by the scattered rays with respect to the incident light of the sun lies between approximately 42° and 50°.
Correct Answer is Option (a) & (d)
The Alexander's dark band lies between the primary and secondary rainbows, formed due to light scattered into this region interfere destructively. The primary rainbows subtends an angle nearly 41° to 42° at observer’s eye, whereas secondary rainbows subtends an angle nearly 51° to 54° at observer’s eye w.r.t. incident light ray.
Hence, the scattered rays with respect to the incident light of the sun lies between approximately 42° and 50°.
Q.15. A magnifying glass is used, as the object to be viewed can be brought closer to the eye than the normal near point. This results in
(a) A larger angle to be subtended by the object at the eye and hence viewed in greater detail.
(b) The formation of a virtual erect image.
(c) Increase in the field of view.
(d) Infinite magnification at the near point.
Correct Answer is Option (a) & (b)
In the magnifying glass, the object is placed within the focal length and the image formed is magnified and erect. As (A’B’) image is magnified so it subtends larger angle at the eye than the object (AB), so can be seen more clearly.
Q.16. An astronomical refractive telescope has an objective of focal length 20m and an eyepiece of focal length 2cm.
(a) The length of the telescope tube is 20.02m.
(b) The magnification is 1000.
(c) The image formed is inverted.
(d) An objective of a larger aperture will increase the brightness and reduce chromatic aberration of the image.
Correct Answer is Option (a), (b) & (c)
The length of the telescope
L = fo + fe = 20 + 00.02 = 20.02 m
and m = fo / fe = 20m / 0.02m = 2000 / 2 = 1000
The final image formed in telescope (Refracting) is inverted, virtual and smaller than object.
Very Short Answer Type Questions
Q.17. Will the focal length of a lens for red light be more, same or less than that for blue light?
The refractive index depends on colour of light or wavelength of light.
Cauchy's equation: μ = A + B / λ2 + C / λ4 + ...
As λred > λblue hence μred < μblue
Hence parallel beams of light incident on a lens will be bent more towards the axis for blue light compared to red.
By lens marker's formula,
1 / f = (μ - 1)(1 / R1 - 1 / R2)
The refractive index for red light is less than that for blue light μred < μblue
Hence 1 / fred < 1 / fblue ⇒ fred > fblue
Thus, the focal length for red light will be greater than that for blue light.
Q.18. The near vision of an average person is 25cm. To view an object with an angular magnification of 10, what should be the power of the microscope?
It is given, the least distance of distinct vision of an average person (i.e., D) is 25 cm, in order to view an object with magnification 10,
Here, v = D = 25 cm and u = f
But the magnification m = v / u = D / f
⇒ f = D / m = 25 / 10 = 2.5 cm = 0.025 m
But power P = 1 / f(in m) = 1 / 0.025 = 40D
This is the required power of lens.
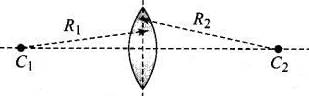
Q.19. An unsymmetrical double convex thin lens forms the image of a point object on its axis. Will the position of the image change if the lens is reversed?
Thin lens formula: 1/v - 1/u = 1/f
For a given object position if focal length of the lens does not change, the image position remains unchanged.
By lens maker's formula,
1 / f = (μ - 1)(1 / R1 - 1 / R2)For this position R1 is positive and R2 is negative. Hence focal length at this position
1 / f1 = (μ - 1)(1 / (+R1) - 1 / (-R2) = (μ - 1)(1 / R1 + 1 / R2)
Now the lens is reversed,
At this position, R2 is positive and R1 is negative. Hence focal length at this position is
1 / f2 = (μ - 1)(1 / (+R2) - 1 / (-R1) = (μ - 1)(1 / R1 + 1 / R2)
We can observe the focal length of the lens does not change in both positions, hence the image position remains unchanged.
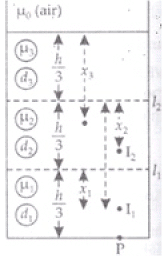
Q.20. Three immiscible liquids of densities d1 > d2 > d3 and refractive indices µ1 > µ2 > µ3 are put in a beaker. The height of each liquid column is h/3. A dot is made at the bottom of the beaker. For near normal vision, find the apparent depth of the dot.
The liquids are immiscible, so liquids arranged from bottom to top d1, d2 and d3 with their refractive indices μ1, μ2, μ3 respectively separated by layers l1, l2 as shown in figure.
Consider the layer l1. Let object is at its bottom at P then distance (x1) of image of P by liquid of refractive index μ1 from layer l1
x1 = h / 3 / 2μ1 ∴ 2μ1 = μ1 / μ2
x1 = h / 3μ1 / μ2 = h / 3 . μ2 / μ1
This image I1 acts as object for liquid of μ2 and form the image at I2.
The distance x2 below level l2
Real depth = (h/2 +x1)
x2 = Real depth / 3μ2 = Real depth / μ2 / μ3
x2 = μ3 / μ2[h / 3 + x1] = μ3 / μ2[h / 3 + h / 3 . μ2 / μ1] = h / 3 . μ3 / μ2[1 + μ2 / μ1
= h / 3 [μ3 / μ2 + μ3 / μ2 . μ2 / μ1] = h / 3[μ3 / μ2 + μ3 / μ1]
As the point P is seen from outside
x3 = μ0 / μ3[h / 3 + x2] = 1 / μ3[h / 3 + h / 3(μ3 / μ2 + μ3 / μ1)]
[∵ μ0 = 1 refractive index of air]
= h / 3[1 / μ3 + 1 / μ3(μ3 / μ2 + μ3 / μ1)]
x3 = h / 3[1 / μ3 + μ3 / μ3(1 / μ2 + 1 / μ1)] = h / 3[1 / μ3 + 1 / μ2 + 1 / μ1]
X3 is apparent depth.
Q.21. For a glass prism (µ = √3) the angle of minimum deviation is equal to the angle of the prism. Find the angle of the prism.
The required relation for minimum angle of deviation
[∵ δm = A (given)]
√3 = 2 cos A / 2 ⇒ cos A / 2 = √3 / 2
cos A / 2 = cos 30° ⇒ A / 2 = 30°
A = 60° is angle of prism.
Short Answer Type Questions
Q.22. A short object of length L is placed along the principal axis of a concave mirror away from focus. The object distance is u. If the mirror has a focal length f, what will be the length of the image? You may take L <<|v - f|.
As the mean distance of object from mirror is u
∴ u1 = u - L / 2 and u2 = (u + L / 2)
Let the image of the two ends of object form at distance v1 and v2 (v1 > v2). So length of image on principal axis is L’ = (v1 - v2)
1 / v + 1 / u = 1 / f or 1 / v + 1 / f = 1 / u
⇒ 1 / v = u - f / uf ⇒ v = uf / u - f
So L’ = v1 - v2 =
∴ L<<(u - f) ∴ L2/4 <<<(u - f)
So neglecting the terms L2/4
L' = f fL / (u - f)2 ⇒ L' = Lf2 / (u - f)2
It is the length of image f.
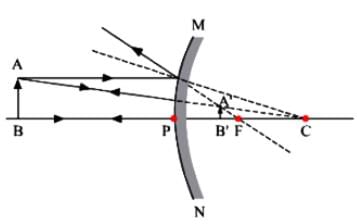
Q.23. A circular disc of radius ‘R ’ is placed co-axially and horizontally inside an opaque hemispherical bowl of radius ‘a’ (Fig.). The far edge of the disc is just visible when viewed from the edge of the bowl. The bowl is filled with transparent liquid of refractive index µ and the near edge of the disc becomes just visible. How far below the top of the bowl is the disc placed?
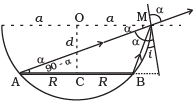
In figure AM and BM are the rays from the ends of disc AB reaching at one end of bowl at M.MN is tangent at M, so MN ⊥ AB i.e., ∠N = 90°
Taking incidence ray BM and refracted ray MD
BN = CN - CB = OM - CB = a - R
∠r = ∠α =∠AMN
Sin r = cos
For incidence ray BM to the horizontal level of liquid MP, MN will be normal at M. ∠i and ∠r will be incidence and refracted angles when ray BM passes from liquid (μ) to air. By Snell’s law, as ray passes from liquid to air
1μ0 = sin i / sin r ⇒ μ0 / μ1 = sin i / sin r [μ0 for air = 1] [μ1 = μ for liquid]
1 / μ1 = sin i / sin r
It is required expression.
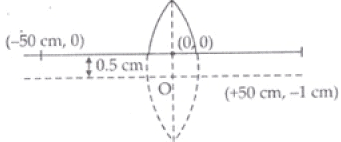
Q.24. A thin convex lens of focal length 25 cm is cut into two pieces 0.5 cm above the principal axis. The top part is placed at (0, 0) and an object placed at (-50 cm, 0). Find the coordinates of the image.
Object is placed 0.5 cm above principal axis
u = -50cm f = +25cm, v = ?
1 / v - 1 / u = 1 / f
1 / v - 1 / -50 = 1 / 25
1 / v = 1 / 25 - 1 / 50
= 2 - 1 / 50 = 1 / 50
v = 50 cm
m = +v / u = +(50) / -50 = -1
So the size of image is equal to that of object, m is negative so image is inverted.
So image is at (50cm, -1cm) and 0.5 cm below the X – X’ axis.
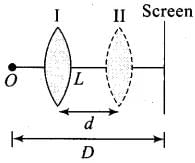
Q.25. In many experimental set-ups the source and screen are fixed at a distance say D and the lens is movable. Show that there are two positions for the lens for which an image is formed on the screen.
Find the distance between these points and the ratio of the image sizes for these two points.
This is also one of the methods for finding focal length of the length in laboratory and knows as “Displacement method”.
1 / f = 1 / v - 1 / u
Consider a convex lens L placed between an object O and a screen S. The distance between the object and the screen is D and the positions of the object and the screen are held fixed. The lens can be moved along the axis of the system and at a position I a sharp image will be formed on the screen. Interestingly, there is another position on the same axis where a sharp image will once again be obtained on the screen. The position is marked as II in Figure.
In the figure, let the distance of position I from the object be x1. Then the distance of the screen from the lens is D-x1.
Therefore, u = x1 and v = +(D - x1).
Placing it in the lens formula,
1 / D - x1 - 1 / (-x1) = 1 / f ...(i)
At position II, let the distance of the lens from the screen be x2. Then the distance of the screen from the lens is D-x2.
Therefore, u = -x2 and v = +(D-x2).
Placing it in the lens formula1 / D - x2 - 1 / (-x2) = 1 / f ...(ii)
Comparing Eqs. (i) and (ii), we realize that there are only two solutions:
1. x1 = x2; or
2. D - x1 = x2 and D - x2 = x1
The first solution is trivial. Therefore, if the first position of the lens, for a sharp image, is x1 from the object, the second position is at D - x1 from the object.
Let the distance between the two positions I and II be d.
From the diagram, it is clear that
D = x1 + x2 and d = x2 - x1 ...(iii)
On solving, two equations in (iii) we have
x1 = D - d / 2 and D - x2 = D + d / 2 ...(iv)
Substituting Eq. (iv) in Eq. (i), we get...(v)
or...(vi)
If u = D / 2 + d / 2, then the image is at v = D / 2 - d / 2.
∴ The magnification m1 = D - d / D + d
If u = D - d / 2, then v = D + d / 2
∴ The magnification m2 = D + d / D - d
Thus, m2 / m1 = (D + d / D - d)2
This is the required expression of magnification.
Important Points:
• We notice from Eq. (vi) that a solution for d is possible only when D ≥ 4f.
• When D < 4f, there is no position for which a sharp image can be formed.
• When D = 4f, there is only one position where a sharp image is formed.
• When D > 4f, there are two positions where a sharp image is formed.
• The method is suitable for convex lenses only.
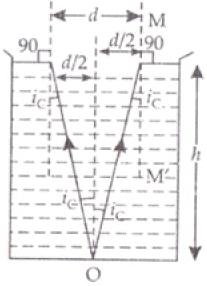
Q.26. A jar of height h is filled with a transparent liquid of refractive index µ (Fig.). At the centre of the jar on the bottom surface is a dot. Find the minimum diameter of a disc, such that when placed on the top surface symmetrically about the centre, the dot is invisible.
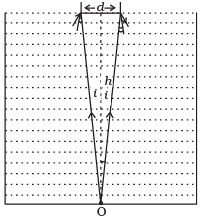
The point O will be invisible if the light ray coming from O does not come out or it get graze the surface of liquid or gets total internal reflection as in figure here.
Ray OA is incident at A with critical angle iC and it’s angle of refraction will be 90°.
For other ray if incident angle is more than ic it will get total internal reflection from the surface so will not come out from liquid.
So disc of diameter d is required to stop the rays from ‘O’ out of liquid.
B2 = H2 - P2
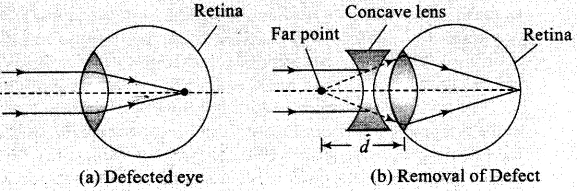
Q.27. A myopic adult has a far point at 0.1 m. His power of accommodation is 4 diopters.
(i) What power lenses are required to see distant objects?
(ii) What is his near point without glasses?
(iii) What is his near point with glasses? (Take the image distance from the lens of the eye to the retina to be 2 cm.)
1 / f = 1 / f1 + 1 / f2
in terms of power P = P1 + P2
(i) If for the normal relaxed eye of an average person, the power at the far point be Pf. The required power
Pf = 1 / f = 1 / 0.1 + 1 / 0.02 = 60 D
By the corrective lens the object distance at the far point is ∞.
The power required is,
Now for eye + lens system, we have the sum of the eye and that of the glasses Pg
which gives, Pg = -10D
(ii) For the normal eye his power of accommodation is 4D. Let the power of the normal eye for near vision be Pn.
Then, 4 = Pn - Pf or Pn = 64D
Let his near point be xn, then
(iii) With glasses
Long Answer Type Questions
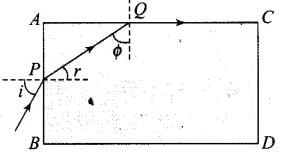
Q.28. Show that for material with refractive index µ ≥ √2 , light incident at any angle shall be guided along a length perpendicular to the incident face.
Let the ray incident on face AB at angle i, after refraction, it travels along PQ and then interact with face AC which is perpendicular to the incident face.
Any ray is guided along AC if the angle ray makes with the face AC(φ) is greater than the critical angle. From figure
φ + r = 90°, therefore sin φ = cos r ...(i)
If φ is the critical angle it means, sin...(ii)
From (i) and (ii),
i.e.,...(iii)
Applying Snell's law on face AB,
1 . sin i = μ sin r
or...(iv)
From (i) and (ii),
or sin2i ≤ μ2 - 1 ...(v)
When i = π/2, then we have smallest angle φ.
If it is greater than the critical angle, then all other angles of incidence shall be more than the critical angle.
Thus 1 ≤ μ2 - 1 or μ2 ≥ 2
⇒ μ ≥ √2. This is the required result.
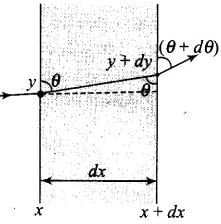
Q.29. The mixture a pure liquid and a solution in a long vertical column (i.e, horizontal dimensions << vertical dimensions) produces diffusion of solute particles and hence a refractive index gradient along the vertical dimension. A ray of light entering the column at right angles to the vertical is deviated from its original path. Find the deviation in travelling a horizontal distance d << h, the height of the column.
Let us consider a portion of a ray between x and x + dx inside the liquid solution. Let the angle of incidence of ray at x be θ and let the ray enters the thin column at height y. Because of the refraction it deviates from the original path and emerges at x + dx with an angle θ + dθ and at a height y + dy.
From Snell's law,
...(i)
Let refractive index of the liquid at position y be μ(y) = μ, then
where k = (dμ/dy) = refractive index gradient along the vertical dimension.
Hence from (i), μ sin θ = (μ + kdy) . sin (θ + dθ)
μ sin θ = (μ + kdy) . (sin θ . cos dθ + cos θ . sin dθ)
μ sin θ = (μ + kdy) . (sin θ . 1 + cos θ . dθ) ...(ii)
For small angle sin dθ ≈ dθ and cos dθ ≈ 1
μ sin θ = μ sin θ + kdy sin θ + μ cos θ . dθ + k cos θ dy.dθ
kdy sin θ + μ cos θ . dθ = 0 ⇒ dθ = (-k/μ) tan θ dy
But
Integrating both sides,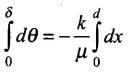
⇒
Q.30. If light passes near a massive object, the gravitational interaction causes a bending of the ray. This can be thought of as happening due to a change in the effective refractive index of the medium given by
n(r) = 1 + 2 GM/rc2
where r is the distance of the point of consideration from the centre of the mass of the massive body, G is the universal gravitational constant, M the mass of the body and c the speed of light in vacuum. Considering a spherical object find the deviation of the ray from the original path as it grazes the object.
Let us consider two spherical surfaces of radius r and r + dr. Let the light be incident at an angle θ at the surface at r and leave r + dr at an angle θ + dθ. Then from Snell's law,
n(r) sin θ = n(r + dr) sin (θ + dθ)
⇒
For small angle, sin dθ ≈ dθ and cos dθ ≈ 1
Ignoring the product of differentials
⇒
or we have,
Now, r2 = x2 + R2 and tan θ = R/x
2rdr = 2xdx
Now substitution for integrals, we have
Put x = R tan φ
dx = R sec2φ dφ
∴
⇒This is the required proof.
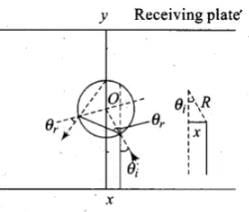
Q.31. An infinitely long cylinder of radius R is made of an unusual exotic material with refractive index –1 (Fig.). The cylinder is placed between two planes whose normals are along the y direction. The center of the cylinder O lies along the y-axis. A narrow laser beam is directed along the y direction from the lower plate. The laser source is at a horizontal distance x from the diameter in the y direction. Find the range of x such that light emitted from the lower plane does not reach the upper plane.
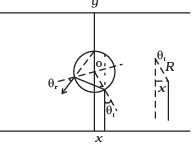
Here the material has refractive index -1, θr is negative and θ'r positive.
Now,
The total deviation of the outcoming ray from the incoming ray is 4θr Rays shall not reach the receiving plate if
[angles measured clockwise from the y-axis]
On solving,
Now,
or
Thus, for light emitted from the source shall not reach the receiving plate.
If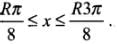
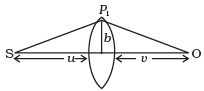
Q.32. (i) Consider a thin lens placed between a source (S) and an observer (O) (Fig.). Let the thickness of the lens vary as w(b) = ω0 - (b2/α), where b is the verticle distance from the pole. ω0 is a constant. Using Fermat’s principle i.e. the time of transit for a ray between the source and observer is an extremum, find the condition that all paraxial rays starting from the source will converge at a point O on the axis. Find the focal length.
(ii) A gravitational lens may be assumed to have a varying width of the form
w(b) = k1ln(k2 / b) bmin < b < bmax
= k1ln(k2 / bmin) b < bmin
Show that an observer will see an image of a point object as a ring about the center of the lens with an angular radius 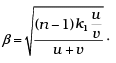
(i) The time taken by ray to travel from S to P1 is
t1 = SP1 / c =
or t1 = u / c (1 + 1 / 2 . b2 / u2) assuming b << 1.
The time required to travel from P1 to O is
The time required to travel through the lens is
t3 = (n - 1)w(b) / c
where n is the refractive index.
Thus, the total time is
t = 1 / c[u + v + 1 / 2 b2(1 / u + 1 / v) + (n - 1)w(b)]
Put 1 / D = 1 / u + 1 / v
Then, t = 1 / c (u + v + 1 / 2 . b2 / D + (n - 1)(w0 + b2 / ∝))
Fermat's principle gives the time taken should be minimum.
For that first derivative should be zero.
dt / db = 0 = b / CD - 2(n - 1)b / c∝
∝ = 2(n - 1)D
Thus, a convergent lens is formed if α = 2(n - 1)D. This is independent of and hence all paraxial rays from S will converge at O i.e., for rays b << n and b << v.
Since, 1 / D = 1 / u + 1 / v, the focal length is D.
(ii) In this case, differentiating expression of time taken t w.r.t.b.
Thus, all rays passing at a height b shall contribute to the image. The ray paths make an angle.This is the required expression.
|
74 videos|314 docs|88 tests
|
FAQs on NCERT Exemplar: Ray Optics & Optical Instruments - Physics Class 12 - NEET
| 1. What is ray optics? |  |
| 2. What are optical instruments? |  |
| 3. How does reflection occur in ray optics? |  |
| 4. What is refraction in ray optics? |  |
| 5. How do optical instruments work? |  |