NCERT Exemplar - Relations and Functions (Part - 1) | Mathematics (Maths) Class 12 - JEE PDF Download
SHORT ANSWER TYPE QUESTIONS
Q.1. Let A = {a, b, c} and the relation R be defined on A as follows:
R = {(a, a), (b, c), (a, b)}.
Then, write minimum number of ordered pairs to be added in R to make R reflexive and transitive.
Ans.
Here, R = {(a, a), (b, c), (a, b)}
for reflexivity; (b, b), (c, c) and for transitivity; (a, c)
Hence, the required ordered pairs are (b, b), (c, c) and (a, c)
Q.2. Let D be the domain of the real valued function f defined by 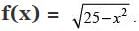
Then, write D.
Ans.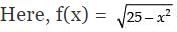
For real value of f(x), 25 – x2 ≥ 0
⇒ – x2 ≥ – 25 ⇒ x2 ≤ 25 ⇒ - 5 ≤ x ≤ 5
Hence, D ∈ - 5 ≤ x ≤ 5 or [- 5, 5]
Q.3. Let f, g : R → R be defined by f (x) = 2x + 1 and g (x) = x2 – 2, ∀ x ∈ R, respectively. Then, find gof.
Ans.
Here, f(x) = 2x + 1 and g(x) = x2 – 2
∴ g of = g[f(x)]
= [2x + 1]2 – 2 = 4x2 + 4x + 1 – 2 = 4x2 + 4x – 1
Hence, g of = 4x2 + 4x – 1
Q.4. Let f: R → R be the function defined by f (x) = 2x – 3 ∀ x ∈ R. write f –1.
Ans.
Here, f(x) = 2x – 3
Let f(x) = y = 2x – 3
⇒ y + 3 = 2x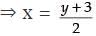
Q.5. If A = {a, b, c, d} and the function f = {(a, b), (b, d), (c, a), (d, c)}, write f -1.
Ans.
Let y = f(x) ∴ x = f – 1(y)
∴ If f = {(a, b), (b, d), (c, a), (d, c)}
then f – 1 = {(b, a), (d, b), (a, c), (c, d)}
Q.6. If f: R → R is defined by f (x) = x2 – 3x + 2, write f (f (x)).
Ans.
Here, f(x) = x2 – 3x + 2
∴ f [f(x)] = [f(x)]2 – 3f(x) + 2
= (x2 – 3x + 2)2 – 3(x2 – 3x + 2) + 2
= x4 + 9x2 + 4 – 6x3 + 4x2 – 12x – 3x2 + 9x – 6 + 2
= x4 – 6x3 + 10x2 – 3x
Hence, f [f(x)] = x4 – 6x3 + 10x2 – 3x
Q.7. Is g = {(1, 1), (2, 3), (3, 5), (4, 7)} a function? If g is described by
g (x) = αx + β, then what value should be assigned to α and β.
Ans.
Yes, g = {(1, 1), (2, 3), (3, 5), (4, 7)} is a function.
Here, g(x) = αx + β
For (1, 1), g(1) = α.1 + β
1 = α + β ... (1)
For (2, 3), g(2) = α.2 + β
3 = 2α + β ... (2)
Solving eqs. (1) and (2) we get, α = 2, β = – 1
Q.8. Are the following set of ordered pairs functions? If so, examine whether the mapping is injective or surjective.
(i) {(x, y): x is a person, y is the mother of x}.
(ii){(a, b): a is a person, b is an ancestor of a}.
Ans.
(i) It represents a function. The image of distinct elements of x under f are not distinct. So, it is not injective but it is surjective.
(ii) It does not represent a function as every domain under mapping does not have a unique image.
Q.9. If the mappings f and g are given by f = {(1, 2), (3, 5), (4, 1)} and g = {(2, 3), (5, 1), (1, 3)}, write fog.
Ans.
fog = f [g(x)]
= f [g(2)] = f(3) = 5
= f [g(5)] = f(1) = 2
= f [g(1)] = f(3) = 5
Hence, fog = {(2, 5), (5, 2), (1, 5)}
Q.10. Let C be the set of complex numbers. Prove that the mapping f: C → R given by f (z) = |z|, ∀ z ∈ C, is neither one-one nor onto.
Ans.
Here, f(z) = |z| ∀ z ∈ C
f(1) = |1| = 1
f(- 1) = |- 1| = 1
f(1) = f(- 1)
But 1 ≠ - 1
Therefore, it is not one-one.
Now, let f(z) = y = |z|. Here, there is no pre-image of negative numbers. Hence, it is not onto.
Q.11. Let the function f: R → R be defined by f (x) = cos x, ∀ x ∈ R. Show that f is neither one-one nor onto.
Ans.
Here, f(x) = cos x ∀ x ∈ R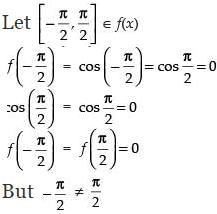
Therefore, the given function is not one-one. Also, it is not onto function as no pre-image of any real number belongs to the range of cos x i.e., [–1, 1].
Q.12. Let X = {1, 2, 3}and Y = {4, 5}. Find whether the following subsets of X × Y are functions from X to Y or not.
(i) f = {(1, 4), (1, 5), (2, 4), (3, 5)}
(ii) g = {(1, 4), (2, 4), (3, 4)}
(iii) h = {(1, 4), (2, 5), (3, 5)}
(iv) k = {(1, 4), (2, 5)}.
Ans.
Here, given that X = {1, 2, 3}, Y = {4, 5}
∴ X × Y = {(1, 4), (1, 5), (2, 4), (2, 5), (3, 4), (3, 5)}
(i) f = {(1, 4), (1, 5), (2, 4), (3, 5)}
f is not a function because there is no unique image of each element of domain under f.
(ii) g = {(1, 4), (2, 4), (3, 4)}
Yes, g is a function because each element of its domain has a unique image.
(iii) h = {(1, 4), (2, 5), (3, 5)}
Yes, it is a function because each element of its domain has a unique image.
(iv) k = {(1, 4), (2, 5)}
Clearly k is also a function.
Q.13. If functions f: A → B and g: B → A satisfy g of = IA, then show that f is one-one and g is onto.
Ans.
Let x1, x2 ∈ gof
gof {f(x1)} = gof {f(x2)}
⇒ g(x1) = g(x2) [∵ gof = IA]
∴ x1 = x2
Hence, f is one-one. But g is not onto as there is no pre-image of A in B under g.
Q.14. Let f: R → R be the function defined by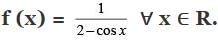
Then, find the range of f.
Ans.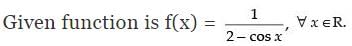
Range of cos x is [– 1, 1]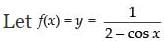
⇒ 2y – y cos x = 1 ⇒ y cos x = 2y – 1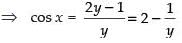
Now – 1 ≤ cos x ≤ 1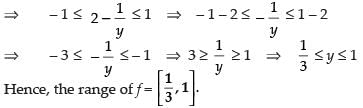
Q.15. Let n be a fixed positive integer. Define a relation R in Z as follows: ∀ a, b ∈ Z, a R b if and only if a – b is divisible by n. Show that R is an equivalence relation.
Ans.
Here, ∀ a, b ∈ Z and a R b if and only if a - b is divisible by n.
The given relation is an equivalence relation if it is reflexive, symmetric and transitive.
(i) Reflexive:
a R a ⇒ (a - a) = 0 divisible by n
So, R is reflexive.
(ii) Symmetric:
a R b = b R a ∀ a, b ∈ Z
a - b is divisible by n (Given)
⇒ - (b - a) is divisible by n
⇒ b – a is divisible by n
⇒ b R a
Hence, R is symmetric.
(iii) Transitive:
a R b and b R c ⇔ a R c ∀ a, b, c ∈ Z
a - b is divisible by n
b - c is also divisible by n
⇒ (a - b) + (b - c) is divisible by n
⇒ (a - c) is divisible by n
Hence, R is transitive.
So, R is an equivalence relation.
LONG ANSWER TYPE QUESTIONS
Q.16. If A = {1, 2, 3, 4}, define relations on A which have properties of being:
(a) Reflexive, transitive but not symmetric
(b) Symmetric but neither reflexive nor transitive
(c) Reflexive, symmetric and transitive.
Ans.
Given that A = {1, 2, 3, 4}
∴ ARA = {(1, 1), (2, 2), (3, 3), (4, 4), (1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4), (2, 1), (3, 1), (4, 1), (3, 2), (4, 2), (4, 3)}
(a) Let R1 = {(1, 1), (2, 2), (1, 2), (2, 3), (1, 3)}
So, R1 is reflexive and transitive but not symmetric.
(b) Let R2 = {(2, 3), (3, 2)}
So, R2 is only symmetric.
(c) Let R3 = {(1, 1), (1, 2), (2, 1), (2, 4), (1, 4)}
So, R3 is reflexive, symmetric and transitive.
Q.17. Let R be relation defined on the set of natural number N as follows: R = {(x, y) : x ∈N, y ∈ N, 2x + y = 41}. Find the domain and range of the relation R. Also verify whether R is reflexive, symmetric and transitive.
Ans.
Given that x ∈ N, y ∈ N and 2x + y = 41
∴ Domain of R = {1, 2, 3, 4, 5, ..., 20}
and Range = {39, 37, 35, 33, 31, ..., 1}
Here, (3, 3) ∈ R
as 2 × 3 + 3 ≠ 41
So, R is not reflexive.
R is not symmetric as (2, 37) ∈ R but (37, 2) ∉R
R is not transitive as (11, 19) ∈ R and (19, 3) ∈ R but (11, 3) ∉ R.
Hence, R is neither reflexive, nor symmetric and nor transitive.
Q.18. Given A = {2, 3, 4}, B = {2, 5, 6, 7}. Construct an example of each of the following:
(a) An injective mapping from A to B
(b) A mapping from A to B which is not injective
(c) A mapping from B to A.
Ans.
Here, A = {2, 3, 4} and B = {2, 5, 6, 7}
(a) Let f: A → B be the mapping from A to B
f = {(x, y): y = x + 3}
∴ f = {(2, 5), (3, 6), (4, 7)} which is an injective mapping.
(b) Let g: A → B be the mapping from A → B such that
g = {(2, 5), (3, 5), (4, 2)} which is not an injective mapping.
(c) Let h: B → A be the mapping from B to A
h = {(y, x): x = y - 2}
h = {(5, 3), (6, 4), (7, 3)} which is the mapping from B to A.
Q.19. Give an example of a map
(i) Which is one-one but not onto
(ii) Which is not one-one but onto
(iii) Which is neither one-one nor onto.
Ans.
(i) Let f: N → N given by f(x) = x2
Let x1, x2 ∈ N then f(x1) = x12 and f(x2) = x22
Now, f (x1) = f(x2) ⇒ x12 =x22 ⇒ x12 -x22= 0 ⇒ (x1 + x2) (x1 - x2) = 0
Since x1, x2 ∈ N, so x1 + x2 = 0 is not possible.
∴ x1 – x2 = 0 ⇒ x1 = x2
∴ f(x1) = f(x2) ⇒ x1 = x2
So, f (x) is one to one function.
Now, Let f(x) = 5 ∈ N
then x2 = 5 ⇒ x = ± √5 ∉ N
So, f is not onto.
Hence, f (x) = x2 is one-one but not onto.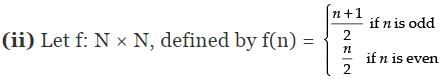
Since f (1) = f(2) but 1 ≠ 2,
So, f is not one-one.
Now, let y ∈ N be any element.
Then f (n) = y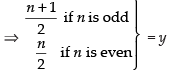
⇒ n = 2y – 1 if y is even
n = 2y if y is odd or even
⇒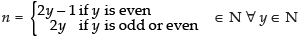
∴ Every y ∈ N has pre-image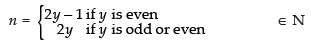
∴ f is onto.
Hence, f is not one-one but onto.
(iii) Let f: R → R be defined as f(x) = x2
Let x1 = 2 and x2 = - 2
f(x1) = x12 = (2)2= 4
f(x2) = x22 = (- 2)2 = 4
f(2) = f(- 2) but 2 ≠ - 2
So, it is not one-one function.
Let f (x) = – 2 ⇒ x2 = – 2 ∴ x = ± √-2 ∉ R
Which is not possible, so f is not onto.
Hence, f is neither one-one nor onto.
Q.20. Let A = R – {3}, B = R – {1}. Let f: A → B be defined by f (x) = (x-2)/(x-3) ∀ x ∈ A . Then show that f is bijective.
Ans.
Here, A ∈ R - {3}, B = R - {1}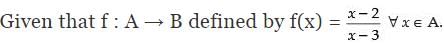
Let x1, x2 ∈ f(x)
∴ f(x1) = f(x2)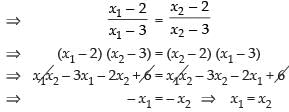
So, it is injective function.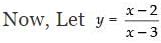
⇒ xy – 3y = x – 2
⇒ xy – x = 3y – 2
⇒ x(y – 1) = 3y – 2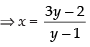
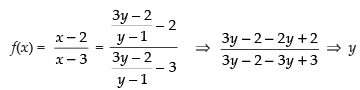
⇒ f(x) = y ∈ B.
So, f (x) is surjective function.
Hence, f (x) is a bijective function.
Q.21. Let A = [–1, 1]. Then, discuss whether the following functions defined on A are one-one, onto or bijective:
(i) f(x) = 2/x
(ii) g(x) = |x|
(iii) h(x) = x |x|
(iv) k(x) = x2
Ans.
(i) Given that – 1 ≤ x ≤ 1
Let x1, x2 ∈ f(x)
So, f(x) is one-one function.
Let f(x) = y = x/2 ⇒ x = 2y
For y = 1, x = 2 ∉ [-1, 1]
So, f (x) is not onto. Hence, f(x) is not bijective function.
(ii) Here, g(x) = |x|
g(x1) = g(x2) ⇒ |x1| = |x2| ⇒ x1 = +x2
So, g (x) is not one-one function.
Let g(x) =y= |x| ⇒ x = + y ∉ A ∀ y ∈ A
So, g (x) is not onto function.
Hence, g (x) is not bijective function.
(iii) Here, h(x) = x|x|
h(x1) = h f(x2)
⇒ x1|x1| = x2|x2| ⇒ x1 = x2
So, h (x) is one-one function.
Now, let h(x) = y = x|x| = x2 or - x2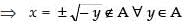
∴ h(x) is not onto function.
Hence, h (x) is not bijective function.
(iv) Here, k(x) = x2 k(x1) = k(x2)
⇒ x12 = x22 ⇒ x1 = ± x2
So, k (x) is not one-one function.
Now, let k(x) = y = x2 ⇒ x = ± √y
If y = – 1 ⇒ x = ± √- 1 ∉ A ∀ y ∈ A
∴ k(x) is not onto function.
Hence, k (x) is not a bijective function.
Q.22. Each of the following defines a relation on N:
(i) x is greater than y, x, y ∈ N
(ii) x + y = 10, x, y ∈ N
(iii) x y is square of an integer x, y ∈ N
(iv) x + 4y = 10 x, y ∈ N.
Determine which of the above relations are reflexive, symmetric and transitive.
Ans.
(i) x is greater than y, x, y ∈ N
For reflexivity x > x ∀ x ∈ N which is not true
So, it is not reflexive relation.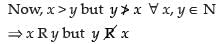
So, it is not symmetric relation.
For transitivity, x R y, y R z ⇒ x R z ∀x, y, z ∈ N ⇒ x > y, y > z ⇒ x > z
So, it is transitive relation.
(ii) Here, R = {(x, y) : x + y = 10 ∀ x, y ∈ N}
R = {(1, 9), (2, 8), (3, 7), (4, 6), (5, 5), (6, 4), (7, 3), (8, 2), (9, 1)}
For reflexive: 5 + 5 = 10, 5 R 5 ⇒ (x, x) ∈ R
So, R is reflexive.
For symmetric: (1, 9) ∈ R and (9, 1) ∈ R
So, R is symmetric.
For transitive: (3, 7) ∈ R, (7, 3) ∈ R but (3, 3) ∉ R
So, R is not transitive.
(iii) Here, R = {(x, y) : xy is a square of an integer, x, y ∈ N}
For reflexive: x R x = x . x = x2 is an integer
[∴ Square of an integer is also an integer]
So, R is reflexive.
For symmetric: x R y = y R x ∀ x, y ∈ N
∴ xy = yx (integer)
So, it is symmetric.
For transitive: x R y and y R z ⇒ x R z
Let xy = k2 and yz = m2
which is again a square of an integer.
So, R is transitive.
(iv) Here, R = {(x, y) : x + 4y = 10, x, y ∈ N}
R = {(2, 2), (6, 1)}
For reflexivity: (2, 2) ∈ R
So, R is reflexive.
For symmetric: (x, y) ∈ R but (y, x) ∉ R (6, 1) ∈ R but (1, 6) ∉ R
So, R is not symmetric.
For transitive: (x, y) ∈ R but (y, z) ∉ R and (x, z) ∈ R
So, R is not transitive.
Q.23. Let A = {1, 2, 3, ... 9} and R be the relation in A × A defined by (a, b) R (c, d) if a + d = b + c for (a, b), (c, d) in A × A. Prove that R is an equivalence relation and also obtain the equivalent class [(2, 5)].
Ans.
Here, A = {1, 2, 3, ..., 9}
and R → A × A defined by (a, b) R (c, d) ⇒ a + d = b + c
∀ (a, b), (c, d) ∈ A × A
For reflexive: (a, b) R (a, b) = a + b = b + a ∀ a, b ∈ A which is true. So, R is reflexive.
For symmetric: (a, b) R (c, d) = (c, d) R (a, b)
L.H.S. a + d = b + c
R.H.S. c + b = d + a
L.H.S. = R.H.S. So, R is symmetric.
For transitive: (a, b) R (c, d) and (c, d) R (e, f) ⇔ (a, b) R (e, f)
⇒ a + d = b + c and c + f = d + e
⇒ a + d = b + c and d + e = c + f
⇒ (a + d) - (d + e) = (b + c) - (c + f)
⇒ a - e = b - f
⇒ a + f = b + e
⇒ (a, b) R (e, f)
So, R is transitive.
Hence, R is an equivalence relation.
Equivalent class of {(2, 5)} is {(1, 4), (2, 5), (3, 6), (4, 7), (5, 8), (6, 9)}
Q.24. Using the definition, prove that the function f : A → B is invertible if and only if f is both one-one and onto.
Ans.
A function f : X → Y is said to be invertible if there exists a
function g : Y → X such that gof = IX and fog = IY and then the inverse of f is denoted by
f -1.
A function f : X → Y is said to be invertible if f is a bijective function.
Q.25. Functions f, g : R → R are defined, respectively, by f (x) = x2 + 3x + 1, g (x) = 2x – 3, find
(i) fog
(ii) gof
(iii) fof
(iv) gog
Ans.
(i) fog ⇒ f[g(x)] = [g(x)]2 + 3[g(x)] + 1
= (2x – 3)2 + 3(2x – 3) + 1 = 4x2 + 9 – 12x + 6x – 9 + 1 = 4x2 – 6x + 1
(ii) gof ⇒ g[f(x)] = 2[x2 + 3x + 1] – 3 = 2x2 + 6x + 2 – 3 = 2x2 + 6x – 1
(iii) fof ⇒ f[f(x)] = [f(x)]2 + 3[f(x)] + 1
= (x2 + 3x + 1)2 + 3(x2 + 3x + 1) + 1
= x4 + 9x2 + 1 + 6x3 + 6x + 2x2 + 3x2 + 9x + 3 + 1
= x4 + 6x3 + 14x2 + 15x + 5
(iv) gog ⇒ g[g(x)] = 2[g(x)] – 3 = 2(2x – 3) – 3 = 4x – 6 – 3 = 4x – 9
Q.26. Let * be the binary operation defined on Q. Find which of the following binary operations are commutative
(i) a * b = a – b ∀ a, b ∈ Q
(ii) a * b = a2 + b2 ∀ a, b ∈ Q
(iii) a * b = a + ab ∀ a, b ∈ Q
(iv) a * b = (a – b)2 ∀ a, b ∈ Q
Ans.
(i) a * b = a – b ∈ Q ∀ a, b ∈ Q.
So, * is binary operation.
a * b = a – b and b * a = b – a ∀ a, b ∈ Q
a - b ≠ b - a
So, * is not commutative.
(ii) a * b = a2 + b2 ∈ Q,
so * is a binary operation. a * b = b * a
⇒ a2 + b2 = b2 + a2 ∀ a, b ∈ Q Which is true.
So, * is commutative.
(iii) a * b = a + ab ∈ Q, so * is a binary operation.
a * b = a + ab and b * a = b + ba
a + ab ≠ b + ba ⇒ a * b ≠ b * a ∀ a, b ∈ Q.
So, * is not commutative.
(iv) a * b = (a – b)2 ∈ Q, so * is binary operation.
a * b = (a - b)2 and b * a = (b - a)2 a * b = b * a
⇒ (a - b)2 = (b - a)2 ∀ a, b ∈ Q.
So, * is commutative.
Q.27. Let * be binary operation defined on R by a * b = 1 + ab, ∀ a, b ∈ R. Then the operation * is
(i) Commutative but not associative
(ii) Associative but not commutative
(iii) Neither commutative nor associative
(iv) Both commutative and associative
Ans.
(i): Given that
a * b = 1 + ab ∀ a, b ∈ R
and b * a = 1 + ba ∀ a, b ∈ R
a * b = b * a = 1 + ab
So, * is commutative.
Now a * (b * c) = (a * b) * c ∀ a, b, c ∈ R
L.H.S. a * (b * c) = a * (1 + bc) = 1 + a(1 + bc) = 1 + a + abc
R.H.S. (a * b) * c = (1 + ab) * c = 1 + (1 + ab) . c = 1 + c + abc
L.H.S. ≠ R.H.S.
So, * is not associative.
Hence, * is commutative but not associative.
|
203 videos|307 docs|139 tests
|
FAQs on NCERT Exemplar - Relations and Functions (Part - 1) - Mathematics (Maths) Class 12 - JEE
| 1. What are relations and functions in mathematics? |  |
| 2. How do you determine if a relation is a function? |  |
| 3. What is the domain and range of a function? |  |
| 4. How do you find the inverse of a function? |  |
| 5. What are the different types of functions? |  |
















