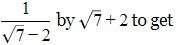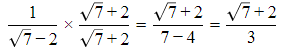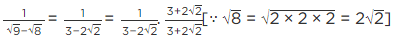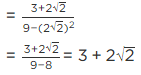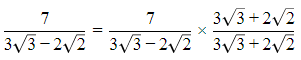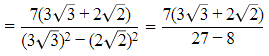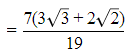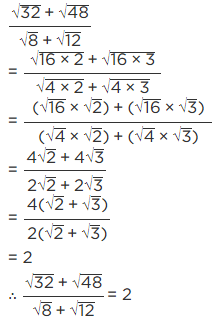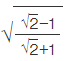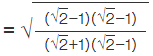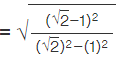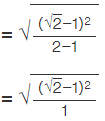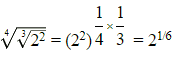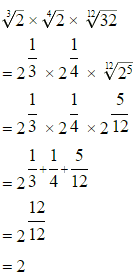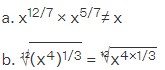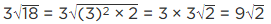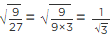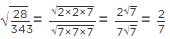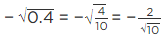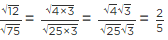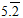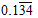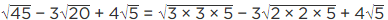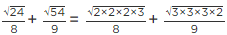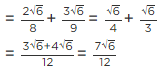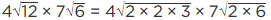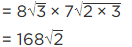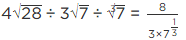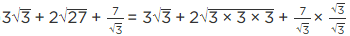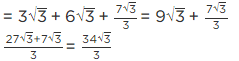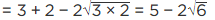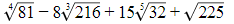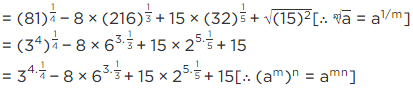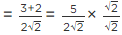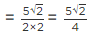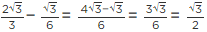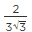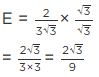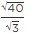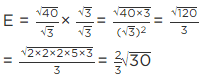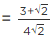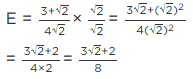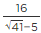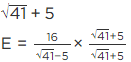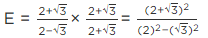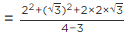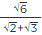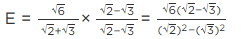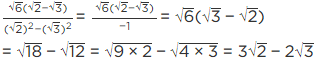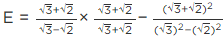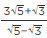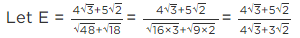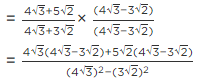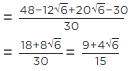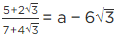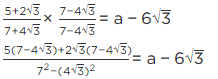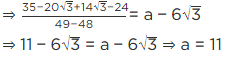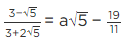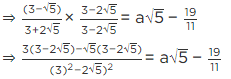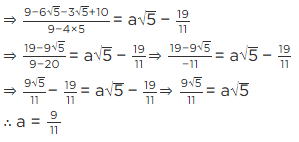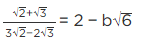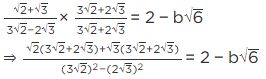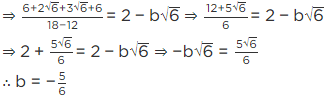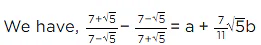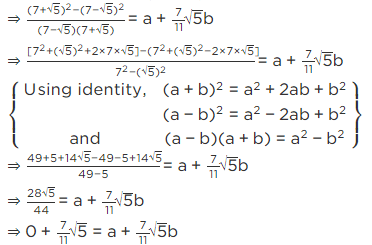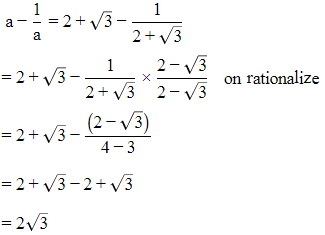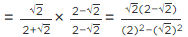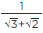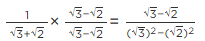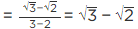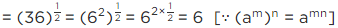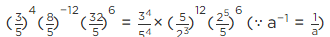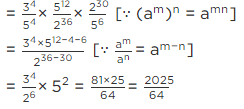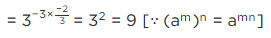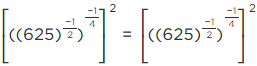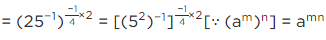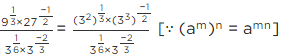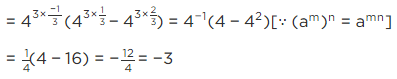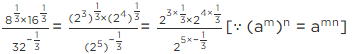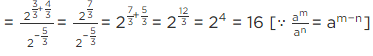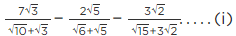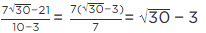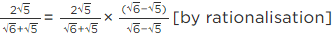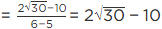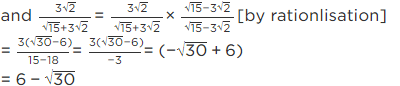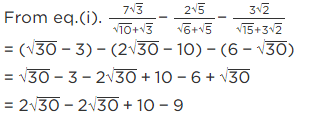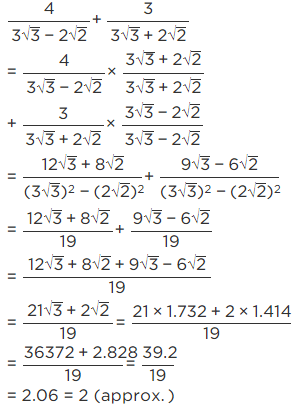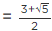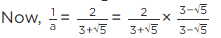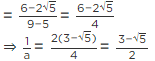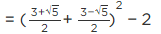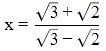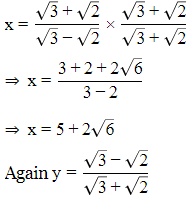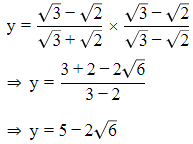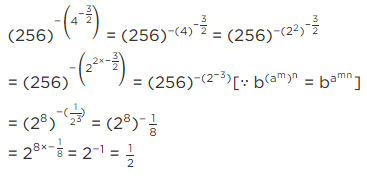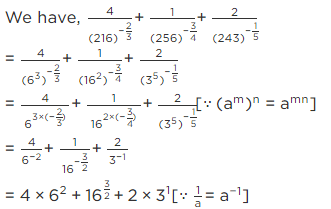NCERT Exemplar Solutions: Number System | Mathematics (Maths) Class 9 PDF Download
Exercise 1.1
Write the correct answer in each of the following:
Q.1. Every rational number is
(a) a natural number
(b) an integer
(c) a real number
(d) a whole number
Correct Answer is Option (c)
We know that rational and irrational numbers taken together are known as real numbers. Therefore, every real number is either a rational number or an irrational number. Hence, every rational number is a real number. Hence, (c) is the correct option.
Q.2. Between two rational numbers
(a) there is no rational number
(b) there is exactly one rational number
(c) there are infinitely many rational numbers
(d) there are only rational numbers and no irrational numbers
Correct Answer is Option (c)
Between two rational numbers there are infinitely many rational number. Hence, (c) is the correct option.
Q.3. Decimal representation of a rational number cannot be
(a) terminating
(b) non-terminating
(c) non-terminating repeating
(d) non-terminating non-repeating
Correct Answer is Option (d)
The decimal representation of a rational number cannot be non-terminating and non- repeating. Hence, (d) is the correct option
Q.4. The product of any two irrational numbers is
(a) always an irrational number
(b) always a rational number
(c) always an integer
(d) sometimes rational, sometimes irrational
Correct Answer is Option (d)
The product of any two irrational numbers is sometimes rational and sometimes irrational. Hence, (d) is the correct option
Q.5. The decimal expansion of the number √2 is
(a) a finite decimal
(b) 1.41421
(c) non-terminating recurring
(d) non-terminating non-recurring
Correct Answer is Option (d)
The approximate value of √2 is1.141421 this can be verified by division method.
Since √2 is an irrational number
Decimal Expansion of √2 is Non-Terminating non-repeating.
Hence option (D) is the correct option.
Q.6. Which of the following is irrational?
(a) √4/√9
(b) √12/√3
(c) √7
(d) √81
Correct Answer is Option (c)
(a) √4/√9 = 2/3
(b) √12/√3 = 2√3/√3 = 2
(c) √7 = 2.64575131106
(d) √81 = 9
Here, (c) √7 = 2.64575131106, is a non terminating decimal expansion. Hence, (C) is the correct option
Q.7. Which of the following is irrational?
(a) 0.14
(b)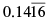
(c) 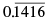
(d) 0.4014001400014...
Correct Answer is Option (d)
A number is irrational if and only of its decimal representation is non-terminating and non-recurring.
(a) is a terminating decimal and therefore cannot be an irrational number.
(b) is a non-terminating and recurring decimal and therefore cannot be irrational.
(c) is a non-terminating and recurring decimal and therefore cannot be irrational.
(d) is a non-terminating and non-recurring decimal and therefore is an irrational number.
Hence, (d) is the correct option.
Q.8. A rational number between √2 and √3 is
(a) 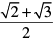
(b) 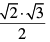
(c) 1.5
(d) 1.8
Correct Answer is Option (c)
√2 =1.4142135…. and √3 =1.732050807….
(a) (√2+√3)/2 = 1.57313218497… is a non-terminating and non-recurring decimal and therefore is an irrational number.
(b) (√2. √3)/2 = 1.22474487139… is a non-terminating and non-recurring decimal and therefore is an irrational number.
(c) 1.5 is a terminating decimal and therefore is a rational number.
(d) 1.8 is a terminating decimal and therefore is a rational number.
Here both 1.5 and 1.8 are rational numbers. But, 1.8 does not lie in between √2 =1.4142135…. and √3 =1.732050807…. Whereas 1.5 lies in between √2 =1.4142135…. and √3 =1.732050807….
Hence, (c) is the correct option.
Q.9. The value of 1.999… in the form p/q, where p and q are integers and q ≠ 0 , is
(a) 19/10
(b) 1999/1000
(c) 2
(d) 1/9
Correct Answer is Option (c)
(a) 19/10 = 1.9
(b) 1999/1000= 1.999
(c) 2
(d) 1/9= 0.111….
Let x = 1.9999….. — (1)
Multiply equation (1) with 10
10x = 19.9999….. — (2)
Subtract equation (1) from equation(2) ,
We get,
9x = 18
x = 18 / 9
x = 2
Therefore,
x = 1.9999… = 2
Hence, (c) is the correct option.
Q.10. 2√3 + √3 is equal to
(a) 2√6
(b) 6
(c) 3√3
(d) 4√6
Correct Answer is Option (c)
2√3 + √3
Taking √3 common,
We get,
√3(2+1) = √3(3) = 3√3
Hence, (c) is the correct option.
Q.11. √10 × √15 is equal to
(a) 6√5
(b) 5√6
(c) 2√5
(d) 10√5
Correct Answer is Option (b)
Given
√10 × √15
It can be written as
= √(2 × 5) × √(5 × 3)
We know that √ab = √a × √b
= 5 × √(2 × 3)
= 5√6
Therefore, √10 × √15 is equal to 5√6.
Q.12. The number obtained on rationalising the denominator of 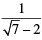 is
is
(a) 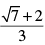
(b) 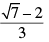
(c) 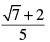
(d) 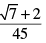
Correct Answer is Option (a)
We use the identity (a + √b) (a - √b) = a2 - b
Multiply and divide
Q.13. 1/(√9 - √8) is equal to
(a) 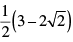
(b) 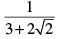
(c) 3– 2√2
(d) 3 + 2√2
Correct Answer is Option (d)
[Multiplying numerator and denominator by 3 + 2√2]
[Using identity (a - b) (a + b) = a2 - b2]
Q.14. After rationalising the denominator of 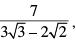 we get the denominator as
we get the denominator as
(a) 13
(b) 19
(c) 5
(d) 35
Correct Answer is Option (b)
Therefore, we get the denominator as 19.
Hence, (B) is the correct answer.
Q.15. The value of 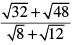 is equal to
is equal to
(a) √2
(b) 2
(c) 4
(d) 8
Correct Answer is Option (b)
Hence, The correct Option is B.
Q.16. If √2 = 1.4142, then 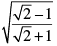 is equal to
is equal to
(a) 2.4142
(b) 5.8282
(c) 0.4142
(d) 0.1718
Correct Answer is Option (c)
Given
√2 = 1.4142
Let us multiply both numerator and denominator by √2 -1
Using the algebraic identity (a + b) (a - b) = a² - b²
By further calculation
So we get
= √2 - 1
Let us substitute the value of √2
= 1.4142 - 1
= 0.4142
Therefore,is equal to 0.4142.
Q.17. 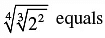
(a)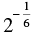
(b) 2– 6
(c) 21/6
(d) 26
Correct Answer is Option (c)
Q.18. The product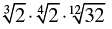 equals
equals
(a) √2
(b) 2
(c)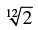
(d)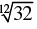
Correct Answer is Option (b)
Hence, option B is the correct answer.
Q.19. Value of 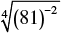 is
is
(a) 1/9
(b) 1/3
(c) 9
(d) 1/81
Correct Answer is Option (a)
Given
∜(81)-2
It can be written as
= 81-2 × 1/4
= 81-1/2
By further calculation
= (√81)-1
= 9-1
= 1/9
Therefore, the value is 1/9.
Q.20. Value of (256)0.16 × (256)0.09 is
(a) 4
(b) 16
(c) 64
(d) 256.25
Correct Answer is Option (a)
Given
(256)0.16 × (256)0.09
It can be written as
= (256)16/100 × (256)9/100
Using am × an = am + n
= 256 16/100 + 9/100
= 25625/100
So we get
= 2561/4
= (44)1/4
We know that [am]n = amn
= 4
Therefore, the value is 4.
Q.21. Which of the following is equal to x?
(a) 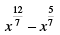
(b) 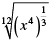
(c) 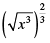
(d) 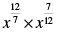
Correct Answer is Option (c)
Let us simplify each option
It can be written as
= (x4/3)1/12
= x4/3 × 1/12
So we get
= x1/9
≠ x
c. [(x3)1/2]2/3 = x3/2 × 2/3 = x1 = x
d. x12/7 × x7/12 = x12/7 + 7/12 = x193/84 ≠ x
Therefore, [(x3)1/2 ]2/3 is equal to x.
Exercise 1.2
Q.1. Let x and y be rational and irrational numbers, respectively. Is x + y necessarily an irrational number? Give an example in support of your answer.
Yes, if x and y are rational and irrational numbers, respectively, then x+ y is an irrational number.
For example,
Let x = 5 and y = √2.
Then, x+y = 5 + √2 = 5 + 1.414… = 6.414…
Here, 6.414 is a non-terminating and non-recurring decimal and therefore is an irrational number.
Hence, x + y is an irrational number.
Q.2. Let x be rational and y be irrational. Is xy necessarily irrational? Justify your answer by an example.
No, if x is rational number and y is irrational number, then, xy is not necessarily an irrational number. It can be rational if x = 0, which is a rational number.
For Example:
Let y = √2, which is irrational.
Consider x = 2, which is rational.
Then, x × y = 2 × √2 = 2√2, which is irrational.
Consider x = 0, which is rational.
Then xy = 0 × √2 = 0, which is rational.
∴, we can conclude that, the product of a rational and an irrational number is always irrational, only if the rational number is not zero.
Q.3. State whether the following statements are true or false? Justify your answer.
(i) √2/3 is a rational number.
(ii) There are infinitely many integers between any two integers.
(iii) Number of rational numbers between 15 and 18 is finite.
(iv) There are numbers which cannot be written in the form p/q, p ≠ 0,p and q both are integers.
(v) The Square of an irrational number is always rational.
(vi) √12/√3 is not a rational number as √12 and √3 are not integers.
(vii) √15/√3 is written in the form p/q, q ≠ 0 and so it is a rational number.
(i) False. Here √2 is an irrational number and 3 is a rational number. We know that when we divide an irrational number by a non-zero rational number, it will always give an irrational number.
(ii) False. Because between two consecutive integers (like 1 and 2) there does not exist any other integer.
(iii) False. Because between any two rational numbers there exist infinitely many rational numbers.
(iv) True. Because there are infinitely many numbers which cannot be written in the formboth are integers and these numbers are called irrational numbers.
(v) False. e.g. Let's consider following irrational numbers.
(a) (√2)2 = 2, which is a rational number.
(b) (∜2)2 = √2 which is not a rational number.
Hence, square of an irrational number is not always a rational number.
(vi) False.which is a rational number.
(vii) False.which is an irrational number.
Q.4. Classify the following numbers as rational or irrational with justification :
(i) 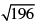
(ii) 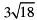
(iii) 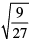
(iv) 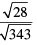
(v) 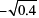
(vi) 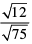
(vii) 0.5918
(viii) (1 + √5) – (4 + √5)
(ix) 10.124124...
(x) 1.010010001...
To classify, use the definition a rational number is in the form of p/q, where p and q are integers and q ≠ 0 and otherwise it is an irrational number.
(i)
Hence, it is a rational number.
(ii)
Hence, it is an irrational number.
(iii)
Hence, it is an irrational number, because √3 is an irrational number.
(iv)
Hence, it is a rational number.
(v)
Hence, it is an irrational number, because √10 is an irrational number.
(vi)
Hence, it is a rational number.
(vii) 0.5918, it is a number with terminating decimal, so it can be written in the form of p/q , where q ≠ 0, p and q are integers. Hence, it is a rational number.
(viii) (1 + √5)−(4 + √5) = 1 − 4 + √5 − √5 = −3
Hence, it is a rational number.
(ix) 10.124124…. is a number with non-terminating recurring decimal expansion.
Hence, it is a rational number.
(x) 1.010010001 …….. is a number with non-terminating non-recurring decimal expansion.
Hence, it is an irrational number.
Exercise 1.3
Q.1. Find which of the variables x, y, z and u represent rational numbers and which irrational numbers:
(i) x2 = 5
(ii) y2 = 9
(iii) z2 = .04
(iv) u2 = 17/4
(i) x2 = 5
On solving, we get
⇒ x = ± √5
Hence, x is an irrational number.
(ii) y2 = 9
On solving, we get
⇒ y = ± 3
Hence, y is a rational number.
(iii) z2 = .04
On solving, we get
⇒ z = ± 0.2
Hence, z is a rational number.
(iv) u2 = 17/4
On solving, we get
⇒ u = ± √17/2
√17 is irrational.
Hence, u is an irrational number
Q.2. Find three rational numbers between
(i) –1 and –2
(ii) 0.1 and 0.11
(iii) 5/7 and 6/7
(iv) 1/4 and 1/5
(i) –1 and –2
Three rational numbers between –1 and –2 are –1.1, –1.2 and –1.3.
(ii) 0.1 and 0.11
Three rational numbers between 0.1 and 0.11 are 0.101, 0.102 and 0.103.
(iii) 5/7 and 6/7
5/7 can be written as (5 × 10)/(7 × 10) = 50/70
Similarly,
6/7 can be written as (6 × 10)/(7 × 10) = 60/70
Three rational numbers between 5/7 and 6/7 = three rational numbers between 50/70 and 60/70.
Three rational numbers between 5/7 and 6/7 are 51/70, 52/70, 53/70.
(iv) 1/4 and 1/5
Here, according to the question,
LCM of 4 and 5 is 20.
Let us make the denominators common, 80.
(4 × 20) = 80 and (5 × 16) = 80
Hence,
1/4 can be written as (1 × 20)/(4 × 20) = 20/80
Similarly,
1/5 can be written as (1 × 16)/(5 × 16) = 16/80
Three rational numbers between 1/4 and 1/5 = three rational numbers between 16/80 and 20/80.
Therefore, the three rational numbers are 17/80, 18/80 and 19/80.
Q.3. Insert a rational number and an irrational number between the following:
(i) 2 and 3
(ii) 0 and 0.1
(iii) 1/3 and 1/2
(iv) – 2/5 and 1/2
(v) 0.15 and 0.16
(vi) √2 and √3
(vii) 2.357 and 3.121
(viii) .0001 and .001
(ix) 3.623623 and 0.484848
(x) 6.375289 and 6.375738.
(i) 2 and 3
So, rational number between 2 and 3 = 2.5
And, irrational number between 2 and 3 = 2.040040004…
(ii) 0 and 0.1
So, rational number between 0 and 0.1 = 0.05
And, irrational number between 0 and 0.1 = 0.007000700007…
(iii) 1/3 and 1/2
LCM of 3 and 2 is 6.
1/3 = 0.33
1/3 can be written as (1 × 20)/(3 × 20) = 20/60
½ = 0.5
1/2 can be written as (1 × 30)/(2 × 30) = 30/60
So, rational number between 1/3 and 1/2 = 25/60
And, irrational number between 1/3 and 1/2 = irrational number between 0.33 and 0.5 = 0.414114111…
(iv) – 2/5 and 1/2
LCM of 5 and 2 is 10.
-2/5 = -0.4
-2/5 can be written as (-2 × 2)/(5 × 2) = -4/10
1/2 = 0.5
1/2 can be written as (1 × 5)/(2 × 5) = 5/10
So, rational number between -2/5 and 1/2 = rational number between -4/10 and 5/10 = 1/10
And, irrational number between -2/5 and 1/2 = irrational number between -0.4 and 0.5 = 0.414114111…
(v) 0.15 and 0.16
Rational number between 0.15 and 0.16 = 0.151
Irrational number between 0.15 and 0.16 = 0.151551555…
(vi) √2 = 1.41 and √3 = 1.732
Rational number between √2 and √3 = rational number between 1.41 and 1.732 = 1.5
Irrational number between √2 and √3 = irrational number between 1.41 and 1.732 = 1.585585558…
(vii) 2.357 and 3.121
Rational number between 2.357 and 3.121 = 3
Irrational number between 2.357 and 3.121 = 3.101101110…
(viii) .0001 and .001
Rational number between .0001 and .001 = 0.00011
Irrational number between .0001 and .001 = 0.0001131331333…
(ix) 3.623623 and 0.484848
Rational number between 3.623623 and 0.484848 = 1
Irrational number between 3.623623 and 0.484848 = 1.909009000…
(x) 6.375289 and 6.375738.
Rational number between 6.375289 and 6.375738 = 6.3753
Irrational number between 6.375289 and 6.375738 = 6.375414114111…
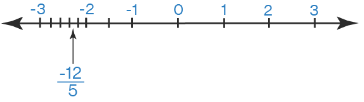
Q.4. Represent the following numbers on the number line:
7, 7.2, −3/2 , −12/5
Given, the numbers are 7, 7.2, -3/2 and -12/5
We have to represent the numbers on the number line.
(a) Number line of 7
First draw a number line whose midpoint is 0.
Mark positive numbers on the right hand side.
Mark negative numbers on the left hand side.(b) Number line of 7.2
First draw a number line whose midpoint is 0.
Mark positive numbers on the right hand side.
Mark negative numbers on the left hand side.(c) Number line of -3/2
-3/2 = -1.5
First draw a number line whose midpoint is 0.
Mark positive numbers on the right hand side.
Mark negative numbers on the left hand side.(d) Number line of -12/5
-12/5 = -2.4
First draw a number line whose midpoint is 0.
Mark positive numbers on the right hand side.
Mark negative numbers on the left hand side.
Q.5. Locate √5, √10 and √17 on the number line.
√5 on the number line:
5 can be written as the sum of the square of two natural numbers:
i.e., 5 =1+ 4 =12 + 22
On the number line,
Take OA = 2 units.
Perpendicular to OA, draw BA = 1 unit.
Join OB.
Using Pythagoras theorem,
We have, OB= √5
Draw an arc with centre O and radius OB using a compass such that it intersects the number line at the point C.
Then, we get, C corresponds to √5. Or we can say that OC = √5√10 on the number line:
10 can be written as the sum of the square of two natural numbers:
i.e., 10 =1+ 9 =12 + 32
On the number line,
Take OA = 3 units.
Perpendicular to OA, draw BA = 1 unit.
Join OB.
Using Pythagoras theorem,
We have, OB= √10
Draw an arc with centre O and radius OB using a compass such that it intersects the number line at the point C.
Then, the point C corresponds to √10. Or we can say that OC = √10√17 on the number line:
17 can be written as the sum of the square of two natural numbers:
i.e., 17 =1+ 16 =12 + 42
On the number line,
Take OA = 4 units.
Perpendicular to OA, draw BA = 1 unit.
Join OB.
Using Pythagoras theorem,
We have, OB= √17
Draw an arc with centre O and radius OB using a compass such that it intersects the number line at the point C.
Then, the point C corresponds to √17. Or, we can say that OC = √17
Q.6. Represent geometrically the following numbers on the number line:
(i) √4.5
(ii) √5.6
(iii) √8.1
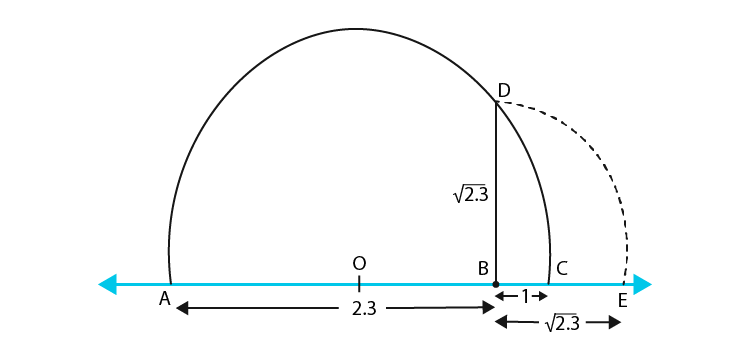
(iv) √2.3
(i) √4.5
Draw a line segment such that AB = 4.5 units.
Mark C at a distance of 1 unit from B.
Mark O, the mid-point of AC.
Draw a semicircle with centre O and radius OC.
Draw a line perpendicular to AC, passing through B and intersecting the semicircle at D.
Now, BD = √4.5.
Draw an arc with centre B and radius BD, meeting AC produced at E.
Then BE = BD = √4.5 units.(ii) √5.6
Draw a line segment such that AB = 5.6 units.
Mark C at a distance of 1 unit from B.
Mark O, the mid-point of AC.
Draw a semicircle with centre O and radius OC.
Draw a line perpendicular to AC, passing through B and intersecting the semicircle at D.
Now, BD = √5.6
Draw an arc with centre B and radius BD, meeting AC produced at E.
Then BE = BD = √5.6 units.(iii) √8.1
Draw a line segment such that AB = 8.1 units.
Mark C at a distance of 1 unit from B.
Mark O, the mid-point of AC.
Draw a semicircle with centre O and radius OC.
Draw a line perpendicular to AC, passing through B and intersecting the semicircle at D.
Now, BD = √8.1.
Draw an arc with centre B and radius BD, meeting AC produced at E.
Then BE = BD = √8.1 units.(iv) √2.3
Draw a line segment such that AB = 2.3 units.
Mark C at a distance of 1 unit from B.
Mark O, the mid-point of AC.
Draw a semicircle with centre O and radius OC.
Draw a line perpendicular to AC, passing through B and intersecting the semicircle at D.
Now, BD = √2.3.
Draw an arc with centre B and radius BD, meeting AC produced at E.
Then BE = BD = √2.3 units.
Q.7. Express the following in the form p/q, where p and q are integers and q ≠ 0:
(i) 0.2
(ii) 0.888…
(iii) 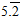
(iv) 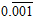
(v) 0.2555…
(vi) 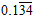
(vii) .00323232…
(viii) .404040…
(i) 0.2
We know that,
0/2 can be written as,
0.2 = 2/10 = 1/5
(ii) 0.888…
Assume that x = 0.888 …
⇒ x = 0.8 ……………. Eq.(1)
Multiply L.H.S and R.H.S by 10,
We get
10 x = 8.8 ……………. Eq.(2)
Subtracting equation (1) from (2),
We get
10 x − x = 8.8 − 0.8
⇒ 9x = 8
⇒ x = 8/9
(iii)
Assume that x = 5.2 ……………. Eq.(1)
Multiply L.H.S and R.H.S by 10,
We get
10 x = 52.2 …………… Eq. (2)
Subtracting equation (1) from (2),
We get
10 x − x = 52.2 − 5.2
⇒ 9x = 47
⇒ x = 47/9
(iv)
Assume that x = 0.001 ……………. Eq. (1)
Multiply L.H.S and R.H.S by 1000,
We get
1000 x = 1.001 …………… Eq. (2)
Subtracting equation (1) from (2),
We get
1000x − x = 1.001 − 0.001
⇒ 999x = 1
⇒ x = 1/999
(v) 0.2555…
Assume that x = 0.2555 …
⇒ x = 0.25 ……………. Eq. (1)
Multiply L.H.S and R.H.S by 10,
We get
10 x = 2.5 ……………. Eq. (2)
Multiply L.H.S and R.H.S by 100,
We get
100 x = 25.5 …………. Eq. (3)
Subtracting equation (2) from (3),
We get
100 x-10x = 25.5 – 2.5
⇒ 90𝑥 = 23
⇒ x = 23/90
(vi)
Let x = 0.134 ………….…. Eq. (1)
Multiply L.H.S and R.H.S by 10,
We get
10 x = 1.34 ………………. Eq. (2)
Multiply L.H.S and R.H.S by 1000,
We get
1000 x = 134.34 …………. Eq. (3)
Subtracting equation (2) from (3),
We get
1000 x − 10x = 134.34 − 1.34
⇒ 990x = 133
⇒ x = 133/990
(vii) .00323232…
Let x = 0.00323232 …
⇒ x = 0.0032 ………….…. Eq. (1)
Multiply L.H.S and R.H.S by 100,
We get,
100x = 0.32 ……………. Eq. (2)
Multiply L.H.S and R.H.S by 10000,
We get
10000 x = 32.32 …………. Eq. (3)
Subtracting equation (2) from (3),
We get
10000 x-100x = 32.32 – 0.32
⇒ 9900x = 32
⇒ x = 32/9900 = 8/2475
(viii) .404040…
Let x = 0.404040 …
⇒ x = 0. 40 ………..….…. (1)
Multiply L.H.S and R.H.S by 100,
We get
100 x = 40.40 ……….…. (2)
Subtracting equation (1) from (2),
We get
100 x − x = 40.40 − 0.40
⇒ 99x = 40
⇒ x = 40/99
Q.8. Show that 0.142857142857... = 1/7
Given, 0.142857142857... = 1/7
We have to prove the above expression.
Considering LHS,
LHS: 0.142857142857...
Let x = 0.142857142857... ________ (1)
Multiplying by 1000000 on both sides,
1000000x = 1000000(0.142857142857... )
1000000x = 142857.142857 _________ (2)
Subtracting (1) and (2),
1000000x - x = 142857.142857 - 0.142857142857
999999x = 142857
x = 142857/999999
x = 1/7
= RHS
LHS = RHS
Hence proved.
Q.9. Simplify the following:
(i) 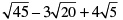
(ii) 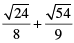
(iii) 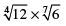
(iv) 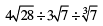
(v) 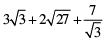
(vi) 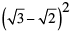
(vii) 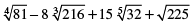
(viii) 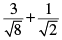
(ix) 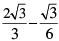
(i)
= 3√5 − 3 × 2√5 + 4√5
= 3√5 − 6√5 + 4√5 = √5
(ii)
(iii)
(iv)
(v)
(vi) (√3 − √2)2 = (√3)2 + (√2)2 − 2√3 × √2 [Using identity (a − b)2 = a2 + b2 − 2ab]
(vii)
= 31 − 8 × 61+ 15 × 21 + 15
= 3 − 48 + 30 + 15
= 48 − 48 = 0
(viii)
[Multiplying numerator and denominator by√2]
(ix)
Q.10. Rationalise the denominator of the following: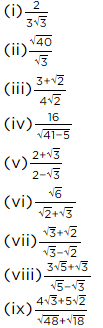
(i) Let E =
For rationalising the denominator, multiply numberator and denominator by √3,
(ii) Let E =
For rationailsing the denominator, multiply numerator and denominator by √3,
(iii) Let E
For rationailsing the denominator, multiply numerator and denominator by √2,
(iv) Let E =
For rationalising the denominator, multiply numerator and denominator by[Using identity, (a − b) (a + b) = a2 − b2]
(v) Let E =
For rationailsing the denominator, multiply numerator and denominator by 2 + √3
[Using identity, (a − b) (a + b) = a2 − b2]
[Using identity (a + b)2 = a2 + 2ab + b2]
= 4 + 3 + 4√3 = 7 + 4√3
(vi) Let E =
For rationalising the denominator, multiply numerator and denominator by √2 − √3
[Using identity, (a − b) (a + b) = a2 − b2]
(vii) For rationalising the denominator, multiply numerator and denominator by √ 3 + √2
[Using identity, (a − b) (a + b) = a2 − b2]
= 3 + 2 + 2√6 = 5 + 2√6
(viii) Let E =
For rationalising the denominator, multiply numerator and denominator by √ 5 + √ 3[Using identity, (a + b) (a − b) = a2 − b2]
(ix)
For rationalising the denominator, multiply numerator and denominator by 4√3 − 3√2,
[Using identity, (a + b) (a − b) = a2 − b2]
Q.11. Find the values of a and b in each of the following:
(i) 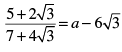
(ii) 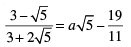
(iii) 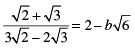
(iii) 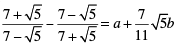
(i) We have
For rationalizing the above equation, we multiply numerator and denominator of LHS by 7 - 4√3 , we get,
[Using identity, (a + b) (a − b) = a2 − b2]
(ii) We have,
For rationalizing the above equation, we multiply numerator and denominator of LHS by 3 − 2√5, we get
[Using identity, (a − b) (a + b) = a2 − b2]
(iii) We have,
For rationalising the above equation, we multiply numerator and denominator of LHS by 3√2 + 2√3 , we get
[Using identity, (a − b) (a + b) = a2 − b2]
(iv)
On comparing both sides, we get
a = 0 and b = 1
Q.12. If a = 2 + 3 , then find the value of 
Given that, a = 2 + √3
Then, Value of
Hence, this is the answer.
Q.13. Rationalise the denominator in each of the following and hence evaluate by taking √2 = 1.414 , √3 = 1.732 and √5 = 2.236 , upto three places of decimal.
(i) 4/√3
(ii) 6/√6
(iii) 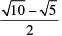
(iv) 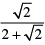
(v) 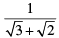
(i) Let E = 4/√3
For rationalising the denominator, multiply numerator and denominator by √3.
We get,
(ii) For rationalising denominator, multiply numerator and denominator by √6.
We get,
= 1.414 × 1.732 = 2.449 [Put √2 = 1.414 and √3 = 1.732]
(iii)
(iv) Let E
For rationalizing the denominator, multiply numerator and denominator by 2 − √2.
We get,
[Using identity, (a − b) (a + b) = a2 − b2]
= √2 − 1 = 1.414 = 0.414 [Put √2 = 1.414]
(v) Let E =
For rationalising the denominator multiply numerator and denominator by √3 − √2.
We get,
[Using identity, (a − b) (a + b) = a2 − b2]
= 1.732 − 1.414 = 0.318 [Put √3 = 1.732 and √2 = 1.414]
Q.14. Simplify:
(i) (13 + 23 + 33)1/2
(ii) (3/5)4 (8/5)-12 (32/5)6
(iii) (1/27)-2/3
(iv) 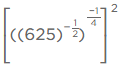
(v) 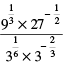
(vi) 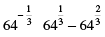
(vii) 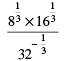
(i) (13 + 23 + 33)1/2 = (1 + 8 + 27)1/2
(ii)
(iii)
(iv)
(v)
(vi)
(vii)
Exercise 1.4
Q.1. Express 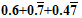 in the form p/q, where p and q are integers and q ≠ 0.
in the form p/q, where p and q are integers and q ≠ 0.
Let x = 0.6
Multiply by 10 on L.H.S and R.H.S,
10x = 6
x = 6/10
x = 3/5
So, the p/q form of 0.6 = 3/5
Let y = 0.77777…
Multiply by 10 on L.H.S and R.H.S,
10y = 7.7777…
10y – y = 7.7777777……. – 0.7777777…………..
9y = 7
y = 7/9
So the p/q form of 0.7777… = 7/9
Let z = 0.47777…
Multiply by 10 on L.H.S and R.H.S,
10z = 4.7777…
10z – z = 4.7777777… – 0.47777777…
9z = 4.2999
z ≈ 4.3/9
z = 43/90
So the p/q form of 0.4777… = 43/90
Therefore, p/q form of is,
x+y+z = 3/5 + 7/9 + 43/90
= (54 + 70 + 43)/90
= 167/90
Q.2. Simplify: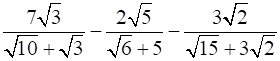
We have,
[Using identity, (a − b) (a + b) = a2 − b2][Using identity , (a − b) (a + b) = a2 − b2]
= 1
Q.3. If √2 = 1.414, √3 = 1.732, then find the value of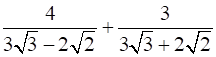
Q.4. If 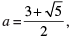 then find the value of
then find the value of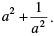
Given, a
[Multiplying numerator and denominator by 3 − √5][Using identity, (a − b) (a + b) = a2 − b2]
[adding and subtracting 2]
= (6/2)2 − 2 = (3)2 − 2 = 9 − 2 = 7
Q.5. If 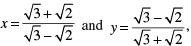 then find the value of x2 + y2.
then find the value of x2 + y2.
Rationalising the denominator, we get
Rationalising the denominator, we get
We know that (x + y)2 = x2 + y2 + 2xy
⇒ x2 + y2 = (x + y)2 −2xy
Substituting the values of x and y we have
⇒ x2 + y2 = (5 + 2√6 + 5 − 2√6 )2 − 2(5 + 2√6 )(5 − 2√6)
=102 −2(25 − 4 × 6)
= 100 − 2(25 − 24)
= 100 − 2(1)
= 100 − 2 = 98
∴ x2 + y2 = 98
Q.6. Simplify : 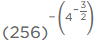
Q.7. Find the value of
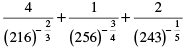
= 4 × 36 + ((4)2)3/2 + 2 × 31
= 4 × 36 + 43 + 6
= 144 + 64 + 6 = 214
|
40 videos|471 docs|57 tests
|
FAQs on NCERT Exemplar Solutions: Number System - Mathematics (Maths) Class 9
| 1. What is the importance of the Number System in mathematics? |  |
| 2. How does the Number System help in real-life applications? |  |
| 3. What are the different types of numbers in the Number System? |  |
| 4. How can the Number System be used to solve complex mathematical problems? |  |
| 5. Can you provide a real-life example where the Number System is used extensively? |  |