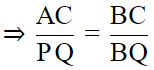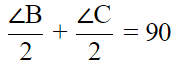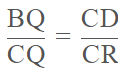NCERT Exemplar Solutions: Quadrilaterals | Mathematics (Maths) Class 9 PDF Download
| Table of contents |

|
| Exercise 8.1 |

|
| Exercise 8.2 |

|
| Exercise 8.3 |

|
| Exercise 8.4 |

|
Exercise 8.1
Write the correct answer in each of the following:
Q.1. Three angles of a quadrilateral are 75º, 90º and 75º. The fourth angle is
(a) 90º
(b) 95º
(c) 105º
(d) 120º
The correct answer is Option (d).
According to the question,
Three angles of quadrilateral are 75°, 90° and 75°
Consider the fourth angle to be x.
We know that,
Sum of all angles of a quadrilateral = 360°
⇒ 75° + 90° + 75° + x = 360°
⇒ 240° + x = 360°
⇒ x = 360° – 240°
⇒ x = 120°
Hence, the fourth angle is 120°.
Therefore, option (d) is the correct answer.
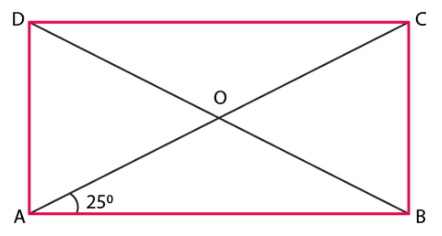
Q.2. A diagonal of a rectangle is inclined to one side of the rectangle at 25º. The acute angle between the diagonals is
(a) 55º
(b) 50º
(c) 40º
(d) 25º
The correct answer is Option (b).
According to the question,A diagonal of a rectangle is inclined to one side of the rectangle at 25º
i.e., the Angle between a side of a rectangle and its diagonal = 25°
Consider the acute angle between diagonals to be = x
We know that diagonals of a rectangle are equal in length i.e., AC = BD
Dividing RHS and LHS by 2,
⇒ ½ AC = ½ BD
Since, O is mid-point of AC and BD
⇒ OD = OC
Since, angles opposite to equal sides are equal
⇒ ∠y = 25°
We also know that,
Exterior angle is equal to the sum of two opposite interior angles.
So, ∠BOC = ∠ODC + ∠OCD
⇒ ∠x = ∠y + 25°
⇒ ∠x = 25° + 25°
⇒ ∠x = 50°Hence, the acute angle between diagonals is 50°.
Therefore, option (b) is the correct answer.
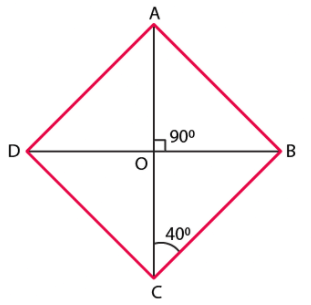
Q.3. ABCD is a rhombus such that ∠ACB = 40º. Then ∠ADB is
(a) 40º
(b) 45º
(c) 50º
(d) 60º
The correct answer is Option (c).
According to the question,
ABCD is a rhombus
∠ACB = 40°
∵ ∠ACB = 40°
⇒ ∠OCB = 40°
∵ AD ∥ BC
⇒ ∠DAC = ∠BCA = 40° [Alternate interior angles]
⇒ ∠DAO = 40°
Since the diagonals of a rhombus are perpendicular to each other
We have,
∠AOD = 90°
We know that, Sum of all angles of a triangle = 180°
⇒ ∠AOD + ∠ADO + ∠DAO = 180°
⇒ 90° + ∠ADO + 40° = 180°
⇒ 130° + ∠ADO = 180°
⇒ ∠ADO = 180° – 130°
⇒ ∠ADO = 50°
⇒ ∠ADB = 50°
Hence, ∠ADB = 50°
Therefore, option (c) is the correct answer.
Q.4. The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rectangle, if
(a) PQRS is a rectangle
(b) PQRS is a parallelogram
(c) diagonals of PQRS are perpendicular
(d) diagonals of PQRS are equal.
The correct answer is Option (c).
Let the rectangle be ABCD,
We know that the diagonals of a rectangle are equal
∴ AC = BD
⇒ PQ = QR
∴ PQRS is a rhombus
The diagonals of a rhombus are perpendicular.
Hence, the diagonals of PQRS are perpendicular.
Therefore, option (c) is the correct answer.
Q.5. The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rhombus, if
(a) PQRS is a rhombus
(b) PQRS is a parallelogram
(c) diagonals of PQRS are perpendicular
(d) diagonals of PQRS are equal.
The correct answer is Option (d).
Since ABCD is a rhombus
We have,
AB = BC = CD = DA
Now,
Since D and C are midpoints of PQ and PS
By the midpoint theorem,
We have,
DC = ½ QS
Also,
Since B and C are midpoints of SR and PS
By midpoint theorem
We have,
BC = ½ PR
Now, again, ABCD is a rhombus
∴ BC = CD
⇒ ½ QS = ½ PR
⇒ QS = PR
Hence, diagonals of PQRS are equal.
Therefore, option (d) is the correct answer.
Q.6. If angles A, B, C and D of the quadrilateral ABCD, taken in order, are in the ratio 3:7:6:4, then ABCD is a
(a) rhombus
(b) parallelogram
(c) trapezium
(d) kite
The correct answer is Option (c).
As angles A, B, C and D of the quadrilateral ABCD, taken in order, are in the ratio 3: 7: 6: 4,
We have the angles A, B, C and D = 3x, 7x, 6x and 4x.
Now, the sum of the angle of a quadrilateral = 360o.
3x + 7x + 6x + 4x = 360o
⇒ 20x = 360o
⇒ x = 360 ÷ 20 =18o
So, the angles A, B, C and D of quadrilateral ABCD are,
∠A = 3×18o = 54o,
∠B = 7×18o = 126o
∠C = 6×18o = 108o
∠D = 4×18o = 72o
AD and BC are two lines cut by a transversal CD
Now, the sum of angles ∠C and ∠D on the same side of the transversal,
∠C +∠D =108o + 72o =180
Hence, AD|| BC
So, ABCD is a quadrilateral in which one pair of opposite sides are parallel.
Hence, ABCD is a trapezium.
Therefore, option (c) is the correct answer.
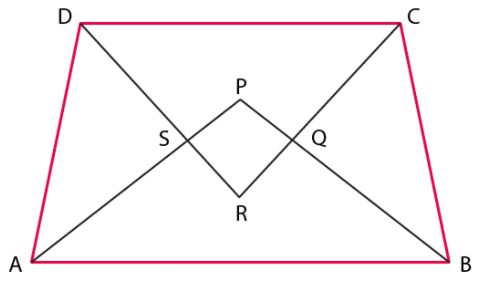
Q.7. If bisectors of ∠A and ∠B of a quadrilateral ABCD intersect each other at P, of ∠B and ∠C at Q, of ∠C and ∠D at R and of ∠D and ∠A at S, then PQRS is a
(a) rectangle
(b) rhombus
(c) parallelogram
(d) quadrilateral whose opposite angles are supplementary
The correct answer is Option (d).
We know that,
The sum of all angles of a quadrilateral = 360°
⇒ ∠A + ∠B + ∠C + ∠D = 360°
Dividing LHS and RHS by 2,
⇒ ½ (∠A + ∠B + ∠C + ∠D) = ½ × 360° = 180°
Since, AP, PB, RC and RD are bisectors of ∠A, ∠B, ∠C and ∠D
⇒ ∠PAB + ∠ABP + ∠RCD + ∠RDC = 180° … (1)
We also know that,
Sum of all angles of a triangle = 180°
∠PAB + ∠APB + ∠ABP = 180°
⇒ ∠PAB + ∠ABP = 180° – ∠APB …(2)
Similarly,
∴ ∠RDC + ∠RCD + ∠CRD = 180°
⇒ ∠RDC + ∠RCD = 180° – ∠CRD …(3)
Substituting the value of equations (2) and (3) in equation (1),
180° – ∠APB + 180° – ∠CRD = 180°
⇒ 360° – ∠APB – ∠CRD = 180°
⇒ ∠APB + ∠CRD = 360° – 180°
⇒ ∠APB + ∠CRD = 180° …(4)
Now,
∠SPQ = ∠APB [vertically opposite angles]
∠SRQ = ∠DRC [vertically opposite angles]
Substituting in equation (4),
⇒ ∠SPQ + ∠SRQ = 180°
Hence, PQRS is a quadrilateral whose opposite angles are supplementary.
Therefore, option (d) is the correct answer.
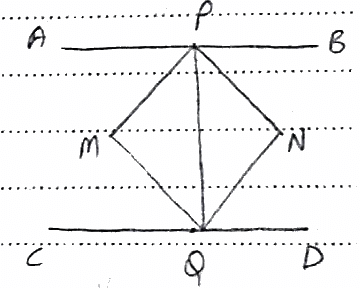
Q.8. If APB and CQD are two parallel lines, then the bisectors of the angles APQ, BPQ, CQP and PQD form
(a) a square
(b) a rhombus
(c) a rectangle
(d) any other parallelogram
The correct answer is Option (c).
APB and CQD are two parallel lines.
Let the bisector of angles APQ and CQP meet at point M and of BPQ and PQD at N.
Join PM, MQ,QN and NP.
APB∥CQD then,
∠APQ = ∠PQD [alternate interior angles]
2∠MPQ = 2∠NQP [PM and NQ are the angle bisectors of ∠APQ and ∠DQP respectively]
∠MPQ = ∠NQP; Therefore PM∥QN, because alternate interior angles are equal.
Similarly, ∠BPQ = ∠CQP [alternate interior angles]
Therefore PN∥QM
Hence, PMQN is a parallelogram.
∠CQD = 180
[∵ CQD is a line]
∠CQP+∠DQP = 180°2∠MQP+2∠NQP = 180° [MQ and NQ are bisectors of ∠CQP and ∠DQP]
∠MQP+∠NQP = 90°∠MQN = 90°
Hence, ∠MQN is a rectangle.
Q.9. The figure obtained by joining the mid-points of the sides of a rhombus, taken in order, is
(a) a rhombus
(b) a rectangle
(c) a square
(d) any parallelogram
The correct answer is Option (b).
Let ABCD be any rhombus and P, Q, R, S be the mid points of AB,BC,CD and DA respectively. Then we know that by the property of rhombus that AC ∥ PQ.
Observing △ACB and △PQB
∠ABC = ∠PBQ(same angles)
∠BAC = ∠BPQ(corresponding angles)
∠BCA = ∠BQP(corresponding angles)
△ABC is similer to △PBQ
⇒ PQ = (1/2)AC
Similarly taking △BCD and △RCQ
RQ = (1/2)BD
Then again △ADC and △SDR
SR = (1/2)AC
And at last
SP = (1/2)BD
∴ PQ = SR and RQ = SP
Opposite sides are equal.
Now,
∠APS + ∠SPQ + ∠BPQ = 180°
⇒ ∠ABD + ∠SPQ + ∠BAC = 180°
⇒ (1/2) (∠ABC) + ∠SPQ + (1/2)(∠BAD) = 180°
⇒ ∠SPQ + (1/2) (∠ABC+∠BAD) = 180°
By properties of rhombus
⇒ ∠SPQ + (1/2)(180°) = 180°
⇒ ∠SPQ = 90°
Similarly, ∠PQR = ∠QRS = ∠RSP = 90°
Thus, all angles measure 90° and opposite sides are equal.
Hence, the figure obtained is a rectangle.
Q.10. D and E are the mid-points of the sides AB and AC of ∆ABC and O is any point on side BC. O is joined to A. If P and Q are the mid-points of OB and OC respectively, then DEQP is
(a) a square
(b) a rectangle
(c) a rhombus
(d) a parallelogram
The correct answer is Option (d).
Given:
ABC is a triangle, D & E are the respective midpoints of AB & AC.
O is any point on BC, P & Q are midpoints of OB & OC respectively.
To find:
Type of quadrilateral of DEQP.
Solution:
In ΔABC, D & E are the respective midpoints of AB & AC.
∴DE ∥ (BC or PQ) ...(1)
Again, in ΔABO, P&D are the respective midpoints of AB & BO
∴DP ∥ AO ... (2)
Similarly, in ΔACO, EQ ∥ AO ...(3)
∴ From (2) & (3), we get
DP ∥ EQ ... (4)
∴ From (1) & (4), we have
DE ∥ PQ and DP ∥ EQ
So, DEQP is parallelogram.
Hence, option D is the correct answer,
Q.11. The figure formed by joining the mid-points of the sides of a quadrilateral ABCD, taken in order, is a square only if,
(a) ABCD is a rhombus
(b) diagonals of ABCD are equal
(c) diagonals of ABCD are equal and perpendicular
(d) diagonals of ABCD are perpendicular.
The correct answer is Option (c).
In given figure,
ABCD is a quadrilateral and P,Q,R & S are mid-pints of sides AB,BC,CD and DA respectively. Then, PQRS is a square.
∴ PQ = QR = RS = PS ...(1)
and PR = SQ
But PR = BC and SQ = AB
∴ AB = BC
Thus, all sides of quadrilateral ABCD are equal.
Hence, quadrilateral ABCD is either a square or a rhombus.
Now, in △ADB,
By using Mid-point theorem,
SP ∣∣ DB; SP = (1/2)DB ...(2)
Similarly in △ABC,
PQ || AC; PQ = (1/2)AC ...(3)
From equation (1),
PS = PQ
From (2) and (3),
(1/2)DB = (1/2)AC
∴ DB = AC
Thus, the diagonals of ABCD are equal, confirming that quadrilateral ABCD is a square. Therefore, the diagonals of the quadrilateral are also perpendicular.
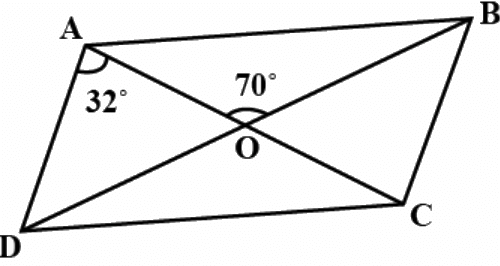
Q.12. The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC = 32º and ∠AOB = 70º, then ∠DBC is equal to
(a) 24º
(b) 86º
(c) 38º
(d) 32º
The correct answer is Option (c).
In the given figure,
Quadrilateral ABCD is a parallelogram.
So, AD ∣∣ BC
∴ ∠DAC = ∠ACB ...(Alternate angle)
∴ ∠ACB = 32°
∠AOB + ∠BOC = 180° ...(straight angle)
⇒70° + ∠BOC = 180°
∴ ∠BOC = 110°
In △BOC,
∠OBC + ∠BOC + ∠OCB = 180°
⇒∠OBC + 110° + 32° = 180°
⇒ ∠OBC = 38°
∴ ∠DBC = 38°
Q.13. Which of the following is not true for a parallelogram?
(a) opposite sides are equal
(b) opposite angles are equal
(c) opposite angles are bisected by the diagonals
(d) diagonals bisect each other.
The correct answer is Option (c).
Opposite angles are bisected by the diagonals
The four most important properties of a parallelogram are:
- The opposite sides of a parallelogram are equal in measurement and they are parallel to each other.
- The opposite angles of a parallelogram are equal.
- The sum of the interior angles of a parallelogram is equal to 360°.
- The consecutive angles of a parallelogram should be supplementary 180°.
Thus, opposite angles are bisected by the diagonals is not a property of a parallelogram.
Hence, option (c) is correct.
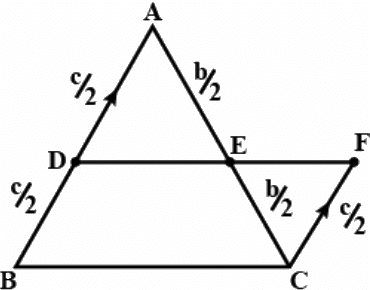
Q.14. D and E are the mid-points of the sides AB and AC respectively of ∆ABC. DE is produced to F. To prove that CF is equal and parallel to DA, we need an additional information which is
(a) ∠DAE = ∠EFC
(b) AE = EF
(c) DE = EF
(d) ∠ADE = ∠ECF.
The correct answer is Option (c).
Given CF is equal and parallel to DA
D is the midpoint of AB
So, AD = DB = CF = (c/2)
Similarly AE = EC = (b/2)
Let ∠AED = α ADE = β and DAE = γSince AD is parallel to FC
∠FEC = α ∠EFC = β and ∠ECF = γ
Applying S.A.S Congruency for triangle ADE and CFE, AD = CF, AE = AC
∠DAE = ∠ECF
So Δk DAE andΔk FCE are congruentSo DE = EF
It is given that DE = EF, then by S.S.S. congruency all angles will be equal and CF and parallel to DA
∴ Additional information needed is DE = EF.
Exercise 8.2
Q.1. Diagonals AC and BD of a parallelogram ABCD intersect each other at O. If OA = 3 cm and OD = 2 cm, determine the lengths of AC and BD.
According to the question,
OA = 3 cm
OD = 2 cm
We know that,
Diagonals of parallelogram bisect each other.
Then,
AC = 2AO
AC = 2 × 3 cm
AC = 6 cm
And,BD = 2OD
BD = 2 × 2 cm
BD = 4 cm
Hence, AC = 6 cm and BD = 4cm
Q.2. Diagonals of a parallelogram are perpendicular to each other. Is this statement true? Give reason for your answer.
The statement “diagonals of a parallelogram are perpendicular to each other” is false.
Justification:
Diagonals of a parallelogram bisect each other but not at 90°.
So, they are not perpendicular to each other.
Hence, this statement is false.
Q.3. Can the angles 110º, 80º, 70º and 95º be the angles of a quadrilateral? Why or why not?
The angles 110º, 80º, 70º and 95º cannot be the angles of a quadrilateral.
Justification:
We know that,
Sum of all angles of a quadrilateral = 360°
Sum of given angles,
110° + 80° + 70° + 95° = 355° ≠ 360°
Hence, 110°, 80°, 70° and 95° cannot be the angles of a quadrilateral.
Q.4. In quadrilateral ABCD, ∠A + ∠D = 180º. What special name can be given to this quadrilateral?
According to the question,
In quadrilateral ABCD, ∠A + ∠D = 180º
We know that,
In a trapezium,
Sum of co-interior angles = 180°
Hence, the given quadrilateral is a trapezium.
Q.5. All the angles of a quadrilateral are equal. What special name is given to this quadrilateral?
According to the question,
All the angles of a quadrilateral are equal.
Suppose all the angles of the quadrilateral = x
We know that,
Sum of all angles of a quadrilateral = 360°⇒ x + x + x + x = 360°
⇒ 4x = 360°
⇒ x = 360°/4
⇒ x = 90°
Hence, the quadrilateral is a rectangle.
Q.6. Diagonals of a rectangle are equal and perpendicular. Is this statement true? Give reason for your answer.
The statement “diagonals of a rectangle are equal and perpendicular” is false.
We know that,
Diagonals of a rectangle bisect each other.
Therefore, they are equal but they are not perpendicular.
Hence, the statement is not true.
Q.7. Can all the four angles of a quadrilateral be obtuse angles? Give reason for your answer.
All the four angles of a quadrilateral cannot be obtuse angles.
Justification:
We know that,
Sum of all angles of a quadrilateral = 360°
So, at least one angle should be acute angle.
Hence, all the four angles of a quadrilateral cannot be obtuse angles.
Q.8. In ∆ABC, AB = 5 cm, BC = 8 cm and CA = 7 cm. If D and E are respectively the mid-points of AB and BC, determine the length of DE.
Mid-Point Theorem :
The line segment joining the mid-points of two sides of a triangle is parallel to the third side and equal to half the third side.
On applying the midpoint theorem, we get
DE = AC/2 = 7/2 = 3.5cm
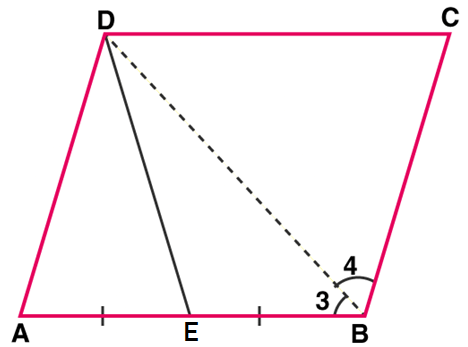
Q.9. In Fig.8.1, it is given that BDEF and FDCE are parallelograms. Can you say that BD = CD? Why or why not?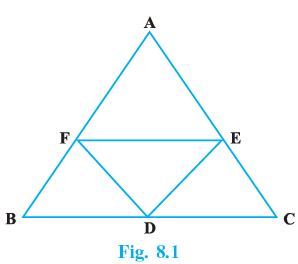
Given:-
ABC is a triangle. D,EF are points on BC,CA.AB taken in order. BDEF anf FDCE are parallelograms.
To Prove:-
BD = CD
Proof:-
In parallelogram BDEF,
BD = EF…(i) [Opposite sides of a parallelogram are equal.]
In parallelogram FDCE,
CD = EF …(ii) [Opposite sides of a parallelogram are equal.]
From (i) and (ii),
BD = CD
Hence proved.
Q.10. In Fig.8.2, ABCD and AEFG are two parallelograms. If ∠C = 55º, determine ∠F.
ABCD and AEFG are two parallelograms sharing two sides AD (or AG) and AE (or AE) and the included angle.
∠C = 55°.
To find out: ∠F
Solution-
We have ∠F = ∠A ...(opposite angles of a parallelogram) ...(i)
Again ∠A = ∠C ...(opposite angles of a parallelogram) ...(ii)
∴∠F = ∠C ...[From (i) and (ii)]
And ∠C=55° ...(given)
⇒ ∠F = 55°
Q.11. Can all the angles of a quadrilateral be acute angles? Give reason for your answer.
We know that an acute angle is less than 90°. All the angles of a quadrilateral cannot be acute angles because than the sum of angles of quadrilateral will be less than 360°, whereas angle sum of quadrilateral is 360°. Therefore, it is impossible for all angles to be acute.
Q.12. Can all the angles of a quadrilateral be right angles? Give reason for your answer.
Yes, all the angles of a quadrilateral can indeed be right angles. The sum of the angles in a quadrilateral is 360°. If each angle measures 90°, then: 90° + 90° + 90° + 90° = 360°. This confirms that it is possible for all angles in a quadrilateral to be right angles.
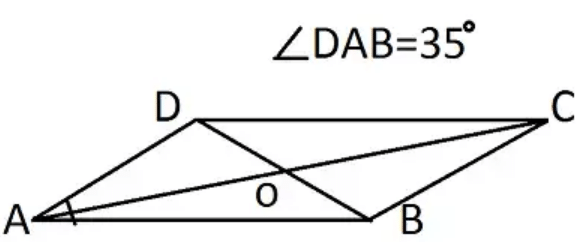
Q.13. Diagonals of a quadrilateral ABCD bisect each other. If ∠A = 35º, determine ∠B.
Given: ABCD is a quadrilateral with AC & BD as its diagonals bisecting each other at O. ∠BAD=35°.
To find out: m ∠ ABC
Solution-
Between ΔAOD & ΔBOC we have,AO = CO & DO = BO ...(since AC & BD bisect each other at O)
∠AOD = ∠BOC
∴ΔAOD & ΔBOC are congruent. ⇒ AD ∥ BC
Now, AB is the transversal to AD & BC$$
So, ∠BAD + ∠ABD = 180° ...(same side internal angles)
⇒ 35° + ∠ABD = 180°⇒ ∠ABD = 145°
∠B = 145°
Q.14. Opposite angles of a quadrilateral A BC D are equal. If AB = 4 cm, determine CD.
Let ABCD be a quadrilateral.
Given, opposite angles of a quadrilateral ABCD are equal.
So, opposite sides of the quadrilateral ABCD are equal.
⇒ AB = CD
Given, AB = 4 cm
Therefore, CD = 4 cm.
Exercise 8.3
Q.1. One angle of a quadrilateral is of 108º and the remaining three angles are equal. Find each of the three equal angles.
Let the remaining three equal angles be x.
We know,
Sum of all interior angles of a quadrilateral is = 360o
108o + x + x + x = 360o
108o + 3x = 360o
3x = 360o – 108o
3x = 252o
x = 252/3
x = 84o
Each of three equal angles, x = 84o.
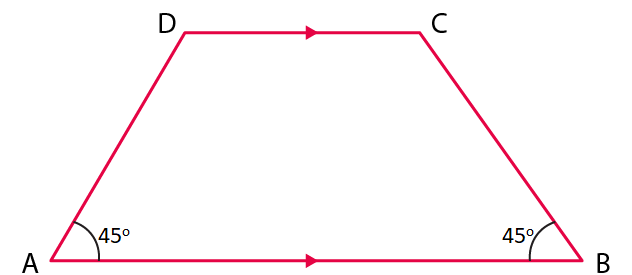
Q.2. ABCD is a trapezium in which AB || DC and ∠A = ∠B = 45º. Find angles C and D of the trapezium.
According to the question,
ABCD is a trapezium
∠A = ∠B = 45º
We know that,
Angles opposite to each other in quadrilateral are supplementary.
Then, we have,
∠A+ ∠C = 180º
45º + ∠C = 180º
∠C = 180º – 45º
∠C = 135º
Similarly,
We have,
∠B + ∠D = 180º
45º + ∠D = 180º
∠D = 180º – 45º
∠D = 135º
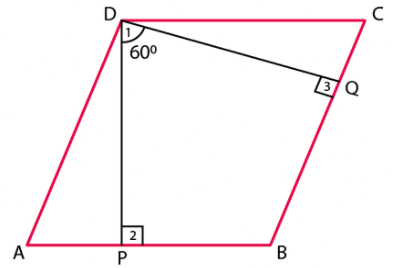
Q.3. The angle between two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 60º. Find the angles of the parallelogram.
According to the question,
ABCD is parallelogram,
DP ⊥ AB
DQ ⊥ BC.
∠PDQ = 60º
In quad. DPBQ, Using angle sum property of a quadrilateral,
We have,
∠PDQ + ∠Q + ∠P + ∠B = 360º
60º + 90º + 90º + ∠B = 360º
240º + ∠B = 360º
∠B = 360º – 240º
∠B = 120º
Since, opposite angles in parallelogram are equal,
We have,
∠B = ∠D = 120º
Since, opposite sides are parallel in parallelogram,
We have,
AB||CD
Also, since sum of adjacent interior angles is 180o,
We have,
∠B + ∠C = 180º
120º + ∠C = 180º
∠C = 180º – 120º
∠C = 60º
Since, opposite angles in parallelogram are equal,
We have,
∠C = ∠A = 60º
Q.4. ABCD is a rhombus in which altitude from D to side AB bisects AB. Find the angles of the rhombus.
According to the question,
We have,
ABCD is a rhombus.
DE is the altitude on AB then AE = EB.
In ΔAED and ΔBED,
We have,
DE = DE (common line)
∠AED = ∠BED (right angle)
AE = EB (DE is an altitude)
∴ ΔAED ≅ ΔBED by SAS property.
∴ AD = BD (by C.P.C.T)
But AD = AB (sides of a rhombus are equal)
⇒ AD = AB = BD∴ ABD is an equilateral triangle.
∴ ∠A = 60º
Since opposite angles of the rhombus are equal, we get,
⇒ ∠A = ∠C = 60º
We also know that,
The sum of adjacent angles of a rhombus = supplementary.
So,
∠ABC + ∠BCD = 180º
∠ABC + 60º = 180º
∠ABC = 180º – 60º= 120º
Since opposite angles of a rhombus are equal, we get,
∠ABC = ∠ADC = 120o
Hence, the angles of the rhombus are:
∠A = 60º, ∠C = 60º, ∠B = 120º, ∠D = 120º
Q.5. E and F are points on diagonal AC of a parallelogram ABCD such that AE = CF. Show that BFDE is a parallelogram.
Construction:
Join BD, meeting AC at O.
According to the question,
Since diagonals of a parallelogram bisect each other,
We get,
OA = OC and OD = OB.
And,
OA = OC and AE = CF,
OA – AE = OC – CF
OE = OF
So, BFDE is a quadrilateral whose diagonals bisect each other.
Hence, BFDE is a parallelogram.
Q.6. E is the mid-point of the side AD of the trapezium ABCD with AB || DC. A line through E drawn parallel to AB intersect BC at F. Show that F is the mid-point of BC. [Hint: Join AC]
ABCD is a trapezium in which AB ∥ DC, BD is a diagonal and E is the mid-point of AD and a line drawn through E parallel to AB intersecting BC at F such that EF ∥ AB.
⇒ Let EF intersected BD at G.
In △ABD,
E is the mid-point of AD and also EG ∥ AB.
We get, G is the mid-point of BD [ By converse of mid-point theorem ]
Similarly,
In △BDC,
G is mid-point of BD and GF ∥ AB ∥ DC.
∴ F is the mid-point of BC [By converse of midpoint theorem]
Q.7. Through A, B and C, lines RQ, PR and QP have been drawn, respectively parallel to sides BC, CA and AB of a ∆ ABC as shown in Fig.8.5. Show that BC = (1/2)QR.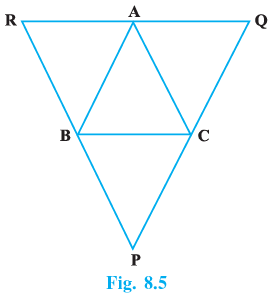
Given: Triangle ABC and PQR in which AB ∣∣ PQ, BC ∣∣ RQ and CA ∣∣ PR
To prove: BC = (1/2)QR
Proof: Quadrilatral RBCA is a parallelogram.
(∵RA ∣∣ BC and BR ∣∣ CA)
∴RA = BC ...(1) (∵ Opposite side of parallelogram)
Now, quadrilateral BCQA is a parallelogram.
∴ AQ = BC ...(2)(∵ Opposite side of parallelogram)
Adding (1) and (2), we get,
⇒ RA + AQ = 2BC
⇒ QR = 2BC
⇒ BC = (1/2)QR
Hence proved.
Q.8. D, E and F are the mid-points of the sides BC, CA a n d AB, respectively of an equilateral triangle ABC. Show that ∆ DEF is also an equilateral triangle.
Let ABC be the triangle and D, E and F be the mid-point of BC, CA and AB respectively. We have to show triangle formed DEF is an equilateral triangle. We know the line segment joining the mid-points of two sides of a triangle is half of the third side.
Therefore DE = (1/2)AB, EF = (1/2) BC and FD = (1/2)AC
Now, ΔABC is an equilateral triangle
⇒ AB = BC = CA
⇒ (1/2)AB = (1/2)BC = (1/2)CA
⇒ DE = EF = FD
∴ ΔDEF is an equilateral triangle.
Q.9. Points P and Q have been taken on opposite sides AB and CD, respectively of a parallelogram ABCD such that AP = CQ (Fig. 8.6). Show that AC and PQ bisect each other.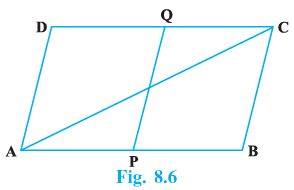
In △APO and △OQC
∠OAP = ∠OCQ ( taking AC as transversal then angles are on opposites sides of transversal)
AP = CQ (given )
∠OPA = ∠OQC ( taking PQ as transversal then angles are on opposites sides of transversal )
By ASA criterion of congruency ,△APO is congruent to △OQC.
PO = OQ, AO = OC ( Corresponding parts of a congruent triangle are equal )
Hence AC and PQ bisect each other.
Q.10. In Fig. 8.7, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP = ∠DAP. Prove that AD = 2CD.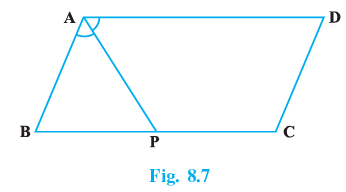
In given figure,
∠BPA = ∠DAP
Because AP is a line which intersect two parallel line AD and BC
So, According given data
∠BAP = ∠BAP
∠BPA = ∠BAP
So, AB = BP
and AB ∣∣ CD
So, AD = BC
and P is mid point of BC
So, 2BP = BC
2BP = AD
AD = 2AB
AB = CD
AD = 2CD
Hence proved.
Exercise 8.4
Q.1. A square is inscribed in an isosceles right triangle so that the square and the triangle have one angle common. Show that the vertex of the square opposite the vertex of the common angle bisects the hypotenuse.
According to the question,
ΔABC with ∠A = 90o and
Since, ABC is an isosceles triangle,
We get,
AB = AC …(i)
Let ADEF be the square inscribed in the isosceles triangle ABC. Then, we have,
AD = AF = EF = AD …(ii)
Subtracting equation (ii) from (i),
AB – AD = AC – AF
BD = CF
Now,
Considering ΔCFE and ΔEDB,
BD = CF
DE = EF
∠CFE = ∠EDB = 90o (Since they are the side of a square)
ΔCEF ~ ΔBED (By SAS criteria)
Hence, CE = BE
Therefore, vertex E of the square bisects the hypotenuse BC.
Q.2. In a parallelogram ABCD, AB = 10 cm and AD = 6 cm. The bisector of ∠A meets DC in E. AE and BC produced meet at F. Find the length of CF.
According to the question,
We have,
ABCD is a parallelogram
AB = 10 cm
AD = 6cm.
The bisector of ∠A meets DC at E.
AE and BC produced meet at F.
Since, AF bisects ∠A,
We get,
∠BAE = ∠EAD … (1)
∠EAD = ∠EFB … (2) [Alternate angles]
From equations (1) and (2),
We get,
∠BAE = ∠EFB
Since sides opposite to equal angles are equal,
We get,
BF = AB
Here, AB = 10 cm
So, BF = 10 cm
⇒ BC + CF = 10 cm
6 cm + CF = 10 cm [BC = AD = 6 cm, opposite sides of a parallelogram]
⇒ CF = 10 – 6 cm = 4 cm
⇒ CF = 4 cm
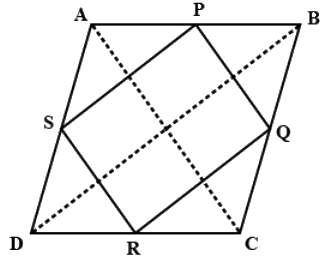
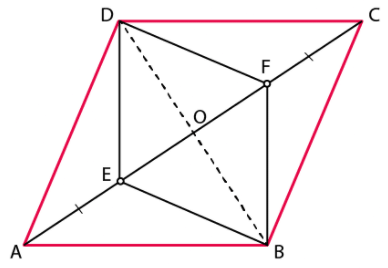
Q.3. P, Q, R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
According to the question,
We have,
P is the mid-point of the sides AB
Q is the mid-point of the sides BC
R is the mid-point of the sides CD
S is the mid-point of the sides DA
Also, we know that,
AC = BD.
In ΔADC, by mid-point theorem,
SR = ½ AC
And, SR||AC
In ΔABC, by mid-point theorem,
PQ = ½ AC
And, PQ||AC
Hence, SR = PQ = ½ AC
Similarly,
In ΔBCD, by mid-point theorem,
RQ = ½ BD
And, RQ||BD
In ΔBAD, by mid-point theorem,
SP = ½ BD
And, SP||BD
So, we get,
SP = RQ = ½ BD = ½ AC
Then,
SR = PQ = SP = RQ
Hence, PQRS is a rhombus.
Q.4. P, Q, R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD such that AC ⊥ BD. Prove that PQRS is a rectangle.
According to the question,
We have,
P is the mid-point of the sides AB
Q is the mid-point of the sides BC
R is the mid-point of the sides CD
S is the mid-point of the sides DA
Also,
AC ⊥ BD
∠COD = ∠AOD = ∠AOB = ∠COB = 90o
In ΔADC, by mid-point theorem,
SR = ½ AC
And, SR||AC
In ΔABC, by mid-point theorem,
PQ = ½ AC
And, PQ||AC
So, we have,
PQ||SR and SR = PQ = ½ AC
Similarly,
SP||RQ and SP = RQ = ½ BD
Now, in quadrilateral EOFR,
OE||FR and OF||ER
So, we get,
∠EOF = ∠ERF = 90o
Hence, PQRS is a rectangle.
Q.5. P, Q, R and S are respectively the mid-points of sides AB, BC, CD and DA of quadrilateral ABCD in which AC = BD and AC ⊥ BD. Prove that PQRS is a square.
According to the question,
We have,
P is the mid-point of the sides AB
Q is the mid-point of the sides BC
R is the mid-point of the sides CD
S is the mid-point of the sides DA
Also,
AC ⊥ BD
And AC = BD
In ΔADC, by mid-point theorem,
SR = ½ AC
And, SR||AC
In ΔABC, by mid-point theorem,
PQ = ½ AC
And, PQ||AC
So, we have,
PQ||SR and PQ = SR = ½ AC
Now, in ΔABD, by mid-point theorem,
SP||BD and SP = ½ BD = ½ AC
In ΔBCD, by mid-point theorem,
RQ||BD and RQ = ½ BD = ½ AC
SP = RQ = ½ AC
PQ = SR = SP = RQ
Thus, we get that,
All four sides are equal.
Considering the quadrilateral EOFR,
OE||FR, OF||ER
∠EOF = ∠ERF = 90o (Opposite angles of parallelogram)
∠QRS = 90o
Hence, PQRS is a square.
Q.6. A diagonal of a parallelogram bisects one of its angles. Show that it is a rhombus.
Let the parallelogram be = ABCD
Diagonal AC bisect ∠A.
∠CAB = ∠CAD
Now,
AB||CD and AC is a transversal.
∠CAB = ∠ACD
Again, AD||BC and AC is a transversal.
∠DAC = ∠ACB
Now,
∠A = ∠C
½ ∠A = ½ ∠C
∠DAC = ∠DCA
AD = CD
But, AB = CD and AD = BC (Opposite sides of parallelograms)
AB = BC = CD = AD
Thus, ABCD is a rhombus.
Q.7. P and Q are the mid-points of the opposite sides AB and CD of a parallelogram ABCD. AQ intersects DP at S and BQ intersects CP at R. Show that PRQS is a parallelogram.
According to the question,
Q is the midpoint of AB
P is the midpoint of CD
Now,
AB||CD,
Also,
AP||QC
And, AB = DC
½ AB = ½ DC
AP = QC
Now,
AP||QC and AP = QC
APCQ is a parallelogram.
AQ||PC or SQ||PR
Again,
AB||DC means ½ AB = ½ DC
BP = QD
Now, BP||QD and BP = QD
BPDQ is a parallelogram
So, PD||BQ or PS||QR
Thus, SQ||RP and PS||QR
PQRS is a parallelogram.
Q.8. ABCD is a quadrilateral in which AB || DC and AD = BC. Prove that ∠A = ∠B and ∠C = ∠D.
According to the question,
We have,
Quadrilateral ABCD
AB||CD and AD = BC.
To prove: ∠A = ∠B and ∠C = ∠D.
Construction: Draw DP ⊥ AB and CQ ⊥ AB.
Proof: In ΔAPD and ΔBQC,
Since ∠1 and ∠2 are equal to 90o
∠1 = ∠2
Distance between parallel line,
AB = BC [Given]
By RHS criterion of congruence,
We have
ΔAPD ≅ ΔBQC [CPCT]
∠A = ∠B
Now, DC||AB
Since, sum of consecutive interior angles is 180o
∠A+∠3 =180 …(1)
And,
∠B +∠4 =180 …(2)From equations (1) and (2),
We get
∠A + ∠3 = ∠B + ∠4
Since, ∠A = ∠B,
We have,⇒ ∠3 = ∠4
⇒ ∠C = ∠D
Hence, proved.
Q.9. In Fig. 8.11, AB || DE, AB = DE, AC || DF and AC = DF. Prove that BC || EF and BC = EF.
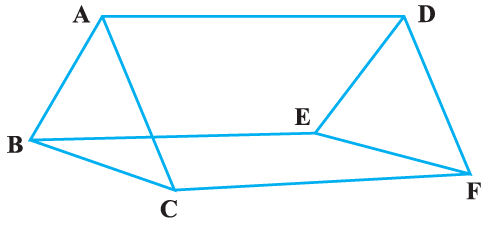
According to the question,
In quadrilateral ABED,
We have,
AB||DE and AB = DE
ABED is a parallelogram.
AD||BE and AD = BE
In quadrilateral ACFD,
We have,
AC||FD and AC = FD
ACFD is a parallelogram.
AD||CF and AD = CF
AD = BE = CF and CF||BE
In quadrilateral BCFE,
BE = CF and BE||CF.
BCFE is a parallelogram.
BC = EF and BC||EF
Hence proved.
Q.10. E is the mid-point of a median AD of ∆ABC and BE is produced to meet AC at F. Show that AF = (1/3)AC.
Given:-
AD is the median of ΔABC and E is the midpoint of AD
Through D draw DG∣∣BF
In ΔADG
E is the midpoint of AD and EF ∣∣ DG
By converse of midpoint theorem we have
F is midpoint of AG and AF = FG ...1
Similarly, in ΔBCF
D is the midpoint of BC and DG∣∣BF
G is midpoint of CF and FG = GC ...2
From equations 1 and 2
we will get
AF = FG = GC ...3
AF+ FG + GC= AC
AF + AF + AF = AC ... from eq 3
AF = AC
AF = (1/3)AC
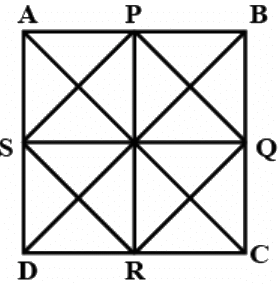
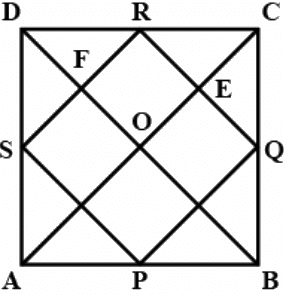
Q.11. Show that the quadrilateral formed by joining the mid-points of the consecutive sides of a square is also a square.
In a square ABCD, P, Q, R and S are the mid-points of AB, BC, CD and DA respectively.
⇒ AB = BC = CD = AD [Sides of square are equal]
In △ADC,
SR ∥ AC and SR = (1/2)AC [By mid-point theorem] ...(1)
In △ABC,
PQ ∥ AC and PQ = (1/2)AC [By mid-point theorem] ...(2)
From equation (1) and (2),
SR ∥ PQ and SR = PQ = (1/2)AC ...(3)
Similarly, SP ∥ BD and BD ∥ RQ
∴ SP ∥ RQ and SP = (1/2)BD and RQ = (1/2)BD
∴ SP = RQ = (1/2)BD
Since, diagonals of a square bisect each other at right angle.
∴ AC = BD
⇒ SP = RQ = (1/2)AC ...(4)
From (3) and (4)
SR = PQ= SP = RQ
We know that the diagonals of a square bisect each other at right angles.
∠EOF = 90°.
Now, RQ ∥ DB
RE ∥ FO
Also, SR ∥ AC
⇒ FR ∥ OE
∴ OERF is a parallelogram.
So, ∠FRE = ∠EOF = 90° (Opposite angles are equal)
Thus, PQRS is a parallelogram with ∠R = 90° and SR = PQ = SP = RQ
∴ PQRS is a square.
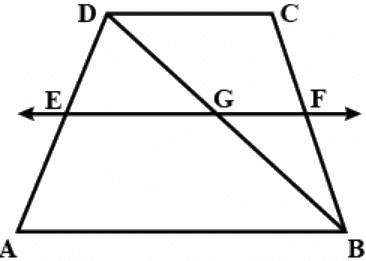
Q.12. E and F are respectively the mid-points of the non-parallel sides AD and BC of a trapezium ABCD. Prove that EF || AB and EF = (1/2)(AB + CD). [Hint: Join BE and produce it to meet CD produced at G.]
Given: A trapezium ABCD in which E and F are respectively the mid-points of the non-parallel sides AD and BC
To prove: EF ∣∣ AB and EF = (1/2) (AB + CD)
Construction: Join DF and produce it to intersect AB produced at G.
Proof: In ΔCFD and ΔBFG, we have
DC∣∣AB
∴ ∠C = ∠3 [Alternate interior angles]
CF = BF
∠1 = ∠2 [Vertically opposite angles]
So, by ASA criterion of congruence, we have
ΔCFD ≅ ΔBFG
∴ CD = BG(CPCT)
In ΔDAG, EF joins mid-points of sides AD and GD respectively
∴ EF ∣∣ AG [∵ Mid-point theorem]
⇒ EF ∣∣ AB
So, EF = (1/2)AG[ Mid-point theorem]
EF = (1/2) (AB + AG)
EF = (1/2)(AB + CD) [∵ CD = BG]
Hence proved.
Q.13. Prove that the quadrilateral formed by the bisectors of the angles of a parallelogram is a rectangle.
ABCD is a parallelogram
The adjacent angles of a parallelogram sum up to give 180°
i.e., ∠B + ∠C = 180°
From ΔOBC ⇒ ∠O = 90°
⇒ ∠POR = 90°
Similarly, all the 4 vetrices have right angles at their corners
Hence PQRS is rectangle.
Q.14. P and Q are points on opposite sides AD and BC of a parallelogram ABCD such that PQ passes through the point of intersection O of its diagonals AC and BD. Show that PQ is bisected at O.
ABCD is a parallelogram whose diagonals bisect each other at O.
In △ODP and △OBQ,
⇒ ∠BOQ = ∠POD [Vertically opposite angles are equal]
⇒ ∠OBQ = ∠ODP [ Alternate interior angles]
⇒ OB = OD [Given]
∴ △ODP ≅ △OBQ [By ASA congruence rule]
∴ OP = OQ [ By C.P.C.T ]
Hence, PQ is bisected at O.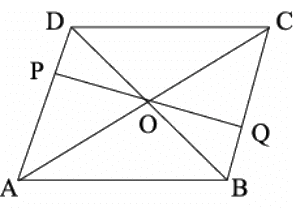
Q.15. ABCD is a rectangle in which diagonal BD bisects ∠B. Show that ABCD is a square.
In a rectangle ABCD, diagonal BD bisects ∠B.
Join AC.
In △BAD and △BCD,
⇒ ∠ABD = ∠CBD [ Since BD bisect ∠B ]
⇒ ∠A = ∠C [ Each angle of a rectangle is 90°. ]
⇒ BD = BD [ Common side ]
∴ △BAD ≅ △BCD [ By AAS congruence rule ]
⇒ AB = BC and AD = CD [CPCT] ...( 1 )
We know opposite sides of rectangle are equal.
∴ AB = CD and BC = AD ...( 2 )
From ( 1 ) and ( 2 ),
⇒ AB = BC = CD = DA
∴ ABCD is a square.
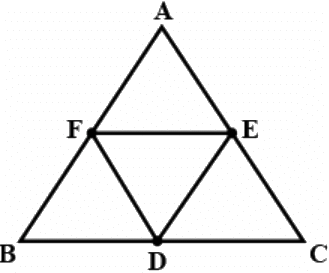
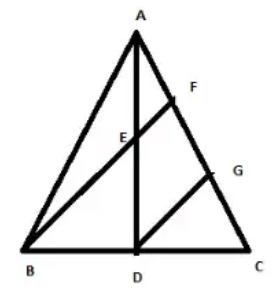
Q.16. D, E and F are respectively the mid-points of the sides AB, BC and CA of a triangle ABC. Prove that by joining these mid-points D, E and F, the triangles ABC is divided into four congruent triangles.
Given:
A ΔABC and ΔDEF which is formed by joining the mid-point D,E and F of the sides AB,BC and CA of ΔABC
Refer image,
To prove: ΔDEF ≅ ΔEDB ≅ ΔCFE ≅ ΔFAD
Proof: DF joins mid-points of sides AB and AC respectively of ΔABC
∴ DF ∣∣ BC [Mid-point theorem]
⇒ DF ∣∣ BE
SImilarly, EF ∣∣ BD
So, quadrilateral BEFD is a parallelogram.
⇒ ΔDEF ≅ ΔEDB.........(1)
(∵ DIagonal of parallelogram divides it into two congruent triangles)
Similarly, ΔDEF ≅ ΔCFE ...(2)
and ΔDEF ≅ ΔFAD ...(3)
From equation (1), (2) and (3), we get
ΔDEF ≅ ΔEDB ≅ ΔCFE ≅ ΔFAD
Hence proved.
Q.17. Prove that the line joining the mid-points of the diagonals of a trapezium is parallel to the parallel sides of the trapezium.
Let E and F are midpoints of the diagonals AC and BD of trapezium ABCD respectively.
Draw DE and produce it to meet AB at G
Consider △AEG and △CED
⇒ ∠AEG = ∠CED [Vertically opposite angles]
⇒ AE = EC [E is midpoint of AC]
⇒ ∠ECD = ∠EAG [ Alternate angles ]
⇒ △AEG ≅ △CED [ By SAA congruence rule ]
⇒ DE = EG ...(1) [CPCT]
⇒ AG = CD ... (2)
In △DGB
E is the midpoint of DG [ From ( 1 ) ]
F is midpoint of BD
∴ EF ∥ GB
⇒ EF ∥ AB [ Since GB is part of AB ]
⇒ EF is parallel to AB and CD.Also, EF= (1/2)GB
⇒ EF= (1/2) (AB-AG)
⇒ EF= (1/2)(AB - CD) [From ( 2 )]
Hence proved.
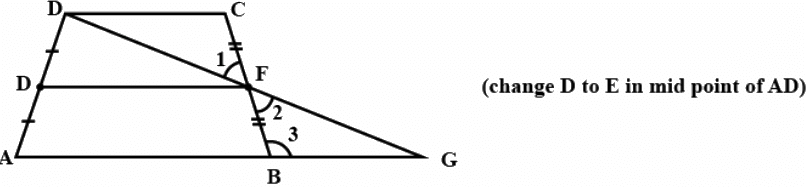
Q.18. P is the mid-point of the side CD of a parallelogram ABCD. A line through C parallel to PA intersects AB at Q and DA produced at R. Prove that DA = AR and CQ = QR.
Refer attached image, given ABCD is a parallelogram
AP∥CR
CP = PD
Since, △APD ∼ △RCD(AAA)(CPCT)
(As P is the mid point of CD)
⇒ 2DA = DR
⇒ 2DA = DA + AR
⇒ DA = AR
Hence Proved DA = AR
Again as, ∠APD = ∠QCD & ∠BQC = ∠APD(AP ∥ QC),
⇒ ∠APD = ∠QCD = ∠BQC & ∠RDC = ∠CBQ(Opposite of ∠ is ∥gm) & ∠BCQ = ∠CRD(Properties of ∥gm)
⇒ △BQC ∼ △DCR (AAA)
Now,
As,
⇒ △APD ≅ △CBQ
PD = BQ(As P is the midpoint of CD)
(In ∥gm AB = CD)
⇒ Q is the mid-point of AB
Again, as, △BQC ∼ △DCR
⇒ 2CQ = CR(As CD = 2BQ)
⇒ 2CQ = CQ + QR
⇒ CQ = QR
Hence proved.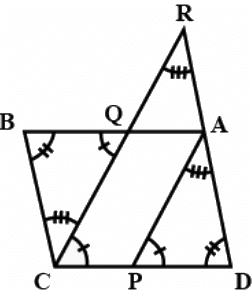
|
40 videos|471 docs|57 tests
|
FAQs on NCERT Exemplar Solutions: Quadrilaterals - Mathematics (Maths) Class 9
| 1. What are quadrilaterals and how are they classified ? |  |
| 2. What is the sum of the interior angles of a quadrilateral ? |  |
| 3. How can we prove that opposite angles of a parallelogram are equal ? |  |
| 4. What are the properties of a rectangle and how is it different from a square ? |  |
| 5. How can we find the area of different types of quadrilaterals ? |  |