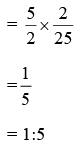NCERT Exemplar Solutions: अनुपात और अनुपात (Ratio & Proportion) | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download

व्यायाम पृष्ठ: 120

प्रश्न 1 से 10 तक, चार विकल्पों में से केवल एक सही है। सही विकल्प लिखें।

प्रश्न 1: 8 किताबों और 20 किताबों का अनुपात है (a) 2 : 5 (b) 5 : 2 (c) 4 : 5 (d) 5 : 4

उत्तर: (a) दो संख्याओं या मात्राओं की तुलना को विभाजन द्वारा किया जाता है, जिसे अनुपात कहा जाता है। अनुपात दर्शाने के लिए ‘:’ प्रतीक का उपयोग किया जाता है। 8 किताबों और 20 किताबों का अनुपात = 8/20 है। दोनों अंश और हर को 4 से विभाजित करें। = 2/5 इसलिए, 8 किताबों और 20 किताबों का अनुपात = 2 : 5

प्रश्न 2: एक वर्ग के भुजाओं की संख्या और एक घन के किनारों की संख्या का अनुपात है (a) 1 : 2 (b) 3 : 2 (c) 4 : 1 (d) 1 : 3

उत्तर: (d) हमें पता है कि, एक वर्ग में भुजाओं की संख्या = 4 और एक घन में किनारों की संख्या = 12 है। अतः, भुजाओं और किनारों का अनुपात = 4/12। दोनों अंश और हर को 4 से विभाजित करें। = 1/3 इसलिए, भुजाओं और किनारों का अनुपात = 1 : 3

प्रश्न 3: एक चित्र की चौड़ाई 60 सेमी और लंबाई 1.8 मीटर है। इसकी चौड़ाई और परिधि का अनुपात निम्नतम रूप में है (a) 1 : 2 (b) 1 : 3 (c) 1 : 4 (d) 1 : 8

उत्तर: (d) प्रश्न से दिया गया है कि, चित्र की चौड़ाई = 60 सेमी लंबाई = 1.8 मीटर है। हम जानते हैं कि, 1 मीटर = 100 सेमी, इसलिए 1.8 मीटर = 180 सेमी है। आयत की परिधि = 2 (लंबाई + चौड़ाई) = 2 (180 + 60) = 2 (240) = 480 है। इसलिए, इसकी चौड़ाई और परिधि का अनुपात निम्नतम रूप में = 60/480। दोनों अंश और हर को 20 से विभाजित करें। = 3/24 फिर, दोनों अंश और हर को 3 से विभाजित करें। = 1/8 = 1 : 8

प्रश्न 4: नीलम की वार्षिक आय ₹288000 है। उसकी वार्षिक बचत ₹36000 है। उसकी बचत और खर्च का अनुपात है (a) 1 : 8 (b) 1 : 7 (c) 1 : 6 (d) 1 : 5

उत्तर: (b) प्रश्न से यह दिया गया है कि, नीलम की वार्षिक आय ₹ 288000 है। उसकी वार्षिक बचत ₹ 36000 है। इसलिए, नीलम का व्यय = 288000 – 36000 = ₹ 252000। फिर, उसकी बचत और व्यय का अनुपात = 36000/252000 = 36/252। दोनों अंश और हर को 12 से विभाजित करें। = 3/21। फिर से, दोनों अंश और हर को 3 से विभाजित करें। = 1/7। इसलिए, उसकी बचत और व्यय का अनुपात = 1 : 7।

प्रश्न 5: कक्षा VI के लिए गणित की पाठ्यपुस्तक में 320 पृष्ठ हैं। अध्याय ‘साम्य’ पृष्ठ 261 से पृष्ठ 272 तक है। इस अध्याय के पृष्ठों की संख्या और पुस्तक के कुल पृष्ठों का अनुपात क्या है? (a) 11 : 320 (b) 3 : 40 (c) 3 : 80 (d) 272 : 320

उत्तर: (c) प्रश्न से यह दिया गया है कि, कक्षा VI के लिए गणित की पाठ्यपुस्तक में कुल पृष्ठ = 320 पृष्ठ। अध्याय ‘साम्य’ पृष्ठ 261 से पृष्ठ 272 तक है। साम्य अध्याय के पृष्ठों की संख्या = 12। इसलिए, साम्य अध्याय के पृष्ठों की संख्या और पुस्तक के कुल पृष्ठों का अनुपात है, = 12/320। दोनों अंश और हर को 2 से विभाजित करें। = 6/160। फिर से, दोनों अंश और हर को 2 से विभाजित करें। = 3/80। इसलिए, इस अध्याय के पृष्ठों की संख्या और पुस्तक के कुल पृष्ठों का अनुपात 3: 80 है।

प्रश्न 6: एक बॉक्स में, लाल गोले और नीले गोले का अनुपात 7:4 है। निम्नलिखित में से बॉक्स में कुल गोले की संख्या क्या हो सकती है? (a) 18 (b) 19 (c) 21 (d) 22

उत्तर: (d) प्रश्न से यह दिया गया है कि, लाल गोले और नीले गोले का अनुपात 7:4 है। अब, मान लेते हैं कि 7 और 4 का सामान्य गुणांक x है। इसलिए, बॉक्स में कुल गोले की संख्या = 7x + 4x = 11x। इसलिए, बॉक्स में गोले की संख्या 11 का गुणांक है। इसलिए, 11 × 2 = 22।

प्रश्न 7: एक शेल्फ पर, हरे कवर वाली किताबों और भूरे कवर वाली किताबों का अनुपात 2 : 3 है। यदि हरे कवर वाली किताबें 18 हैं, तो भूरे कवर वाली किताबों की संख्या है (क) 12 (ख) 24 (ग) 27 (घ) 36

उत्तर: (ग) प्रश्न से यह दिया गया है कि, एक शेल्फ पर, हरे कवर वाली किताबें और भूरे कवर वाली किताबें 2:3 के अनुपात में हैं। हरे कवर वाली किताबें 18 हैं। इसलिए, हम मान लेते हैं कि 2 और 3 का सामान्य गुणांक x है। तब, 2x = 18, x = 18/2। दोनों को 2 से विभाजित करने पर, x = 9। इसलिए, भूरे कवर वाली किताबों की संख्या = 3x = 3 × 9 = 27।

प्रश्न 8: अनुपात 2 : 3, 5 : 8, 75 : 121 और 40 : 25 में सबसे बड़ा अनुपात है (क) 2 : 3 (ख) 5 : 8 (ग) 75 : 121 (घ) 40 : 25

उत्तर: (घ) दिए गए अनुपातों पर विचार करें, 2 : 3, 5 : 8, 75 : 121 और 40 : 25। 2: 3 का सरलीकृत रूप = 2/3 = 0.67। 5 : 8 का सरलीकृत रूप = 5/8 = 0.625। 75: 121 का सरलीकृत रूप = 75/121 = 0.61। 40: 25 का सरलीकृत रूप = 40/25 = 1.6। इसलिए, दिए गए अनुपातों में सबसे बड़ा अनुपात 40 : 25 है।

प्रश्न 9: एक कक्षा में ‘b’ लड़के और ‘g’ लड़कियाँ हैं। कक्षा में लड़कों की संख्या और कुल छात्रों की संख्या का अनुपात है: (क) b/(b + g) (ख) g/(b + g) (ग) b/g (घ) (b + g)/b

उत्तर: (क) प्रश्न से, कक्षा में लड़कों की संख्या = b, कक्षा में लड़कियों की संख्या = g, कक्षा में कुल छात्रों की संख्या = b + g। इसलिए, कक्षा में लड़कों की संख्या और कुल छात्रों की संख्या का अनुपात = b/(b + g)।

प्रश्न 10: यदि एक बस 4 घंटे में 160 किमी यात्रा करती है और एक ट्रेन 5 घंटे में 320 किमी यात्रा करती है, तो उनके द्वारा एक घंटे में की गई यात्रा की दूरी का अनुपात है (क) 1 : 2 (ख) 4 : 5 (ग) 5 : 8 (घ) 8 : 5

उत्तर: (c) प्रश्न में दिया गया है कि, बस 4 घंटों में 160 किमी यात्रा करती है। ट्रेन 5 घंटों में 320 किमी यात्रा करती है।

• बस द्वारा एक घंटे में यात्रा की गई दूरी = 160/4 = 40 किमी/घंटा
• ट्रेन द्वारा एक घंटे में यात्रा की गई दूरी = 320/5 = 64 किमी/घंटा

इसलिए, उनके द्वारा एक घंटे में यात्रा की गई दूरी का अनुपात = 40/64। दोनों अंश और हर को 8 से विभाजित करें। = 5/8। इसलिए, उनके द्वारा एक घंटे में यात्रा की गई दूरी का अनुपात 5: 8 है।

प्रश्न 11 से 15 में, प्रत्येक अनुपात में [ ] के बक्से में गायब संख्या खोजें:

प्रश्न 11: 3/5 = [ ]/20

मान लें कि गायब संख्या y है। तब, (3/5) = (y/20)। क्रॉस गुणन के द्वारा, (3 × 20)/5 = y।

• y = 60/5
• दोनों अंश और हर को 5 से विभाजित करें।
• y = 12

इसलिए, 3/5 = [12]/20।

प्रश्न 12: [ ]/18 = 2/9

मान लें कि गायब संख्या y है। तब, y/18 = 2/9। क्रॉस गुणन के द्वारा, y = (2 × 18)/9।

• y = 36/9
• दोनों अंश और हर को 9 से विभाजित करें।
• y = 4

इसलिए, [4]/18 = 2/9।

प्रश्न 13: 8/[ ] = 3.2/4

मान लें कि गायब संख्या y है। तब, 8/y = 3.2/4। क्रॉस गुणन के द्वारा, y = (8 × 4)/3.2।

• y = 32/3.2
• y = 320/32
• दोनों अंश और हर को 32 से विभाजित करें।
• y = 10

इसलिए, 8/[10] = 3.2/4।

प्रश्न 14: [ ]/45 = 16/40 = 24/[ ]

पहले दो अनुपात पर विचार करें [ ]/45 = 16/40। मान लें कि गायब संख्या P है। तब, P/45 = 16/40। क्रॉस गुणन के द्वारा, P = (16 × 45)/40।

• P = 720/40
• P = 72/4
• दोनों अंश और हर को 4 से विभाजित करें।
• P = 18

इसलिए, [18]/45 = 16/40। अब, अंतिम दो अनुपात पर विचार करें, 16/40 = 24/[ ]। मान लें कि गायब संख्या Q है। तब, 16/40 = 24/Q। क्रॉस गुणन के द्वारा, Q = (24 × 40)/16।

• Q = 960/16
• दोनों अंश और हर को 16 से विभाजित करें।
• Q = 60

इसलिए, 16/40 = 24/[60]।

प्रश्न 15: 16/36 = [ ]/63 = 36/[ ] = [ ]/117

पहले दो अनुपातों पर विचार करें 16/36 = [ ]/63। मान लें कि गायब संख्या को P कहते हैं। तब, 16/36 = P/63। क्रॉस गुणा करने पर हम प्राप्त करते हैं, P = (16 × 63)/36।

P = 1008/36। दोनों अंश और भाजक को 36 से विभाजित करें।

P = 28। इसलिए, 16/36 = [28]/63। अब, मध्य दो अनुपातों पर विचार करें, 28/63 = 36/[ ]। मान लें कि गायब संख्या को Q कहते हैं। तब, 28/63 = 36/Q। क्रॉस गुणा करने पर हम प्राप्त करते हैं, Q = (36 × 63)/28।

Q = 2268/28। दोनों अंश और भाजक को 28 से विभाजित करें।

Q = 81। इसलिए, 28/63 = 36/[81]। अंतिम दो अनुपातों पर विचार करें 36/81 = [ ]/117। मान लें कि गायब संख्या को R कहते हैं। तब, 36/81 = R/117। क्रॉस गुणा करने पर हम प्राप्त करते हैं, P = (36 × 117)/81।

P = 4212/81। दोनों अंश और भाजक को 81 से विभाजित करें।

P = 52। इसलिए, 36/81 = [52]/117। इस प्रकार, 16/36 = [28]/63 = 36/[81] = [52]/117।

प्रश्न 16 से 34 तक, बताएं कि दिए गए कथन सत्य (T) हैं या असत्य (F)।

प्रश्न 16: 3/8 = 15/40

सत्य।

दो भिन्नों पर विचार करें, 3/8 = 15/40। 15/40 को और सरल बनाने पर, दोनों अंश और भाजक को 5 से विभाजित करने पर हमें मिलता है, = 3/8। इसलिए, 3/8 = 3/8।

प्रश्न 17: 4 : 7 = 20 : 35

प्रश्न 18: 0.2 : 5 = 2 : 0.5

असत्य।

प्रश्न 19: 3 : 33 = 33 : 333

प्रश्न 20: 15m : 40m = 35m : 65m

प्रश्न 21: 27cm² : 57cm² = 18cm : 38cm

प्रश्न 22: 5kg : 7.5kg = Rs 7.50 : Rs 5

प्रश्न 23: 20g : 100g = 1 metre : 500cm

प्रश्न 24: 12 घंटे : 30 घंटे = 8km : 20km

प्रश्न 25: 10kg से 100kg का अनुपात 1:10 है।

प्रश्न 26: 150cm से 1 metre का अनुपात 1:1.5 है।

Q27: 25kg : 20g = 50kg : 40g

Q28: 1 घंटे और 1 दिन का अनुपात 1:1 है।

Q29: अनुपात 4 : 16 अपने सबसे छोटे रूप में है।

Q30: अनुपात 5 : 4, अनुपात 4 : 5 से भिन्न है।

5: 4 ≠ 4: 5 5/4 ≠ 4/5 1.25 ≠ 0.8

Q31: एक अनुपात हमेशा 1 से अधिक होगा।

Q32: एक अनुपात 1 के बराबर हो सकता है।

Q33: यदि b : a = c : d, तो a, b, c, d अनुपात में हैं।

Q34: एक अनुपात के दो पद विभिन्न मात्राओं में हो सकते हैं।

प्रश्न 35 से 46 तक, वाक्यों को सही बनाने के लिए रिक्त स्थान भरें।

35: अनुपात ______ द्वारा तुलना का एक रूप है।

Q36: 20m : 70m = रु 8 : रु ______।

20m : 70m = रु 8 : रु 28। मान लेते हैं कि गायब संख्या P है। तब, 20m : 70m = ₹ 8 : ₹ P 20/70 = 8/P P = (70 × 8)/20 P = 560/20 P = 56/2 P = 28 इस प्रकार, 20m : 70m = रु 8 : रु 28।

Q37: एक संख्या [ ] के बॉक्स में है ऐसा कि [ ], 24, 9, 12 अनुपात में हैं। बॉक्स में संख्या _____ है।

एक संख्या [ ] के बॉक्स में है ऐसा कि [ ], 24, 9, 12 अनुपात में हैं। बॉक्स में संख्या 18 है। मान लेते हैं कि गायब संख्या ‘P’ है। तब, P, 24, 9, 12 P: 24 = 9: 12 P/24 = 9/12 9/12 को 3 से विभाजित करके सरल किया जाता है। इसलिए, P/24 = 3/4 P = (3 × 24)/4 P = 72/4 P = 18 इस प्रकार, गायब संख्या 18 है।

Q38: यदि दो अनुपात समान हैं, तो वे _____ में हैं।

यदि दो अनुपात समान हैं, तो वे अनुपात में हैं। प्रश्न 39 और 40 के लिए चित्र का उपयोग करें:

Q39: धुंधले क्षेत्र की सीमा के परिधि का अनुपात पूरे चित्र की परिधि के साथ _______ है।

छायांकित भाग की परिधि का अनुपात पूरे आकृति की परिधि के साथ 3: 7 है। आकृति से, छायांकित भाग की परिधि = 1 + 2 + 1 + 2 = 6 यूनिट। पूरे आकृति की परिधि = 3 + 4 + 3 + 4 = 14 यूनिट। फिर, छायांकित भाग की परिधि का अनुपात पूरे आकृति की परिधि के साथ = 6/14 = 3/7 = 3: 7

प्रश्न 40: छायांकित भाग के क्षेत्र का अनुपात पूरे आकृति के क्षेत्र से ______ है।

छायांकित भाग के क्षेत्र का अनुपात पूरे आकृति के क्षेत्र से 1: 6 है। छायांकित आकृति का क्षेत्र = 2 × 1 = 2 वर्ग यूनिट। पूरे आकृति का क्षेत्र = 3 × 4 = 12 वर्ग यूनिट। छायांकित भाग के क्षेत्र का अनुपात पूरे आकृति के क्षेत्र से = 2: 12 = 2/12 = 1/6 = 1: 6

प्रश्न 41: एक 24 घंटे की घड़ी में पायथन का सोने का समय चित्र में छायांकित भाग द्वारा दर्शाया गया है।

सोने के समय और जागने के समय का अनुपात ______ है।

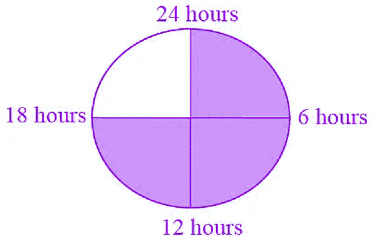
सोने के समय और जागने के समय का अनुपात 3: 1 है। आकृति से, सोने का समय = 18 घंटे। फिर, जागने का समय = 24 – 18 = 6 घंटे। इसलिए, सोने के समय और जागने के समय का अनुपात 18/6 = 3/1 = 3: 1 है।

प्रश्न 42: एक अनुपात जो सबसे कम रूप में व्यक्त किया गया है, उसके अंशों में कोई सामान्य गुणांक नहीं होता है, सिवाय ______ के।

एक अनुपात जो सबसे कम रूप में व्यक्त किया गया है, उसके अंशों में कोई सामान्य गुणांक नहीं होता है, सिवाय एक के।

प्रश्न 43: दो मात्राओं का अनुपात खोजने के लिए, उन्हें _____ यूनिट में व्यक्त किया जाना चाहिए।

दो मात्राओं का अनुपात खोजने के लिए, उन्हें समान यूनिट में व्यक्त किया जाना चाहिए।

प्रश्न 44: 5 पैसे का अनुपात 25 पैसे के समान है, जैसे 20 पैसे का अनुपात _____ के समान है।

5 पैसे का अनुपात 25 पैसे के बराबर है, जैसे कि 20 पैसे का अनुपात 100 पैसे के बराबर है। प्रश्न से, 5 पैसे : 25 पैसे = 20 पैसे : [ ] मान लेते हैं कि गायब संख्या Q है, 5 पैसे : 25 पैसे = 20 पैसे : Q

5/25 = 20/Q

Q = (20 × 25)/5

Q = 500/5

Q = 100

इसलिए, 5 पैसे का अनुपात 25 पैसे के बराबर है, जैसे कि 20 पैसे का अनुपात 100 पैसे के बराबर है।

प्रश्न 45: शनि और गुरु अपने अक्ष पर एक चक्कर लगाने में क्रमशः 9 घंटे 56 मिनट और 10 घंटे 40 मिनट लेते हैं। शनि और गुरु द्वारा लिए गए समय का अनुपात सबसे छोटे रूप में ______ है।

शनि और गुरु अपने अक्ष पर एक चक्कर लगाने में क्रमशः 9 घंटे 56 मिनट और 10 घंटे 40 मिनट लेते हैं। शनि और गुरु द्वारा लिए गए समय का अनुपात सबसे छोटे रूप में 149: 160 है। प्रश्न से, शनि एक चक्कर लगाने में 9 घंटे 56 मिनट लेते हैं। हम जानते हैं कि, 1 घंटा = 60 मिनट।

(9 × 60) + 56 = 540 + 56 = 596 मिनट

गुरु एक चक्कर लगाने में 10 घंटे 40 मिनट लेते हैं = (10 × 60) + 40 = 600 + 40 = 640 मिनट

शनि और गुरु द्वारा लिए गए समय का अनुपात सबसे छोटे रूप में = 596/640

दोनों अंश और हर को 2 से विभाजित करें, = 298/320

फिर से, दोनों अंश और हर को 2 से विभाजित करें, = 149/160

इसलिए, शनि और गुरु द्वारा लिए गए समय का अनुपात सबसे छोटे रूप में 149 : 160 है।

प्रश्न 46: 10 ग्राम कास्टिक सोडा को 100 मिलीलीटर पानी में घोलने से कास्टिक सोडा का एक घोल बनता है। 1 लीटर पानी के लिए उसी प्रकार के घोल के लिए आवश्यक कास्टिक सोडा की मात्रा ______ है।

दिया गया, 10 ग्राम कास्टिक सोडा को 100 मिलीलीटर पानी में घोलना। कास्टिक सोडा और पानी का अनुपात अनुपात में होना चाहिए।

• 10 ग्राम : 100 मिलीलीटर :: x ग्राम : 1 लीटर [∵ 1 लीटर = 1000 मिलीलीटर]

x ग्राम × 100 मिलीलीटर = 10 ग्राम × 1000 मिलीलीटर [क्रॉस गुणा द्वारा]

x = 100 ग्राम

प्रश्न 47: एक मेज की मार्क मूल्य ₹625 है और इसका बिक्री मूल्य ₹500 है। बिक्री मूल्य और मार्क मूल्य का अनुपात क्या है?

दिया गया है, मेज का मार्क मूल्य = ₹625
मेज का बिक्री मूल्य = ₹500
बिक्री मूल्य और मार्क मूल्य का अनुपात = ₹500/625 = 500/625 = 20/25 [अंश और हर को 25 से विभाजित करने पर] = 4/5 [अंश और हर को 5 से विभाजित करने पर]
∴ आवश्यक अनुपात = 4 : 5

प्रश्न 48: कौन से अनुपात के जोड़े समान हैं? और क्यों?
(i) 2/3, 4/6
(ii) 8/4, 2/1
(iii) 4/5, 12/20

(i) दिया गया जोड़ा समान है क्योंकि 4/6 का सबसे कम रूप 2/3 है और अन्य अनुपात 2/3 है।
(ii) दिया गया जोड़ा समान है क्योंकि 8/4 का सबसे कम रूप 2/1 है और अन्य अनुपात 2/1 है।
(iii) दिया गया जोड़ा समान नहीं है क्योंकि 12/20 का सबसे कम रूप 3/5 है और अन्य अनुपात 4/5 है।

प्रश्न 49: कौन सा अनुपात बड़ा है 10:21 या 21:93?

अनुपात 10:21 बड़ा है क्योंकि यह 0.476 के करीब है और 21:93 लगभग 0.225 है।

प्रश्न 50: रेशमा ने खoya और चीनी को 7:2 के अनुपात में मिलाकर 18 किलोग्राम बर्फी तैयार की। उसने कितनी खoya का उपयोग किया?

दिया गया है, बर्फी की मात्रा = 18 किलोग्राम और खoya : चीनी = 7:2
अनुपात का कुल = 7 + 2 = 9
खoya की मात्रा = (18/9) × 7 = 14 किलोग्राम
तो, रेशमा ने 14 किलोग्राम खoya का उपयोग किया।

प्रश्न 51: एक रेखा खंड जिसकी लंबाई 56 सेंटीमीटर है, को 2:5 के अनुपात में दो भागों में विभाजित किया जाना है। प्रत्येक भाग की लंबाई ज्ञात कीजिए।

दिया गया है, रेखा खंड की लंबाई = 56 सेंटीमीटर
दो भागों का अनुपात = 2:5
अनुपात का योग = 2 + 5 = 7
पहले भाग की लंबाई = (2/7) × 56 = 16 सेंटीमीटर
दूसरे भाग की लंबाई = (5/7) × 56 = 40 सेंटीमीटर

प्रश्न 52: मानव में दूध के दांतों की संख्या 20 है और स्थायी दांतों की संख्या 32 है। दूध के दांतों की संख्या और स्थायी दांतों की संख्या का अनुपात ज्ञात कीजिए।

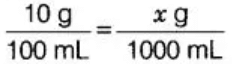
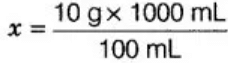
मनुष्यों में दूध के दांतों की संख्या = 20

मनुष्यों में स्थायी दांतों की संख्या = 32

दूध के दांतों की संख्या और स्थायी दांतों की संख्या का अनुपात = 20/32 = 5/8 [अंक और हर को 4 से विभाजित करने पर] = 5 : 8

प्रश्न 53: लिंगानुपात को जनसंख्या में 1000 पुरुषों पर महिलाओं की संख्या के रूप में परिभाषित किया जाता है। यदि एक नगर में 4000 पुरुषों पर 3732 महिलाएं हैं, तो लिंगानुपात ज्ञात करें।

एक नगर में 4000 पुरुषों पर 3732 महिलाओं का लिंगानुपात इस प्रकार दिया गया है, = 3732/4000

प्रश्न 54: एक वर्ष में, रवि की आय Rs. 360000 है और उसने Rs. 24000 आयकर के रूप में चुकाया है। (क) उसकी आय और आयकर का अनुपात ज्ञात करें। (ख) आयकर और आयकर चुकाने के बाद आय का अनुपात ज्ञात करें।

(क) आय और आयकर का अनुपात = 360000/24000 = 15/1

(ख) आयकर और आयकर चुकाने के बाद आय का अनुपात = 24000/336000 = 3/42

प्रश्न 55: रमेश प्रति माह Rs 28000 कमाता है। उसकी पत्नी रमा प्रति माह Rs 36000 कमाती है। (क) रमेश की आय और उनकी कुल आय का अनुपात ज्ञात करें। (ख) रमा की आय और उनकी कुल आय का अनुपात ज्ञात करें।

(क) रमेश की आय और रमेश तथा रमा की कुल आय का अनुपात = 28000/64000 = 9/16

(ख) रमा की आय और रमेश तथा रमा की कुल आय का अनुपात = 36000/64000 = 7/16

प्रश्न 56: एक कंपनी में 288 व्यक्ति काम कर रहे हैं, जिनमें 112 पुरुष हैं और शेष महिलाएं हैं। (क) पुरुषों की संख्या और महिलाओं की संख्या का अनुपात ज्ञात करें। (ख) पुरुषों की संख्या और कुल व्यक्तियों की संख्या का अनुपात ज्ञात करें। (ग) महिलाओं की संख्या और कुल व्यक्तियों की संख्या का अनुपात ज्ञात करें।

कंपनी में काम करने वाले व्यक्तियों की संख्या = 288

कंपनी में पुरुषों की कुल संख्या = 112

कंपनी में महिलाओं की कुल संख्या = 176

(क) पुरुषों की संख्या और महिलाओं की संख्या का अनुपात = 112/176 = 7/11

(ख) महिलाओं की संख्या और कुल व्यक्तियों की संख्या का अनुपात = 176/288 = 44/57

प्रश्न 57: एक आयताकार कागज़ की शीट की लंबाई 1.2 मीटर और चौड़ाई 21 सेंटीमीटर है। कागज़ की चौड़ाई और उसकी लंबाई का अनुपात ज्ञात करें।

दी गई जानकारी: आयताकार शीट की लंबाई = 1.2 मीटर [1 मीटर = 100 सेंटीमीटर] = 1.2 x 100 सेंटीमीटर = 120 सेंटीमीटर
आयताकार शीट की चौड़ाई = 21 सेंटीमीटर
चौड़ाई और लंबाई का अनुपात = 21 सेंटीमीटर / 120 सेंटीमीटर = 7/40 = 7:40 [न्यूमरेटर और डिनॉमिनेटर को 3 से विभाजित करने पर]

प्रश्न 58: एक स्कूटर 3 घंटे में 120 किमी की यात्रा करता है और एक ट्रेन 2 घंटे में 120 किमी की यात्रा करती है। उनकी गति का अनुपात ज्ञात करें। (संकेत: गति = यात्रा की गई दूरी / लिया गया समय)

स्कूटर की गति = 120/3 = 40 किमी/घंटा
ट्रेन की गति = 120/2 = 60 किमी/घंटा
अब, स्कूटर की गति और ट्रेन की गति का अनुपात = 40/60 = 2/3

प्रश्न 59: एक कार्यालय सुबह 9 बजे खुलता है और शाम 5:30 बजे बंद होता है, जिसमें 30 मिनट का लंच ब्रेक होता है। कार्यालय में कुल समय के मुकाबले लंच ब्रेक का अनुपात क्या है?

दी गई जानकारी के अनुसार, कार्यालय में कुल समय = सुबह 9 बजे से दोपहर 12 बजे और दोपहर 12 बजे से शाम 5 बजे तक। इसका मतलब है कुल समय = 3 घंटे + 5 घंटे = 8 घंटे। चूंकि 1 घंटा = 60 मिनट है, तो 8 घंटे = 8 × 60 = 480 मिनट।
अब, लंच अंतराल और कुल समय का अनुपात = 30/480 = 1/16

प्रश्न 60: 3 मीटर लंबे डंडे की छाया 4 मीटर लंबी है। उसी समय में, यदि एक झंडा खंभे की छाया 24 मीटर लंबी है, तो झंडा खंभा कितनी ऊँचाई का है?

यहाँ दी गई जानकारी: डंडे की छाया की लंबाई = 4 मीटर
डंडे की लंबाई = 3 मीटर
साथ ही, झंडा खंभे की छाया की लंबाई = 24 मीटर
अब, झंडा खंभे की लंबाई = (3 x 24)/4 = 18 मीटर

प्रश्न 61: एक नुस्खे में 6 लोगों के लिए एक केक बनाने के लिए 1 कप दूध और 1 2/2 कप आटे की आवश्यकता होती है। 8 लोगों के लिए समान केक बनाने के लिए कितने कप आटे और दूध की आवश्यकता होगी?

जैसा कि दिया गया है, 1 कप दूध और 2 1/2 कप आटा एक केक बनाने के लिए है जो छह व्यक्तियों के लिए है। एक व्यक्ति के लिए आवश्यक सामग्री होगी, दूध = 1/6 कप, आटा = 5/12 कप। अब, 8 व्यक्तियों के लिए, दूध 8 x (1/6) = 4/3 कप, आटा = 10/3 कप। इसलिए, हमें 4/3 कप दूध और 10/3 कप आटे की आवश्यकता है जो आठ व्यक्तियों के लिए केक बनाए।

प्रश्न 62: एक स्कूल में, बड़े कक्षाओं की संख्या और छोटे कक्षाओं की संख्या का अनुपात 3 : 4 है। यदि छोटे कक्षाओं की संख्या 20 है, तो बड़े कक्षाओं की संख्या ज्ञात करें।

दिया गया है, बड़े कक्षाओं और छोटे कक्षाओं की संख्या का अनुपात = 3:4, छोटे कक्षाओं की संख्या = 20। मान लें कि कक्षाएँ x के गुणांक हैं। तो, बड़े कक्षाएँ = 3x, छोटे कक्षाएँ = 4x। प्रश्न के अनुसार, 4x = 20 => x = 20/4 = 5। इसलिए, बड़े कक्षाओं की संख्या = 3x = 3 x 5 = 15।

प्रश्न 63: समिरा जैनपथ चौक पर प्रतिदिन समाचार पत्र बेचती है। एक विशेष दिन, उसके पास 312 समाचार पत्र थे जिनमें से 216 अंग्रेजी में हैं और शेष हिंदी में हैं। (क) अंग्रेजी समाचार पत्रों की संख्या का हिंदी समाचार पत्रों की संख्या के साथ अनुपात ज्ञात करें। (ख) हिंदी समाचार पत्रों की संख्या का कुल समाचार पत्रों की संख्या के साथ अनुपात ज्ञात करें।

दिया गया है, कुल समाचार पत्र = 312, अंग्रेजी समाचार पत्र = 216, हिंदी समाचार पत्र = कुल समाचार पत्र - अंग्रेजी में समाचार पत्र = 312 - 216 = 96। (क) अंग्रेजी समाचार पत्रों की संख्या का हिंदी समाचार पत्रों की संख्या के साथ अनुपात = 216/96 = 9/4 = 9:4 [संख्यात्मक और हर के 24 से भाग देने पर] (ख) हिंदी समाचार पत्रों की संख्या का कुल समाचार पत्रों की संख्या के साथ अनुपात = 96/312 = 4/13 = 4:13।

प्रश्न 64: एक स्कूल के छात्र विभिन्न धार्मिक पृष्ठभूमियों से संबंधित हैं। हिंदू छात्रों की संख्या 288, मुस्लिम छात्रों की संख्या 252, सिख छात्रों की संख्या 144 और ईसाई छात्रों की संख्या 72 है। (क) हिंदू छात्रों की संख्या का ईसाई छात्रों की संख्या के साथ अनुपात ज्ञात करें। (ख) मुस्लिम छात्रों की संख्या का कुल छात्रों की संख्या के साथ अनुपात ज्ञात करें।

दी गई जानकारी: हिंदू छात्रों की संख्या = 288
मुस्लिम छात्रों की संख्या = 252
सिख छात्रों की संख्या = 144
ईसाई छात्रों की संख्या = 72
कुल छात्रों की संख्या = 288 + 252 + 144 + 72 = 756

• (a) हिंदू छात्रों और ईसाई छात्रों की संख्या का अनुपात = 288/72 = 4/1 = 4:1 [अंश और हर को 72 से विभाजित करने पर]
• (b) मुस्लिम छात्रों की संख्या और कुल छात्रों की संख्या का अनुपात = 252/756 = 1/3 = 1:3 [अंश और हर को 252 से विभाजित करने पर]

प्रश्न 65: जब चिन्मय ने मुंबई के चौपाटी पर एक छुट्टी के दिन का दौरा किया, तो उसने देखा कि उत्तर भारतीय खाने की स्टॉल्स की संख्या और दक्षिण भारतीय खाने की स्टॉल्स की संख्या का अनुपात 5:4 है। यदि कुल खाने की स्टॉल्स की संख्या 117 है, तो प्रत्येक प्रकार की खाने की स्टॉल्स की संख्या ज्ञात करें।

दी गई जानकारी: उत्तर भारतीय खाने की स्टॉल्स और दक्षिण भारतीय खाने की स्टॉल्स का अनुपात = 5:4
कुल खाने की स्टॉल्स = 117
कुल अनुपात = 5 + 4 = 9

• उत्तर भारतीय खाने की स्टॉल्स = (5/9) × 117 = 65
• दक्षिण भारतीय खाने की स्टॉल्स = (4/9) × 117 = 52

प्रश्न 66: रामलीला मैदान के पार्किंग स्टैंड पर, कार्तिक ने गिनती की कि वहां 115 साइकिलें, 75 स्कूटर और 45 बाइक हैं। कुल वाहनों की संख्या के मुकाबले साइकिलों की संख्या का अनुपात ज्ञात करें।

दी गई जानकारी: पार्किंग स्टैंड पर, साइकिलों की संख्या = 115
स्कूटर = 75
बाइक = 45
कुल वाहनों की संख्या = 115 + 75 + 45 = 235

• साइकिलों की संख्या और कुल वाहनों की संख्या का अनुपात = 115/235 = 23/47 = 23:47 [अंश और हर को 5 से विभाजित करने पर]

प्रश्न 67: एक ट्रेन अजमेर से जयपुर जाने में 2 घंटे लेती है, जो 130 किमी दूर हैं। यदि ट्रेन समान गति से यात्रा कर रही है, तो दिल्ली से भोपाल जाने में कितना समय लगेगा, जो 780 किमी दूर हैं?

अजमेर से जयपुर जाने में लगने वाला समय = 2 घंटे
अजमेर और जयपुर के बीच की दूरी = 130 किमी
दिल्ली और भोपाल के बीच की दूरी = 780 किमी
अब, ट्रेन की गति = 130/2 किमी/घंटा = 65 किमी/घंटा
इसलिए, दिल्ली से भोपाल जाने में ट्रेन का समय = 780/65 = 12 घंटे

प्रश्न 68: एक स्कूल के मैदान की लंबाई और चौड़ाई क्रमशः 150 मीटर और 90 मीटर है, जबकि एक मेले के मैदान की लंबाई और चौड़ाई क्रमशः 210 मीटर और 126 मीटर है। क्या ये माप अनुपात में हैं?

एक स्कूल के मैदान की लंबाई और चौड़ाई का अनुपात = 150/90 = 5/3
एक मेले के मैदान की लंबाई और चौड़ाई का अनुपात = 210/126 = 5/3
इस प्रकार, दिए गए माप अनुपात में हैं।

प्रश्न 69: चित्र 8.4 में महाद्वीपों के तुलनात्मक क्षेत्र दिए गए हैं: (a) अफ्रीका से यूरोप का क्षेत्र का अनुपात क्या है?
(b) ऑस्ट्रेलिया से एशिया का क्षेत्र का अनुपात क्या है?
(c) अंटार्कटिका से उत्तर अमेरिका और दक्षिण अमेरिका के संयुक्त क्षेत्र का अनुपात क्या है?

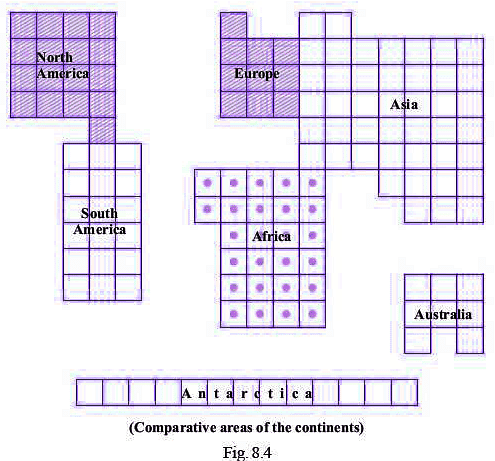
(a) दिए गए आंकड़ों से, अफ्रीका से यूरोप का क्षेत्र का अनुपात = 13/5
(b) दिए गए आंकड़ों से, ऑस्ट्रेलिया से एशिया का क्षेत्र का अनुपात = 2/11
(c) दिए गए आंकड़ों से, अंटार्कटिका से उत्तर अमेरिका और दक्षिण अमेरिका के संयुक्त क्षेत्र का अनुपात = 13/35

प्रश्न 70: एक चाय व्यापारी दो प्रकार की चाय का मिश्रण करता है, जिनकी कीमत क्रमशः 234 रुपये और 130 रुपये प्रति किलोग्राम है, उनके लागत के अनुपात में। यदि मिश्रण का वजन 84 किलोग्राम है, तो प्रत्येक प्रकार की चाय का वजन ज्ञात करें।

दिया गया, दो प्रकार की चाय की कीमत = 234 रुपये और 130 रुपये
उनकी कीमतों का अनुपात = 234/130 = 9/5 = 9:5 [संख्यात्मक और हर के 26 से विभाजन करने पर]
कुल मिश्रण का वजन = 84 किलोग्राम
कुल अनुपात = 9 + 5 = 14
पहली प्रकार की चाय का वजन = (9/14) x 84 = 54 किलोग्राम
दूसरी प्रकार की चाय का वजन = (5/14) x 84 = 30 किलोग्राम

प्रश्न 71: एक मिश्र धातु में केवल जस्ता और तांबा है और उनका अनुपात 7:9 है। यदि मिश्र धातु का वजन 8 किलोग्राम है, तो मिश्र धातु में तांबे का वजन ज्ञात कीजिए।

दिया गया है, मिश्र धातु में जस्ता और तांबे का अनुपात = 7:9 और मिश्र धातु का वजन = 8 किलोग्राम। मान लीजिए कि मिश्र धातु में जस्ते और तांबे का वजन क्रमशः 7x और 9x है, जहाँ x वजन का गुणांक है। फिर, कुल वजन = 7x + 9x = 16x = 8 किलोग्राम => x = ½ किलोग्राम। तांबे का वजन = 9x = 9 × (1/2) = 4 ½ किलोग्राम। अतः, तांबे का वजन 4 ½ किलोग्राम है।

प्रश्न 72: निम्नलिखित आकृति में, प्रत्येक विभाजन 1 सेंटीमीटर को दर्शाता है:

निम्नलिखित दूरी का अनुपात संख्यात्मक रूप से व्यक्त कीजिए: (i) AC : AF (ii) AG : AD (iii) BF : AI (iv) CE : DI

(i) AC/AF = 2/5 (ii) AG/AD = 2/1 (iii) BF/AI = 1/2 (iv) CE/DI = 2/5

प्रश्न 73: दो संख्याएँ ज्ञात कीजिए, जिनका योग 100 है और अनुपात 9:16 है।

मान लीजिए दो संख्याएँ 9x और 16x हैं, जिनका योग 100 है। ⇒ 9x + 16x = 100 ⇒ 25x = 100 ⇒ x = 4

प्रश्न 74: चित्र 8.6 (i) और चित्र 8.6 (ii) में, छायांकित भाग के क्षेत्रफल का अनुपात पूरे आकृति के क्षेत्रफल से ज्ञात कीजिए:

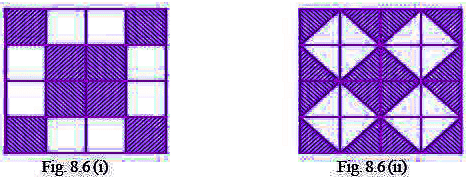
(i) छायांकित भाग के क्षेत्रफल का अनुपात पूरे आकृति के क्षेत्रफल के = 8/16 = 1/2 (ii) छायांकित भाग के क्षेत्रफल का अनुपात पूरे आकृति के क्षेत्रफल के = 16/32 = 1/2

प्रश्न 75: एक टाइपिस्ट को 40 पृष्ठों का एक पाण्डुलिपि टाइप करना है। उसने पाण्डुलिपि के 30 पृष्ठ टाइप कर लिए हैं। टाइप किए गए पृष्ठों की संख्या और बचे पृष्ठों की संख्या का अनुपात क्या है?

टाइप करने के लिए कुल पृष्ठ = 40 टाइप किए गए पृष्ठ = 30 बचे पृष्ठ = 40 – 30 = 10। टाइप किए गए पृष्ठों की संख्या और बचे पृष्ठों की संख्या का अनुपात = 30/10 = 3/1 = 3:1।

प्रश्न 76: टाइल्स के एक पुष्प डिज़ाइन में, जिनका आकार 40 सेमी x 60 सेमी है (देखें चित्र 8.7), निम्नलिखित का अनुपात खोजें: (क) shaded portion (छायांकित भाग) का परिमाप पूरे डिज़ाइन के परिमाप के मुकाबले। (ख) shaded portion (छायांकित भाग) का क्षेत्रफल unshaded portion (अछायांकित भाग) के क्षेत्रफल के मुकाबले।

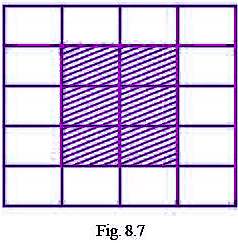
(क) shaded region (छायांकित क्षेत्र) का परिमाप = 2(20 + 36) = 112 सेमी। पूरे डिज़ाइन का परिमाप = 2(40 + 60) = 200 सेमी। अब, shaded portion (छायांकित भाग) के परिमाप का अनुपात पूरे डिज़ाइन के परिमाप के मुकाबले = 112/200 = 14/25। (ख) shaded portion (छायांकित भाग) का क्षेत्रफल = 20 x 36 = 720 वर्ग सेमी। unshaded portion (अछायांकित भाग) का क्षेत्रफल = (40 x 60) - 720 = 1680 वर्ग सेमी। अब, shaded portion (छायांकित भाग) के क्षेत्रफल का अनुपात unshaded portion (अछायांकित भाग) के क्षेत्रफल के मुकाबले = 720/1680 = 3/7।

प्रश्न 77: चित्र 8.8 में, (क) shaded portion I (छायांकित भाग I) का shaded portion II (छायांकित भाग II) के मुकाबले अनुपात क्या है? (ख) shaded portion II (छायांकित भाग II) का shaded portion III (छायांकित भाग III) के मुकाबले अनुपात क्या है? (ग) shaded portions I और II (छायांकित भाग I और II) का shaded portion III (छायांकित भाग III) के मुकाबले अनुपात क्या है?

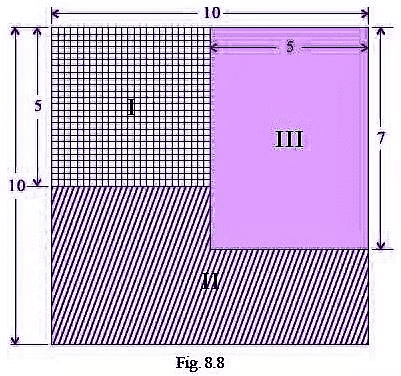
(क) shaded portion I (छायांकित भाग I) के क्षेत्र का अनुपात shaded portion II (छायांकित भाग II) के मुकाबले = 5/8। (ख) shaded portion II (छायांकित भाग II) के क्षेत्र का अनुपात shaded portion III (छायांकित भाग III) के मुकाबले = 8/7। (ग) shaded portions I और II (छायांकित भाग I और II) का अनुपात shaded portion III (छायांकित भाग III) के मुकाबले = 13/7।

प्रश्न 78: एक कार 15 लीटर पेट्रोल में 240 किलोमीटर यात्रा कर सकती है। 25 लीटर पेट्रोल में यह कितनी दूरी तय करेगी?

15 लीटर पेट्रोल में कार द्वारा तय की गई दूरी = 240 किलोमीटर। 25 लीटर पेट्रोल में कार द्वारा तय की गई दूरी = (240/15) x 25 = 400 किलोमीटर।

प्रश्न 79: बच्चू मांझी 8 महीनों में 24000 रुपये कमाते हैं। इस दर से, (क) वे एक वर्ष में कितना कमाते हैं? (ख) वे 42000 रुपये कितने महीनों में कमाते हैं?

बच्चू मांझी द्वारा 8 महीनों में कमाई गई राशि = Rs. 24000

(a) बच्चू मांझी द्वारा 12 महीनों में कमाई गई राशि = (24000/8) x 12 = Rs. 36000

(b) बच्चू मांझी द्वारा 8 महीनों में कमाई गई राशि = Rs. 24000

बच्चू मांझी द्वारा कमाई गई राशि = (8/24000) x 42000 = 16 महीने

प्रश्न 80: 8 हेक्टेयर भूमि से गेहूं की उपज 360 क्विंटल है। 540 क्विंटल की उपज के लिए कितने हेक्टेयर भूमि की आवश्यकता होगी?

गेहूं की 360 क्विंटल उपज के लिए आवश्यक भूमि = 8 हेक्टेयर

गेहूं की 540 क्विंटल उपज के लिए आवश्यक भूमि = (8/360) x 540 = 12 हेक्टेयर

प्रश्न 81: पृथ्वी अपने अक्ष पर 24 घंटे में 360º घूमती है। 2 घंटे में यह कितने डिग्री घूमेगी?

24 घंटे में, पृथ्वी घूमती है = 360 डिग्री

2 घंटे में, पृथ्वी घूमती है = (360/24) x 2 = 30 डिग्री

प्रश्न 82: शिवांगी को एनीमिया है क्योंकि उसके रक्त में हीमोग्लोबिन का स्तर सामान्य सीमा से कम है। डॉक्टर ने उसे दिन में दो बार एक आयरन टैबलेट लेने की सलाह दी है। यदि 10 टैबलेट की कीमत Rs. 17 है, तो 15 दिनों के लिए उसे अपने चिकित्सा बिल के लिए कितना भुगतान करना होगा?

प्रतिदिन की आवश्यकता अनुसार टैबलेट = 2

15 दिनों के लिए आवश्यक टैबलेट = 15 x 2 = 30

10 टैबलेट की लागत = Rs. 17

30 टैबलेट की लागत = (17/10) x 30 = 51

प्रश्न 83: केंद्रीय विद्यालय में कक्षा VI की त्रैमासिक फीस Rs. 540 है। सात महीनों की फीस कितनी होगी?

कक्षा VI की त्रैमासिक फीस = Rs. 540

सात महीनों की फीस = (540/4) x 7 = Rs. 945

प्रश्न 84: एक चुनाव में, दो उम्मीदवारों के लिए डाले गए वोटों का अनुपात 5 : 7 था। यदि सफल उम्मीदवार को 20734 वोट मिले, तो उसके प्रतिद्वंदी को कितने वोट मिले?

जैसा कि दिया गया है, दो उम्मीदवारों के लिए डाले गए वोटों का अनुपात = 5:7। मान लें कि दो उम्मीदवारों द्वारा प्राप्त वोट = 5x और 7x। साथ ही, सफल उम्मीदवारों द्वारा प्राप्त वोट = 20734। इसका तात्पर्य है, 7x = 20734। x = 2962। प्रतिकूल उम्मीदवार द्वारा प्राप्त वोट = 5 × 2962 = 14810।

प्रश्न 85: एक धातु की पाइप जिसकी लंबाई 3 मीटर है, का वजन 7.6 किलोग्राम पाया गया। 7.8 मीटर लंबी समान प्रकार की पाइप का वजन क्या होगा?

3 मीटर लंबी पाइप का वजन = 7.6 किलोग्राम।
7.8 मीटर लंबी पाइप का वजन = (7.6/3) × 7.8 = 19.76 किलोग्राम।

प्रश्न 86: रास्पबेरी जेली के लिए एक नुस्खा में 5 कप रास्पबेरी जूस और 2(1/2) कप चीनी की आवश्यकता होती है। 6 कप जूस के लिए आवश्यक चीनी की मात्रा ज्ञात करें।

5 कप रास्पबेरी जूस के लिए आवश्यक चीनी = 5/2 कप।
6 कप रास्पबेरी जूस के लिए आवश्यक चीनी = 5/(2×5) × 6 = 3 कप।

प्रश्न 87: एक किसान ने एक खेत में 1890 टमाटर के पौधे लगाए हैं, प्रत्येक पंक्ति में 63 पौधे हैं। एक विशेष प्रकार के कीड़े ने प्रत्येक पंक्ति में 18 पौधों को नष्ट कर दिया। कीड़े ने पूरे खेत में कितने पौधे नष्ट किए?

मान लें कि पंक्तियों की संख्या = x।
इसका तात्पर्य है, कुल पौधों की संख्या = (प्रत्येक पंक्ति में पौधों की संख्या) × (पंक्तियों की संख्या)।
1890 = 63x।
x = 1890/63 = 30।
तो, पंक्तियों की संख्या = 30।
प्रत्येक पंक्ति में कीड़े द्वारा नष्ट किए गए पौधे = 18।
इसलिए, कीड़े द्वारा नष्ट किए गए कुल पौधे = 18 × 30 = 540।

प्रश्न 88: एक कमरे की फर्श की लंबाई और चौड़ाई क्रमशः 5 मीटर और 3 मीटर है। फर्श को आंशिक रूप से ढकने के लिए 40 टाइलें, प्रत्येक का क्षेत्रफल 1/16 मीटर², का उपयोग किया गया है। फर्श के टाइल वाले और गैर-टाइल वाले भाग का अनुपात ज्ञात करें।

दिया गया, कमरे की फर्श की लंबाई और चौड़ाई = 5 मीटर और 3 मीटर।
तो फर्श का क्षेत्रफल = 3 × 5 = 15 मीटर²।
एक टाइल का क्षेत्रफल = 1/16 मीटर²।
इसलिए, 40 टाइलों द्वारा ढकी गई फर्श का क्षेत्रफल = (1/16) × 40 = 5/2 मीटर²।
टाइलों द्वारा न ढकी गई फर्श का क्षेत्रफल = 15 - 5/2 = 25/2 मीटर²।
अब, फर्श के टाइल वाले और गैर-टाइल वाले भाग का अनुपात।

प्रश्न 89: एक बढ़ई के पास एक बोर्ड था जिसका माप 3 मीटर × 2 मीटर था। उसने 250 सेमी × 90 सेमी का एक आयताकार टुकड़ा काटा। काटे गए टुकड़े और शेष टुकड़े के क्षेत्र का अनुपात क्या है?

बोर्ड का माप: 3 मीटर × 2 मीटर। इसलिए, बोर्ड का क्षेत्र = 300 सेमी × 200 सेमी = 60000 वर्ग सेंटीमीटर।

बोर्ड से काटा गया आयताकार टुकड़े का माप: 250 सेमी × 90 सेमी। इसलिए, काटे गए आयताकार टुकड़े का क्षेत्र = 22500 वर्ग सेंटीमीटर।

बोर्ड के शेष भाग का क्षेत्र: 60000 - 22500 = 37500 वर्ग सेंटीमीटर।

अब, काटे गए टुकड़े और शेष टुकड़े के क्षेत्र का अनुपात = 22500 / 37500।