NCERT Exemplar: Three Dimensional Geometry | Mathematics (Maths) for JEE Main & Advanced PDF Download
| Table of contents |

|
| Short Answer Type Questions |

|
| Long Answer Type Questions |

|
| Objective Type Questions |

|
| Fill in the blanks |

|
| State True or False for the statements |

|
Short Answer Type Questions
Q.1. Find the position vector of a point A in space such that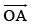 is inclined at 60º to OX and at 45° to OY and
is inclined at 60º to OX and at 45° to OY and = 10 units.
= 10 units.
Ans.
Let α = 60°, β = 45° and the angle inclined to OZ axis be γ
We know that
cos2 α + cos2 β + cos2 γ = 1
⇒ cos2 60° + cos2 45° + cos2 γ = 1
⇒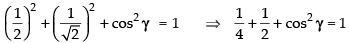
⇒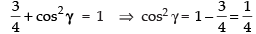
∴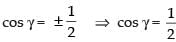
(Rejecting cos γ =
∴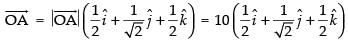

Hence, the position vector of A is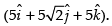
Q.2. Find the vector equation of the line which is parallel to the vector 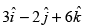 and which passes through the point (1,–2,3).
and which passes through the point (1,–2,3).
Ans.
We know that the equation of line is
Here, 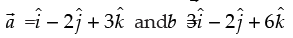
Hence, the required equation is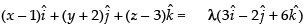
Q.3. Show that the lines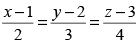 and
and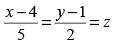 intersect.
intersect.
Also, find their point of intersection.
Ans.
The given equations are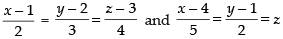
Let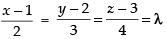
∴ x = 2λ + 1, y = 3λ + 2 and z = 4λ + 3
and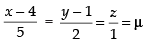
⇒ x = 5μ + 4, y = 2μ + 1 and z = μ
If the two lines intersect each other at one point,
then 2λ + 1 = 5μ + 4
⇒ 2λ – 5μ = 3 ...(i)
3λ + 2 = 2μ + 1
⇒ 3λ – 2μ = – 1 ...(ii)
and 4λ + 3 = μ
⇒ 4λ – μ = – 3 ...(iii)
Solving eqns. (i) and (ii) we get
2λ – 5μ = 3 [multiply by 3]
⇒3λ – 2μ = – 1 [multiply by 2]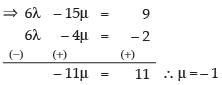
Putting the value of m in eq. (i) we get,
2λ – 5(– 1) = 3
⇒ 2λ + 5 = 3
⇒ 2λ = – 2 ∴ λ = – 1
Now putting the value of λ and m in eq. (iii) then
4(– 1) – (– 1) = – 3
– 4 + 1 = – 3
– 3 = – 3 (satisfied)
∴ Coordinates of the point of intersection are
x = 5 (– 1) + 4 = – 5 + 4 = – 1
y = 2(– 1) + 1 = – 2 + 1 = – 1
z = – 1
Hence, the given lines intersect each other at (– 1, – 1, – 1).
Alternately: If two lines intersect each other at a point, then the shortest distance between them is equal to 0.
For this we will use SD =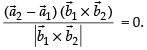
Q.4. Find the angle between the lines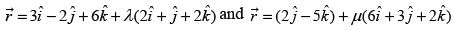
Ans.
Here,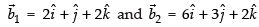
∴
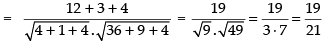
∴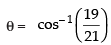
Hence, the required angle is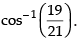
Q.5. Prove that the line through A (0, –1, –1) and B (4, 5, 1) intersects the line through C (3, 9, 4) and D (– 4, 4, 4).
Ans.
Given points are A(0, – 1, – 1) and B(4, 5, 1) C(3, 9, 4) and D(– 4, 4, 4)
Cartesian form of equation AB is
and its vector form is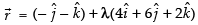
Similarly, equation of CD is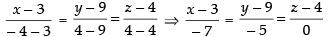
and its vector form is
Now, here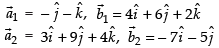
Shortest distance between AB and CD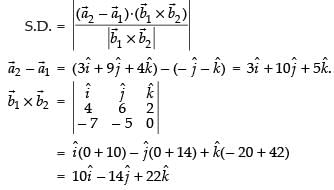

∴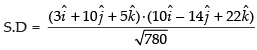
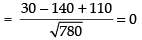
Hence, the two lines intersect each other.
Q.6. Prove that the lines x = py + q, z = ry + s and x = p′y + q′, z = r′y + s′ are perpendicular if pp′ + rr′ + 1 = 0.
Ans.
Given that: x = py + q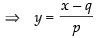
and z = ry + s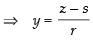
∴ the equation becomes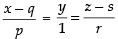 in which d’ratios are a1 = p, b1 = 1, c1 = r
in which d’ratios are a1 = p, b1 = 1, c1 = r
Similarly x = p′y + q′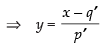
and z = r′y + s′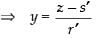
∴ the equation becomes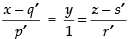 in which a2 = p′, b2 = 1, c2 = r′
in which a2 = p′, b2 = 1, c2 = r′
If the lines are perpendicular to each other, then
a1a2 + b1b2 + c1c2 = 0
pp′ + 1.1 + rr′ = 0
Hence, pp′ + rr′ + 1 = 0 is the required condition.
Q.7. Find the equation of a plane which bisects perpendicularly the line joining the points A (2, 3, 4) and B (4, 5, 8) at right angles.
Ans.
Given that A(2, 3, 4) and B(4, 5, 8)
Coordinates of mid-point C are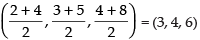
Now direction ratios of the normal to the plane
= direction ratios of AB
= 4 – 2, 5 – 3, 8 – 4 = (2, 2, 4)
Equation of the plane is
a(x – x1) + b(y – y1) + c(z – z1) = 0
⇒ 2(x – 3) + 2(y – 4) + 4(z – 6) = 0
⇒ 2x – 6 + 2y – 8 + 4z – 24 = 0
⇒ 2x + 2y + 4z = 38 ⇒ x + y + 2z = 19
Hence, the required equation of plane is
x + y + 2z = 19 or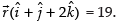
Q.8. Find the equation of a plane which is at a distance 3 √3 units from origin and the normal to which is equally inclined to coordinate axis.
Ans.
Since, the normal to the plane is equally inclined to the axes
∴ cos α = cos β = cos γ
⇒ cos2 α + cos2 α + cos2 α = 1
⇒ 3 cos2 α = 1 ⇒ cos a = 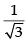
⇒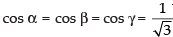
So, the normal is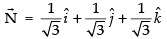
∴ Equation of the plane is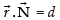
⇒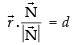
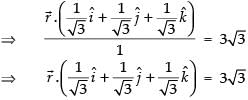
⇒ x + y+ z = 3√3.√3
⇒ x + y+z = 9
Hence, the required equation of plane is x + y + z = 9.
Q.9. If the line drawn from the point (–2, – 1, – 3) meets a plane at right angle at the point (1, – 3, 3), find the equation of the plane.
Ans.
Direction ratios of the normal to the plane are
(1 + 2, – 3 + 1, 3 + 3) Þ (3, - 2, 6)
Equation of plane passing through one point (x1, y1, z1) is
a(x – x1) + b(y – y1) + c(z – z1) = 0
⇒ 3(x – 1) – 2(y + 3) + 6(z – 3) = 0
⇒ 3x – 3 – 2y – 6 + 6z – 18 = 0
⇒ 3x – 2y + 6z – 27 = 0 ⇒ 3x - 2y + 6z = 27
Hence, the required equation is 3x - 2y + 6z = 27.
Q.10. Find the equation of the plane through the points (2, 1, 0), (3, –2, –2) and (3, 1, 7).
Ans.
Since, the equation of the plane passing through the points (x1, y1, z1), (x2, y2,z2) and (x3, y3, z3) is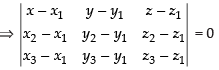
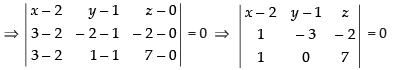
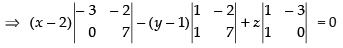
⇒ (x – 2) (– 21) – (y –1)(7 + 2) + z(3) = 0
⇒ – 21(x –2) – 9(y – 1) + 3z = 0
⇒ – 21x + 42 – 9y + 9 + 3z = 0
⇒ – 21x – 9y + 3z + 51 = 0 ⇒ 7x + 3y – z – 17 = 0
Hence, the required equation is 7x + 3y – z – 17 = 0.
Q.11. Find the equations of the two lines through the origin which intersect the line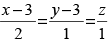 at angles of π/3 each.
at angles of π/3 each.
Ans.
Any point on the given line is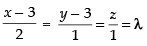
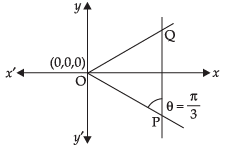 ⇒ x = 2λ + 3, y = λ + 3 and z = λ
⇒ x = 2λ + 3, y = λ + 3 and z = λ
Let it be the coordinates of P
∴ Direction ratios of OP are
(2λ + 3 – 0), (λ + 3 – 0) and (λ – 0) ⇒ 2λ + 3, λ + 3, λ
But the direction ratios of the line PQ are 2, 1, 1
∴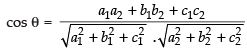
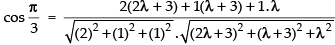
⇒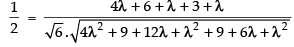
⇒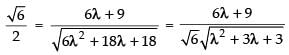
⇒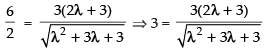
⇒
⇒ λ2 + 3λ + 3 = 4λ2 + 9 + 12λ (Squaring both sides)
⇒ 3λ2 + 9λ + 6 = 0 ⇒ λ2 + 3λ + 2 = 0
⇒ (λ + 1)(λ + 2) = 0
∴ λ = – 1, λ = – 2
∴ Direction ratios are [2(– 1) + 3, – 1 + 3, – 1] i.e., 1, 2, – 1 when λ = – 1 and [2(– 2) + 3, – 2 + 3, – 2] i.e., – 1, 1, – 2 when l = – 2.
Hence, the required equations are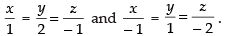
Q.12. Find the angle between the lines whose direction cosines are given by the equations l + m + n = 0, l2 + m2 – n2 = 0.
Ans.
The given equations are
l + m + n = 0 ...(i)
l2 + m2 – n2 = 0 ...(ii)
From equation (i) n = – (l + m)
Putting the value of n in eq. (ii) we get
l2 + m2 + [– (l + m)2] = 0
⇒ l2 + m2 – l2 – m2 – 2lm = 0
⇒ – 2lm = 0
⇒ lm = 0 ⇒ (– m – n)m = 0 [∵ l = – m – n]
⇒ (m + n)m = 0 ⇒ m = 0 or m = – n
⇒ l = 0 or l = – n
∴ Direction cosines of the two lines are
0, – n, n and – n, 0, n ⇒ 0, -1, 1 and - 1, 0, 1
∴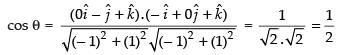
∴ θ = π/3
Hence, the required angle is π/3.
Q.13. If a variable line in two adjacent positions has direction cosines l, m, n and l + δl, m + δm, n + δn, show that the small angle δθ between the two positions is given by δθ2 = δl2 + δm2 + δn2
Ans.
Given that l, m, n and l + δl, m + δm, n + δn, are the direction cosines of a variable line in two positions
∴ l2 + m2 + n2 = 1 ...(i)
and (l + δl)2 + (m + δm)2 + (n + δn)2 = 1 ...(ii)
⇒ l2 + δl2 + 2l.δl + m2 + δm2 + 2m.δm + n2 + δn2 + 2n.δn = 1
⇒ (l2 + m2 + n2) + (δl2 + δm2 + δn2) + 2(l.δl + m.δm + n.δn) = 1
⇒ 1 + (δl2 + δm2 + δn2) + 2(l.δl + m.δm + n.δn) = 1
Let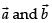 be the unit vectors along a line with d’cosines l, m, n and
be the unit vectors along a line with d’cosines l, m, n and
(l + δl), (m + δm), (n + δn).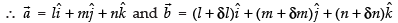
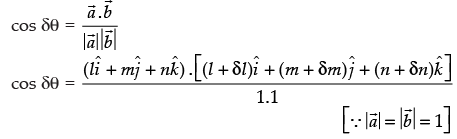
⇒ cos δθ = l(l + δl) + m(m + δm) + n(n + δn)
⇒ cos δθ = l2 + l.δl + m2 + m.δm + n2 + n.δn
⇒ cos δθ = (l2 + m2 + n2) + (l.δl + m.δm + n.δn)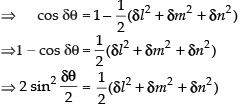
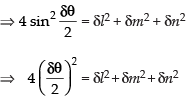
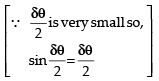
⇒ (δq)2 = δl2 + δm2 + δn2 Hence proved.
Q.14. O is the origin and A is (a, b, c).Find the direction cosines of the line OA and the equation of plane through A at right angle to OA
Ans.
We have A(a, b, c) and O(0, 0, 0)
∴ direction ratios of OA = a – 0, b – 0, c – 0
= a, b, c
∴ direction cosines of line OA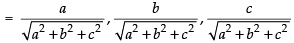
Now direction ratios of the normal to the plane are (a, b, c).
∴ Equation of the plane passing through the point
A(a, b, c) is a(x – a) + b(y – b) + c(z – c) = 0
⇒ ax – a2 + by – b2 + cz – c2 = 0
⇒ ax + by + cz = a2 + b2 + c2
Hence, the required equation is ax + by + cz = a2 + b2 + c2.
Q.15. Two systems of rectangular axis have the same origin. If a plane cuts them at distances a, b, c and a′, b′, c′, respectively, from the origin, prove that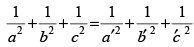
Ans.
Let OX, OY, OZ and ox, oy, oz be two rectangular systems
∴ Equations of two planes are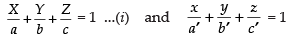 ...(ii)
...(ii)
Length of perpendicular from origin to plane (i) is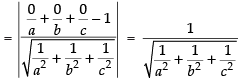
Length of perpendicular from origin to plane (ii)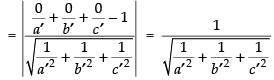
As per the condition of the question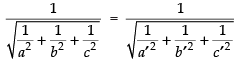
Hence,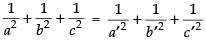
Long Answer Type Questions
Q.16. Find the foot of perpendicular from the point (2,3,–8) to the line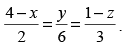 Also, find the perpendicular distance from the given point
Also, find the perpendicular distance from the given point
to the line.
Ans.
Given that: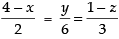 is the equation of line
is the equation of line
⇒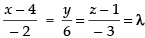
∴ Coordinates of any point Q on the line are
x = – 2λ + 4, y = 6λ and z = – 3λ + 1
and the given point is P(2, 3, – 8)
Direction ratios of PQ are – 2λ + 4 – 2, 6λ – 3, – 3λ +1 + 8
i.e., – 2λ + 2, 6λ – 3, – 3l + 9
and the D’ratios of the given line are – 2, 6, – 3.
If PQ ⊥ line
then – 2(– 2λ + 2) + 6(6λ – 3) – 3(– 3λ + 9) = 0
⇒ 4λ – 4 + 36λ – 18 + 9λ – 27 = 0
⇒ 49λ – 49 = 0
⇒ λ = 1
∴ The foot of the perpendicular is – 2(1) + 4, 6(1), – 3(1) + 1
i.e., 2, 6, – 2
Now, distance PQ =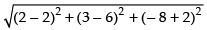
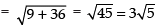
Hence, the required coordinates of the foot of perpendicular are 2, 6, – 2 and
the required distance is 3√5 units.
Q.17. Find the distance of a point (2,4,–1) from the line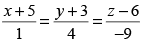
Ans.
The given equation of line is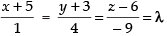 and any point P(2, 4, – 1)
and any point P(2, 4, – 1)
Let Q be any point on the given line
∴ Coordinates of Q are x = λ – 5, y = 4λ – 3, z = – 9λ + 6
D’ratios of PQ are λ – 5 – 2, 4λ – 3 – 4, – 9λ + 6 + 1
i.e., λ – 7, 4λ – 7, – 9λ + 7
and the d’ratios of the line are 1, 4, – 9
If 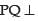 line then
line then
1(λ - 7) + 4(4λ - 7) - 9(- 9λ + 7)
= 0 λ - 7 + 16λ - 28 + 81λ - 63 = 0
⇒ 98λ – 98 = 0 ∴ λ = 1
So, the coordinates of Q are 1 – 5, 4 × 1 – 3, – 9 × 1 + 6
i.e., – 4, 1, – 3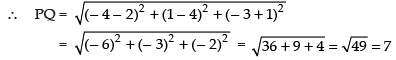
Hence, the required distance is 7 units.
Q.18. Find the length and the foot of perpendicular from the point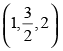 to the plane 2x – 2y + 4z + 5 = 0.
to the plane 2x – 2y + 4z + 5 = 0.
Ans.
Given plane is 2x – 2y + 4z + 5 = 0 and given point is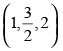
D’ratios of the normal to the plane are 2, – 2, 4
So, the equation of the line passing through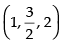
and whose d’ratios are equal to the d’ratios of the normal to the plane
i.e., 2, – 2, 4 is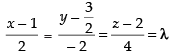
∴ Any point in the plane is 2λ + 1,- 2λ +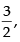 4λ + 2
4λ + 2
Since, the point lies in the plane, then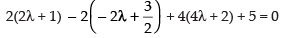
⇒ 4λ + 2 + 4λ - 3 + 16λ + 8 + 5 = 0
⇒ 24λ + 12 = 0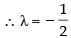
So, the coordinates of the point in the plane are
Hence, the foot of the perpendicular is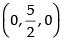 and the
and the
required length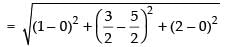
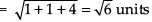
Q.19. Find the equations of the line passing through the point (3,0,1) and parallel to the planes x + 2y = 0 and 3y – z = 0.
Ans.
Given point is (3, 0, 1) and the equation of planes are
x + 2y = 0 ...(i)
and 3y – z = 0 ...(ii)
Equation of any line l passing through (3, 0, 1) is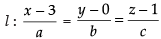
Direction ratios of the normal to plane (i) and plane (ii) are
(1, 2, 0) and (0, 3, – 1) Since the line is parallel to both the planes.
∴ 1.a + 2.b + 0.c = 0 ⇒ a + 2b + 0c = 0
and 0.a + 3.b – 1.c = 0 ⇒ 0.a + 3b - c = 0
So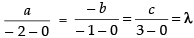
∴ a = – 2λ, b = λ, c = 3λ
So, the equation of line is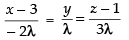
Hence, the required equation is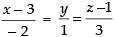
or in vector form is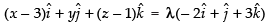
Q.20. Find the equation of the plane through the points (2,1,–1) and (–1,3,4), and perpendicular to the plane x – 2y + 4z = 10.
Ans.
Equation of the plane passing through two points (x1, y1, z1) and (x2, y2, z2) with its normal’s d’ratios is a
(x – x1) + b(y – y1) + c(z – z1) = 0 ..(i)
If the plane is passing through the given points (2, 1, – 1) and
(– 1, 3, 4) then
a(x2 – x1) + b(y2 – y1) + c(z2 – z1) = 0
⇒ a(– 1 – 2) + b(3 – 1) + c(4 + 1) = 0
⇒ – 3a + 2b + 5c = 0 ...(ii)
Since the required plane is perpendicular to the given plane
x – 2y + 4z = 10, then
1.a – 2.b + 4.c = 10 ...(iii)
Solving (ii) and (iii) we get,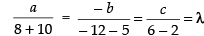
a = 18λ, b = 17λ, c = 4λ
Hence, the required plane is
18λ(x – 2) + 17λ(y – 1) + 4λ(z + 1) = 0
⇒ 18x – 36 + 17y – 17 + 4z + 4 = 0
⇒ 18x + 17y + 4z – 49 = 0
Q.21. Find the shortest distance between the lines given by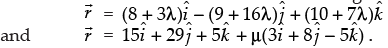
Ans.
Given equations of lines are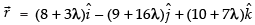 ...(i)
...(i)
and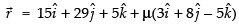 ...(ii)
...(ii)
Equation (i) can be re-written as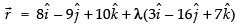 ...(iii)
...(iii)
Here,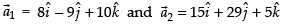
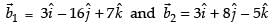
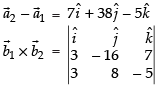
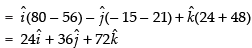
∴ Shortest distance, SD =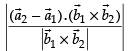

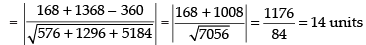
Hence, the required distance is 14 units.
Q.22. Find the equation of the plane which is perpendicular to the plane 5x + 3y + 6z + 8 = 0 and which contains the line of intersection of the planes x + 2y + 3z – 4 = 0 and 2x + y – z + 5 = 0.
Ans.
The given planes are
P1 : 5x + 3y + 6z + 8 = 0
P2 : x + 2y + 3z – 4 = 0
P3 : 2x + y – z + 5 = 0
Equation of the plane passing through the line of intersection of P2 and P3 is (x + 2y + 3z – 4) + λ(2x + y – z + 5) = 0
⇒ (1 + 2λ)x + (2 + λ)y + (3 – λ)z – 4 + 5λ = 0 ...(i)
Plane (i) is perpendicular to P1, then
5(1 + 2λ) + 3(2 + λ) + 6(3 – λ) = 0
⇒ 5 + 10λ + 6 + 3λ + 18 – 6λ = 0
⇒ 7λ + 29 = 0
∴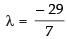
Putting the value of λ in eq. (i), we get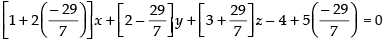
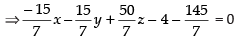
⇒ – 15x – 15y + 50z – 28 – 145 = 0
⇒ – 15x – 15y + 50z – 173 = 0
⇒ 51x + 15y – 50z + 173 = 0
Q.23. The plane ax + by = 0 is rotated about its line of intersection with the plane z = 0 through an angle α. Prove that the equation of the plane in its new position is ax + by ±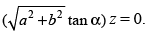
Ans.
Given planes are:
ax + by = 0 ...(i)
z = 0 ...(ii)
Equation of any plane passing through the line of intersection of plane (i) and (ii) is
(ax + by) + kz = 0 ⇒ ax + by + kz = 0 ...(iii)
Dividing both sides by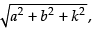 we get
we get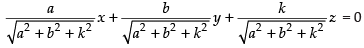
∴ Direction cosines of the normal to the plane are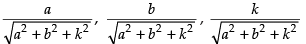
and the direction cosines of the plane (i) are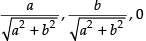
Since, α is the angle between the planes (i) and (iii), we get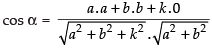
⇒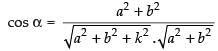
⇒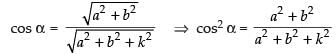
⇒ (a2 + b2 + k2) cos2 α = a2 + b2
⇒ a2 cos2 α + b2 cos2 α + k2 cos2 α = a2 + b2
⇒ k2 cos2 α = a2 – a2 cos2 α + b2 – b2 cos2 α
⇒ k2 cos2 α = a2(1 – cos2 α) + b2(1 – cos2 α)
⇒ k2 cos2 α = a2 sin2 α + b2 sin2 α
⇒ k2 cos2 α = (a2 + b2) sin2 α
⇒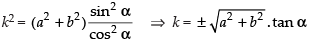
Putting the value of k in eq. (iii) we get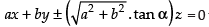 which is the required equation of plane.
which is the required equation of plane.
Hence proved.
Q.24. Find the equation of the plane through the intersection of the planes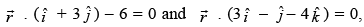 whose perpendicular distance from origin is unity.
whose perpendicular distance from origin is unity.
Ans.
Given planes are;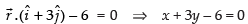 ...(i)
...(i)
and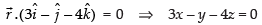 ...(ii)
...(ii)
Equation of the plane passing through the line of intersection of plane (i) and (ii) is
(x + 3y – 6) + k(3x – y – 4z) = 0 ...(iii)
(1 + 3k)x + (3 – k)y – 4kz – 6 = 0
Perpendicular distance from origin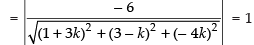
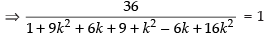 [Squaring both sides]
[Squaring both sides]
⇒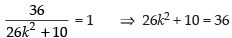
⇒ 26k2 = 26
⇒ k2 = 1
∴ k = ± 1
Putting the value of k in eq. (iii) we get,
(x + 3y - 6) ± (3x - y - 4z) = 0
⇒ x + 3y - 6 + 3x - y - 4z = 0 and x + 3y - 6 - 3x + y + 4z = 0
⇒ 4x + 2y - 4z - 6 = 0 and - 2x + 4y + 4z - 6 = 0
Hence, the required equations are:
4x + 2y - 4z - 6 = 0 and - 2x + 4y + 4z - 6 = 0.
Q.25. Show that the points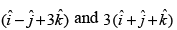 are equidistant from the plane
are equidistant from the plane 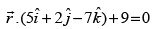 and lies on opposite side of it.
and lies on opposite side of it.
Ans.
Given points are and the plane
and the plane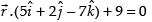
Perpendicular distance of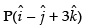 from the plane
from the plane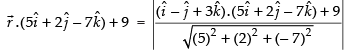
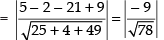
and perpendicular distance of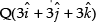 from the plane
from the plane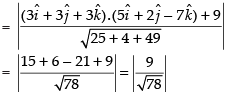
Hence, the two points are equidistant from the given plane. Opposite sign shows that they lie on either side of the plane.
Q.26. 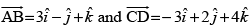 are two vectors. The position vectors of the points A and C are
are two vectors. The position vectors of the points A and C are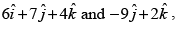 respectively. Find the position vector of a point P on the line AB and a point Q on the line CD such that
respectively. Find the position vector of a point P on the line AB and a point Q on the line CD such that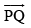 is perpendicular to
is perpendicular to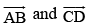 both.
both.
Ans.
Position vector of A is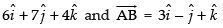
So, equation of any line passing through A and parallel to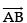
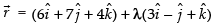 ...(i)
...(i)
Now any point P on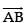 = (6 + 3λ, 7 – λ, 4 + λ)
= (6 + 3λ, 7 – λ, 4 + λ)
Similarly, position vector of C is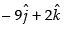
and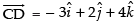
So, equation of any line passing through C and parallel to 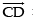 is
is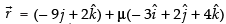 ...(ii)
...(ii)
Any point Q on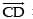 = (– 3μ, – 9 + 2μ, 2 + 4μ)
= (– 3μ, – 9 + 2μ, 2 + 4μ)
d’ratios of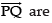
(6 + 3λ + 3μ, 7 – λ + 9 – 2μ, 4 + λ – 2 – 4μ)
⇒ (6 + 3λ + 3μ), (16 – λ – 2μ), (2 + λ – 4μ)
Now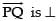 to eq. (i),then
to eq. (i),then
3(6 + 3λ + 3μ) – 1(16 – λ – 2μ) + 1(2 + λ – 4μ) = 0
⇒ 18 + 9λ + 9μ – 16 + λ + 2μ + 2 + λ – 4μ = 0
⇒ 11λ + 7μ + 4 = 0 ...(iii)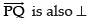 to eq. (ii), then
to eq. (ii), then
- 3(6 + 3λ + 3μ) + 2(16 - λ - 2μ) + 4(2 + λ - 4μ) = 0
⇒ - 18 - 9λ - 9μ + 32 - 2λ - 4μ + 8 + 4λ - 16μ = 0
⇒ – 7λ – 29μ + 22 = 0
⇒ 7λ + 29μ – 22 = 0 ...(iv)
Solving eq. (iii) and (iv) we get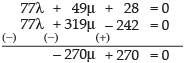
∴ μ = 1
Now using μ = 1 in eq. (iv) we get
7λ + 29 – 22 = 0
⇒ λ = – 1
∴ Position vector of P = [6 + 3(– 1), 7 + 1, 4 – 1] = (3, 8, 3)
and position vector of Q = [– 3(1), –9 + 2(1), 2 + 4(1)] = (– 3, –7, 6)
Hence, the position vectors of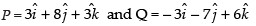
Q.27. Show that the straight lines whose direction cosines are given by 2l + 2m – n = 0 and mn + nl + lm = 0 are at right angles.
Ans.
Given that 2l + 2m – n = 0 ...(i)
and mn + nl + lm = 0 ...(ii)
Eliminating m from eq. (i) and (ii) we get,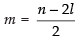 [from (i)]
[from (i)]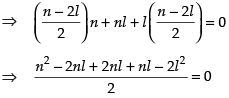
⇒ n2 + nl – 2l2 = 0
⇒ n2 + 2nl – nl – 2l2 = 0
⇒ n(n + 2l) – l(n + 2l) = 0
⇒ (n – l)(n + 2l) = 0
⇒ n = – 2l and n = l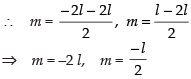
Therefore, the direction ratios are proportional to l, – 2l, –2l
and l,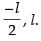
⇒ 1, – 2, – 2 and 2, – 1, 2
If the two lines are perpendicular to each other then 1(2) – 2(– 1) – 2 × 2 = 0
2 + 2 – 4 = 0
0 = 0
Hence, the two lines are perpendicular.
Q.28. If l1, m1, n1; l2, m2, n2; l3, m3, n3 are the direction cosines of three mutually perpendicular lines, prove that the line whose direction cosines are proportional to l1 + l2 + l3, m1 + m2 + m3, n1 + n2 + n3 makes equal angles with them.
Ans.
Let are such that
are such that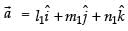
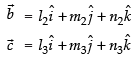
and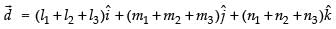
Since the given d’cosines are mutually perpendicular then
l1l2 + m1m2 + n1n2 = 0
l2l3 + m2m3 + n2n3 = 0
l1l3 + m1m3 + n1n3 = 0
Let α , β and γ be the angles between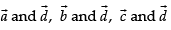
∴ cos α = l1(l1 + l2 + l3) + m1(m1 + m2 + m3) + n1(n1 + n2 + n3)
= l12 + l1l2 + l1l3 + m12 + m1m2 + m1m3 + n12+ n1n2 + n1n3
= (l12 + m12+n12) + (l1l2 + m1m2 + n1n2) + (l1l3 + m1m3 + n1n3)
= 1 + 0 + 0 = 1
∴ cos β = l2(l1 + l2 + l3) + m2(m1 + m2 + m3) + n2(n1 + n2 + n3)
= l1l2 + l22+ l2 l3 + m1m2 + m22 + m2 m3 + n1n2 + n22 + n2 n3
= (l22 + m22+n22) + (l1l2 + m1m2 + n1n2) + (l2l3 + m2m3 + n2n3)
= 1 + 0 + 0 = 1
Similarly,
∴ cos γ = l3(l1 + l2 + l3) + m3(m1 + m2 + m3) + n3(n1 + n2 + n3)
= l1l3 + l2 l3 + l32+ m1m3 + m2 m3 + m32 + n1n3 + n2 n3 + n32
= (l32 + m32+n32) + (l1l3 + m1m3 + n1n3) + (l2l3 + m2m3 + n2n3)
= 1 + 0 + 0 = 1
∴ cos α = cos β = cos γ = 1
⇒ α = β = γ which is the required result.
Objective Type Questions
Q.29. Distance of the point (α,β,γ) from y-axis is
(a) β
(b)
(c)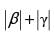
(d)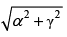
Ans. (d)
Solution.
The given point is (α, β, γ)
Any point on y-axis = (0, β, 0)
∴ Required distance =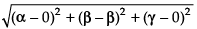
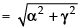
Hence, the correct option is (d).
Q.30. If the directions cosines of a line are k,k,k, then
(a) k > 0
(b) 0 < k < 1
(c) k = 1
(d)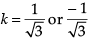
Ans. (d)
Solution.
If l , m, n are the direction cosines of a line, then
l2 + m2 + n2 = 1
So, k2 + k2 + k2 = 1
⇒ 3k2 = 1 ⇒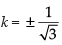
Hence, the correct option is (d).
Q.31. The distance of the plane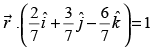 from the origin is
from the origin is
(a) 1
(b) 7
(c) 1/7
(d) None of these
Ans. (a)
Solution.
Given that: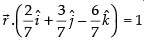
So, the distance of the given plane from the origin is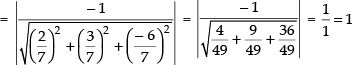
Hence, the correct option is (a).
Q.32. The sine of the angle between the straight line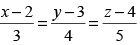 and the plane 2x – 2y + z = 5 is
and the plane 2x – 2y + z = 5 is
(a)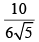
(b)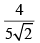
(c)
(d)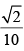
Ans. (d)
Solution.
Given that: l :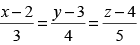
and P : 2x – 2y + z = 5
d’ratios of the line are 3, 4, 5
and d’ratios of the normal to the plane are 2, – 2, 1
∴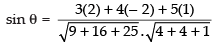
⇒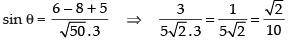
Hence, the correct option is (d).
Q.33. The reflection of the point (α,β,γ) in the xy– plane is
(a) (α,β,0)
(b) (0,0,γ)
(c) (–α,–β,γ)
(d) (α,β,–γ)
Ans. (d)
Solution.
Reflection of point (α, β, γ) in xy-plane is (a,b,–g).
Hence, the correct option is (d).
Q.34. The area of the quadrilateral ABCD, where A(0,4,1), B (2, 3, –1), C(4, 5, 0) and D (2, 6, 2), is equal to
(a) 9 sq. units
(b) 18 sq. units
(c) 27 sq. units
(d) 81 sq. units
Ans. (a)
Solution.
Given points are
A(0, 4, 1), B(2,3,– 1), C(4, 5, 0) and D(2,6,2)
d’ratios of AB = 2,–1 –2
and d’ratios of DC = 2,–1,–2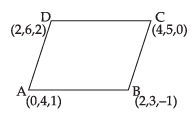 ∴ AB ║DC
∴ AB ║DC
Similarly, d’ratios of AD = 2, 2, 1
and d’ratios of BC = 2, 2, 1
∴ AD ║BC
So 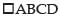 is a parallelogram.
is a parallelogram.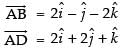
∴ Area of parallelogram ABCD =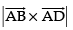
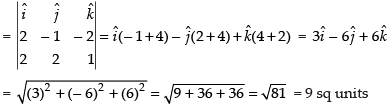
Hence, the correct option is (a).
Q.35. The locus represented by xy + yz = 0 is
(a) A pair of perpendicular lines
(b) A pair of parallel lines
(c) A pair of parallel planes
(d) A pair of perpendicular planes
Ans. (d)
Solution.
Given that:
xy + yz = 0
y.(x + z) = 0
y = 0 or x + z = 0
Here y = 0 is one plane and x + z = 0 is another plane. So, it is a pair of perpendicular planes.
Hence, the correct option is (d).
Q.36. The plane 2x – 3y + 6z – 11 = 0 makes an angle sin–1(α) with x-axis. The value of α is equal to
(a) √3/2
(b) √2/3
(c) 2/7
(d) 3/7
Ans. (c)
Solution.
Direction ratios of the normal to the plane 2x – 3y + 6z – 11 = 0 are 2, – 3, 6
Direction ratios of x-axis are 1, 0, 0
∴ angle between plane and line is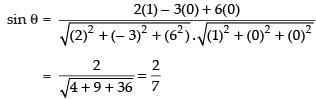
Hence, the correct option is (c).
Fill in the blanks
Q.37. A plane passes through the points (2,0,0) (0,3,0) and (0,0,4). The equation of plane is _______.
Ans.
Given points are (2, 0, 0), (0, 3, 0) and (0, 0, 4).
So, the intercepts cut by the plane on the axes are 2, 3, 4
Equation of the plane (intercept form) is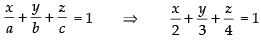
Hence, the equation of plane is
Q.38. The direction cosines of the vector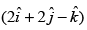 are ______.
are ______.
Ans.
Let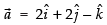
direction ratios of 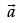 are 2,2,-1
are 2,2,-1
So, the direction cosines are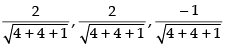
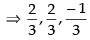
Hence, the direction cosines of the given vector are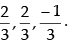
Q.39. The vector equation of the line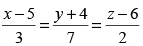 is _______.
is _______.
Ans.
The given equation is
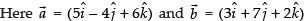
Equation of the line is
Hence, the vector equation of the given line is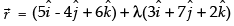
Q.40. The vector equation of the line through the points (3,4,–7) and (1,–1,6) is _______.
Ans.
Given the points (3, 4, –7) and (1, –1, 6)
Equation of the line is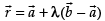
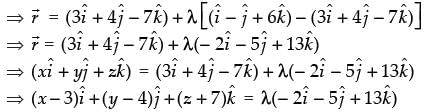
Hence, the vector equation of the line is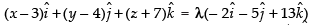
Q.41. The cartesian equation of the plane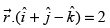 is ________.
is ________.
Ans.
Given equation is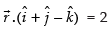
⇒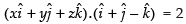
⇒ x + y – z = 2
Hence, the Cartesian equation of the plane is x + y – z = 2.
State True or False for the statements
Q.42. The unit vector normal to the plane x + 2y + 3z – 6 = 0 is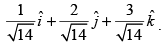
Ans.
Given plane is x + 2y + 3z – 6 = 0
Vector normal to the plane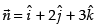
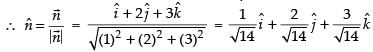
Hence, the given statement is ‘true’
Q.43. The intercepts made by the plane 2x – 3y + 5z +4 = 0 on the co-ordinate axis are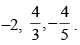
Ans.
Equation of the plane is 2x – 3y + 5z + 4 = 0
⇒ 2x – 3y + 5z = – 4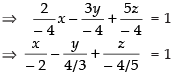
So, the required intercepts are
Hence, the given statement is ‘true’.
Q.44. The angle between the line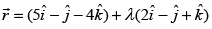 and the plane
and the plane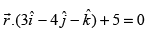 is
is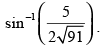
Ans.
Equation of line is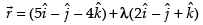 and the equation of the plane is
and the equation of the plane is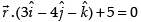
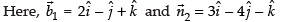
∴
⇒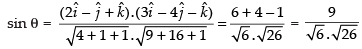
⇒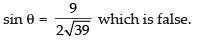
Hence, the given statement is ‘false’.
Q.45. The angle between the planes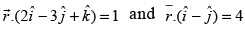 is
is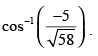
Ans.
The given planes are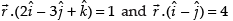
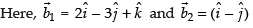
So,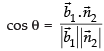
⇒
∴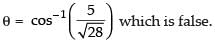
Hence, the given statement is ‘false’.
Q.46. The line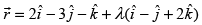 lies in the plane
lies in the plane 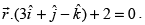
Ans.
Direction ratios of the line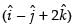
Direction ratios of the normal to the plane are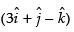
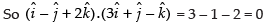
Therefore, the line is parallel to the plane.
Now point through which the line is passing 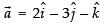
If line lies in the plane then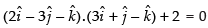
6 – 3 + 1 + 2 ≠ 0
So, the line does not lie in the plane.
Hence, the given statement is ‘false’.
Q.47. The vector equation of the line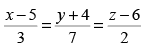 is
is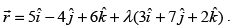
Ans.
The Cartesian form of the equation is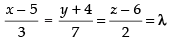
∴ Here x1 = 5, y1 = – 4, z1 = 6, a = 3, b = 7, c = 2
So, the vector equation is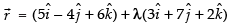
Hence, the given statement is ‘true’.
Q.48. The equation of a line, which is parallel to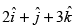 and which passes through the point (5,–2,4), is
and which passes through the point (5,–2,4), is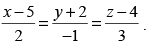
Ans.
Here, x1 = 5, y1 = – 2, z1 = 4; a = 2, b = 1, c = 3
We know that the equation of line is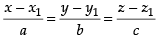
⇒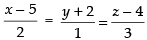
Hence, the given statement is ‘false’.
Q.49. If the foot of perpendicular drawn from the origin to a plane is (5, – 3, – 2), then the equation of plane is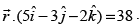
Ans.
The given equation of the plane is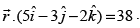
If the foot of the perpendicular to this plane is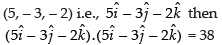
⇒ 25 + 9 + 4 = 38
38 = 38 (satisfied)
Hence, the given statement is ‘true’.
|
172 videos|503 docs|154 tests
|
FAQs on NCERT Exemplar: Three Dimensional Geometry - Mathematics (Maths) for JEE Main & Advanced
| 1. How do you find the distance between two points in three-dimensional space? |  |
| 2. What are the coordinates of the midpoint of a line segment in three-dimensional space? |  |
| 3. How do you determine if two lines in three-dimensional space are parallel or perpendicular? |  |
| 4. How can you find the equation of a plane passing through a given point with a given normal vector in three-dimensional space? |  |
| 5. What is the angle between two planes in three-dimensional space? |  |




















