NCERT Solution - Relations and Functions (Ex - 2.1) | Additional Study Material for JEE PDF Download
NCERT QUESTION
(Ex - 2.1)
Ques 1: If 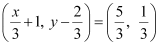 , find the values of x and y.
, find the values of x and y.
Ans: It is given that  .
.
Since the ordered pairs are equal, the corresponding elements will also be equal.
Therefore, 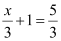 and
and 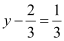 .
.
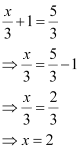
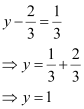
∴ x = 2 and y = 1
Ques 2: If the set A has 3 elements and the set B = {3, 4, 5}, then find the number of elements in (A × B)?
Ans: It is given that set A has 3 elements and the elements of set B are 3, 4, and 5.
⇒ Number of elements in set B = 3
Number of elements in (A × B)
= (Number of elements in A) × (Number of elements in B)
= 3 × 3 = 9
Thus, the number of elements in (A × B) is 9.
Ques 3: If G = {7, 8} and H = {5, 4, 2}, find G × H and H × G.
Ans: G = {7, 8} and H = {5, 4, 2}
We know that the Cartesian product P × Q of two non-empty sets P and Q is defined as
P × Q = {(p, q): p∈ P, q ∈ Q}
∴G × H = {(7, 5), (7, 4), (7, 2), (8, 5), (8, 4), (8, 2)}
H × G = {(5, 7), (5, 8), (4, 7), (4, 8), (2, 7), (2, 8)}
Ques 4: State whether each of the following statement are true or false. If the statement is false, rewrite the given statement correctly.
(i) If P = {m, n} and Q = {n, m}, then P × Q = {(m, n), (n, m)}.
(ii) If A and B are non-empty sets, then A × B is a non-empty set of ordered pairs (x, y) such that x ∈ A and y ∈ B.
(iii) If A = {1, 2}, B = {3, 4}, then A × (B ∩ Φ) = Φ.
Ans: (i) False
If P = {m, n} and Q = {n, m}, then
P × Q = {(m, m), (m, n), (n, m), (n, n)}
(ii) True
(iii) True
Ques 5: If A = {–1, 1}, find A × A × A.
Ans: It is known that for any non-empty set A, A × A × A is defined as
A × A × A = {(a, b, c): a, b, c ∈ A}
It is given that A = {–1, 1}
∴ A × A × A = {(–1, –1, –1), (–1, –1, 1), (–1, 1, –1), (–1, 1, 1),
(1, –1, –1), (1, –1, 1), (1, 1, –1), (1, 1, 1)}
Ques 6: If A × B = {(a, x), (a, y), (b, x), (b, y)}. Find A and B.
Ans: It is given that A × B = {(a, x), (a, y), (b, x), (b, y)}
We know that the Cartesian product of two non-empty sets P and Q is defined as P × Q = {(p, q): p ∈ P, q ∈ Q}
∴ A is the set of all first elements and B is the set of all second elements.
Thus, A = {a, b} and B = {x, y}
Ques 7: Let A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} and D = {5, 6, 7, 8}. Verify that
(i) A × (B ∩ C) = (A × B) ∩ (A × C)
(ii) A × C is a subset of B × D
Ans: (i) To verify: A × (B ∩ C) = (A × B) ∩ (A × C)
We have B ∩ C = {1, 2, 3, 4} ∩ {5, 6} = Φ
∴L.H.S. = A × (B ∩ C) = A × Φ = Φ
A × B = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4)}
A × C = {(1, 5), (1, 6), (2, 5), (2, 6)}
∴ R.H.S. = (A × B) ∩ (A × C) = Φ
∴L.H.S. = R.H.S
Hence, A × (B ∩ C) = (A × B) ∩ (A × C)
(ii) To verify: A × C is a subset of B × D
A × C = {(1, 5), (1, 6), (2, 5), (2, 6)}
B × D = {(1, 5), (1, 6), (1, 7), (1, 8), (2, 5), (2, 6), (2, 7), (2, 8), (3, 5), (3, 6), (3, 7), (3, 8), (4, 5), (4, 6), (4, 7), (4, 8)}
We can observe that all the elements of set A × C are the elements of set B × D.
Therefore, A × C is a subset of B × D.
Ques 8: Let A = {1, 2} and B = {3, 4}. Write A × B. How many subsets will A × B have? List them.
Ans: A = {1, 2} and B = {3, 4}
∴A × B = {(1, 3), (1, 4), (2, 3), (2, 4)}
⇒ n(A × B) = 4
We know that if C is a set with n(C) = m, then n[P(C)] = 2m.
Therefore, the set A × B has 24 = 16 subsets. These are
Φ, {(1, 3)}, {(1, 4)}, {(2, 3)}, {(2, 4)}, {(1, 3), (1, 4)}, {(1, 3), (2, 3)},
{(1, 3), (2, 4)}, {(1, 4), (2, 3)}, {(1, 4), (2, 4)}, {(2, 3), (2, 4)},
{(1, 3), (1, 4), (2, 3)}, {(1, 3), (1, 4), (2, 4)}, {(1, 3), (2, 3), (2, 4)},
{(1, 4), (2, 3), (2, 4)}, {(1, 3), (1, 4), (2, 3), (2, 4)}
Ques 9: Let A and B be two sets such that n(A) = 3 and n (B) = 2. If (x, 1), (y, 2), (z, 1) are in A × B, find A and B, where x, y and z are distinct elements.
Ans: It is given that n(A) = 3 and n(B) = 2; and (x, 1), (y, 2), (z, 1) are in A × B.
We know that A = Set of first elements of the ordered pair elements of A × B
B = Set of second elements of the ordered pair elements of A × B.
∴ x, y, and z are the elements of A; and 1 and 2 are the elements of B.
Since n(A) = 3 and n(B) = 2, it is clear that A = {x, y, z} and B = {1, 2}.
Ques 10: The Cartesian product A × A has 9 elements among which are found (–1, 0) and (0, 1). Find the set A and the remaining elements of A × A.
Ans: We know that if n(A) = p and n(B) = q, then n(A × B) = pq.
∴ n(A × A) = n(A) × n(A)
It is given that n(A × A) = 9
∴ n(A) × n(A) = 9
⇒ n(A) = 3
The ordered pairs (–1, 0) and (0, 1) are two of the nine elements of A × A.
We know that A × A = {(a, a): a ∈ A}. Therefore, –1, 0, and 1 are elements of A.
Since n(A) = 3, it is clear that A = {–1, 0, 1}.
The remaining elements of set A × A are (–1, –1), (–1, 1), (0, –1), (0, 0),
(1, –1), (1, 0), and (1, 1)
|
22 videos|163 docs|17 tests
|
FAQs on NCERT Solution - Relations and Functions (Ex - 2.1) - Additional Study Material for JEE
| 1. What are relations and functions in mathematics? |  |
| 2. How are relations and functions different from each other? |  |
| 3. What is the domain and range of a function? |  |
| 4. How can relations and functions be represented graphically? |  |
| 5. What are some real-life applications of relations and functions? |  |

















