NCERT Solutions (Exercise 1.4) - Relations and Functions - Class 12 PDF Download
RELATIONS AND FUNCTIONS
Q.1. Determine whether or not each of the definition of given below gives a binary operation.
In the event that * is not a binary operation, give justification for this.
(i) On Z+, define * by a * b = a − b
(ii) On Z+, define * by a * b = ab
(iii) On R, define * by a * b = ab2
(iv) On Z+, define * by a * b = |a − b|
(v) On Z+, define * by a * b = a
Ans.
(i) On Z+, * is defined by a * b = a − b.
It is not a binary operation
as the image of (1, 2) under * is 1 * 2 = 1 − 2 = −1 ∉ Z+
(ii) On Z+, * is defined by a * b = ab.
It is seen that for each a, b ∈ Z+, there is a unique element ab in Z+.
This means that * carries each pair (a, b) to a unique element a * b = ab in Z+.
Therefore, * is a binary operation.
(iii) On R, * is defined by a * b = ab2.
It is seen that for each a, b ∈ R, there is a unique element ab2 in R.
This means that * carries each pair (a, b) to a unique element a * b = ab2 in R.
Therefore, * is a binary operation. www
(iv) On Z+, * is defined by a * b = |a − b|.
It is seen that for each a, b ∈ Z+, there is a unique element |a − b| in Z+.
This means that * carries each pair (a, b) to a unique element a * b = |a − b| in Z+.
Therefore, * is a binary operation. www
(v) On Z+, * is defined by a * b = a.
It is seen that for each a, b ∈ Z+, there is a unique element a in Z+.
This means that * carries each pair (a, b) to a unique element a * b = a in Z+.
Therefore, * is a binary operation.
Q.2. For each binary operation * defined below, determine whether * is commutative or associative.
(i) On Z, define a * b = a − b
(ii) On Q, define a * b = ab + 1
(iii) On Q, define a * b = ab/2
(iv) On Z+, define a * b = 2ab
(v) On Z+, define a * b = ab
(vi) On R − {−1}, define ??∗?? = a/b +1
Ans.
(i) On Z, * is defined by a * b = a − b.
It can be observed that 1 * 2 = 1 − 2 = −1 and 2 * 1 = 2 − 1 = 1.
∴ 1 * 2 ≠ 2 * 1, where 1, 2 ∈ Z
Hence, the operation * is not commutative.
Also, we have
(1 * 2) * 3 = (1 − 2) * 3 = −1 * 3 = −1 − 3 = −4
1 * (2 * 3) = 1 * (2 − 3) = 1 * −1 = 1 − (−1) = 2
∴ (1 * 2) * 3 ≠ 1 * (2 * 3), where 1, 2, 3 ∈ Z
Hence, the operation * is not associative.
(ii) On Q, * is defined by a * b = ab + 1.
It is known that: ab = ba for all a, b ∈ Q
⇒ ab + 1 = ba + 1 for all a, b ∈ Q
⇒ a * b = a * b for all a, b ∈ Q
Therefore, the operation * is commutative.
It can be observed that
(1 * 2) * 3 = (1 × 2 + 1) * 3 = 3 * 3 = 3 × 3 + 1 = 10
1 * (2 * 3) = 1 * (2 × 3 + 1) = 1 * 7 = 1 × 7 + 1 = 8
∴ (1 * 2) * 3 ≠ 1 * (2 * 3), where 1, 2, 3 ∈ Q
Therefore, the operation * is not associative.
(iii) On Q, * is defined by a * b = ab/2
It is known that: ab = ba for all a, b ∈ Q
⇒ ab/2 = ba/2 for all a, b ∈ Q
⇒ a ∗ b = b ∗ a for all a, b ∈ Q
Therefore, the operation ∗ is commutative.
For all a, b, c ∈ Q, we have
∴ (a * b)*c = a*(b * c), where a,b,c ∈ Q
Therefore, the operation * is associative
(iv) On Z+, * is defined by a * b = 2ab.
It is known that: ab = ba for all a, b ∈ Z+
⇒ 2ab = 2ba for all a, b ∈ Z+
⇒ a * b = b * a for all a, b ∈ Z+
Therefore, the operation * is commutative.
It can be observed that
(1 ∗ 2) ∗ 3=21×2 ∗ 3 = 4 ∗ 3 = 24×3 = 212 and
1 ∗ (2 ∗ 3) = 1 ∗ 22×3 = 1 ∗ 26 = 1 ∗ 64 = 21×64 = 264
∴ (1 * 2) * 3 ≠ 1 * (2 * 3), where 1, 2, 3 ∈ Z+
Therefore, the operation * is not associative.
(v) On Z+, * is defined by a * b = ab.
It can be observed that
1 * 2 = 12 = 1 and 2 * 1 = 21 = 2
∴ 1 * 2 ≠ 2 * 1. where 1 .2 ∈ Z+
Therefore, the operation * is not commutative.
It can also be observed that
(2 * 3 ) * 4 = 23 * 4 = 8 * 4 = 84 = 212
and 2 * (3 * 4) = 2 * 34 = 2 * 81 = 281
∴ (2 * 3) * 4 ≠ 2 * (3 * 4), where 2, 3, 4 ∈ Z+
Therefore, the operation * is not associative.
(vi) On R, * − {−1} is defined by ??∗??= a/b + 1
It can be observed that
Therefore, the operation * is not commutative.
It can also be observed that
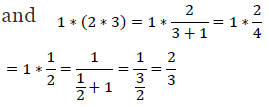
∴ (1 * 2) * 3 ≠ 1 * (2 * 3), where 1, 2, 3 ∈ R − {−1} Therefore, the operation * is not associative.
Q.3. Consider the binary operation ∧ on the set {1, 2, 3, 4, 5} defined by a ∧ b = min {a, b}. Write the operation table of the operation ∧.
Ans. The binary operation ∧ on the set {1, 2, 3, 4, 5} is defined as a ∧ b = min {a, b} for all a, b ∈ {1, 2, 3, 4, 5}. Thus, the operation table for the given operation ∧ can be given as:
∧ | 1 | 2 | 3 | 4 | 5 |
1 | 1 | 1 | 1 | 1 | 1 |
2 | 1 | 2 | 2 | 2 | 2 |
3 | 1 | 2 | 3 | 3 | 3 |
4 | 1 | 2 | 3 | 4 | 4 |
5 | 1 | 2 | 3 | 4 | 5 |
Q.4. Consider a binary operation * on the set {1, 2, 3, 4, 5} given by the following multiplication table.
(i) Compute (2 * 3) * 4 and 2 * (3 * 4)
(ii) Is * commutative?
(iii) Compute (2 * 3) * (4 * 5).
(Hint : use the following table)
* | 1 | 2 | 3 | 4 | 5 |
1 | 1 | 1 | 1 | 1 | 1 |
2 | 1 | 2 | 1 | 2 | 1 |
3 | 1 | 1 | 3 | 1 | 1 |
4 | 1 | 2 | 1 | 4 | 1 |
5 | 1 | 1 | 1 | 1 | 5 |
Ans.
(i) (2 * 3) * 4 = 1 * 4 = 1
2 * (3 * 4) = 2 * 1 = 1
(ii) For every a, b ∈ {1, 2, 3, 4, 5}, we have a * b = b * a. Therefore, the operation*is commutative.
(iii) (2 * 3) = 1 and (4 * 5) = 1
∴ (2 * 3) * (4 * 5) = 1 * 1 = 1
Q.5. Let *′ be the binary operation on the set {1, 2, 3, 4, 5} defined by a *′ b = H.C.F. of a and b. Is the operation *′ same as the operation * defined in Exercise 4 above? Justify your answer.
Ans.
The binary operation *′ on the set {1, 2, 3 4, 5} is defined as a *′ b = H.C.F of a and b.
The operation table for the operation *′ can be given as:
*' | 1 | 2 | 3 | 4 | 5 |
1 | 1 | 1 | 1 | 1 | 1 |
2 | 1 | 2 | 1 | 2 | 1 |
3 | 1 | 1 | 3 | 1 | 1 |
4 | 1 | 2 | 1 | 4 | 1 |
5 | 1 | 1 | 1 | 1 | 5 |
We observe that the operation tables for the operations * and *′ are the same.
Thus, the operation *′ is same as the operation*.
Q.6. Let * be the binary operation on N given by a * b = L.C.M. of a and b. Find
(i) 5 * 7, 20 * 16
(ii) Is * commutative?
(iii) Is * associative?
(iv) Find the identity of * in N
(v) Which elements of N are invertible for the operation *?
Ans.
The binary operation * on N is defined as a * b = L.C.M. of a and b.
(i) 5 * 7 = L.C.M. of 5 and 7 = 35
20 * 16 = L.C.M of 20 and 16 = 80
(ii) It is known that
L.C.M of a and b = L.C.M of b and a for all a, b ∈ N.
∴ a * b = b * a
Thus, the operation * is commutative.
(iii) For a, b, c ∈ N, we have
(a * b) * c = (L.C.M of a and b) * c = LCM of a, b, and c
a * (b * c) = a * (LCM of b and c) = L.C.M of a, b, and c
∴ (a * b) * c = a * (b * c)
Thus, the operation * is associative.
(iv) It is known that:
L.C.M. of a and 1 = a = L.C.M. 1 and a for all a ∈ N
⇒ a * 1 = a = 1 * a for all a ∈ N
Thus, 1 is the identity of * in N.
(v) An element a in N is invertible with respect to the operation * if there exists an element b in N, such that a * b = e = b * a.
Here, e = 1
This means that L.C.M of a and b = 1 = L.C.M of b and a
This case is possible only when a and b are equal to 1.
Thus, 1 is the only invertible element of N with respect to the operation *.
Q.7. Is * defined on the set {1, 2, 3, 4, 5} by a * b = L.C.M. of a and b a binary operation? Justify your answer.
Ans.
The operation * on the set A = {1, 2, 3, 4, 5} is defined as a * b = L.C.M. of a and b.
Then, the operation table for the given operation * can be given as:
* | 1 | 2 | 3 | 4 | 5 |
1 | 1 | 2 | 3 | 4 | 5 |
2 | 2 | 2 | 6 | 4 | 10 |
3 | 3 | 6 | 3 | 12 | 15 |
4 | 4 | 4 | 12 | 4 | 20 |
5 | 5 | 10 | 15 | 20 | 5 |
It can be observed from the obtained table that
3 * 2 = 2 * 3 = 6 ∉ A,
5 * 2 = 2 * 5 = 10 ∉ A,
3 * 4 = 4 * 3 = 12 ∉ A,
3 * 5 = 5 * 3 = 15 ∉ A,
4 * 5 = 5 * 4 = 20 ∉A
Hence, the given operation * is not a binary operation.
Q.8. Let * be the binary operation on N defined by a * b = H.C.F. of a and b. Is * commutative? Is * associative? Does there exist identity for this binary operation on N?
Ans. The binary operation * on N is defined as: a * b = H.C.F. of a and b It is known that H.C.F. of a and b = H.C.F. of b and a for all a, b ∈ N.
∴ a * b = b * a
Thus, the operation * is commutative.
For a, b, c ∈ N, we have
(a * b)* c = (H.C.F. of a and b) * c = H.C.F. of a, b and c
a *(b * c) = a *(H.C.F. of b and c) = H.C.F. of a, b, and c
∴ (a * b) * c = a * (b * c)
Thus, the operation * is associative.
Now, an element e ∈ N will be the identity for the operation * if a * e = a = e* a for all a ∈ N.
But this relation is not true for any a ∈ N.
Thus, the operation * does not have any identity in N.
Q.9. Let * be a binary operation on the set Q of rational numbers as follows:
(i) a * b = a − b
(ii) a * b = a2 + b2
(iii) a * b = a + ab
(iv) a * b = (a − b)2
(v) a * b= ab/4
(vi) a * b = ab2
Find which of the binary operations are commutative and which are associative.
Ans.
(i) On Q, the operation * is defined as a * b = a − b. It can be observed that:
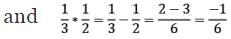
Thus, the operation * is not commutative. It can also be observed that
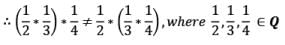
Thus the operation * is not associative.
(ii) On Q, the operation * is defined as a * b = a2 + b2.
For a, b ∈ Q. we have
a * b = a2 + b2 = b2 + a2 = b * a
∴ a * b = b * a
Thus, the operation * is commutative.
It can be observed that
(1 * 2) * 3 = (12 + 22) * 3 = (1 + 4) * 3 = 5 * 3 = 52 + 32 = 34 and
1 * ( 2 * 3 ) = 1 * (22 + 32 ) = 1 * (4 + 9) = 1 * 13 = 12 + 132 =170
∴ (1 * 2) * 3 ≠ 1 * (2 * 3), where 1, 2, 3 ∈ Q
Thus, the operation * is not associative.
(iii) On Q, the operation * is defined as a * b = a + ab.
It can be observed that
1 * 2 = 1 + 1 × 2 = 1 + 2 = 3
2 * 1 = 2 + 2 × 1 = 2 + 2 = 4
∴ 1 * 2 ≠ 2 * 1, where 1, 2 ∈ Q
Thus, the operation * is not commutative.
It can also be observed that
(1 * 2) * 3 = (1 + 1 × 2) * 3 = (1 + 2) * 3 = 3 * 3 = 3 + 3 × 3 = 3 + 9 = 12 and
1 * (2 * 3) = 1 * (2 + 2 × 3) = 1 * (2 + 6) = 1 * 8 = 1 + 1 × 8 =1 + 8 = 9
∴ (1 * 2) * 3 ≠ 1 * (2 * 3), where 1, 2, 3 ∈ Q
Thus, the operation * is not associative.
(iv) On Q, the operation * is defined by a * b = (a − b)2.
For a, b ∈ Q, we have
a * b = (a - b)2
b * a = (b - a)2 = [- (a - b)] 2 = (a - b)2
∴ a* b = b* a
Thus, the operation * is commutative.
It can be observed that
(1 * 2) * 3 = (1 - 2)2 * 3 = ( - 1) 2 * 3 = 1 * 3 = (1 - 3)2 = (- 2)2
and 1 * (2 * 3) = 1 * (2 - 3)2 = 1 * (- 1)2 = 1 * 1 = (1 - 1)2 = 0
∴ (1 * 2) * 3 ≠ 1 * (2 * 3), where 1, 2, 3 ∈ Q
Thus, the operation * is not associative.
(v) On Q, the operation * is defined as a * b = ab/4
For a, b ∈ Q, we have
a * b = ab/4 = ba/4 = b * a
∴ a * b = b * a
Thus, the operation * is commutative.
For a, b, c ∈ Q, we have
∴ (a * b) * c = a * (b * c), where a, b, c ∈ Q
Thus, the operation * is associative.
(vi) On Q, the operation * is defined as a * b = ab2
It can be observed that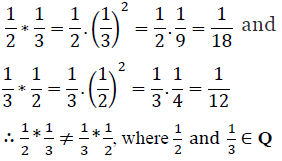
Thus, the operation * is not commutative.
It can also be observed that
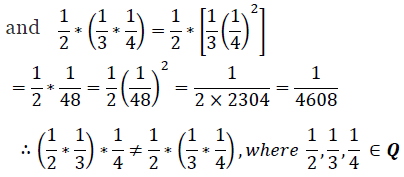
Thus, the operation * is not associative.
Hence, the operations defined in (ii), (iv), (v) are commutative and the operation defined in (v) is associative.
Q.10. Find which of the operations given above has identity.
Ans. An element e ∈ Q will be the identity element for the operation *
if a * e = a = e * a, for all a ∈ Q.
However, there is no such element e ∈ Q with respect to each of the six operations satisfying the above condition.
Thus, none of the six operations has identity.
Q.11. Let A = N × N and * be the binary operation on A defined by (a, b) * (c, d) = (a + c, b + d) Show that * is commutative and associative. Find the identity element for * on A, if any.
Ans. A = N × N and * is a binary operation on A and is defined by (a, b) * (c, d) = (a + c, b + d)
Let (a, b), (c, d) ∈ A
Then, a, b, c, d ∈ N
We have:
(a, b) * (c, d) = (a + c, b + d)
(c, d) * (a, b) = (c + a, d + b) = (a + c, b + d)
[Addition is commutative in the set of natural numbers]
∴ (a, b) * (c, d) = (c, d) * (a, b)
Therefore, the operation * is commutative.
Now, let (a, b), (c, d), (e, f) ∈ A
Then, a, b, c, d, e, f ∈ N
We have
[(a, b) ∗ (c, d)] ∗ (e, f) = (a + c, b + d) ∗ (e, f) = (a + c + e, b + d + f)
and (a, b) ∗ (c, d)] ∗ (e, f) ] = (a + c + e, b + d + f)
∴ [(a, b) ∗ (c, d)] ∗ (e, f) = (a, b) ∗ [(c, d) ∗ (e, f)]
Therefore, the operation * is associative.
Let an element e=(e1, e2)∈ A will be an identity element for the operation *
if a * e = a = e * a for all a=(a1, a2)∈ A
i.e.,(a1 + e1, a2 + e2) = (a1, a2) = (e1 + a1, e2 + a2)
Which is not true for any element in A.
Therefore, the operation * does not have any identity element.
Q.12. State whether the following statements are true or false. Justify.
(i) For an arbitrary binary operation * on a set N, a * a = a ∀ a ∈ N.
(ii) If * is a commutative binary operation on N, then a * (b * c) = (c * b) * a
Ans.
(i) Define an operation * on N as a * b = a + b ∀ a, b ∈ N
Then, in particular, for b = a = 3, we have
3 * 3 = 3 + 3 = 6 ≠ 3
Therefore, statement (i) is false.
(ii) R.H.S. = (c * b) * a
= (b * c) * a [* is commutative]
= a * (b * c) [Again, as * is commutative]
= L.H.S.
∴ a * (b * c) = (c * b) * a
Therefore, statement (ii) is true.
Q.13. Consider a binary operation * on N defined as a * b = a3 + b3. Choose the correct answer.
(a) Is * both associative and commutative?
(b) Is * commutative but not associative?
(c) Is * associative but not commutative?
(d) Is * neither commutative nor associative?
Ans. (b)
Solution. On N, the operation * is defined as a * b = a3 + b3.
For, a, b, ∈ N, we have
a * b = a3 + b3 = b3 + a3 = b * a [Addition is commutative in N]
Therefore, the operation * is commutative.
It can be observed that
(1 * 2) * 3 = (13 + 23) * 3 = (1 + 8) * 3 = 9 * 3 = 93 + 33 = 729 + 27 = 756
and 1* (2 * 3) = 1 * (23 + 33) = 1* (8 + 27) = 1 * 35 = 13 + 353 = 1 + 42875 = 42876
∴ (1 * 2) * 3 ≠ 1 * (2 * 3), where 1, 2, 3 ∈ N
Therefore, the operation * is not associative.
Hence, the operation * is commutative, but not associative.
FAQs on NCERT Solutions (Exercise 1.4) - Relations and Functions - Class 12
| 1. What are the key concepts covered in NCERT Solutions (Exercise 1.4) - Relations and Functions Class 12? |  |
| 2. How can relations be represented and defined in mathematics? |  |
| 3. What are the different types of relations discussed in NCERT Solutions (Exercise 1.4) - Relations and Functions Class 12? |  |
| 4. What is the composition of relations? |  |
| 5. What is the significance of functions in relations and how are they defined? |  |















