Animal Jumps NCERT Solutions | Mathematics for Class 5 PDF Download
Page No. 165
Q: Do you see why 12 is a multiple of 1, 2, 3, 4, 6, and 12?
Ans:
2 × 6 = 12, 3 × 4 = 12, 12 × 1 = 12
Let Us Do
Q1: Make different arrays for the following numbers. Identify the factors in each case.
(a) 10
Ans:
Factors of 10 are 1, 2, 5, and 10.
(b) 14
Ans:
Factors of 14 are 1, 2, 7, and 14.
Ans:
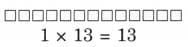
Factors of 13 are 1 and 13 only. So, 13 is a prime number.
(d) 20
Ans:
Factors of 20 are 1, 2, 4, 5, 10, and 20.
(e) 25
Ans: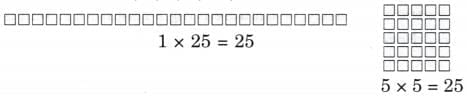
Factors of 25 are 1, 5, and 25.
Ans:

Factors of 32 are 1, 2, 4, 8, 16, and 32.
(g) 37

Factors of 37 are 1 and 37 only. So, 37 is a prime number.
(h) 46
Ans: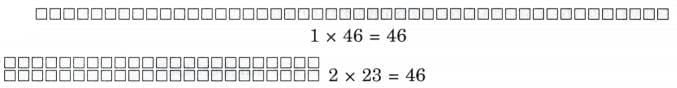
Factors of 46 are 1, 2, 23 and 46.
(i) 54
Ans: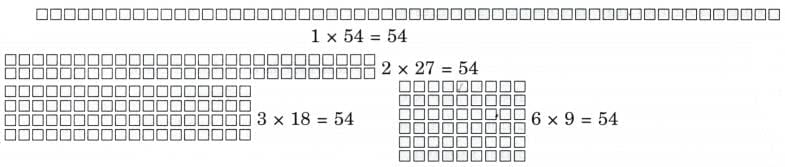
Factors of 54 are 1, 2, 3, 6, 9, 18, 27 and 54.
Q: What do you notice about the common multiples of 3 and 4? Discuss in class.
Ans: Do it yourself.
Page No. 166-170
Let Us Do
(a) 2 and 3
Ans:
2 and 3
Multiples of 2:
2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, …
Multiples of 3:
3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, …
5 common multiples of 2 and 3 are: 6, 12, 18, 24, and 30.
(b) 5 and 8
Ans:
Multiples of 5:
5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105, 110, 115, 120, 125, 130, 135, 140, 145, 150, 155, 160, 165, 170, 175, 180, 185, 190, 195, 200, …
Multiples of 8:
8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120, 128, 136, 144, 152, 160, 168, 176, 184, 192, 200, …
5 common multiples of 5 and 8 are: 40, 80, 120, 160, and 200.
(c) 2 and 4
Ans:
Multiples of 2:
2, 4, 6, 8, 10, 12, 14, 16, 18, 20, …
Multiples of 4:
4, 8, 12, 16, 20, 24, 28, 32, …
5 common multiples of 2 and 4 are:
4, 8, 12, 16, and 20.
(d) 3 and 9
Ans:
Multiples of 3:
3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, …….
Multiples of 9:
9, 18, 27, 36, 45, 54 …
5 common multiples of 3 and 9 are:
9, 18, 27, 36, and 45.
(e) 5 and 10
Ans:
Multiples of 5:
5, 10, 15, 20, 25, 30, 35, 40, 45, 50, …
Multiples of 10:
10, 20, 30, 40, 50, 60, 70, 80, 90, 100, …
5 common multiples of 5 and 10 are:
10, 20, 30, 40, and 50.
(f) 9 and 12
Ans:
Multiples of 9:
9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, 117, 126, 135, 144, 153, 162, 171, 180, 189, …
Multiples of 12:
12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, 144, 156, 168, 180, 192, …
5 common multiples of 9 and 12 are: 36, 72, 108, 144, and 180.
(g) 8 and 12
Ans:
Multiples of 8:
8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120, 128, …
Multiples of 12:
12, 24, 36, 48, 60, 72, 84, 96, 108, 120, ………..
5 common multiples of 8 and 12 are:
24, 48, 72, 96, and 120.
(h) 6 and 8
Ans:
Multiples of 6:
6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96, 102, 108, 114, 120, 126, …
Multiples of 8:
8,16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120, 128, …
5 common multiples of 6 and 8 are: 24, 48, 72, 96 and 120.
(i) 6 and 9
Ans:
Multiples of 6:
6, 12, 18, 24, 30, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96, …
Multiples of 9:
9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, …
5 common multiples of 6 and 9 are: 18, 36, 54, 72 and 90.
Q: What do you notice about the common multiples of different pairs of numbers? Discuss in class.
Ans:
Do it yourself.
Q2: Food is available at the end of a cobbled road. Robby, the rabbit, takes a jump of 4 each time. Deeku, the deer, takes a jump of 6 each time. They both start at 0. Will both Robby and Deeku reach the food? Who will reach first? How do you know? Explain your answer.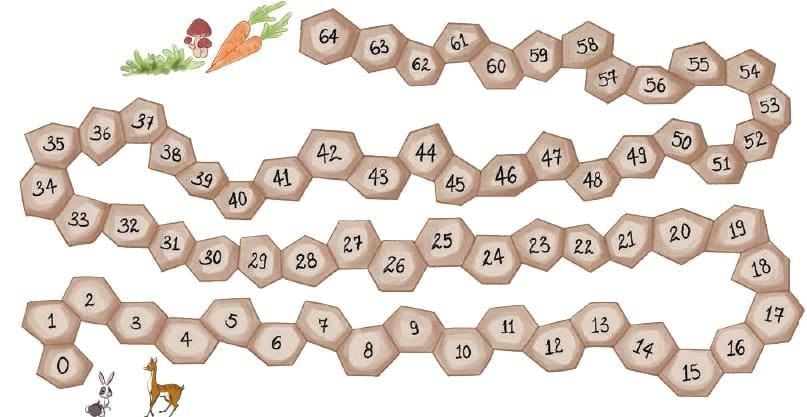 Ans:
Ans:
Robby (Rabbit): Jumps 4 steps at a time. This means Robby will land on multiples of 4 (0, 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64).
Deeku (Deer): Jumps 6 steps at a time. This means Deeku will land on multiples of 6 (0, 6, 12, 18, 24, 30, 36, 42, 48, 54, 60).
Robby: Yes, 64 is a multiple of 4 (4 x 16 = 64). Therefore, Robby will land exactly on 64.
Deeku: No, 64 is not a multiple of 6. (60 is 6 × 10, and 66 is 6 × 11. 64 falls in between). So, Deeku will not land exactly on 64.
Since Robby can land on 64 and Deeku cannot, Robby will be the one to reach the food.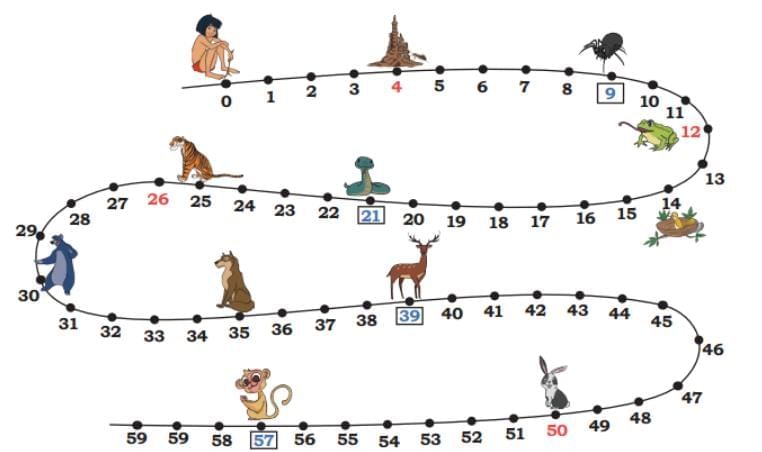
Q: Mowgli’s friends live along the trail on the marked places below. Which of his friends will he be able to visit, if he jumps by 2 steps starting from 0?
Ans: He will meet the ant, the frog, the bird, the bear, and the rabbit.
Q: Did Mowgli meet the ant, frog, bird and the rabbit? Notice their positions— 4, 12, 14, and 50. 2 is a common factor of these numbers.
Ans: Yes, Mowgli met the ant, the frog, the bird, and the rabbit.
Q: Which of his friends will he be able to meet if he jumps by 3 steps?
Ans: If Mowgli jumps by 3 steps, at 9 he met the spider, at 12 he met frog, at 21 he met snake, at 30 he met bear, at 39 he met deer, and at 57 he met with monkey as 3 is a common factor of the numbers 9, 12, 21, 30, 39, and 57.
Ans: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55.
Q: 5 is a common factor of the numbers___________.
Ans: 5 is a common factor of the numbers: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, …
Q: Which numbers will he touch if he jumps by 10 steps?
Ans: 10, 20, 30, 40,50.
Q: 10 is a common factor of the numbers_______.
Ans:10 is a common factor of the numbers: 10, 20, 30, 40, 50, 60, …
Q4: Let us find some common factors of the numbers 24 and 36. Note that all jumps in the following questions start from 0.
(a) Can we jump by 2 steps at a time to reach both 24 and 36? Yes/No. 2 is/is not a common factor of 24 and 36. ,
(b) Can we jump by 3 steps at a time to reach both 24 and 36? Yes/No. 3 is/is not a common factor of 24 and 36.
(c) Can we jump by 4 steps at a time to reach both 24 and 36? Yes/No. 4 is/is not a common factor of 24 and 36.
(d) What other jumps can we take to reach both 24 and 36?
(e) How many common factors can you find for 24 and 36? List them.
(f) What about jumping by 1 step each time to reach both 24 and 36?
Ans:
(a) Yes, we can jump by 2 steps at a time to reach both 24 and 36. 2 is a common factor of 24 and 36.
(b) Yes, we can jump by 3 step at a time to reach both 24 and 36. 3 is a common factor of 24 and 36.
(c) Yes, we can jump by 4 steps at a time to reach both 24 and 36. 4 is a common factor of 24 and 36.
(d) Factors of 24 = 1, 2, 3, 4, 6, 8, 12, 24
Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18, 36
Common factors = 1, 2, 3, 4, 6, 12.
So we can also jump by 6 steps and 12 steps.
(e) The common factors of 24 and 36 are: 1, 2, 3, 4, 6, 12. They are six in number.
(f) Every number is a multiple of 1. So, 24 and 36 are also reached by 1-step jumps.
Q5: What are the common factors of 12 and 13?
Ans: Factors of 12 = 1, 2, 3, 4, 6, 12
Factors of 13 = 1, 13
So, the common factor of 12 and 13 is 1.
Q6: Find which of the following numbers can be reached by jumps of 4 steps?
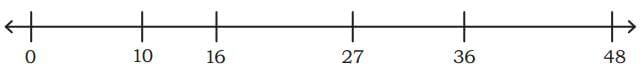 4 is the common factor of the numbers _____________________________.
4 is the common factor of the numbers _____________________________.Ans:
 4 divides 16, 36 and 48 exactly.
4 divides 16, 36 and 48 exactly.So, numbers that can be reached by jumps of 4 steps are 16, 36 and 48.
4 is the common factor of the numbers 16, 36, and 48.
Q7: Find the common factors of the following pairs of numbers.
(a) 12 and 16
Ans:
Factors of 12: (1), (2), 3, (4), 6, and 12.
Factors of 16: (1), (2), (4), 8, and 16.
Common factors of 12 and 16 are: 1, 2 and 4.
(b) 8 and 12
Ans:
Factors of 8: (1), (2), (4), and 8.
Factors of 12: (1), (2), 3, (4), and 12.
Common factors of 8 and 12 are: 1, 2, and 4
(c) 4 and 16
Ans:
Factors of 4: (1), (2), and (4).
Factors of 16: (1), (2), (4), 8, and 16. Common factors of 4 and 16 are: 1, 2 and 4
(d) 2 and 9
Ans:
Factors of 2: (1), and 2 Factors of 9: (1), 3, and 9
Common factor of 2 and 9 is only 1.
(e) 3 and 5
Ans:
Factors of 3: (1) and 3.
Factors of 5: (1) and 5.
Common factor of 3 and 5 is only 1.
(f ) 12 and 15
Ans:
Factors of 12: (1), (2), 3, 4, 6 and 12.
Factors of 15: (1), (3), 5 and 15.
Common factors of 12 and 15 are: 1 and 3.
(g) 20 and 5
Ans:
Factors of 20: (1) 2, 4, (5) 10 and 20.
Factors of 5: (1) and (5).
Common factors of 20 and 5 are: 1 and 5.
(h) 9 and 21
Ans:
Factors of 9: (1), (3) and 9.
Factors of 21: (1), (3), 7 and 21.
Common factors of 9 and 21 are: 1 and 3.
(i) 6 and 27
Ans:
Factors of 6: (1), 2, (3) and 6.
Factors of 27: (1), (3), 9 and 27.
Common factors of 6 and 27 are: 1 and 3.
Q: What do you notice about the common factors of different pairs of numbers? Discuss in class.
Ans: Do it yourself.
Q8: State whether the following statements are true (T) or false (F). .
(a) Factors of even numbers must be even.
Ans: Example: Factors of 12 = 1, 2, 3, 4, 6, 12, which includes the odd numbers 1 and 3.
False.
(b) Multiples of odd numbers cannot be even.
Ans: Example: Multiples of 3 = 3, 6, 9, 12, which includes even numbers 6, 12.
False.
(c) Factors of odd numbers cannot be even.
Ans: Example: Factors of 15 = 1, 3, 5, 15 → all odd.
Example: Factors of 9 = 1, 3, 9 → all odd.
True.
(d) One of the common multiples of two consecutive numbers is their product.
Ans: Example: Consecutive numbers 4 and 5
Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40….
Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60….
Common multiples: 20, 40, 60…
True.
(e) The only common factor of any two consecutive numbers is 1.
Ans: Example: Consecutive numbers 6 and 7
Factors of 6: 1, 2, 3, 6
Factors of 7: 1, 7
Common factors: 1
True.
(f) 0 cannot be a factor of any number.
Ans: True
Q9: Sher Khan, the tiger, goes hunting every 3rd day. Bagheera, the panther, goes hunting every 5th day. If both of them start on the same day, on which days will they be hunting together?
Ans: Sher Khan hunts every 3rd day → 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33 …
Bagheera hunts every 5th day → 5, 10, 15, 20, 25, 30, 35, 40, 45, 50 …
The days on which they will be hunting together are the common multiples of 3 and 5.
Common multiples = 15, 30, 45 …..
So, Sher Khan and Bagheera will hunt together on every 15th day, 30th day, 45th day, and so on.
Q10: (a) In the trail shown earlier, Sher Khan’s house is on number 25 and that of Baloo the bear is on number 30. Mowgli wants to meet his friend Baloo the bear but wants to avoid Sher Khan’s house. How long (in steps) could each jump be?
(b) What number of jumps (in steps) he could choose so that he can meet both Kaa, the snake, at 21 and Akela, the wolf, at 35?
Ans:
(a) To meet Baloo the bear and avoid Sher Khan, Mowgli must choose a jump length that is a factor of 30 but not a factor of 25.
Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30.
Factors of 25: 1, 5, 25.
Common factors: 1, 5.
Removing common factors from the factors of 30, we get 2, 3, 6, 10, 15, and 30.
So, possible jump lengths could be 2, 3, 6, 10, 15, and 30.
(b) To meet Kaa the snake and Akela the wolf, Mowgli must choose a jump length that is a common factor of both 21 and 35.
Factors of 21: 1, 3, 7, 21.
Factors of 35: 1, 5, 7, 35.
Common factors: 1 and 7.
So, possible jump lengths could be 1 and 7.
Q11: Sort the following numbers into those that are
(a) divisible by 2 only
(b) divisible by 5 only
(c) divisible by 10 only
(d) divisible by 2, 5, and 10.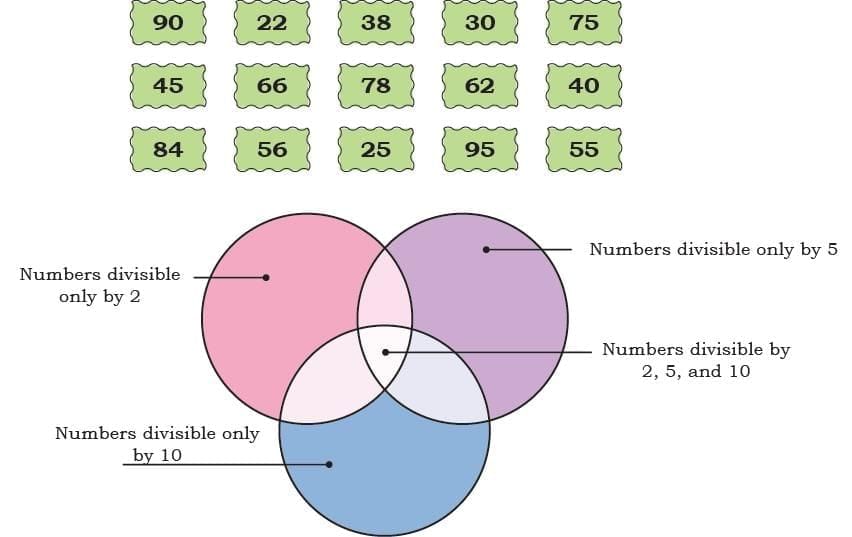 Ans:
Ans:
(a) 22, 30, 38, 40, 56, 62, 66, 78, 84, 90.
(b) 25, 30, 40, 45, 55, 75, 90, 95.
(c) 30, 40, 90.
(d) 30, 40, 90.
|
95 videos|462 docs|47 tests
|
FAQs on Animal Jumps NCERT Solutions - Mathematics for Class 5
| 1. What are some examples of animals that can jump, and how do they differ in their jumping abilities? |  |
| 2. How do the physical structures of jumping animals contribute to their ability to leap? |  |
| 3. What adaptations help animals in their jumping abilities? |  |
| 4. Why is jumping an important survival mechanism for certain animals? |  |
| 5. How do scientists study the jumping abilities of animals, and what have they discovered? |  |





















