NCERT Solutions for Class 7 Maths - Triangle and Its Properties
| Table of contents |

|
| Exercise 6.1 |

|
| Exercise 6.2 |

|
| Exercise 6.3 |

|
| Exercise 6.4 |

|
| Exercise 6.5 |

|
Exercise 6.1
Q1: In ΔPQR, D is the mid-point of ____________
PD is_____________
Is QM = MR?Ans:
We know that,
Altitude: An altitude has one end point at a vertex of the triangle and other on the line containing the opposite side.
Median: A median connects a vertex of a triangle to the mid-point of the opposite side.
- Since PM is perpendicular to QR
Therefore, PM is altitude. - Since, QD = DR
Therefore, PD is median.
No, QM ≠ MR.
Q2: Draw rough sketches for the following:
(a) In ΔABC, BE is a median.
Ans: Here, BE is a median in ΔABC and AE = EC.
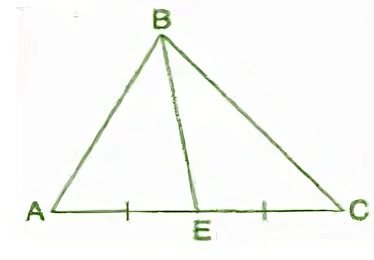
A median connects a vertex of a triangle to the mid-point of the opposite side.
(b) In ΔPQR, PQ and PR are altitudes of the triangle.
Ans: Here, PQ and PR are the altitudes of the ΔPQR and RP ⊥ QP.
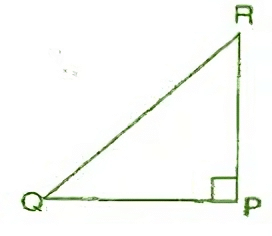
An altitude has one end point at a vertex of the triangle and other on the line containing the opposite side.
(c) In ΔXYZ, YL is an altitude in the exterior of the triangle.
Ans: YL is an altitude in the exterior of ΔXYZ.
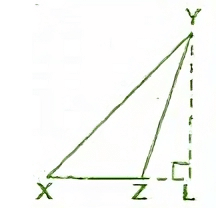
In the figure, we may observe that for ΔXYZ, YL is an altitude drawn exteriorly to side XZ which is extended up to point L.
Q3: Verify by drawing a diagram if the median and altitude of a isosceles triangle can be same.
Ans: 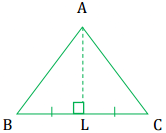
Isosceles triangle means any two sides are same.
Take ΔABC and draw the median when AB = AC.
AL is the median and altitude of the given triangle.
Exercise 6.2
Q1: Find the value of the unknown exterior angle x in the following diagrams:
(i)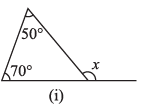
Ans: We Know That,
An exterior angle of a triangle is equal to the sum of its interior opposite angles.
= x = 50° + 70°
= x = 120°
(ii)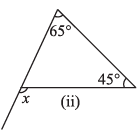
Ans: We Know That,
An exterior angle of a triangle is equal to the sum of its interior opposite angles.
= x = 65° + 45°
= x = 110°
(iii)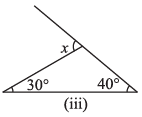
Ans: We Know That,
An exterior angle of a triangle is equal to the sum of its interior opposite angles.
= x = 30° + 40°
= x = 70°
(iv)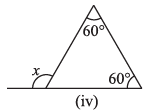
Ans: We Know That,
An exterior angle of a triangle is equal to the sum of its interior opposite angles.
= x = 60° + 60°
= x = 120°
(v)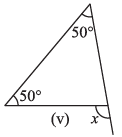
Ans: We Know That,
An exterior angle of a triangle is equal to the sum of its interior opposite angles.
= x = 50° + 50°
= x = 100°
(vi)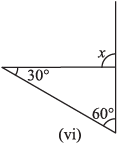
Ans: We Know That,
An exterior angle of a triangle is equal to the sum of its interior opposite angles.
= x = 30° + 60°
= x = 90°
Q2: Find the value of the unknown interior angle x in the following figures:
(i)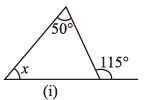
Ans: We Know That,
An exterior angle of a triangle is equal to the sum of its interior opposite angles.
= x + 50° = 115°
By transposing 50° from LHS to RHS it becomes – 50°
= x = 115° – 50°
= x = 65°
(ii)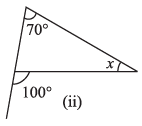
Ans: We Know That,
An exterior angle of a triangle is equal to the sum of its interior opposite angles.
= 70° + x = 100°
By transposing 70° from LHS to RHS it becomes – 70°
= x = 100° – 70°
= x = 30°
(iii)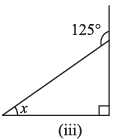
Ans: We Know That,
An exterior angle of a triangle is equal to the sum of its interior opposite angles.
The given triangle is a right angled triangle. So the angle opposite to the x is 90°.
= x + 90° = 125°
By transposing 90° from LHS to RHS it becomes – 90°
= x = 125° – 90°
= x = 35°
(iv)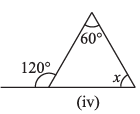
Ans: We Know That,
An exterior angle of a triangle is equal to the sum of its interior opposite angles.
= x + 60° = 120°
By transposing 60° from LHS to RHS it becomes – 60°
= x = 120° – 60°
= x = 60°
(v)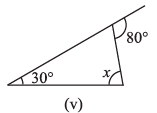
Ans: We Know That,
An exterior angle of a triangle is equal to the sum of its interior opposite angles.
The given triangle is a right angled triangle. So the angle opposite to the x is 90°.
= x + 30° = 80°
By transposing 30° from LHS to RHS it becomes – 30°
= x = 80° – 30°
= x = 50°
(vi)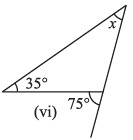
Ans: We Know That,
An exterior angle of a triangle is equal to the sum of its interior opposite angles.
The given triangle is a right angled triangle. So the angle opposite to the x is 90°.
= x + 35° = 75°
By transposing 35° from LHS to RHS it becomes – 35°
= x = 75° – 35°
= x = 40°
Exercise 6.3
Q1: Find the value of unknown x in the following diagrams:
(i)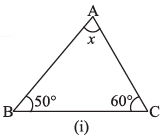
Ans: In ΔABC,
∠ BAC + ∠ ACB + ∠ ABC = 180° [ By angle sum property of a triangle]
⇒ x + 50°+ 60° = 180°
⇒ x + 110° = 180°
⇒ x = 180°-110° = 70°
(ii)
Ans: In ΔPQR,
∠ RPQ + ∠ PQR + ∠ RPQ = 180° [By angle sum property of a triangle]
⇒ 90° + 30°+ x = 180°
⇒ x + 120° = 180°
⇒ x= 180° - 120°= 60°
(iii)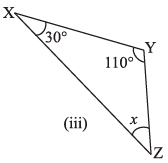
Ans: In ΔXYZ,
∠ ZXY + ∠ XYZ + ∠ YZX = 180° [By angle sum property of a triangle]
⇒ 30° + 110° + x = 180°
⇒ x + 140° = 180°
⇒ x = 180° - 140° = 40°
(iv)
Ans: In the given isosceles triangle,
x + x + 50° = 180° [By angle sum property of a triangle]
⇒ 2x + 50°= 180°
⇒ 2x = 180°- 50°
⇒ 2x = 130°
⇒ x = 130° / 2 = 65°
(v)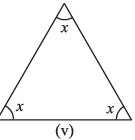
Ans: In the given equilateral triangle,
x + x + x = 180° [By angle sum property of a triangle]
⇒ 3x = 180°
⇒ x = 180° / 3 = 60°
(vi)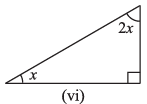
Ans: In the given right angled triangle,
x + 2x + 90° = 180° [By angle sum property of a triangle)
⇒ 3x + 90° = 180°
⇒ 3x = 180°- 90°
⇒ 3x = 90°
⇒ x = 90° / 3 = 30°
Q2: Find the values of the unknowns x and y in the following diagrams:
(i)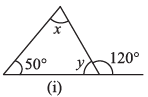
Ans: 50° + x = 120° [Exterior angle property of a Δ]
⇒ x = 120° - 50° = 70°
Now, 50° + x + y = 180° [Angle sum property of a Δ]
⇒ 50° + 70° + y = 180°
⇒ 120° + y = 180°
⇒ y = 180° - 120° = 60°
(ii)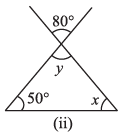
Ans: y = 80° ..... (i) [Vertically opposite angle]
Now, 50° + x + y = 180° [Angle sum property of a Δ]
⇒ 50° + 80°+y = 180° [From equation (i)]
⇒ 130° + y = 180°
⇒ y = 180° - 130° = 50°
(iii)
Ans: 50°+ 60° = x (Exterior angle property of a Δ]
x = 110°
Now 50° + 60°+ y = 180° [Angle sum property of a Δ]
⇒ 110° + y = 180°
⇒ y = 180° - 110°
⇒ y = 70°
(iv)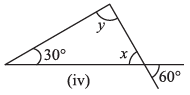
Ans: x = 60° ..... (i) [Vertically opposite angle]
Now, 30° + x + y = 180° [Angle sum property of a Δ ]
⇒ 50° + 60° + y = 180° [From equation (i)]
⇒ 90° + y = 180°
⇒ y = 180° - 90° = 90°
(v)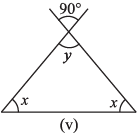
Ans: y = 90° ....(i) [Vertically opposite angle]
Now, y + x + x = 180° [Angle sum property of a Δ]
⇒ 90° + 2x = 180° [From equation (i)]
⇒ 2x = 180°- 90°
⇒ 2x = 90°
⇒ x = 90° / 2 = 45°
(vi)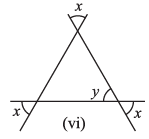
Ans: x = y ...(i) [Vertically opposite angle]
Now, x + x + y = 180° [Angle sum property of a Δ]
⇒ 2x + x = 180° [From equation (i)]
⇒ 3x = 180°
⇒ x = 180° / 3 = 60°
Exercise 6.4
Q1: Is it possible to have a triangle with the following sides?
(i) 2 cm, 3 cm, 5 cm
Ans:
Clearly, we have:
= (2 + 3) = 5
= 5 = 5
Thus, the sum of any two of these numbers is not greater than the third.
Hence, it is not possible to draw a triangle whose sides are 2 cm, 3 cm and 5 cm.
(ii) 3 cm, 6 cm, 7 cm
Ans:
Clearly, we have:
(3 + 6) = 9 > 7
(6 + 7) = 13 > 3
(7 + 3) = 10 > 6
Thus, the sum of any two of these numbers is greater than the third.
Hence, it is possible to draw a triangle whose sides are 3 cm, 6 cm and 7 cm.
(iii) 6 cm, 3 cm, 2 cm
Ans:
Clearly, we have:
(3 + 2) = 5 < 6
Thus, the sum of any two of these numbers is less than the third.
Hence, it is not possible to draw a triangle whose sides are 6 cm, 3 cm and 2 cm.
Q2: Take any point O in the interior of a triangle PQR. Is
(i) OP + OQ > PQ?
(ii) OQ + OR > QR?
(iii) OR + OP > RP?
 Ans:
Ans:
If we take any point O in the interior of a triangle PQR and join OR, OP, OQ.
Then, we get three triangles ΔOPQ, ΔOQR and ΔORP is shown in the figure below.
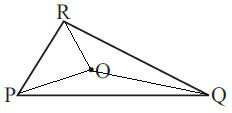 We know that,
We know that,
The sum of the length of any two sides is always greater than the third side.
(i) Yes, ΔOPQ has sides OP, OQ and PQ.
So, OP + OQ > PQ
(ii) Yes, ΔOQR has sides OR, OQ and QR.
So, OQ + OR > QR
(iii) Yes, ΔORP has sides OR, OP and PR.
So, OR + OP > RP
Q3: AM is a median of a triangle ABC.
Is AB + BC + CA > 2 AM?
(Consider the sides of triangles ΔABM and ΔAMC.)
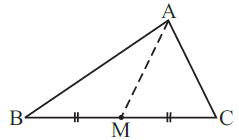 Ans: We know that,
Ans: We know that,
The sum of the length of any two sides is always greater than the third side.
Now consider the ΔABM,
Here, AB + BM > AM … [equation i]
Then, consider the ΔACM
Here, AC + CM > AM … [equation ii]
By adding equation [i] and [ii] we get,
AB + BM + AC + CM > AM + AM
From the figure we have, BC = BM + CM
AB + BC + AC > 2 AM
Hence, the given expression is true.
Q4: ABCD is a quadrilateral.
Is AB + BC + CD + DA > AC + BD?
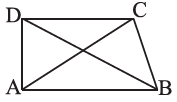
Ans: We know that,
The sum of the length of any two sides is always greater than the third side.
Now consider the ΔABC,
Here, AB + BC > CA … [equation i]
Then, consider the ΔBCD
Here, BC + CD > DB … [equation ii]
Consider the ΔCDA
Here, CD + DA > AC … [equation iii]
Consider the ΔDAB
Here, DA + AB > DB … [equation iv]
By adding equation [i], [ii], [iii] and [iv] we get,
AB + BC + BC + CD + CD + DA + DA + AB > CA + DB + AC + DB
2AB + 2BC + 2CD + 2DA > 2CA + 2DB
Take out 2 on both the side,
2(AB + BC + CA + DA) > 2(CA + DB)
AB + BC + CA + DA > CA + DB
Hence, the given expression is true.
Q5: ABCD is a quadrilateral. Is AB + BC + CD + DA < 2 (AC + BD)?
Ans: Let us consider ABCD is quadrilateral and P is the point where the diagonals intersect. As shown in the figure below,
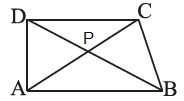
We know that,
The sum of the length of any two sides is always greater than the third side.
Now consider the ΔPAB,
Here, PA + PB > AB … [equation i]
Then, consider the ΔPBC
Here, PB + PC > BC … [equation ii]
Consider the ΔPCD
Here, PC + PD > CD … [equation iii]
Consider the ΔPDA
Here, PD + PA > DA … [equation iv]
By adding equation [i], [ii], [iii] and [iv] we get,
PA + PB + PB + PC + PC + PD + PD + PA > AB + BC + CD + DA
2PA + 2PB + 2PC + 2PD > AB + BC + CD + DA
2PA + 2PC + 2PB + 2PD > AB + BC + CD + DA
2(PA + PC) + 2(PB + PD) > AB + BC + CD + DA
From the figure we have, AC = PA + PC and BD = PB + PD
Then,
2AC + 2BD > AB + BC + CD + DA
2(AC + BD) > AB + BC + CD + DA
Hence, the given expression is true.
Q6: The lengths of two sides of a triangle are 12 cm and 15 cm. Between what two measures should the length of the third side fall?
Ans: We know that,
The sum of the length of any two sides is always greater than the third side.
From the question, it is given that two sides of the triangle are 12 cm and 15 cm.
So, the third side’s length should be less than the sum of other two sides,
12 + 15 = 27 cm.
Then, it is given that the third side cannot not be less than the difference of the two sides, 15 – 12 = 3 cm
So, the length of the third side falls between 3 cm and 27 cm.
Exercise 6.5
Q1: PQR is a triangle, right-angled at P. If PQ = 10 cm and PR = 24 cm, find QR.
Ans:
Let us draw a rough sketch of right-angled triangle
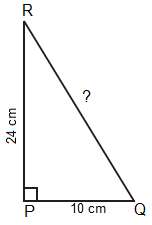 By the rule of Pythagoras Theorem,
By the rule of Pythagoras Theorem,
Pythagoras theorem states that for any right angled triangle, the area of the square on the hypotenuse is equal to the sum of the areas of square on the legs.
In the above figure RQ is the hypotenuse,
QR2 = PQ2 + PR2
QR2 = 102 + 242
QR2 = 100 + 576
QR2 = 676
QR = √676
QR = 26 cm
Hence, the length of the hypotenuse QR = 26 cm.
Q2: ABC is a triangle, right-angled at C. If AB = 25 cm and AC = 7 cm, find BC.
Ans:
Let us draw a rough sketch of right-angled triangle

By the rule of Pythagoras Theorem,
Pythagoras theorem states that for any right angled triangle, the area of the square on the hypotenuse is equal to the sum of the areas of square on the legs.
In the above figure RQ is the hypotenuse,
AB2 = AC2 + BC2
252 = 72 + BC2
625 = 49 + BC2
By transposing 49 from RHS to LHS it becomes – 49
BC2 = 625 – 49
BC2 = 576
BC = √576
BC = 24 cm
Hence, the length of the BC = 24 cm.
Q3: A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.
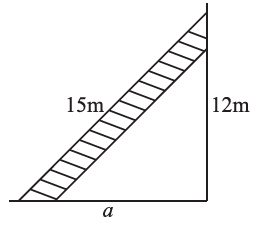 Ans: By the rule of Pythagoras Theorem,
Ans: By the rule of Pythagoras Theorem,
Pythagoras theorem states that for any right angled triangle, the area of the square on the hypotenuse is equal to the sum of the areas of square on the legs.
In the above figure RQ is the hypotenuse,
152 = 122 + a2
225 = 144 + a2
By transposing 144 from RHS to LHS it becomes – 144
a2 = 225 – 144
a2 = 81
a = √81
a = 9 m
Hence, the length of a = 9 m.
Q4: Which of the following can be the sides of a right triangle?
(i) 2.5 cm, 6.5 cm, 6 cm.
(ii) 2 cm, 2 cm, 5 cm.
(iii) 1.5 cm, 2cm, 2.5 cm.
In the case of right-angled triangles, identify the right angles.
Ans:
(i) Let a = 2.5 cm, b = 6.5 cm, c = 6 cm
Let us assume the largest value is the hypotenuse side i.e. b = 6.5 cm.
Then, by Pythagoras theorem,
b2 = a2 + c2
6.52 = 2.52 + 62
42.25 = 6.25 + 36
42.25 = 42.25
The sum of square of two side of triangle is equal to the square of third side,
∴ The given triangle is right-angled triangle.
Right angle lies on the opposite of the greater side 6.5 cm.
(ii) Let a = 2 cm, b = 2 cm, c = 5 cm
Let us assume the largest value is the hypotenuse side i.e. c = 5 cm.
Then, by Pythagoras theorem,
c2 = a2 + b2
52 = 22 + 22
25 = 4 + 4
25 ≠ 8
The sum of square of two side of triangle is not equal to the square of third side,
∴ The given triangle is not right-angled triangle.
(iii) Let a = 1.5 cm, b = 2 cm, c = 2.5 cm
Let us assume the largest value is the hypotenuse side i.e. b = 2.5 cm.
Then, by Pythagoras theorem,
b2 = a2 + c2
2.52 = 1.52 + 22
6.25 = 2.25 + 4
6.25 = 6.25
The sum of square of two side of triangle is equal to the square of third side,
∴ The given triangle is right-angled triangle.
Right angle lies on the opposite of the greater side 2.5 cm.
Q5: A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
Ans:
Let ABC is the triangle and B is the point where tree is broken at the height 5 m from the ground.
Tree top touches the ground at a distance of AC = 12 m from the base of the tree,
 By observing the figure we came to conclude that right angle triangle is formed at A.
By observing the figure we came to conclude that right angle triangle is formed at A.
From the rule of Pythagoras theorem,
BC2 = AB2 + AC2
BC2 = 52 + 122
BC2 = 25 + 144
BC2 = 169
BC = √169
BC = 13 m
Then, the original height of the tree = AB + BC
= 5 + 13
= 18 m
Q6: Angles Q and R of a ΔPQR are 25º and 65º.
Write which of the following is true:
(i) PQ2 + QR2 = RP2
(ii) PQ2 + RP2 = QR2
(iii) RP2 + QR2 = PQ2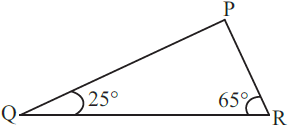 Ans:
Ans:
Given that ∠Q = 25º, ∠R = 65º
Then, ∠P =?
We know that sum of the three interior angles of triangle is equal to 180o.
∠PQR + ∠QRP + ∠RPQ = 180º
25º + 65º + ∠RPQ = 180º
90º + ∠RPQ = 180º
∠RPQ = 180 – 90
∠RPQ = 90º
Also, we know that side opposite to the right angle is the hypotenuse.
∴ QR2 = PQ2 + PR2
Hence, (ii) is true
Q7: Find the perimeter of the rectangle whose length is 40 cm and a diagonal is 41 cm.
Ans:
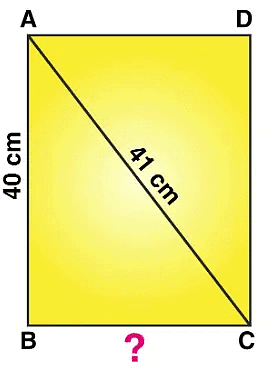
Let ABCD be the rectangular plot.
Then, AB = 40 cm and AC = 41 cm
BC =?
According to Pythagoras theorem,
From right angle triangle ABC, we have:
= AC2 = AB2 + BC2
= 412 = 402 + BC2
= BC2 = 412 – 402
= BC2 = 1681 – 1600
= BC2 = 81
= BC = √81
= BC = 9 cm
Hence, the perimeter of the rectangle plot = 2 (length + breadth)
Where, length = 40 cm, breadth = 9 cm
Then,
= 2(40 + 9)
= 2 × 49
= 98 cm
Q8: The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.
Ans:
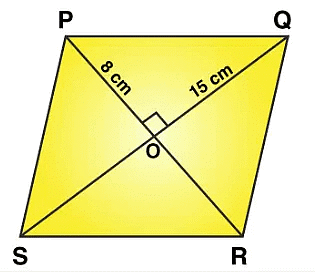
Let PQRS be a rhombus, all sides of rhombus has equal length and its diagonal PR and SQ are intersecting each other at a point O. Diagonals in rhombus bisect each other at 90o.
So, PO = (PR/2)
= 16/2
= 8 cm
And, SO = (SQ/2)
= 30/2
= 15 cm
Then, consider the triangle POS and apply the Pythagoras theorem,
PS2 = PO2 + SO2
PS2 = 82 + 152
PS2 = 64 + 225
PS2 = 289
PS = √289
PS = 17 cm
Hence, the length of side of rhombus is 17 cm
Now,
Perimeter of rhombus = 4 × side of the rhombus
= 4 × 17
= 68 cm
∴ Perimeter of rhombus is 68 cm.
|
77 videos|386 docs|39 tests
|
FAQs on NCERT Solutions for Class 7 Maths - Triangle and Its Properties
| 1. What are the properties of triangles that are important for solving problems? |  |
| 2. How do you determine if a triangle is scalene, isosceles, or equilateral? |  |
| 3. What is the significance of the Pythagorean theorem in triangles? |  |
| 4. How can the area of a triangle be calculated? |  |
| 5. What is the relationship between the angles and sides of a triangle? |  |
















