NCERT Solutions Class 12 Maths Chapter 4 - Determinants
Q1: Write Minors and Cofactors of the elements of following determinants:
Ans: (i) The given determinant is
Minor of element aij is Mij.
Q2:
Ans:
Q3: Using Cofactors of elements of second row, evaluate Δ =.
Ans: The given determinant is .
We have:
We know that ∆ is equal to the sum of the product of the elements of the second row with their corresponding cofactors.
∆ = a21A21 + a22A22 + a23A23 = 2(7) + 0(7) + 1(−7) = 14 − 7 = 7.
Q4: Using Cofactors of elements of third column, evaluate Δ=
Ans: The given determinant is .
We know that Δ is equal to the sum of the product of the elements of the second row
with their corresponding cofactors.
Hence,
Q5: If ∆ =  and Aij is Cofactors of aij , then value of ∆ is given by
and Aij is Cofactors of aij , then value of ∆ is given by
(A) a11 A31+ a12 A32 + a13 A33
(B) a11 A11 + a12 A21 + a13 A31
(C) a21 A11 + a22 A12 + a23 A13
(D) a11 A11+ a21 A21 + a31 A31
Ans: D
Given : Δ = 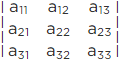
Δ = Sum of products of elements of row (or column) with their corresponding cofactors.
Δ=a11 A11+ a21 A21 + a31 A31
So, option D is correct.
Old NCERT Questions
Q1: For the matrices A and B, verify that (AB)′ = B'A' where
Ans:
Hence,
Q2: Examine the consistency of the system of equations.
x + 2y = 2
2x + 3y = 3
Ans:
The given system of equations is:
x + 2y = 2
2x + 3y = 3
The given system of equations can be written in the form of AX = B, where A is non-singular.
Therefore, A−1 exists.
Hence, the given system of equations is consistent.
Q3: Examine the consistency of the system of equations.
2x − y = 5 x
+ y = 4
Ans: The given system of equations is:
2x − y = 5 x
+ y = 4
The given system of equations can be written in the form of AX = B, where A is non-singular.
Therefore, A−1 exists.
Hence, the given system of equations is consistent.
Q4: Examine the consistency of the system of equations.
x + 3y = 5
2x + 6y = 8
Ans: The given system of equations is:
x + 3y = 5
2x + 6y = 8
The given system of equations can be written in the form of AX = B, where
Thus, the solution of the given system of equations does not exist. Hence, the system of equations is inconsistent.
Q5: Examine the consistency of the system of equations.
x + y + z = 1
2x + 3y + 2z = 2
ax + ay + 2az = 4
Ans: The given system of equations is:
x + y + z = 1 2x
+ 3y + 2z = 2 ax
+ ay + 2az = 4
This system of equations can be written in the form AX = B, where A is non-singular.
Therefore, A−1 exists.
Hence, the given system of equations is consistent.
Q6: Examine the consistency of the system of equations.
3x − y − 2z = 2
2y − z = −1
3x − 5y = 3
Ans: The given system of equations is:
3x − y − 2z = 2
2y − z = −1
3x − 5y = 3
This system of equations can be written in the form of AX = B, where
A is a singular matrix.
Thus, the solution of the given system of equations does not exist. Hence, the system of equations is inconsistent.
Q7: Examine the consistency of the system of equations.
5x − y + 4z = 5
2x + 3y + 5z = 2
5x − 2y + 6z = −1
Ans: The given system of equations is:
5x − y + 4z = 5
2x + 3y + 5z = 2
5x − 2y + 6z = −1
This system of equations can be written in the form of AX = B, where
Therefore, A−1 exists.
Hence, the given system of equations is consistent.
Q8: Solve system of linear equations, using matrix method.
Ans: The given system of equations can be written in the form of AX = B, where
Thus, A is non-singular. Therefore, its inverse exists.
Q9: Solve system of linear equations, using matrix method.
Ans:The given system of equations can be written in the form of AX = B, where
Thus, A is non-singular. Therefore, its inverse exists.
Q10: Solve system of linear equations, using matrix method.
Ans: The given system of equations can be written in the form of AX = B, where
Thus, A is non-singular. Therefore, its inverse exists.
Q11: Solve system of linear equations, using matrix method.
5x + 2y = 3
3x + 2y = 5
Ans: The given system of equations can be written in the form of AX = B, where
Thus, A is non-singular. Therefore, its inverse exists.
Q12: Solve system of linear equations, using matrix method.
Ans: The given system of equations can be written in the form of AX = B, where
Thus, A is non-singular. Therefore, its inverse exists.
Q13: Solve system of linear equations, using matrix method.
x − y + z = 4
2x + y − 3z = 0
x + y + z = 2
Ans: The given system of equations can be written in the form of AX = B, where
Thus, A is non-singular. Therefore, its inverse exists.
Q14: Solve system of linear equations, using matrix method.
2x + 3y + 3z = 5
x − 2y + z = −4
3x − y − 2z = 3
Ans: The given system of equations can be written in the form AX = B, where
Thus, A is non-singular. Therefore, its inverse exists.
Q15: Solve system of linear equations, using matrix method.
x − y + 2z = 7
3x + 4y − 5z = −5
2x − y + 3z = 12
Ans: The given system of equations can be written in the form of AX = B, where
Thus, A is non-singular. Therefore, its inverse exists.
Q16: If find A−1. Using A−1 solve the system of equations
Ans:
Now, the given system of equations can be written in the form of AX = B, where
Q17: The cost of 4 kg onion, 3 kg wheat and 2 kg rice is Rs 60. The cost of 2 kg onion, 4 kg wheat and 6 kg rice is Rs 90. The cost of 6 kg onion 2 kg wheat and 3 kg rice is Rs 70. Find cost of each item per kg by matrix method.
Ans: Let the cost of onions, wheat, and rice per kg be Rs x, Rs y,and Rs z respectively.
Then, the given situation can be represented by a system of equations as:
This system of equations can be written in the form of AX = B, where
Now,
X = A−1 B
Hence, the cost of onions is Rs 5 per kg, the cost of wheat is Rs 8 per kg, and the cost of rice is Rs 8 per kg.
|
203 videos|307 docs|139 tests
|
FAQs on NCERT Solutions Class 12 Maths Chapter 4 - Determinants
| 1. What is a determinant in mathematics? |  |
| 2. How is the determinant of a 2x2 matrix calculated? |  |
| 3. What is the significance of the determinant of a matrix? |  |
| 4. Can determinants be negative? |  |
| 5. How are determinants used in solving systems of linear equations? |  |






















