NCERT Solutions Class 12 Maths Chapter 5 - Continuity & Differentiability
| Table of contents |

|
| Exercise 5.1 |

|
| Exercise 5.2 |

|
| Exercise 5.3 |

|
| Exercise 5.4 |

|
| Exercise 5.5 |

|
| Exercise 5.6 |

|
| Exercise 5.7 |

|
Exercise 5.1
Q1: Prove that the function
Ans:
Therefore, f is continuous at x = 5
Q2: Examine the continuity of the function .
Ans:
Thus, f is continuous at x = 3
Q3: Examine the following functions for continuity.
(a)
(b)
(c)
(d)
Ans:
(c) The given function is
For any real number c ≠ −5, we obtain
Therefore, f is continuous at all real numbers greater than 5.
Hence, f is continuous at every real number and therefore, it is a continuous function.
Q4: Prove that the function is continuous at x = n, where n is a positive integer.
Ans: The given function is f (x) = xn
It is evident that f is defined at all positive integers, n, and its value at n is nn.
Therefore, f is continuous at n, where n is a positive integer.
Q5: Is the function f defined by continuous at x = 0? At x = 1? At x = 2?
Ans: The given function f is
At x = 0,
It is evident that f is defined at 0 and its value at 0 is 0.
The right hand limit of f at x = 1 is,
Therefore, f is continuous at x = 2
Q6: Find all points of discontinuity of f, where f is defined by
Ans: The given function f is
It is evident that the given function f is defined at all the points of the real line.
Let c be a point on the real line. Then, three cases arise.
(i) c < 2
(ii) c > 2
(iii) c = 2
Case (i) c < 2
Therefore, f is continuous at all points x, such that x < 2
Case (ii) c > 2
It is observed that the left and right hand limit of f at x = 2 do not coincide.
Therefore, f is not continuous at x = 2
Hence, x = 2 is the only point of discontinuity of f.
Q7: Find all points of discontinuity of f, where f is defined by
Ans: The given function f is
The given function f is defined at all the points of the real line.
Let c be a point on the real line.
Case I:
Therefore, f is continuous at all points x, such that x < −3
Case II:
It is observed that the left and right hand limit of f at x = 3 do not coincide.
Therefore, f is not continuous at x = 3
Case V:
Therefore, f is continuous at all points x, such that x > 3
Hence, x = 3 is the only point of discontinuity of f.
Q8: Find all points of discontinuity of f, where f is defined by
Ans: The given function f is
It is observed that the left and right hand limit of f at x = 0 do not coincide.
Therefore, f is not continuous at x = 0
Case III:
Therefore, f is continuous at all points x, such that x > 0
Hence, x = 0 is the only point of discontinuity of f.
Q9: Find all points of discontinuity of f, where f is defined by
Ans: The given function f is
Therefore, the given function is a continuous function.
Hence, the given function has no point of discontinuity.
Q10: Find all points of discontinuity of f, where f is defined by
Ans:
The given function f is
The given function f is defined at all the points of the real line.
Let c be a point on the real line.
Case I:
Therefore, f is continuous at all points x, such that x > 1
Hence, the given function f has no point of discontinuity.
Q11: Find all points of discontinuity of f, where f is defined by
Ans: The given function f is
The given function f is defined at all the points of the real line.
Let c be a point on the real line.
Case I:
Therefore, f is continuous at all points x, such that x > 2
Thus, the given function f is continuous at every point on the real line.
Hence, f has no point of discontinuity.
Question 12: Find all points of discontinuity of f, where f is defined by
Ans: The given function f is
The given function f is defined at all the points of the real line.
Let c be a point on the real line.
Case I:
Therefore, f is continuous at all points x, such that x > 1
Thus, from the above observation, it can be concluded that x = 1 is the only point of discontinuity of f.
Q13: Is the function defined bya continuous function?
Ans: The given function is
The given function f is defined at all the points of the real line.
Let c be a point on the real line.
Case I:
Therefore, f is continuous at all points x, such that x > 1
Thus, from the above observation, it can be concluded that x = 1 is the only point of
discontinuity of f.
Q14: Discuss the continuity of the function f, where f is defined by
Ans: The given function is
The given function is defined at all points of the interval [0, 10].
Let c be a point in the interval [0, 10].
Case I:
Therefore, f is continuous at all points of the interval (1, 3).
Case IV:
Therefore, f is continuous at all points of the interval (3, 10].
Hence, f is not continuous at x = 1 and x = 3
Q15: Discuss the continuity of the function f, where f is defined by
Ans: The given function is
The given function is defined at all points of the real line.
Let c be a point on the real line.
Case I:
Therefore, f is continuous at all points of the interval (0, 1).
Case IV:
Therefore, f is continuous at all points x, such that x > 1
Hence, f is not continuous only at x = 1
Q16: Discuss the continuity of the function f, where f is defined by
Ans: The given function f is
The given function is defined at all points of the real line.
Let c be a point on the real line.
Case I:
Therefore, f is continuous at x = −1
Case III:
Therefore, f is continuous at all points x, such that x > 1
Thus, from the above observations, it can be concluded that f is continuous at all points of the real line.
Q17: Find the relationship between a and b so that the function f defined by is continuous at x = 3.
Ans: The given function f is
If f is continuous at x = 3, then
Q18: For what value of is the function defined by continuous at x = 0? What about continuity at x = 1?
Ans: The given function f is
If f is continuous at x = 0, then
Therefore, there is no value of λ for which f is continuous at x = 0 At x = 1,
f (1) = 4x + 1 = 4 × 1 + 1 = 5
Therefore, for any values of λ, f is continuous at x = 1
Q19: Show that the function defined by g(x)= x-[x] is discontinuous at all integral point. Here [x] denotes the greatest integer less than or equal to x.
Ans: The given function is g(x)= x-[x]
It is evident that g is defined at all integral points.
Let n be an integer.
Then,
It is observed that the left and right hand limits of f at x = n do not coincide.
Therefore, f is not continuous at x = n
Hence, g is discontinuous at all integral points.
Q20: Is the function defined by continuous at x = p?
Ans: The given function is
It is evident that f is defined at x = p
Therefore, the given function f is continuous at x = π
Q21: Discuss the continuity of the following functions.
(a) f (x) = sin x + cos x
(b) f (x) = sin x − cos x
(c) f (x) = sin x × cos x
Ans: It is known that if g and h are two continuous functions, then
g+h, g-h, and g.h are also continuous.
It has to proved first that g (x) = sin x and h (x) = cos x are continuous functions.
Let g (x) = sin x
It is evident that g (x) = sin x is defined for every real number.
Let c be a real number. Put x = c + h
If x → c, then h → 0
Therefore, g is a continuous function.
Let h (x) = cos x
It is evident that h (x) = cos x is defined for every real number.
Let c be a real number. Put x = c + h
If x → c, then h → 0
h (c) = cos c
Therefore, h is a continuous function.
Therefore, it can be concluded that
(a) f (x) = g (x) + h (x) = sin x + cos x is a continuous function
(b) f (x) = g (x) − h (x) = sin x − cos x is a continuous function
(c) f (x) = g (x) × h (x) = sin x × cos x is a continuous function.
Q22: Discuss the continuity of the cosine, cosecant, secant and cotangent functions,
Ans: It is known that if g and h are two continuous functions, then
It has to be proved first that g (x) = sin x and h (x) = cos x are continuous functions. Let g (x) = sin x
It is evident that g (x) = sin x is defined for every real number.
Let c be a real number. Put x = c + h
Therefore, g is a continuous function.
Let h (x) = cos x
It is evident that h (x) = cos x is defined for every real number.
Let c be a real number.
Put x = c + h
If x → c, then h → 0
Therefore, h (x) = cos x is continuous function.
Therefore, cotangent is continuous except at x = np, n Î Z
Q23: Find the points of discontinuity of f, where
Ans:
Therefore, f is continuous at x = 0
From the above observations, it can be concluded that f is continuous at all points of
the real line.
Thus, f has no point of discontinuity.
Q24:Determine if f defined byis a continuous function?
Ans: The given function f is
It is evident that f is defined at all points of the real line.
Let c be a real number.
Case I:
Therefore, f is continuous at x = 0
From the above observations, it can be concluded that f is continuous at every point of the real line.
Thus, f is a continuous function.
Q25: Examine the continuity of f, where f is defined by
Ans: The given function f is
It is evident that f is defined at all points of the real line.
Let c be a real number.
Case I:
Therefore, f is continuous at x = 0
From the above observations, it can be concluded that f is continuous at every point of
the real line.
Thus, f is a continuous function.
Q26: Find the values of k so that the function f is continuous at the indicated point.
Ans:
Therefore, the required value of k is 6.
Question 27: Find the values of k so that the function f is continuous at the indicated point.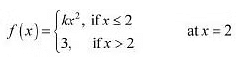
Ans: The given function is
The given function f is continuous at x = 2, if f is defined at x = 2 and if the value of f at x = 2 equals the limit of f at x = 2
It is evident that f is defined at x = 2 and f(2) = k(2)2 = 4k
Q28: Find the values of k so that the function f is continuous at the indicated point.
Ans: The given function is
The given function f is continuous at x = p, if f is defined at x = p and if the value of f at
x = p equals the limit of f at x = p
Q29: Find the values of k so that the function f is continuous at the indicated point.
Ans: The given function f is
The given function f is continuous at x = 5, if f is defined at x = 5 and if the value of f at
x = 5 equals the limit of f at x = 5
Q30: Find the values of a and b such that the function defined by, is a continuous function.
Ans: The given function f is
It is evident that the given function f is defined at all points of the real line.
If f is a continuous function, then f is continuous at all real numbers.
In particular, f is continuous at x = 2 and x = 10
Since f is continuous at x = 2, we obtain
Therefore, the values of a and b for which f is a continuous function are 2 and 1 respectively.
Q31: Show that the function defined by f(x) = cos (x2) is a continuous function.
Ans: The given function is f (x) = cos (x2)
This function f is defined for every real number and f can be written as the composition
of two functions as,
f = g o h, where g (x) = cos x and h (x) = x2
Therefore, g (x) = cos x is continuous function.
h (x) = x2
Clearly, h is defined for every real number.
Let k be a real number, then h (k) = k2
Therefore, h is a continuous function.
It is known that for real-valued functions g and h, such that (g o h) is defined at c, if g is continuous at c and if f is continuous at g (c), then (f o g) is continuous at c.
Therefore, is a continuous function.
Q32: Show that the function defined by is a continuous function.
Ans: The given function is
This function f is defined for every real number and f can be written as the composition of two functions as,
Clearly, g is defined for all real numbers.
Let c be a real number.
Case I:
Therefore, g is continuous at all points x, such that x > 0.
Q33: Examine that sin|x| is a continuous function.
Ans:
This function f is defined for every real number and f can be written as the composition
of two functions as,
Clearly, g is defined for all real numbers.
Let c be a real number.
Case I:
Therefore, g is continuous at x = 0
From the above three observations, it can be concluded that g is continuous at all
points. h (x) = sin x
It is evident that h (x) = sin x is defined for every real number.
Let c be a real number. Put x = c +k
If x → c, then k → 0 h (c) = sin c
Therefore, h is a continuous function.
It is known that for real-valued functions g and h, such that (g o h) is defined at c, if g is continuous at c and if f is continuous at g (c), then (f o g) is continuous at c. is a continuous function.
Q34: Find all the points of discontinuity of f defined by .
Ans: The given function is
The two functions, g and h, are defined as
Clearly, g is defined for all real numbers.
Let c be a real number.
Case I:
From the above three observations, it can be concluded that g is continuous at all
Case II:
Clearly, h is defined for every real number.
Let c be a real number.
Case I:
Therefore, h is continuous at all points x, such that x < −1
Case III:
Therefore, h is continuous at x = −1
From the above three observations, it can be concluded that h is continuous at all points of the real line. g and h are continuous functions. Therefore, f = g − h is also continuous function.
Therefore, f has no point of discontinuity.
Exercise 5.2
Continuity & Differentiability
Question 1: Differentiate the functions with respect to x.
Answer
Question 2: Differentiate the functions with respect to x. cos(sinx)
Answer
Thus, f is a composite function of two functions.
Put t = u (x) = sin x
By chain rule,
Alternate method
Question 3: Differentiate the functions with respect to x.
sin(ax + b)
Answer
Alternate method
Question 4: Differentiate the functions with respect to x.
Answer
Hence, by chain rule, we obtain
Question 5: Differentiate the functions with respect to x.
Answer
The given function is
Put y = p (x) = cx + d
Question 6: Differentiate the functions with respect to x.
Answer
Question 7: Differentiate the functions with respect to x.
Answer
Question 8: Differentiate the functions with respect to x.
Answer
Clearly, f is a composite function of two functions, u and v, such that
Alternate method
Question 9:
Prove that the function f given by is not differentiable at x = 1.
Answer
The given function is
It is known that a function f is differentiable at a point x = c in its domain if both
are finite and equal.
To check the differentiability of the given function at x = 1,
consider the left hand limit of f at x = 1
Since the left and right hand limits of f at x = 1 are not equal, f is not differentiable at x = 1
Question 10:
Prove that the greatest integer function defined by is not differentiable at x = 1 and x = 2.
Answer
The given function f is
It is known that a function f is differentiable at a point x = c in its domain if both
are finite and equal.
To check the differentiability of the given function at x = 1, consider the left hand limit of f at x = 1
Since the left and right hand limits of f at x = 1 are not equal, f is not differentiable at x = 1
To check the differentiability of the given function at x = 2, consider the left hand limit of f at x = 2
Since the left and right hand limits of f at x = 2 are not equal, f is not differentiable at x = 2
Exercise 5.3
Continuity & Differentiability
Question 1:
Answer
Question 2:
Answer
Question 3:
Answer
Question 4:
Answer
The given relationship is
Differentiating this relationship with respect to x, we obtain
Question 5:
Find
Answer
The given relationship is x2 +xy +y2 = 100
Differentiating this relationship with respect to x, we obtain
[Derivative of constant function is 0]
Question 6:
Answer
Question 7:
Answer
Using chain rule, we obtain
Question 8:
Find 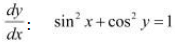
Answer
The given relationship is
Differentiating this relationship with respect to x, we obtain
Question 9:
Find
Answer
Therefore, by quotient rule, we obtain
Question 10:
Answer
Question 11:
Answer
The given relationship is,
On comparing L.H.S. and R.H.S. of the above relationship, we obtain tany/2 = x
Differentiating this relationship with respect to x, we obtain
Question 12:
Answer
The given relationship is
From (1), (2), and (3), we obtain
Differentiating this relationship with respect to x, we obtain
Question 13:
Answer
Question 14:
Find
Answer
Differentiating this relationship with respect to x, we obtain
Question 15:
Find dy/dx
Answer
Differentiating this relationship with respect to x, we obtain
Exercise 5.4
Q1: Differentiate the following w.r.t. x:
Ans: Let y =
By using the quotient rule, we obtain
Q2: Differentiate the following w.r.t. x: esin-1x
Ans: Let y = esin-1x
By using the chain rule, we obtain
Q3: Differentiate the following w.r.t. x:
Ans: Let y =
By using the chain rule, we obtain
Q4: Differentiate the following w.r.t. x: sin(tan-1e-x)
Ans: Let y = sin(tan-1e-x)
By using the chain rule, we obtain
Q5: Differentiate the following w.r.t. x: log(cosex)
Ans: Let y = log(cosex)
By using the chain rule, we obtain
Q6: Differentiate the following w.r.t. x:
Ans:
Q7: Differentiate the following w.r.t. x:
Ans: Let
Q8: Differentiate the following w.r.t. x:
Ans: Let y =
By using the chain rule, we obtain
Q9: Differentiate the following w.r.t. x:
Ans: Let y =
By using the quotient rule, we obtain
Q10: Differentiate the following w.r.t. x: 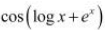 , x>0
, x>0
Ans: Let y = 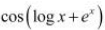
By using the chain rule, we obtain
Exercise 5.5
Continuity & Differentiability
Question 1: Differentiate the function with respect to x.
Answer
Question 2: Differentiate the function with respect to x.
Answer
Let y =
Taking logarithm on both the sides, we obtain
Differentiating both sides with respect to x, we obtain
Question 3: Differentiate the function with respect to x.
Answer
Let y =
Taking logarithm on both the sides, we obtain
Differentiating both sides with respect to x, we obtain
Question 4: Differentiate the function with respect to x. xx - 2sinx
Answer
Let y =
u = xx
Taking logarithm on both the sides, we obtain
Differentiating both sides with respect to x, we obtain
Question 5: Differentiate the function with respect to x.
Answer
Let y =
Taking logarithm on both the sides, we obtain
Differentiating both sides with respect to x, we obtain
Question 6: Differentiate the function with respect to x.
Answer
Differentiating both sides with respect to x, we obtain
Differentiating both sides with respect to x, we obtain
Therefore, from (1), (2), and (3), we obtain
Question 7: Differentiate the function with respect to x.
Answer
Let y =
Differentiating both sides with respect to x, we obtain
Differentiating both sides with respect to x, we obtain
Question 8: Differentiate the function with respect to x.
Answer
Let y =
Differentiating both sides with respect to x, we obtain
Therefore, from (1), (2), and (3), we obtain
Question 9: Differentiate the function with respect to x.
Answer
Let y =
Differentiating both sides with respect to x, we obtain
Question 10: Differentiate the function with respect to x.
Answer
Let y =
Differentiating both sides with respect to x, we obtain
Differentiating both sides with respect to x, we obtain
Question 11: Differentiate the function with respect to x.
Answer
Differentiating both sides with respect to x, we obtain
Differentiating both sides with respect to x, we obtain
Question 12:
Find of function
.
Answer
Differentiating both sides with respect to x, we obtain
Question 13:
Find
Answer
Differentiating both sides with respect to x, we obtain
Question 14:
Find of function
.
Answer
Differentiating both sides, we obtain
Question 15:
Find of function
.
Answer
Differentiating both sides with respect to x, we obtain
Question 16:
Find the derivative of the function given by and
hence find .
Answer
The given relationship is
Taking logarithm on both the sides, we obtain
Differentiating both sides with respect to x, we obtain
Question 17:
Differentiate in three ways mentioned below
(i) By using product rule.
(ii) By expanding the product to obtain a single polynomial.
(iii By logarithmic differentiation.
Do they all give the same answer?
Answer
Let y =
(i)
(ii)
( iii)
Taking logarithm on both the sides, we obtain
Differentiating both sides with respect to x, we obtain
From the above three observations, it can be concluded that all the results of are same.
Question 18: If u, v and w are functions of x, then show that
in two ways-first by repeated application of product rule, second by logarithmic
differentiation.
Answer
Let
By applying product rule, we obtain
Exercise 5.6
Continuity & Differentiability
Question 1:
If x and y are connected parametrically by the equation, without eliminating the
Answer
Question 2: If x and y are connected parametrically by the equation, without eliminating the
parameter, find .
x = a cos θ, y = b cos θ
Answer
The given equations are x = a cos θ and y = b cos θ
Question 3: If x and y are connected parametrically by the equation, without eliminating the
parameter, find .
x = sin t, y = cos 2t
Answer
The given equations are x = sin t and y = cos 2t
Question 4:
If x and y are connected parametrically by the equation, without eliminating the
.
Answer
Question 5: If x and y are connected parametrically by the equation, without eliminating the
Answer
The given equations are
Question 6: If x and y are connected parametrically by the equation, without eliminating the
Answer
The given equations are
Question 7: If x and y are connected parametrically by the equation, without eliminating the
parameter, find .
Answer
The given equations are
Question 8: If x and y are connected parametrically by the equation, without eliminating the
parameter, find
Answer
The given equations are
Question 9: If x and y are connected parametrically by the equation, without eliminating the
parameter, find .
Answer
Question 10: If x and y are connected parametrically by the equation, without eliminating the
parameter, find .
Answer
Question 11:
If
Answer
Hence, proved.
Exercise 5.7
Continuity & Differentiability
Question 1: Find the second order derivatives of the function.
Answer
Let y =
Then,
Question 2: Find the second order derivatives of the function. x20
Answer
Let y = x20
Then,
Question 3: Find the second order derivatives of the function. x.cos x
Answer
Let y = x.cos x
Then,
Question 4: Find the second order derivatives of the function. log x
Answer
Let y = log x
Then,
Question 5: Find the second order derivatives of the function. x3 log x
Answer
Let y = x3 log x
Then,
Question 6: Find the second order derivatives of the function.
Answer
Let y =
Question 7: Find the second order derivatives of the function.
Answer
Let y =
Then,
Question 8: Find the second order derivatives of the function.
Answer
Let y =
Then,
Question 9: Find the second order derivatives of the function.
Answer
Let y =
Then,
Question 10: Find the second order derivatives of the function.
Answer
Let y =
Then,
Question 11: If
Answer
It is given that,
Then,
Hence, proved.
Question 12:
If in terms of y alone.
Answer
It is given that,
Then,
Question 13:
If
Answer
It is given that,
Then,
Hence, proved.
Question 14:
If  , show that
, show that 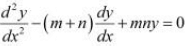
Answer
It is given that, 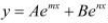
Then,
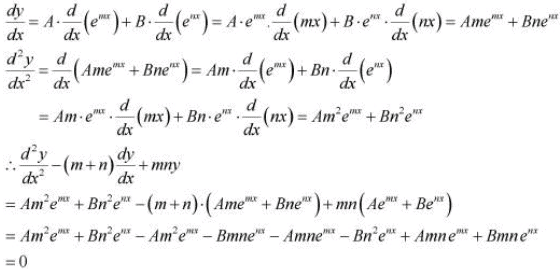
Hence, proved.
Question 15:
If 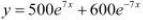 , show that
, show that 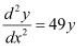
Answer
It is given that, 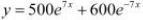
Then,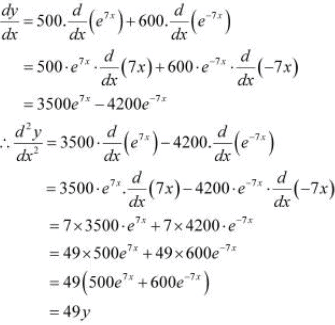
Hence, proved.
Question 16:
If 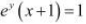 , show that
, show that 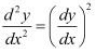
Answer
The given relationship is 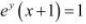
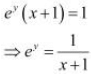
Taking logarithm on both the sides, we obtain

Differentiating this relationship with respect to x, we obtain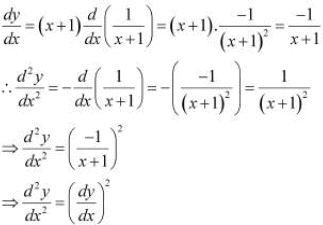
Hence, proved.
Question 17:
If  , show that
, show that 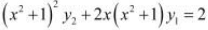
Answer
The given relationship is 
Then,
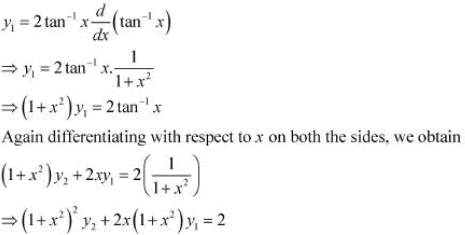
Hence, proved.
|
177 videos|618 docs|160 tests
|
FAQs on NCERT Solutions Class 12 Maths Chapter 5 - Continuity & Differentiability
| 1. What is the definition of continuity in calculus? |  |
| 2. How can we determine if a function is continuous at a specific point? |  |
| 3. What is the importance of continuity and differentiability in calculus? |  |
| 4. How does the concept of continuity relate to the concept of differentiability? |  |
| 5. Can a function be differentiable without being continuous? |  |
















