Continuity & Differentiability
Question 1:
Answer
Question 2:
Answer
Question 3:
Answer
Question 4:
Answer
The given relationship is 
Differentiating this relationship with respect to x, we obtain
Question 5:
Find 
Answer
The given relationship is x2 +xy +y2 = 100
Differentiating this relationship with respect to x, we obtain
[Derivative of constant function is 0]
Question 6:
Answer
Question 7:
Answer
Using chain rule, we obtain
Question 8:
Find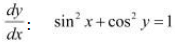 
Answer
The given relationship is
Differentiating this relationship with respect to x, we obtain
Question 9:
Find 
Answer
Therefore, by quotient rule, we obtain
Question 10:
Answer
Question 11:
Answer
The given relationship is,
On comparing L.H.S. and R.H.S. of the above relationship, we obtain tany/2 = x
Differentiating this relationship with respect to x, we obtain
Question 12:
Answer
The given relationship is 
From (1), (2), and (3), we obtain
Differentiating this relationship with respect to x, we obtain
Question 13:
Answer
Question 14:
Find 
Answer
Differentiating this relationship with respect to x, we obtain
Question 15:
Find dy/dx 
Answer
Differentiating this relationship with respect to x, we obtain
FAQs on NCERT Solutions Class 12 Maths Chapter 5 - Continuity & Differentiability
| 1. What is continuity and differentiability in calculus? |  |
Ans. Continuity and differentiability are important concepts in calculus. Continuity refers to the smoothness of a function, where there are no abrupt changes or breaks in its graph. A function is said to be continuous at a point if the limit of the function exists at that point and is equal to the value of the function at that point.
Differentiability, on the other hand, deals with the concept of the derivative of a function. A function is said to be differentiable at a point if the derivative exists at that point. The derivative represents the rate of change of the function at a particular point and provides information about the slope of the tangent line to the graph of the function at that point.
| 2. What are the conditions for a function to be continuous at a point? | |
Ans. For a function to be continuous at a point, three conditions must be satisfied:
1. The function must be defined at that point.
2. The limit of the function as x approaches that point must exist.
3. The value of the function at that point must be equal to the limit.
If any of these conditions are not met, the function is said to be discontinuous at that point.
| 3. How do you determine if a function is differentiable at a point? | |
Ans. To determine if a function is differentiable at a point, we need to check if the derivative exists at that point. The derivative of a function represents the rate of change of the function at a particular point.
To find the derivative at a point, we can use the definition of the derivative or apply differentiation rules, such as the power rule or chain rule, depending on the complexity of the function. If the derivative exists at the given point, then the function is differentiable at that point.
| 4. Can a function be differentiable but not continuous? | |
Ans. No, a function cannot be differentiable at a point if it is not continuous at that point. Differentiability requires the function to be continuous at the point of interest.
If a function has a discontinuity, such as a jump or an essential discontinuity, it cannot have a derivative at that point. The existence of a derivative depends on the smoothness and continuity of the function.
| 5. How are continuity and differentiability related? | |
Ans. Continuity and differentiability are closely related concepts in calculus. A function must be continuous at a point for it to be differentiable at that point.
If a function is continuous at a point, it means that there are no abrupt changes or breaks in its graph at that point. This smoothness allows us to define a derivative, which represents the rate of change of the function at that point.
In simpler terms, differentiability implies continuity, but continuity does not necessarily imply differentiability. A function can be continuous at a point without being differentiable, but it cannot be differentiable at a point without being continuous.
Related Exams
About this Document
|
2.9K Views |
|
4.70/5 Rating |
|
Nov 27, 2024 Last updated |
Document Description: NCERT Solutions Exercise 5.3: Continuity & Differentiability for JEE 2024 is part of JEE preparation. The notes and questions for NCERT Solutions Exercise 5.3: Continuity & Differentiability have been prepared according to the JEE exam syllabus. Information about NCERT Solutions Exercise 5.3: Continuity & Differentiability covers topics like and NCERT Solutions Exercise 5.3: Continuity & Differentiability Example, for JEE 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for NCERT Solutions Exercise 5.3: Continuity & Differentiability.
Introduction of NCERT Solutions Exercise 5.3: Continuity & Differentiability in English is available as part of
our JEE preparation & NCERT Solutions Exercise 5.3: Continuity & Differentiability in Hindi for JEE
courses. Download more important topics, notes, lectures and mock test series for JEE
Exam by signing up for free. JEE: NCERT Solutions Class 12 Maths Chapter 5 - Continuity & Differentiability
Description
Full syllabus notes, lecture & questions for NCERT Solutions Class 12 Maths Chapter 5 - Continuity & Differentiability - JEE | Plus excerises question with solution to help you revise complete syllabus | Best notes, free PDF download
Information about NCERT Solutions Exercise 5.3: Continuity & Differentiability
In this doc you can find the meaning of NCERT Solutions Exercise 5.3: Continuity & Differentiability defined & explained in the simplest way possible.
Besides explaining types of NCERT Solutions Exercise 5.3: Continuity & Differentiability theory,
EduRev gives you an ample number of questions to practice NCERT Solutions Exercise 5.3: Continuity & Differentiability tests, examples and also practice JEE tests.
Download as PDF
|
Explore Courses for JEE exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
shortcuts and tricks
,ppt
,Summary
,MCQs
,mock tests for examination
,NCERT Solutions Class 12 Maths Chapter 5 - Continuity & Differentiability
,NCERT Solutions Class 12 Maths Chapter 5 - Continuity & Differentiability
,Sample Paper
,Viva Questions
,Objective type Questions
,Important questions
,Extra Questions
,Previous Year Questions with Solutions
,Free
,NCERT Solutions Class 12 Maths Chapter 5 - Continuity & Differentiability
,Exam
,study material
,Semester Notes
,practice quizzes
,video lectures
,past year papers
;
Additional Information about NCERT Solutions Exercise 5.3: Continuity & Differentiability for JEE Preparation
NCERT Solutions Exercise 5.3: Continuity & Differentiability Free PDF Download
The NCERT Solutions Exercise 5.3: Continuity & Differentiability is an invaluable resource that delves deep into the core of the JEE exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the NCERT Solutions Exercise 5.3: Continuity & Differentiability now and kickstart your journey towards success in the JEE exam.
Importance of NCERT Solutions Exercise 5.3: Continuity & Differentiability
The importance of NCERT Solutions Exercise 5.3: Continuity & Differentiability cannot be overstated, especially for JEE aspirants.
This document holds the key to success in the JEE exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
NCERT Solutions Exercise 5.3: Continuity & Differentiability Notes
NCERT Solutions Exercise 5.3: Continuity & Differentiability Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to NCERT Solutions Exercise 5.3: Continuity & Differentiability.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, NCERT Solutions Exercise 5.3: Continuity & Differentiability Notes on EduRev are your ultimate resource for success.
NCERT Solutions Exercise 5.3: Continuity & Differentiability JEE Questions
The "NCERT Solutions Exercise 5.3: Continuity & Differentiability JEE Questions" guide is a valuable resource for all aspiring students preparing for the
JEE exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study NCERT Solutions Exercise 5.3: Continuity & Differentiability on the App
Students of JEE can study NCERT Solutions Exercise 5.3: Continuity & Differentiability alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the NCERT Solutions Exercise 5.3: Continuity & Differentiability,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of NCERT Solutions Exercise 5.3: Continuity & Differentiability is prepared as per the latest JEE syllabus.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup