NCERT Solutions Class 11 Maths Chapter 14 - Probability
Question 1:
Given that E and F are events such that P(E) = 0.6, P(F) = 0.3 and P(E ∩ F) = 0.2, find P (E|F) and P(F|E).
Answer 1:
It is given that P(E) = 0.6, P(F) = 0.3, and P(E ∩ F) = 0.2
Question 2:
Compute P(A|B), if P(B) = 0.5 and P (A ∩ B) = 0.32
Answer 2:
It is given that P(B) = 0.5 and P(A ∩ B) = 0.32
Question 3:
If P(A) = 0.8, P(B) = 0.5 and P(B|A) = 0.4, find
(i) P(A ∩ B) (ii) P(A|B) (iii) P(A ∪ B)
Answer 3:
It is given that P(A) = 0.8, P(B) = 0.5, and P(B|A) = 0.4
(i) P (B|A) = 0.4
Question 4:
Evaluate P (A ∪ B), if 2P (A) = P (B) = 5/13 and P(A|B) = 2/5
Answer 4:
Question 5:
If P(A) = 6/11, P(B) =5/11 and P(A ∪ B) =7/11 , find
(i) P(A ∩ B) (ii) P(A|B) (iii) P(B|A)
Answer 5:
It is given that
Question 6:
A coin is tossed three times, where
(i) E: head on third toss, F: heads on first two tosses
(ii) E: at least two heads, F: at most two heads
(iii) E: at most two tails, F: at least one tail
Answer 6:
If a coin is tossed three times, then the sample space S is
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
It can be seen that the sample space has 8 elements.
(i) E = {HHH, HTH, THH, TTH}
F = {HHH, HHT}
 E ∩ F = {HHH}
E ∩ F = {HHH}
(ii) E = {HHH, HHT, HTH, THH}
F = {HHT, HTH, HTT, THH, THT, TTH, TTT}
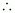 E ∩ F = {HHT, HTH, THH}
E ∩ F = {HHT, HTH, THH}
(iii) E = {HHH, HHT, HTT, HTH, THH, THT, TTH}
F = {HHT, HTT, HTH, THH, THT, TTH, TTT}
Question 7:
Two coins are tossed once, where
(i) E: tail appears on one coin, F: one coin shows head
(ii) E: not tail appears, F: no head appears
Answer 7:
If two coins are tossed once, then the sample space S is
S = {HH, HT, TH, TT}
(i) E = {HT, TH}
F = {HT, TH}
(ii) E = {HH}
F = {TT}
∴ E ∩ F = Φ
P (F) = 1 and P (E ∩ F) = 0
∴ P(E|F) =
Question 8:
A die is thrown three times,
E: 4 appears on the third toss, F: 6 and 5 appears respectively on first two tosses
Answer 8:
If a die is thrown three times, then the number of elements in the sample space will be 6 × 6 × 6 = 216
Question 9:
Mother, father and son line up at random for a family picture
E: son on one end, F: father in middle
Answer 9:
If mother (M), father (F), and son (S) line up for the family picture, then the sample space will be
S = {MFS, MSF, FMS, FSM, SMF, SFM}
⇒ E = {MFS, FMS, SMF, SFM}
F = {MFS, SFM}
∴ E ∩ F = {MFS, SFM}
Question 10:
A black and a red dice are rolled.
(a) Find the conditional probability of obtaining a sum greater than 9, given that the black die resulted in a 5.
(b) Find the conditional probability of obtaining the sum 8, given that the red die resulted in a number less than 4.
Answer 10:
Let the first observation be from the black die and second from the red die.
When two dice (one black and another red) are rolled, the sample space S has 6 × 6 = 36 number of elements.
Let A: Obtaining a sum greater than 9
= {(4, 6), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6)}
B: Black die results in a 5.
= {(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)}
∴ A ∩ B = {(5, 5), (5, 6)}
The conditional probability of obtaining a sum greater than 9, given that the black die resulted in a 5, is given by P (A|B).
(b) E: Sum of the observations is 8.
= {(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)}
F: Red die resulted in a number less than 4.
The conditional probability of obtaining the sum equal to 8, given that the red die resulted in a number less than 4, is given by P (E|F).
Question 11:
A fair die is rolled. Consider events E = {1, 3, 5}, F = {2, 3} and G = {2, 3, 4, 5}
Find (i) P (E|F) and P (F|E) (ii) P (E|G) and P (G|E) (ii) P ((E ∪ F)|G) and P ((E ∩ G)|G)
Answer 11:
When a fair die is rolled, the sample space S will be
S = {1, 2, 3, 4, 5, 6}
It is given that E = {1, 3, 5}, F = {2, 3}, and G = {2, 3, 4, 5}
(ii) E ∩ G = {3, 5}
(iii) E ∪ F = {1, 2, 3, 5}
(E ∪ F) ∩ G = {1, 2, 3, 5} ∩{2, 3, 4, 5} = {2, 3, 5}
E ∩ F = {3}
(E ∩ F) ∩ G = {3}∩{2, 3, 4, 5} = {3}
Question 12:
Assume that each born child is equally likely to be a boy or a girl. If a family has two children, what is the conditional probability that both are girls given that (i) the youngest is a girl, (ii) at least one is a girl?
Answer 12:
Let b and g represent the boy and the girl child respectively. If a family has two children, the sample space will be
S = {(b, b), (b, g), (g, b), (g, g)}
Let A be the event that both children are girls.
(i) Let B be the event that the youngest child is a girl.
The conditional probability that both are girls, given that the youngest child is a girl, is given by P (A|B).
Therefore, the required probability is (1/2).
(ii) Let C be the event that at least one child is a girl.
The conditional probability that both are girls, given that at least one child is a girl, is given by P(A|C).
Question 13:
An instructor has a question bank consisting of 300 easy True/False questions, 200 difficult True/False questions, 500 easy multiple choice questions and 400 difficult multiple choice questions. If a question is selected at random from the question bank, what is the probability that it will be an easy question given that it is a multiple choice question?
Answer 13:
The given data can be tabulated as
True/False | Multiple choice | Total | |
Easy | 300 | 500 | 800 |
Difficult | 200 | 400 | 600 |
Total | 500 | 900 | 1400 |
Let us denote E = easy questions, M = multiple choice questions, D = difficult questions, and T = True/False questions
Total number of questions = 1400
Total number of multiple choice questions = 900
Therefore, probability of selecting an easy multiple choice question is
P (E ∩ M) = 500/1400= 5/14
Probability of selecting a multiple choice question, P (M), is 900/1400= 9/14
P (E|M) represents the probability that a randomly selected question will be an easy question, given that it is a multiple choice question.
Therefore, the required probability is 5/9
Question 14:
Given that the two numbers appearing on throwing the two dice are different. Find the probability of the event ‘the sum of numbers on the dice is 4’.
Answer 14:
When dice is thrown, number of observations in the sample space = 6 × 6 = 36
Let A be the event that the sum of the numbers on the dice is 4 and B be the event that the two numbers appearing on throwing the two dice are different.
∴ A = {(1, 3), (2, 2), (3, 1)}
Let P (A|B) represent the probability that the sum of the numbers on the dice is 4, given that the two numbers appearing on throwing the two dice are different.
Question 15:
Consider the experiment of throwing a die, if a multiple of 3 comes up, throw the die again and if any other number comes, toss a coin. Find the conditional probability of the event ‘the coin shows a tail’, given that ‘at least one die shows a 3’.
Answer 15:
The outcomes of the given experiment can be represented by the following tree diagram.
The sample space of the experiment is,
Let A be the event that the coin shows a tail and B be the event that at least one die shows 3.
Probability of the event that the coin shows a tail, given that at least one die shows 3, is given by P(A|B).
Therefore,
Question 16:
If
(A) 0 (B) (1/2)
(C) not defined (D) 1
Answer 16:
Therefore, P (A|B) is not defined.
Thus, the correct answer is C.
Question 17:
If A and B are events such that P (A|B) = P(B|A), then
(A) A ⊂ B but A ≠ B (B) A = B
(C) A ∩ B = Φ (D) P(A) = P(B)
Answer 17:
It is given that, P(A|B) = P(B|A)
Thus, the correct answer is D.
|
172 videos|503 docs|154 tests
|
FAQs on NCERT Solutions Class 11 Maths Chapter 14 - Probability
| 1. What is probability? |  |
| 2. How is probability calculated? |  |
| 3. What are the different types of probability? |  |
| 4. How can probability be used in real-life situations? |  |
| 5. What are the common misconceptions about probability? |  |






















