NCERT Solutions for Class 9 Science Chapter 8 - Force and Laws of Motion
| Table of contents |

|
| Page No. 91 |

|
| Page No. 97 |

|
| Page No. 98 |

|
| Page No. 99 |

|
Page No. 91
Q1. Which of the following has more inertia?
(a) A rubber ball and a stone of the same size?
(b) A bicycle and a train?
(c) A five-rupee coin and a one-rupee coin?
Ans: Inertia is the property of an object to resist a change in its state of motion.
More mass = More inertia
(a) A stone has more mass than a rubber ball of the same size. Therefore, the stone has more inertia.
(b) A train has much more mass than a bicycle. Therefore, the train has more inertia.
(c) A five-rupee coin is heavier than a one-rupee coin. Therefore, the five-rupee coin has more inertia.
Q2. In the following example, try to identify the number of times the velocity of the ball changes.
"A football player kicks a football to another player of his team who kicks the football towards the goal. The goalkeeper of the opposite team collects the football and kicks it towards a player of his own team".
Also identify the agent supplying the force in each case.
Ans: The velocity of the ball changes four times in the following ways:
(a) Player 1 changes the velocity by kicking it.
(b) Player 2 changes the velocity by kicking it to the goal.
(c) The goalkeeper changes the velocity by collecting the ball.
(d) The goalkeeper changes the velocity by kicking the ball.
Q3. Explain why some of the leaves may get detached from a tree if we vigorously shake its branches.
Ans: The leaves of the tree have inertia of rest. When the branch is shaken, it moves, but the leaves tend to be in a state of rest due to their inertia. Thus, they get detached from the tree.
Q4. Why do you fall in the forward direction when a moving bus apply brakes to stop and fall back when it accelerates from rest?
Ans:
- In a running bus, our speed is equal to the speed of the bus. As a moving bus brakes to a stop, the lower part of our body, which is in contact with the bus, comes to rest, but the upper part, due to inertia of motion, remains in the state of motion.

- Hence, we fall in the forward direction. When the bus accelerates from rest, the feet come into motion while the upper part of the body remains at rest due to the inertia of rest; hence, we fall backwards.
Page No. 97
Exercises
Q1. An object experiences a net-zero external unbalanced force. Is it possible for the object to be travelling with a non-zero velocity? If yes, state the conditions that must be placed on the magnitude and direction of the velocity. If no, provide a reason.
Ans: Yes, it is possible for an object to travel with a non-zero velocity even when it experiences a net-zero external unbalanced force. This occurs due to the object's inertia of motion. Here are the key points:
- If the object is already in motion on a smooth surface, it will continue to move at the same velocity despite the absence of external forces.
- Example: When you stop pedalling a bicycle, it gradually slows down and eventually stops due to friction acting against its motion. If there were no friction or air resistance, the bicycle would keep moving indefinitely.
Q2. When a carpet is beaten with a stick, dust comes out of it. Explain.
Ans: When a carpet is beaten with a stick, the following happens:
- The carpet is suddenly set into motion.
- Dust particles, due to their inertia, tend to remain at rest.
- This inertia causes the dust to be dislodged from the carpet.
As a result, the dust comes out when the carpet is struck.
Q3. Why is it advised to tie any luggage kept on the roof of a bus with a rope?
Ans: It is advised to tie any luggage kept on the roof of a bus with a rope for the following reasons:
- The luggage has inertia, meaning it resists changes in motion.
- As the bus moves, brakes, or turns, the luggage may shift or fall off.
- Tying it with a rope helps to secure it and prevent accidents.
Q4. A batsman hits a cricket ball, which then rolls on level ground. After covering a short distance, the ball comes to rest. The ball slows to a stop because
(a) the batsman did not hit the ball hard enough.
(b) Velocity is proportional to the force exerted on the ball.
(c) There is a force on the ball opposing the motion.
(d) There is no unbalanced force on the ball, so the ball would want to come to rest.
Ans: When the ball rolls on the flat surface of the ground, its motion is opposed by the force of friction (the friction arises between the ground and the ball). This frictional force eventually stops the ball. Therefore, the correct answer is (c).
If the surface of the level ground is lubricated (with oil or some other lubricant), the friction that arises between the ball and the ground will reduce, which will enable the ball to roll for a longer distance.
Q5. A truck starts from rest and rolls down a hill with a constant acceleration. It travels a distance of 400 m in 20 s. Find its acceleration. Find the force acting on it if its mass is 7 metric tonnes.
(Hint: 1 metric tonne = 1000 kg.)
Ans:
Initial velocity of truck (u) = 0
Time (t) = 20 s
Distance covered (S) = 400 m
Acceleration (a) =?
Mass of truck (m) 7 tonne = 7000 kg
Force on truck We know ; (F) =?
We know:
S = ut + 1/2 at2
400 = 0 × 20 + 1/2 × a × (20)2
400 = 200a
a = 2ms-2
Force on truck (F) = ma
= 7000 x 2
= 14000 N
Q6. A stone of 1 kg is thrown with a velocity of 20 ms-1 across the frozen surface of a lake and comes to rest after travelling a distance of 50 m. What is the force of friction between the stone and the ice?
Ans:
Mass, m = 1kg; Initial velocity, u = 20 ms-1;
Final velocity, v = 0;
distance travelled, s = 50 m
Acceleration, 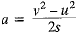
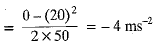
Force exerted = ma
= 1 kg x (- 4) ms-2 = - 4N
Friction = 4 N against the direction of motion.
Q7. An 8000 kg engine pulls a train of 5 wagons, each of 2000 kg, along a horizontal track. If the engine exerts a force of 40000 N and the track offers a friction force of 5000 N, then calculate:
(a) the net accelerating force and (b) the acceleration of the train
Ans: (a) Given, the force exerted by the train (F) = 40,000 N
The force of friction = -5000 N (the negative sign indicates that the force is applied in the opposite direction)
Therefore, the net accelerating force = the sum of all forces
= 40,000 N + (-5000 N)
= 35,000 N
(b) Total mass of the train = mass of engine + mass of each wagon = 8000kg + 5 × 2000kg
The total mass of the train is 18000 kg.
As per the second law of motion, F = ma (or: a = F/m)
Therefore, acceleration of the train = (net accelerating force) / (total mass of the train)
= 35,000/18,000 = 1.94 ms-2
The acceleration of the train is 1.94 ms-2
Q8. An automobile vehicle has a mass of 1500 kg. What must be the force between the vehicle and road if the vehicle is to be stopped with a negative acceleration of 1.7 ms-2?
Ans: Here, the mass of the automobile, m = 1,500 kg
Acceleration, a = 1.7 ms-2
Force between the vehicle and road (F) can be calculated as
F = ma = 1500 kg x ( -1.7 ms-2)
= -2,550 kg ms-2
= -2,550 N
Negative sign indicates that the force is in a direction opposite to the motion of the vehicle.
Page No. 98
Q9. What is the momentum of an object of mass m, moving with a velocity v?
(a) (mv)2
(b) mv2
(c) 1/2mv2
(d) mv
Ans: (d) mass x velocity
The momentum of an object is defined as the product of its mass m and velocity v.
Momentum = mass x velocity
Hence, the correct answer is mv, i.e., option (d).
Q10. Using a horizontal force of 200 N, we intend to move a wooden cabinet across a floor at a constant velocity. What is the friction force that will be exerted on the cabinet?
Ans: When a horizontal force of 200 N is applied to move a wooden cabinet at a constant velocity, the following occurs:
- The cabinet's acceleration is zero because its velocity remains constant.
- This means the net force acting on the cabinet is also zero.
- Consequently, the frictional force opposing the motion must equal the applied force.
- Thus, the friction force exerted on the cabinet is 200 N.
In summary, the total friction force is -200 N, indicating it acts in the opposite direction to the applied force.
Q11. According to the third law of motion, when we push on an object, the object pushes back on us with an equal and opposite force. If the object is a massive truck parked along the roadside, it will probably not move. A student justifies this by answering that the two opposite and equal forces cancel each other. Comment on this logic and explain why the truck does not move.
Ans: The student's logic is incorrect because the action and reaction forces do not cancel each other out; they act on different objects. Here’s why the truck does not move:
- The truck is massive, giving it a large inertia, which resists changes in motion.
- It is parked on the ground, where a frictional force exists between the truck and the surface.
- The applied force is insufficient to overcome the static friction between the truck and the road.
- As a result, the forces are balanced: the force we exert plus the frictional force equals zero, leading to no movement.
Q12. A hockey ball of mass 200 g travelling at 10 ms-1 is struck by a hockey stick so as to return it along its original path with a velocity at 5 ms-1. Calculate the change of momentum that occurred in the motion of the hockey ball due to the force applied by the hockey stick.
Ans:
Mass of ball (m) = 200 g = 0.2 kg
Initial velocity of ball (u1) = 10 ms-1
Final velocity of ball (u2) = 5 ms-1
(Negative sign denotes that the ball is moving in the opposite direction)
Initial momentum of ball = mu1 = 0.2 × 10 = 2 Ns
Final momentum of ball = mu2 = 0.2 × (- 5) = -1 Ns
Change in momentum = Final momentum - Initial momentum
= -1 - 2 Ns = -3 Ns
Negative sign denotes that change in momentum is in the direction opposite to the direction of initial momentum of the ball.
Q13. A bullet of mass 10g travelling horizontally with a velocity of 150 ms-1 strikes a stationary wooden block and comes to rest in 0.03s. Calculate the distance of penetration of the bullet into the block. Also, calculate the magnitude of the force exerted by the wooden block on the bullet.
Ans:
Mass of bullet (m) = 10 g = 0.01 kg
The initial velocity of a bullet (u) = 150 ms-1
The final velocity of a bullet (v) = 0
Time (t) = 0.03 secs
Acceleration on the bullet (a) =?
Force acting on wooden block (F) =?
Distance penetrated by the bullet (s) =?
We know:
v = u + at
0 = 150 + (a × 0.3)
a × 0.03 = -150
a = -5000 ms-2 (Negative sign indicates that the velocity of the bullet is decreasing.)
We know:
S = ut + 0.5at2
s = 150 × 0.03 + (-5000) × (0.03)2 = 4.5 - 2.25 = 2.25m
We know:
F = ma
Force acting on bullet (F) = ma = 0.01 × (-5000) = -50N
Negative sign denotes that wooden block exerts force in the direction, opposite to the direction of motion of the bullet.
Q14. An object of mass 1 kg travelling in a straight line with a velocity of 10 ms-1 collides with and sticks to a stationary wooden block of mass 5 kg. Then they both move off together in the same straight line. Calculate the total momentum just before the impact and just after the impact. Also, calculate the velocity of the combined object.
Ans: For object:
m1 = 1 kg
u1 = 10 ms1
For wooden block:
m2 = 5 kg
u2 = 0
Momentum just before collision:
= m1u1 + m2u2
= 1 × 10 + 5 × 0
= 10 kg ms-1
Mass after collision = (m1 + m2)
= 1 + 5 = 6 kg
Let velocity after collision = v
Momentum after collision = 6 × v
Using the law of conservation of momentum:
Momentum after collision = Momentum before collision
6 × v = 10
v = 1.67 ms-1
Q15. An object of mass 100 kg is accelerated uniformly from a velocity of 5 ms-1 to 8 ms-1 in 6s. Calculate the initial and final momentum of the object. Also, find the magnitude of the force exerted on the object.
Ans:
Mass of object (m) = 100 kg
Initial velocity (u) = 5 ms-1
Final velocity (v) = 8 ms-1
Time (t) = 6 s
Initial momentum (Pinitial) = mu = 100 × 5 = 500 Ns
Final momentum (Pfinal) = mv = 100 × 8 = 800 Ns
Force exerted on the object (F) = [(mv - mu) / t] = (800 - 500)/6 = 300/6 = 50N
Q16. Akhtar, Kiran and Rahul were riding in a motorcar that was moving with a high velocity on an expressway when an insect hit the windshield and got stuck on the windscreen. Akhtar and Kiran started pondering over the situation. Kiran suggested that the insect suffered a greater change in momentum as compared to the change in momentum of the motorcar (because the change in the velocity of the insect was much more than that of the motorcar). Akhtar said that since the motorcar was moving with a larger velocity, it exerted a larger force on the insect. And as a result the insect died. Rahul while putting an entirely new explanation said that both the motorcar and the insect experienced the same force and a change in their momentum. Comment on these suggestions.
Ans: As per the law of conservation of momentum, the total momentum before the collision between the insect and the car is equal to the total momentum after the collision. Therefore:
- The change in momentum of the insect is much greater than that of the motorcar due to the insect's smaller mass.
Akhtar's assumption is partially correct:
- Since the mass of the car is very high, the force exerted on the insect during the collision is also very high.
Kiran's statement is incorrect:
- The change in momentum of the insect and the motorcar is equal, as stated by the conservation of momentum.
- The insect's velocity changes significantly due to its small mass compared to the motorcar.
- Conversely, the motorcar's velocity change is negligible because of its large mass.
Rahul's statement is partially correct:
- According to the third law of motion, the force exerted by the insect on the car is equal and opposite to the force exerted by the car on the insect.
- However, his claim that the change in momentum is the same contradicts the law of conservation of momentum.
Q17. How much momentum will a dumbbell of mass 10 kg transfer to the floor if it falls from a height of 80 cm and does not rebound? Take its downward acceleration to be 10ms-2.
Ans:
Height, h = 80 cm = 0.8 m
Mass, m = 10 kg ; Initial velocity, u = 0
Acceleration, a = 10 ms-2
Final velocity, v = 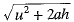
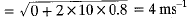
Momentum transferred = mv = 10 kg x 4 ms-1
= 10 kg x 4 ms-1
= 40 kgms-1
Page No. 99
Q1. The following is the distance-time table of an object in motion:
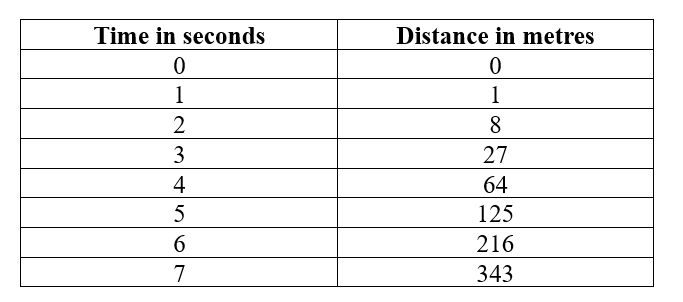
(a) What conclusion can you draw about the acceleration? Is it constant, increasing, decreasing or zero?
(b) What do you infer about the forces acting on the object?
Ans:
(a) The distance covered by the object at any time interval is greater than any of the distances covered in previous time intervals. Therefore, the acceleration of the object is increasing.
(b) Force, F = ma ⇒ F ∝ a. Since the mass of the object remains constant, the increasing acceleration implies that the force acting on the object is increasing as well
Q2. Two persons manage to push a motorcar of mass 1200 kg at a uniform velocity along a level road. The same motorcar can be pushed by three persons to produce an acceleration of 0.2 ms-2. With what force does each person push the motorcar? (Assume that all persons push the motorcar with the same muscular effort.)
Ans:
Mass of car, m = 1200 kg
Let each person apply force F on the motor car. Thus, the force 2F applied by 2 persons balances the frictional force due to the ground force applied by three persons = 3F
Effective force = 3F - friction = 3F - 2F = F
Thus, force F produces an acceleration of 0.2 ms-2.
F = ma = 1200 x 0.2 = 240 N
Thus,the force applied by each person = 240 N
Q3. A hammer of mass 500 g, moving at 50 ms-1, strikes a nail. The nail stops the hammer in a very short time of 0.01 s. What is the force of the nail on the hammer?
Ans:
Mass of hammer, M = 500 g = 0.5 kg
The initial velocity of the hammer, u = 50 ms-1
The final velocity of the hammer, v = 0
Time, t = 0.01 s = - 5000 ms-2
= - 5000 ms-2
The force applied by the nail, F = ma
= (0.5) x (-5000 ms-2)
= - 2500 N (opposite to the motion of the hammer)
Q4. A motorcar of mass 1200 kg is moving along a straight line with a uniform velocity of 90 km/h. Its velocity is slowed down to 18 km/h in 4 s by an unbalanced external force. Calculate the acceleration and change in momentum. Also calculate the magnitude of the force required.
Ans:
Mass of motor car, m = 1200 kg
Initial velocity of car, u = 90 km/h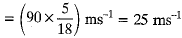
Final velocity of car, v = 18 km/h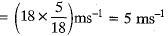
Time, t = 4s
Acceleration, 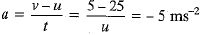
Momentum change = mv - mu or m(v - u)
= 1200 (5 - 25) = - 24000 kg ms-1
Magnitude of force, F = ma
= 1200 x (- 5) = - 6000 N
Acceleration, momentum change and force are opposing the motion of the motorcar, as indicated by a negative sign.
|
84 videos|478 docs|60 tests
|
FAQs on NCERT Solutions for Class 9 Science Chapter 8 - Force and Laws of Motion
| 1. What is Newton's First Law of Motion? |  |
| 2. How does mass affect inertia? |  |
| 3. What is the difference between balanced and unbalanced forces? |  |
| 4. Can you explain the concept of friction and its types? |  |
| 5. How do action and reaction forces work according to Newton's Third Law? |  |
















