NCERT Solutions for Class 9 Maths - Introduction to Euclid’s Geometry (Exercise 5.1)
Q1: Which of the following statements are true and which are false? Give reasons for your answers.
(i) Only one line can pass through a single point.
(ii) There are an infinite number of lines which pass through two distinct points.
(iii) A terminated line can be produced indefinitely on both the sides
(iv) If two circles are equal, then their radii are equal.
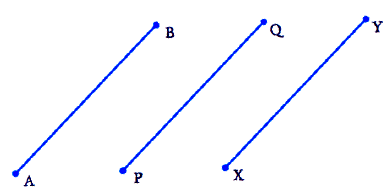
(v) In the following figure, if AB = PQ and PQ = XY, then AB = XY.
Ans: (i) False
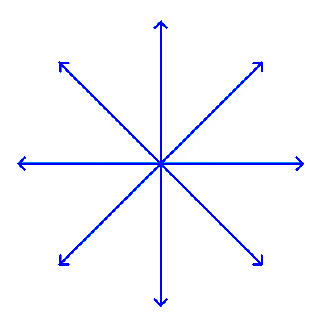
Reason: Through a single point ‘P’ below, an infinite number of lines can pass. In the following figure, it can be seen that there are infinite numbers of lines passing through a single point P.
(ii) False
Reason:Since through two distinct points, only one line can pass. In the following figure, it can be seen that there is only one single line that can pass through two distinct points P and Q.

(iii) True
Reason: A terminated line can be produced indefinitely on both sides. Let AB be a terminated line. It can be seen that it can be produced indefinitely on both sides.

(iv) True
Reason: If two circles are equal, then their centre and circumference will coincide and hence, the radii will also be equal.
(v) True
Reason:
It is given that AB and XY are two terminated lines (Line Segments) and both are equal to a third line PQ.
Euclid’s first axiom states that things which are equal to the same thing are equal to one another.
Therefore, the lines AB =PQ and PQ = XY, Hence AB = XY will be equal to each other.
Q2: Give a definition for each of the following terms. Are there other terms that need to be defined first? What are they, and how might you define them?
(i) parallel lines
(ii) perpendicular lines
(iii) line segment
(iv) radius of a circle
(v) square
Ans: Yes, we need to have an idea about the terms, point, line, ray, angle, plane, circle and quadrilateral, etc. before defining the required terms.
Point: A small dot made by a sharp pencil on the surface of paper gives an idea about a point.
It has no dimensions. It has only a position.
Line: A line is an idea that it should be straight and that it should extend indefinitely in both directions. It has no endpoints and has no definite length.
Note: In geometry, a line means “The line in its totality and not a portion of it. Whereas a physical example of a perfect line is not possible. A line extends indefinitely in both directions, so we cannot draw or show it wholly on paper. That is why we mark arrowheads on both ends, indicating that it extends indefinitely in both directions.
Ray: A part of a line that has only one endpoint and extends indefinitely in one direction. A ray has no definite length.
Angle: Two rays having a common endpoint form an angle.
Plane: A plane is a surface such that every point of the line joining any two points on it, lies on it.
Circle: A circle is the set of all those points in a given plane that are equidistant from a fixed point in the same plane. The fixed point is called the centre of the circle.
Quadrilateral: A closed figure made of four line segments is called a quadrilateral.
Definitions of the required terms are given below:
(i) Parallel Lines:
- If the perpendicular distance between two lines is always constant, then these are called parallel lines.
- In other words, the lines which never intersect each other are called parallel lines.
- To define parallel lines, we must know about point, lines, and distance between the lines and the point of intersection.
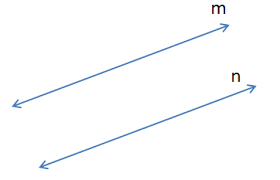
Note: The distance between two parallel lines always remains the same.
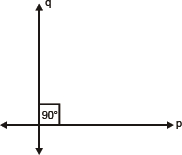
(ii) Perpendicular Lines:
- If two lines intersect each other at 90∘ , then these are called perpendicular lines.
- We are required to define line and the angle before defining perpendicular lines.
(iii) Line Segment: A line segment is a part of the line having a definite length. It has two end-points.
In the figure, a line segment is shown having endpoints ‘A’ and ‘B’. It is written as or
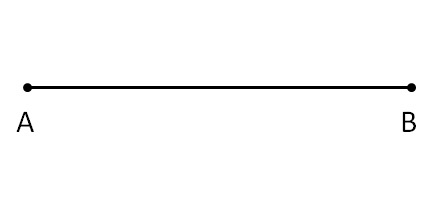
(iv) Radius of a circle:
- It is the distance between the centers of a circle to any point lying on the circle.
- To define the radius of a circle, we must know about point and circle.
(v) Square: A quadrilateral in which all the four angles are right angles and all the four sides are equal is called a square. In the figure, PQRS is a square.
Q3. Consider two ‘postulates’ given below:
(i) Given any two distinct points A and B, there exists a third point C which is in between A and B.
(ii) There exist at least three points that are not on the same line.
Do these postulates contain any undefined terms? Are these postulates consistent?
Do they follow Euclid’s postulates? Explain.
Ans: Yes, these postulates contain undefined terms. Undefined terms in the postulates are
- There are many points that lie in a plane. But, in the postulates given here, the position of point C is not given as to whether it lies on the line segment joining AB or not.
- On top of that, there is no information about whether the points are in the same plane or not.
And
Yes, these postulates are consistent when we deal with these two situations:
- Point C is lying on the line segment AB in between A and B.
- Point C does not lie on line segment AB.
No, they don’t follow Euclid’s postulates. They follow the axioms.
Q4. If a point C lies between two points A and B such that AC = BC, then prove that AC = (1/2)AB. Explain by drawing the figure.
Ans: 
Given that, AC = BC
Now, adding AC on both sides,
L.H.S.+AC = R.H.S.+AC
AC+AC = BC+AC
2AC = BC+AC
We know that BC+AC = AB (as it coincides with line segment AB)
∴ 2 AC = AB (If equals are added to equals, the wholes are equal.)
⇒ AC = (½)AB
Q5. In Question 4, point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.
Ans:
From the figure,
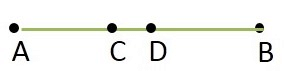
Given,
Let there be two mid-points, C and D.
C is the mid-point of AB.
To Prove:
Every line segment has one and only one mid-point.
Proof:
Let us assume, D be another mid- point of AB.
Therefore AD = DB ... Equation (1)
But it is given that C is the mid- point of AB.
Therefore AC = CB ... Equation (2)
Subtracting Equation (1) from Equation (2) we get
AC – AD = CB – DB
DC = – DC
2 DC = 0
DC = 0
Therefore C and D coincide.
Thus, every line segment has one and only one mid- point.
Q6. In the figure, given below, if AC = BD, then prove that AB = CD.
Ans:

It is given AC = BD
From the given figure, we get
AC = AB+BC
BD = BC+CD
⇒ AB+BC = BC+CD [AC = BD, given]
We know that, according to Euclid’s axiom, when equals are subtracted from equals, remainders are also equal.
Subtracting BC from the L.H.S. and R.H.S. of the equation AB+BC = BC+CD, we get
AB+BC-BC = BC+CD-BC
AB = CD
Hence, proved.
Q7. Why is Axiom 5, in the list of Euclid’s axioms, considered a ‘universal truth’? (Note that the question is not about the fifth postulate.)
Ans:
Axiom 5 states that the whole is greater than the part.
This axiom is known as a universal truth because it holds true in any field, and not just in the field of mathematics.
Let us take two cases – one in the field of mathematics, and one other than that.
Case I:
a. Let t represent a whole quantity and only a, b, c are parts of it.
b. t = a + b + c Clearly, t will be greater than all its parts a, b, and c.
c. Therefore, it is rightly said that the whole is greater than the part.
Case II:
a. Let us consider the continent Asia.
b. Then, let us consider a country India which belongs to Asia.
c. India is a part of Asia and it can also be observed that Asia is greater than India.
d. That is why we can say that the whole is greater than the part.
e. This is true for anything in any part of the world and is thus a universal truth.
|
40 videos|471 docs|57 tests
|
FAQs on NCERT Solutions for Class 9 Maths - Introduction to Euclid’s Geometry (Exercise 5.1)
| 1. What is Euclid's Geometry? |  |
| 2. What are the axioms in Euclid's Geometry? |  |
| 3. How is Euclid's Geometry different from non-Euclidean geometry? |  |
| 4. What are the main components of Euclid's Geometry? |  |
| 5. How is Euclid's Geometry relevant in today's world? |  |

















