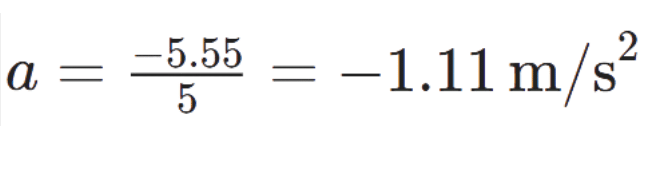NCERT Solutions for Class 9 Science Chapter 7 - Motion
| Table of contents |

|
| Page No. 74 |

|
| Page No. 76 |

|
| Page No. 77 |

|
| Page No. 81 |

|
| Page No. 82 |

|
| Page No. 83 |

|
| Page No. 85 |

|
| Page No. 86 |

|
| Activity-Based Questions |

|
Page No. 74
Q1. An object has moved through a distance. Can it have zero displacements? If yes, support your answer with an example.
Ans: Yes. An object can have zero displacement even after moving.
Example: An athlete runs around a circular track and returns to the starting point.
Distance = 2πr
Displacement = 0
Q2. A farmer moves along the boundary of a square field of side 10 m in the 40s. What will be the magnitude of displacement of the farmer at the end of 2 minutes 20 seconds from his initial position?
Ans: Given,
- Side of the square field = 10 m
- Perimeter of the square = 4 × 10 = 40 m
- Time to complete one round = 40 s
- Total time = 2 minutes 20 seconds = 2 × 60 + 20 = 140 s
Speed of the farmer = Perimeter / Time = 40 / 40 = 1 m/s
Distance covered in 140 s = 1 × 140 = 140 m
Number of complete rounds = Total distance / Perimeter = 140 / 40 = 3.5
After 3 complete rounds (120 m, 120 s), the farmer is back at the starting point (e.g., point A at (0,0)). In the remaining 0.5 round (20 m, 20 s), the farmer moves halfway around the square. Starting at A (0,0), the path is:
- A to B (10,0): 10 m
- B to C (10,10): 10 m
After 0.5 round, the farmer is at C (10,10). The displacement is the straight-line distance from A (0,0) to C (10,10):
Displacement = √((10-0)² + (10-0)²) = √(100 + 100) = √200 = 10√2 ≈ 14.14 m
Magnitude of displacement = 14.14 m
Q3. Which of the following is true for displacement?
(a) It cannot be zero.
(b) Its magnitude is greater than the distance travelled by the object.
Ans:
(a) False; Displacement can be zero if an object returns to its initial position after moving. For example, an athlete running around a circular track and returning to the starting point has zero displacement.
(b) False; The magnitude of displacement is always less than or equal to the distance travelled. Displacement equals distance only when the motion is in a straight line without reversing direction. For example, in circular motion, displacement is zero when returning to the start, while distance is non-zero.
Page No. 76
Q1. Distinguish between speed and velocity.
Ans:

Q2. Under what condition(s) is the magnitude of the average velocity of an object equal to its average speed?
Ans: Average speed measures the total distance covered over a specific time period, while average velocity refers to the total displacement during that same time. The magnitudes of average speed and average velocity will be equal when the total distance traveled matches the displacement.
Q3. What does the odometer of an automobile measure?
Ans: An odometer, also known as an odograph, is a device that calculates the distance an automobile has travelled by measuring the circumference of the wheel as it rotates.
Q4. What does the path of an object look like when it is in uniform motion?
Ans: In uniform motion, the object moves in a straight line, covering equal distances in equal intervals of time.
Q5. During an experiment, a signal from a spaceship reached the ground station in five minutes. What was the distance of the spaceship from the ground station? The signal travels at the speed of light, which is 3 × 108 ms-1.
Ans: Speed of signal = 3 × 108 ms-1
Time in which signal reaches ground = 5 min = 5 × 60 = 300 s
Distance of spaceship from the ground level = speed × time = 3 × 108 × 300 = 9 × 1010 m
Page No. 77
Q1. When will you say a body is in
(i) Uniform acceleration (ii) Non-uniform acceleration?
Ans:
(i) If an object travels in a straight line and its velocity increases or decreases by equal amounts in equal intervals of time, then the body is said to be in uniform acceleration.
Example: The motion of a freely falling body.
(ii) If an object travels in a straight line and its velocity changes by unequal amounts in equal intervals of time, then the body is said to be in non-uniform acceleration.
Example: If a car is travelling along a straight road and passes through a crowd, suffers an unequal change in velocity, in equal intervals of time.
Q2. A bus decreases its speed from 80 km h−1 to 60 km h−1 in 5 s. Find the acceleration of the bus.
Ans:
- Initial velocity, u=80km/h
- Final velocity, v=60km/h
- Time, t=5s
Solution:
- Convert velocities from km/h to m/s:
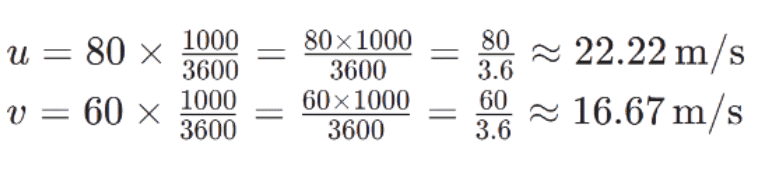
Use the first equation of motion: v=u+at
The acceleration of the bus is −1.11m/s2 (negative sign indicates deceleration or retardation).
Q3. A train starting from a railway station and moving with uniform acceleration attains a speed of 40 km h-1 in 10 minutes. Find its acceleration.
Ans: Given,
Initial velocity, u = 0 km /h
Final velocity, v = 40 km/h =40 × ( 5/ 18) = 11.11 m/s
Time, t = 10 min = 10 × 60 = 600 sec
Acceleration, a = ?
Consider the formula, v = u + at
⇒ 11.11 = 0 + a × 600
⇒ 11.11 = 600 a
⇒ a = 11.11/600 = 0.0185 m/s2
Page No. 81
Q1. What is the nature of the distance-time graphs for uniform and non-uniform motion of an object?
Ans:
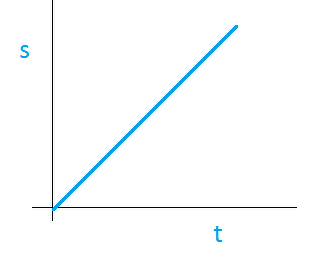
- When the motion is uniform, the distance-time graph is a straight line with a slope.
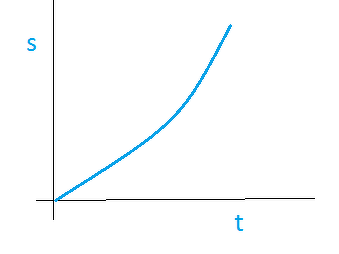
- When the motion is non-uniform, the distance-time graph is not a straight line. It can be any curve.
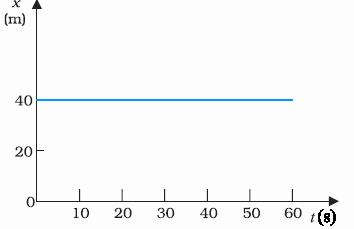
Q2. What can you say about the motion of an object whose distance-time graph is a straight line parallel to the time axis?
Ans: If the distance-time graph is a straight line parallel to the time axis, the body is at rest.
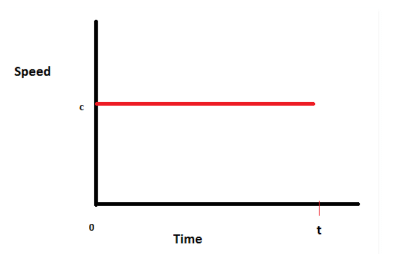
Q3. What can you say about the motion of an object if its speed-time graph is a straight line parallel to the time axis?
Ans: If the speed-time graph is a straight line parallel to the time axis, the object is moving uniformly.
Q4. What is the quantity which is measured by the area occupied below the velocity-time graph?
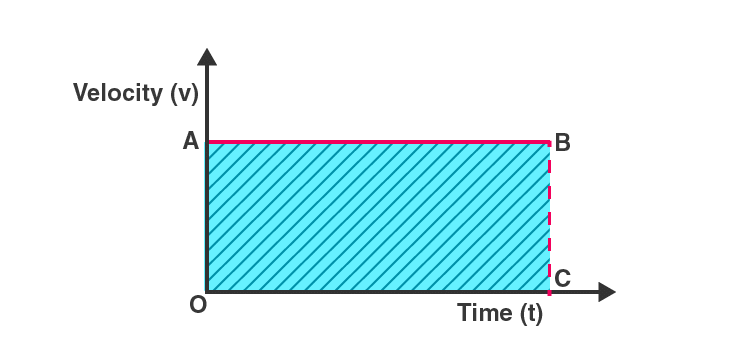
Ans: The area beneath the velocity-time graph corresponds to the area of the rectangle OABC, calculated as OA multiplied by OC. Here, OA represents the object's velocity, and OC indicates time. Thus, the shaded area can be expressed as:
The area under the velocity-time graph = velocity × time.
By substituting the value of velocity as displacement divided by time into this equation, we find that the area under the velocity-time graph represents the total displacement of the object.
Page No. 82
Q1. A bus starting from rest moves with a uniform acceleration of 0.1 m s-2 for 2 minutes. Find
(a) the speed acquired, (b) the distance travelled.
Ans: Given,
Initial velocity, u = 0 ms-1
Acceleration, a = 0.1 ms-2
Time, t = 2 min = 120 s
(a) Speed, v = u + at = 0 + 0.1 x 120 = 12 ms-1
(b) Distance, s 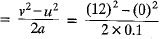 = 720 m
= 720 m
The speed acquired is 12 ms-1 and the total distance travelled is 720 m.
Q2. A train is travelling at a speed of 90 km h-1. Brakes are applied so as to produce a uniform acceleration of 0.5 ms-2. Find how far the train will go before it is brought to rest.
Ans: Given the initial speed of the train, u= 90 km/h = 25 m/s
Final speed of the train, v = 0 m/s (finally the train comes to rest)
Acceleration = - 0.5 m s-2
According to the third equation of motion:
v2 = u2 + 2as (where s is the distance covered by the train)
⇒ (0)2 = (25)2 + 2 (- 0.5) s
⇒ 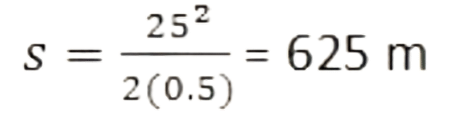
The train will cover a distance of 625 m at an acceleration of -0.5ms-2 before it comes to rest.
Q3. A trolley, while going down an inclined plane, has an acceleration of 2 cm/s-2. What will be its velocity 3 s after the start?
Ans: Initial Velocity of trolley, u = 0 cms-1; Acceleration, a = 2 cms-2; Time, t = 3 s
We know that final velocity, v = u + at = 0 + 2 x 3 cms-1
Therefore, The velocity of the trolley after 3 seconds = 6 cms-1
Page No. 83
Q4. A racing car has a uniform acceleration of 4 ms-2. What distance will it cover in 10 s after the start?
Ans: Initial Velocity of the car, u = 0 ms-1; Acceleration, a = 4 m s-2; Time, t = 10 s
We know Distance, s = ut + (1/2) at2
Therefore, Distance covered by car in 10 second = 0 × 10 + (1/2) × 4 × 102 = (1/2) × 400 = 200 m
Q5. A stone is thrown in a vertically upward direction with a velocity of 5 m/s-1. If the acceleration of the stone during its motion is 10 m/s-2 in the downward direction, what will be the height attained by the stone and how much time will it take to reach there?
Ans: Given,
The initial velocity of stone, u = 5 ms-1
Downward or negative acceleration, a = 10 ms-2
We know that: 2as = v2- u2
⇒ 0 = (5)2 + 2 x(-10) x s
⇒ 0 = 25 - 20s
⇒ s = 25/20 = 1.25 m
The height attained by stone, s = 1.25 m
We know that: v = u + at
⇒ 0 = 5 + (–10) × t
⇒ 0 = 5 − 10t
⇒ t = 5/10 = 0.5 s
Thus, the stone will attain a height of 1.25 m and the time taken to attain the height is 0.5 s.
Page No. 85
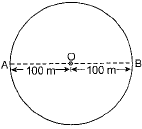
Q1. An athlete completes one round of a circular track of diameter 200 m in 40 s. What will be the distance covered and the displacement at the end of 2 minutes 20 s?
Ans: Here, the diameter of the circular track = 200 m.
The radius of the circular track, r = 100 m.
Let the athlete start moving from A, which is treated as a reference point.
Given:
- Diameter of the circular track = 200 m
- Radius, r = 100 m
- Time for one round = 40 s
- Total time = 2 minutes 20 seconds = 2 × 60 + 20 = 140 s
Circumference of the track = 2πr = 2 × (22/7) × 100 = 4400/7 ≈ 628.57 m
Speed = Circumference / Time = 628.57 / 40 ≈ 15.71 m/s
Distance covered in 140 s = 15.71 × 140 ≈ 2200 m
Number of rounds = Distance / Circumference = 2200 / 628.57 ≈ 3.5
After 3 complete rounds, the athlete is back at the starting point (e.g., point A). After 0.5 round more, the athlete is at the opposite point on the circular track (e.g., point B, 180° from A). Since the track has a diameter of 200 m, the displacement is the straight-line distance from A to B, which is the diameter:
Displacement = 200 m
Distance covered = 2200 m, Displacement = 200 m
Q2. Joseph jogs from one end A to the other end B of a straight 300 m road in 2 minutes 50 seconds and then turns around and jogs 100 m back to point C in another 1 minute. What are Joseph's average speeds and velocities in Jogging (a) from A to B and (b) from A to C?
Ans: Let Joseph jog from A to B and back to C as shown.
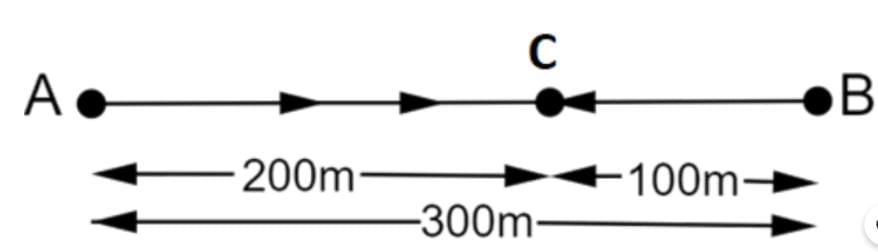
Given:
- A to B: Distance = 300 m, Time = 2 minutes 50 seconds = 2 × 60 + 50 = 170 s.
- B to C: Distance = 100 m (back toward A), Time = 1 minute = 60 s.
- A to C: Total distance = 300 m (A to B) + 100 m (B to C) = 400 m, Total time = 170 s + 60 s = 230 s.
- Displacement A to C: From A to B is 300 m in the positive direction; from B to C is 100 m in the negative direction. Net displacement = 300 m - 100 m = 200 m (in the positive direction, toward B).
Solution:
(a) From A to B:
Average Speed:
- Distance = 300 m, Time = 170 s.
- Average speed = Distance / Time = 300 / 170 ≈ 1.7647 m/s.
Average Velocity:
- Displacement = 300 m (positive direction, as motion is straight from A to B).
- Average velocity = Displacement / Time = 300 / 170 ≈ 1.7647 m/s (in the direction from A to B).
Average speed = 1.76 m/s, Average velocity = 1.76 m/s (toward B).
(b) From A to C:
Average Speed:
- Total distance = 400 m, Total time = 230 s.
- Average speed = Total distance / Total time = 400 / 230 ≈ 1.7391 m/s.
Average Velocity:
- Net displacement = 200 m (positive direction, as C is 200 m from A toward B).
- Average velocity = Displacement / Time = 200 / 230 ≈ 0.8696 m/s (in the direction from A to B).
Average speed = 1.74 m/s, Average velocity = 0.87 m/s (toward B).
Final Answer:
- (a) A to B: Average speed = 1.76 m/s, Average velocity = 1.76 m/s (toward B).
- (b) A to C: Average speed = 1.74 m/s, Average velocity = 0.87 m/s (toward B).
Activity-Based Questions
Activity 7.1
Q: Discuss whether the walls of your classroom are at rest or in motion.
Ans: The walls of the classroom appear to be at rest with respect to us because their position does not change relative to us or the classroom floor. However, if we observe with respect to the Sun or the Universe, the walls are in motion because the Earth itself is rotating on its axis and revolving around the Sun. So, the walls are at rest with respect to us, but in motion with respect to the Sun.
Activity 7.2
Q: Have you ever experienced that the train in which you are sitting appears to move while it is at rest? Discuss and share your experience.
Ans: Yes, I have experienced this situation. When two trains are standing side by side at a station and one of them starts moving slowly, it sometimes appears that our train is moving backward, even though it is actually at rest. This happens because we judge motion by comparing with nearby objects, and in this case, the other moving train creates an illusion of motion for our train.
Activity 7.3
Q: Take a metre scale and a long rope. Walk from one corner of a basketball court to its opposite corner along its sides.
Measure the distance covered by you and the magnitude of displacement.
What difference do you notice between the two?
Ans: Let the court have length = l and breadth = b.
Distance covered along the sides = l + b.
Magnitude of displacement = length of the diagonal = 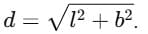
Since 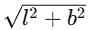 (for positive
(for positive
Example (basketball court 28 m × 15 m):
Distance =
Displacement = 
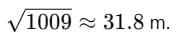
Activity 7.4
Q. An odometer shows the distance travelled by a car from Bhubaneswar to New Delhi as 1850 km. Using the Road Map of India, find the magnitude of displacement between Bhubaneswar and New Delhi.
Ans. Draw a straight line joining Bhubaneswar and New Delhi on the map and use the map’s scale to measure the straight-line (airline) distance. This gives a displacement of about 1,270 km (≈ 1.27 × 103 km).
Therefore: Distance travelled (odometer) = 1850 km; Displacement ≈ 1270 km. Displacement is less because it is the shortest straight-line distance, while road distance follows a longer, curved route.
Activity 7.5
Q: The data regarding the motion of two different objects A and B are given in Table 7.1. Examine them carefully and state whether the motion of the objects is uniform or non-uniform.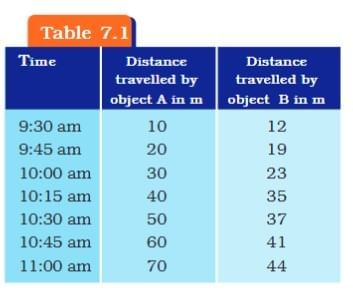
Ans:
Step 1 — Find distance covered in each 15-minute interval
Object A:
• 9:30–9:45:
• 9:45–10:00:
• 10:00–10:15:
• 10:15–10:30:
• 10:30–10:45:
• 10:45–11:00:
Object B:
• 9:30–9:45:
• 9:45–10:00:
• 10:00–10:15:
• 10:15–10:30:
• 10:30–10:45:
• 10:45–11:00:
Step 2 — Decide uniform or non-uniform
Object A: The distance covered in every equal time interval (15 min) is constant (10 m in each interval).
→ Therefore motion of A is uniform.
Object B: The distance covered in equal time intervals is not constant (7, 4, 12, 2, 4, 3 m).
→ Therefore motion of B is non-uniform.
(Optional: speeds in m/min for clarity)
Each interval = 15 min.
Speed of A =
Average speed of B over whole period = total gain
→
Activity 7.6
Q: Measure the time it takes you to walk from your house to your bus stop or the school. If your average walking speed is
Ans: We know,
Suppose it takes me 15 minutes (i.e.
Therefore, the bus stop is about 1 km away from my house.
Activity 7.7
Q: At a time when it is cloudy, there may be frequent thunder and lightning. The sound of thunder takes some time to reach you after you see the lightning.
Can you answer why this happens?
Measure this time interval using a stopwatch.
Calculate the distance of the nearest point of lightning. (Speed of sound in air =
Ans: We see lightning first and hear thunder later because light travels much faster than sound. Light from lightning reaches us almost instantly, while sound travels slowly through air at about 346m s−1.
Let the time interval between lightning and thunder (measured with a stopwatch) = t seconds.
Example:
If the time gap = 5 seconds, then
Distance = 346 × 5 = 1730 m ≈ 1.7 km
Therefore, the thunder is heard later because sound travels slower than light, and the distance of lightning can be calculated as 346 × t.
Activity 7.8
Q: In your everyday life you come across a range of motions in which
(a) acceleration is in the direction of motion,
(b) acceleration is against the direction of motion,
(c) acceleration is uniform,
(d) acceleration is non-uniform.
Can you identify one example each for the above type of motion?
Ans.
(a) Acceleration in the direction of motion – A car speeding up while moving on a straight road.
(b) Acceleration against the direction of motion – A moving bicycle being stopped by applying brakes.
(c) Uniform acceleration – A freely falling body under gravity (neglecting air resistance).
(d) Non-uniform acceleration – A car moving through heavy traffic, where its speed keeps changing irregularly.
Activity 7.9
Q: The times of arrival and departure of a train at three stations A, B, and C and the distance of stations B and C from station A are given in Table 7.4.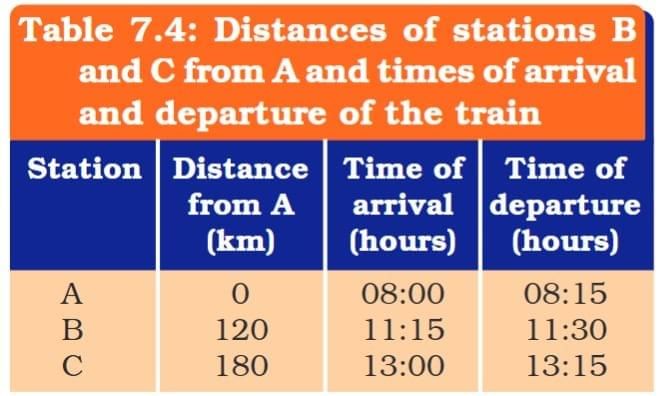
Plot and interpret the distance–time graph for the train assuming that its motion between any two stations is uniform.
Ans: Do it Yourself.
Activity 7.10
Q: Feroz and his sister Sania go to school on their bicycles. Both of them start at the same time from their home but take different times to reach the school although they follow the same route. Table 7.5 shows the distance travelled by them in different times. Study the table and explain the difference in their motions.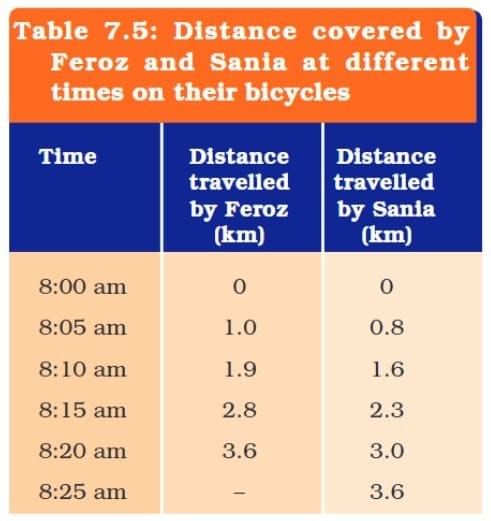
Plot the distance-time graph for their motions on the same scale and interpret.
Ans: From the table we observe:
- Both start at the same time (8:00 am) from the same place.
- Feroz reaches the school (3.6 km away) at 8:20 am.
- Sania reaches the school (3.6 km away) at 8:25 am.
This shows that:
Feroz cycles faster than Sania as he covers the same distance in less time.
Both cover equal distances in equal intervals of time, so their motion is uniform.
The difference lies in their speeds: Feroz’s average speed =
3.6 / 20 = 0.18 km/min3.6 / 25 = 0.144 km/min
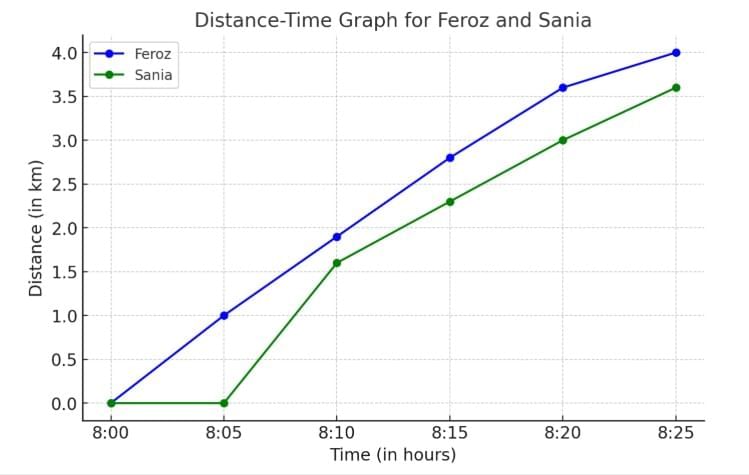
Conclusion: Both have uniform motion, but Feroz has a greater speed than Sania, so he reaches the school earlier.
Activity 7.11
Q: Take a piece of thread and tie a small piece of stone at one of its ends. Move the stone to describe a circular path with constant speed by holding the thread at the other end, as shown in Fig. 7.9.
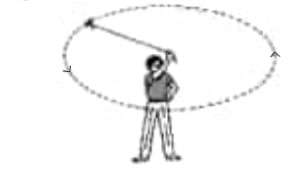 Fig 7.9: A stone describing a circular path with a velocity of constant magnitudeNow, let the stone go by releasing the thread. Can you tell the direction in which the stone moves after it is released?
Fig 7.9: A stone describing a circular path with a velocity of constant magnitudeNow, let the stone go by releasing the thread. Can you tell the direction in which the stone moves after it is released?
By repeating the activity for a few times and releasing the stone at different positions of the circular path, check whether the direction in which the stone moves remains the same or not.
Ans: When the stone is released, it moves tangentially to the circular path at the point of release. The direction of motion will not remain the same every time because the tangential direction changes at each point of release. Therefore, the direction of motion varies depending on the position at which the stone is released.
|
84 videos|478 docs|60 tests
|
FAQs on NCERT Solutions for Class 9 Science Chapter 7 - Motion
| 1. What is the difference between speed and velocity ? |  |
| 2. How do you calculate the average speed of an object ? |  |
| 3. What are the laws of motion proposed by Newton ? |  |
| 4. What is uniform motion and non-uniform motion ? |  |
| 5. How does acceleration relate to motion ? |  |