NCERT Solutions for Class 9 Maths Chapter 1 - Number System (Exercise 1.2)
Q1. State whether the following statements are true or false. Justify your answers.
(i) Every irrational number is a real number.
Ans: True
Reason: Irrational Numbers – A number is said to be irrational, if it cannot be written in the p/q, where p and q are integers and q ≠ 0.
i.e., Irrational numbers = π, e, √3, 5+√2, 6.23146…. , 0.101001001000….
Real numbers – The collection of both rational and irrational numbers are known as real numbers.
i.e., Real numbers = √2, √5, 56 , 0.102…
Every irrational number is a real number, however, every real number is not an irrational number.
(ii) Every point on the number line is of the form √m where m is a natural number.
Ans: False
Reason: The statement is false because as per the rule, a negative number cannot be expressed as square roots.
E.g., √9 =3 is a natural number.
But √2 = 1.414 is not a natural number.
Similarly, we know that negative numbers exist on the number line, but their square roots are not real numbers; they are complex.
E.g., √-7 = 7i, where i = √-1
The statement that every point on the number line is of the form √m, where m is a natural number is false.
(iii) Every real number is an irrational number.
Ans: False
Reason: The statement is false, the real numbers include both irrational and rational numbers. Therefore, every real number cannot be an irrational number.
Real numbers – The collection of both rational and irrational numbers are known as real numbers.
i.e., Real numbers = √2, √5, , 0.102…
Irrational Numbers – A number is said to be irrational if it cannot be written in the p/q, where p and q are integers and q ≠ 0.
i.e., Irrational numbers = π, e, √3, 5+√2, 6.23146…. , 0.101001001000….
Every irrational number is a real number, however, every real number is not irrational.
Q2. Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number.
Ans: No, the square roots of all positive integers are not irrational.
For example,
√4 = 2 is rational.
√9 = 3 is rational.
Hence, the square roots of positive integers 4 and 9 are not irrational. ( 2 and 3, respectively).
Q3. Show how √5 can be represented on the number line.
Ans:
Step 1: Let line AB be of 2 unit on a number line.
Step 2: At B, draw a perpendicular line BC of length 1 unit.
Step 3: Join CA
Step 4: Now, ABC is a right angled triangle. Applying Pythagoras theorem,
AB2 + BC2 = CA2
22 + 12 = CA2 = 5
⇒ CA = √5 . Thus, CA is a line of length √5 unit.
Step 5: Taking CA as a radius and A as a center draw an arc touching the number line. The point at which number line get intersected by arc is at √5 distance from 0 because it is a radius of the circle whose center was A.
Thus, √5 is represented on the number line as shown in the figure.
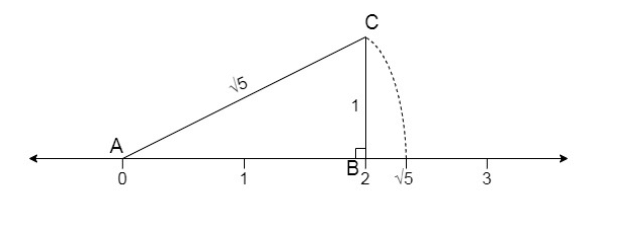 √5 on number line
√5 on number line
Q4. Classroom activity (Constructing the ‘square root spiral’) : Take a large sheet of paper and construct the ‘square root spiral’ in the following fashion. Start with a point O and draw a line segment OP1 of unit length. Draw a line segment P1 P2 perpendicular to OP1 of unit length (see Fig. 1.9). Now draw a line segment P2 P3 perpendicular to OP2 . Then draw a line segment P3 P4 perpendicular to OP3.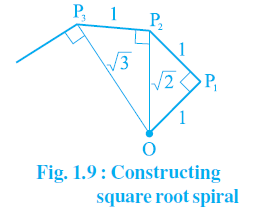 Continuing in this manner, you can get the line segment Pn–1Pn by drawing a line segment of unit length perpendicular to OPn–1. In this manner, you will have created the points P2 , P3 ,...., Pn ,... ., and joined them to create a beautiful spiral depicting √2, √3, √4, ....
Continuing in this manner, you can get the line segment Pn–1Pn by drawing a line segment of unit length perpendicular to OPn–1. In this manner, you will have created the points P2 , P3 ,...., Pn ,... ., and joined them to create a beautiful spiral depicting √2, √3, √4, ....
Ans: 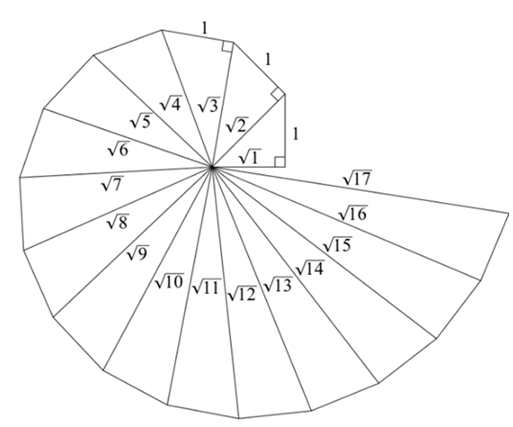 Step 1: Mark a point O on the paper. Here, O will be the center of the square root spiral.
Step 1: Mark a point O on the paper. Here, O will be the center of the square root spiral.
Step 2: From O, draw a straight line, OA, of 1cm horizontally.
Step 3: From A, draw a perpendicular line, AB, of 1 cm.
Step 4: Join OB. Here, OB will be of √2
Step 5: Now, from B, draw a perpendicular line of 1 cm and mark the end point C.
Step 6: Join OC. Here, OC will be of √3
Step 7: Repeat the steps to draw √4, √5, √6….
|
40 videos|471 docs|57 tests
|
FAQs on NCERT Solutions for Class 9 Maths Chapter 1 - Number System (Exercise 1.2)
| 1. What are the different types of numbers in the number system? |  |
| 2. How do you convert a decimal number to a fraction? |  |
| 3. What is the significance of the number line in the number system? |  |
| 4. How to determine if a number is rational or irrational? |  |
| 5. What are the properties of rational numbers? |  |






















